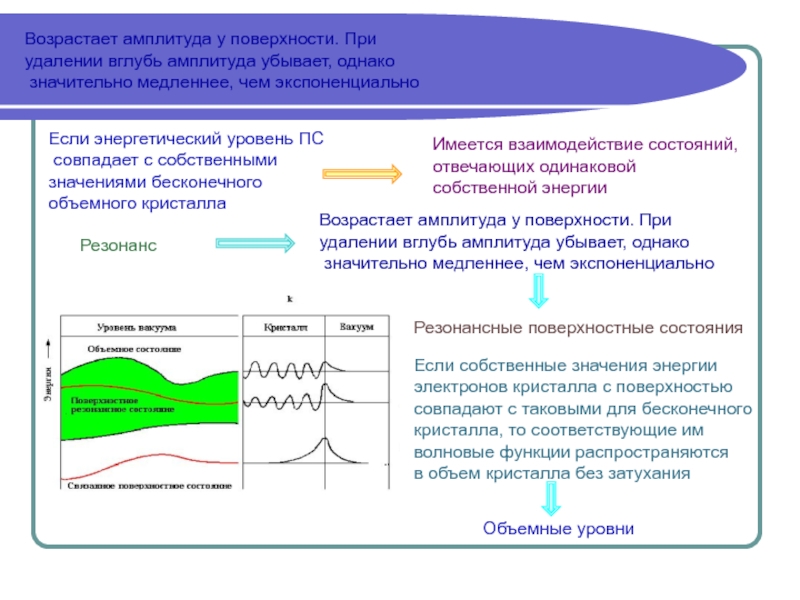
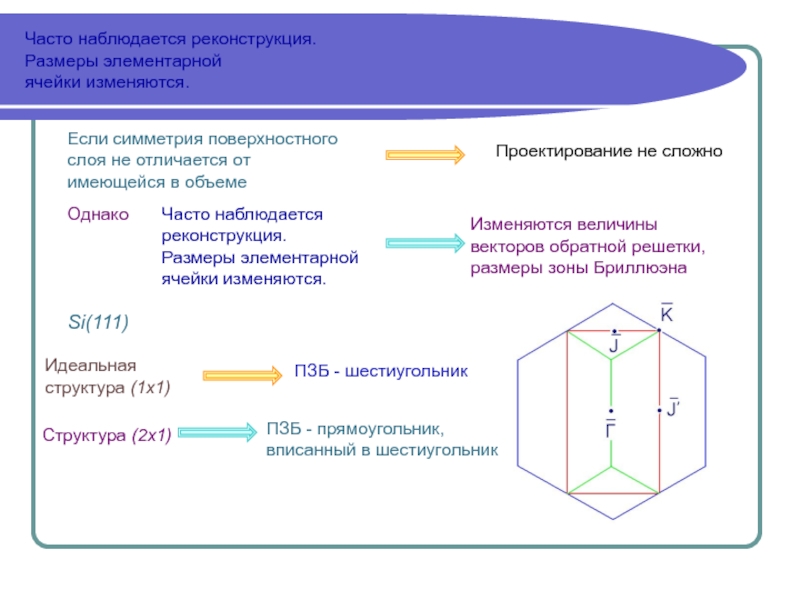
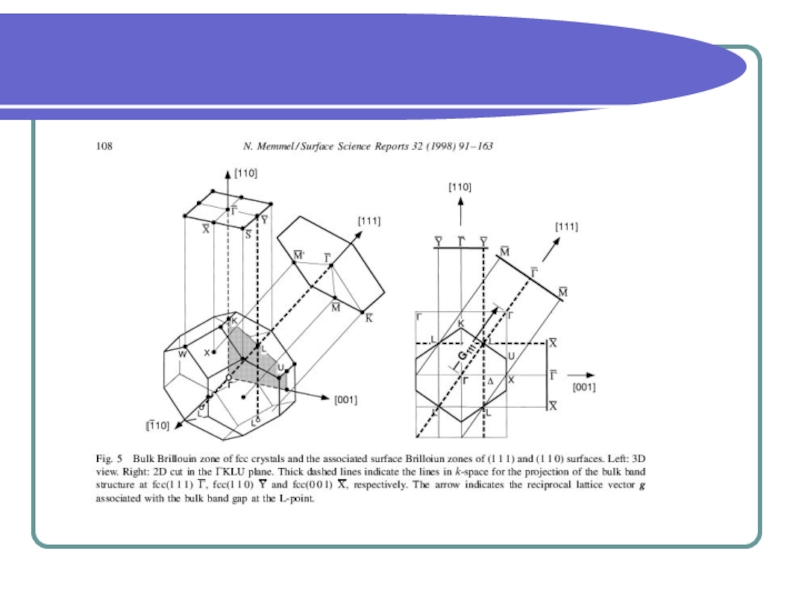
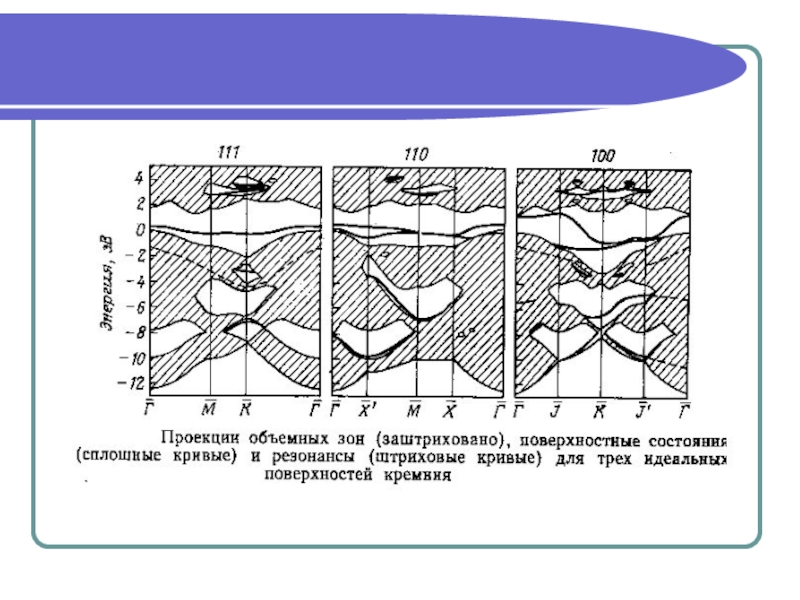
uk(r) инвариантна относительно трансляции
на любой
вектор решетки Ri:uk(r) = uk(r+Ri)
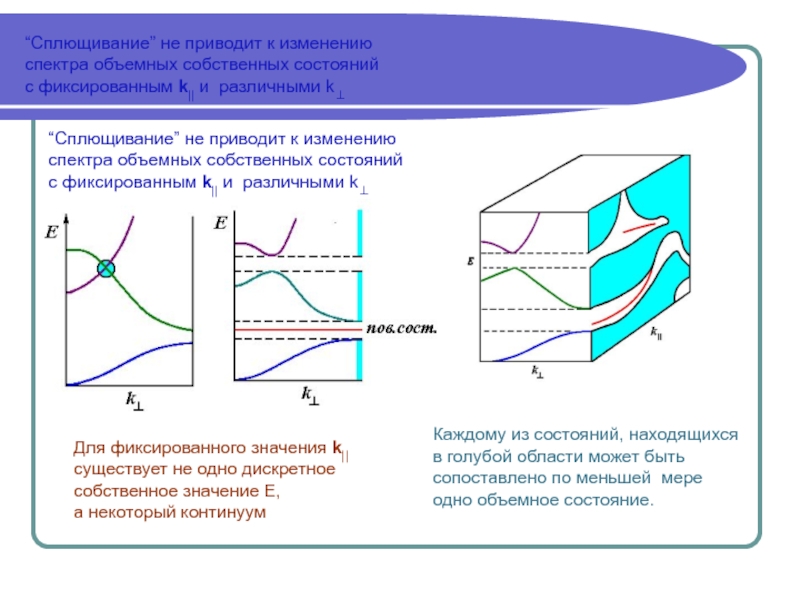
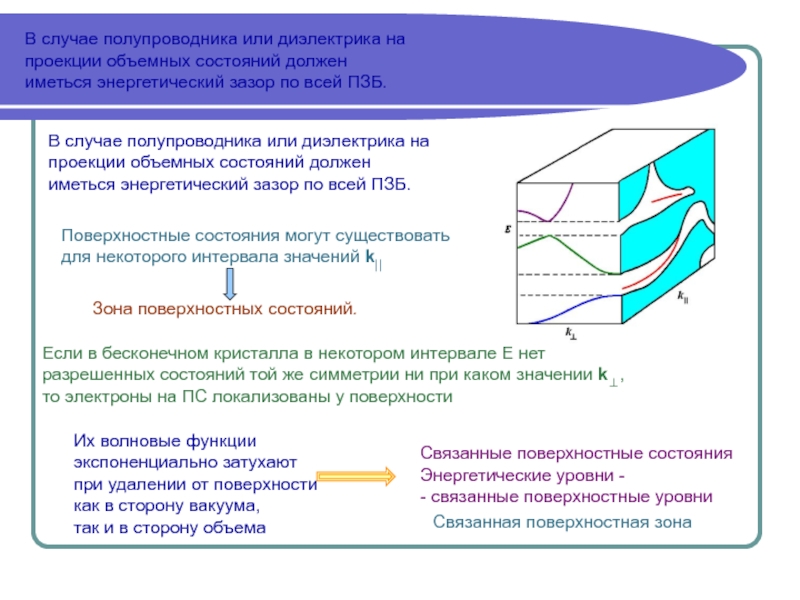
Дисперсионные зависимости ε(k)
Анализ ε(k) проводят используя понятие зоны Бриллюэна
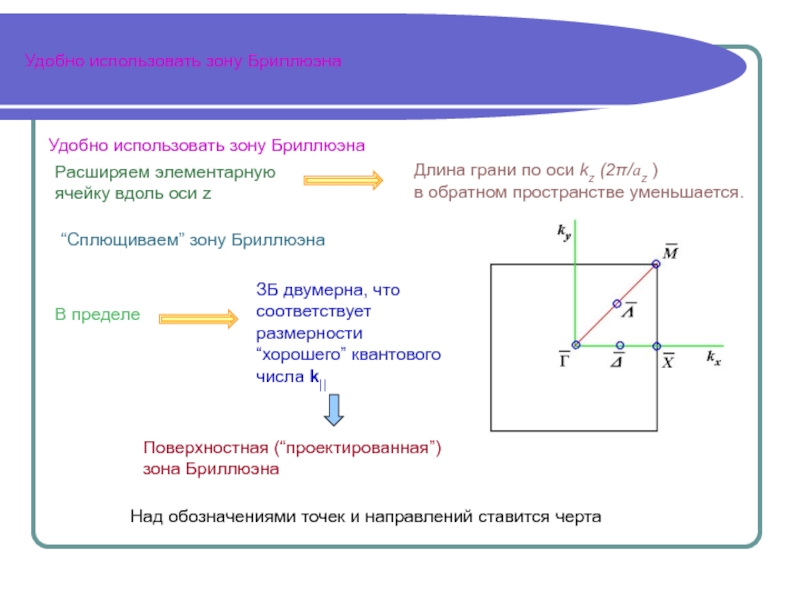
Зона Бриллюэна
Для объема
Функции Блоха
k - трехмерный волновой вектор
Ячейка Вигнера-Зейтца в пространстве импульсов
Физические величины
Периодические функции
по k,период равен
вектору обратной решетки G
Состояния с
k и k’=k+G
физически
эквивалентны
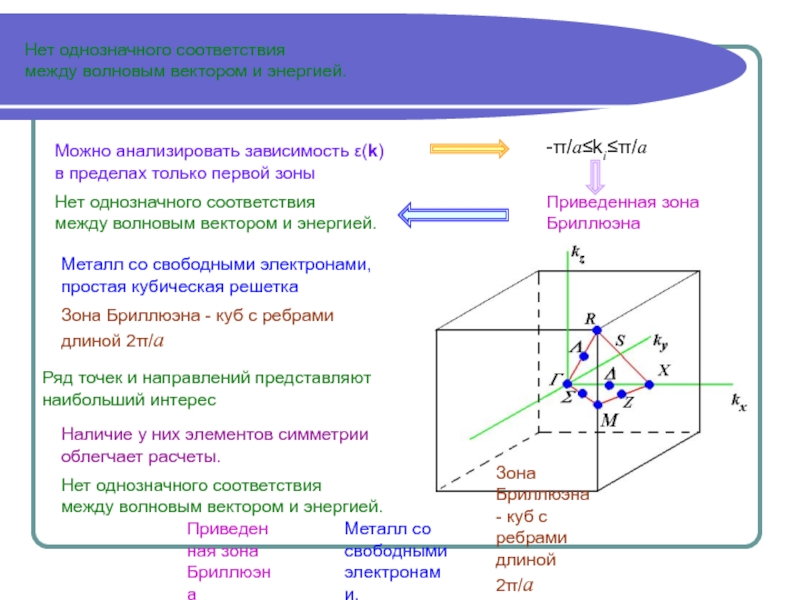
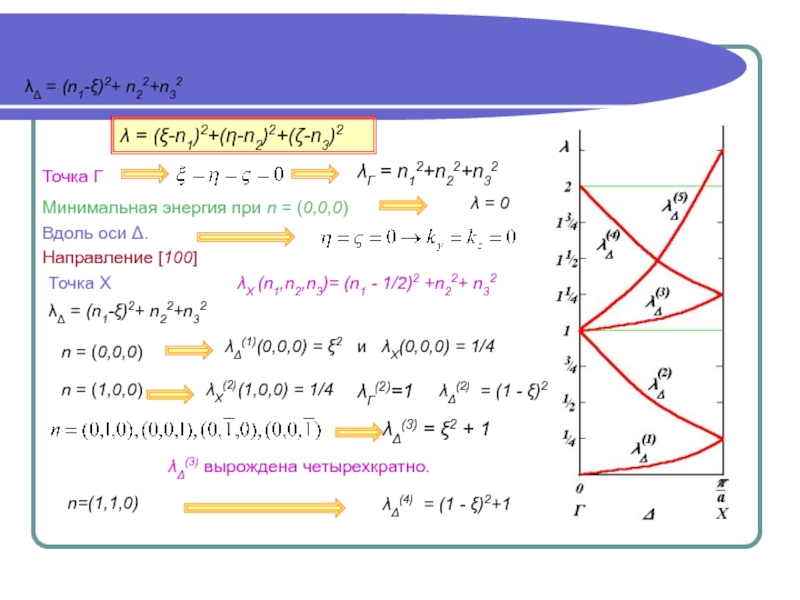
![Поверхностная (проектированная) зона Бриллюэна ε(k) при изменении k вдоль направления [001] (Δ) от точки Г ε(k) при изменении k вдоль направления [001] (Δ) от точки Г до Х. ε(k) при изменении k](/img/thumbs/ff94b21e242cfe7e6b1704ab2c7fd42a-800x.jpg)