Правильные многогранники

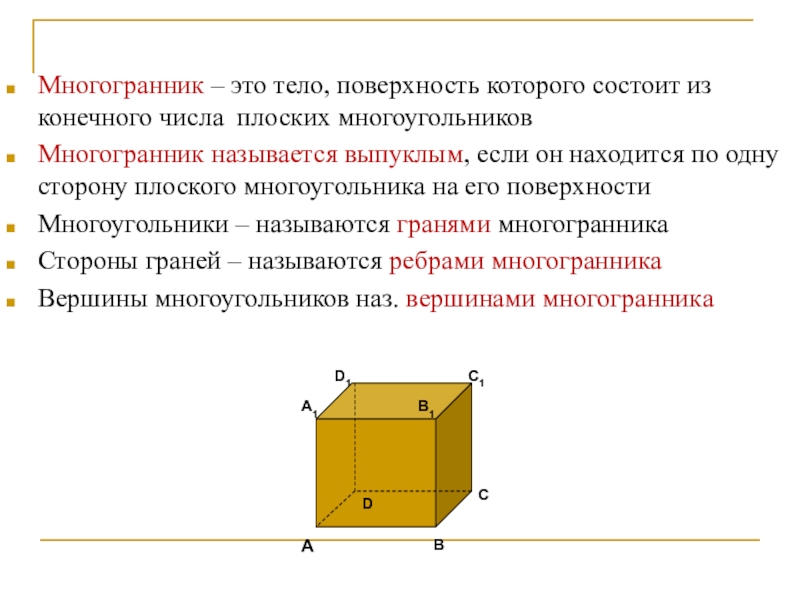
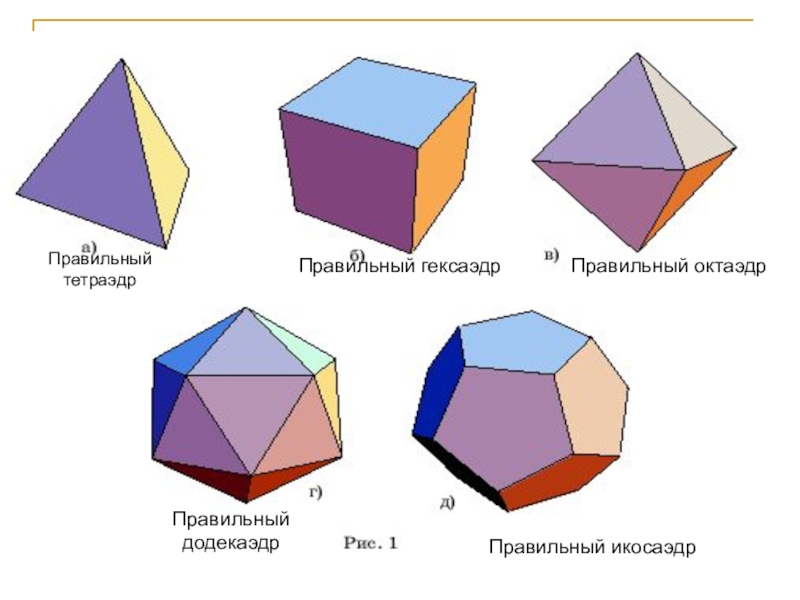
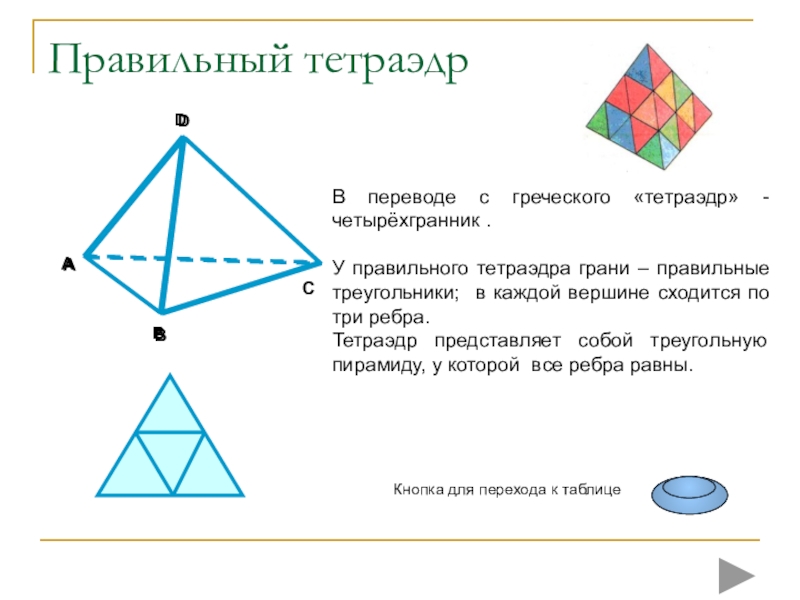
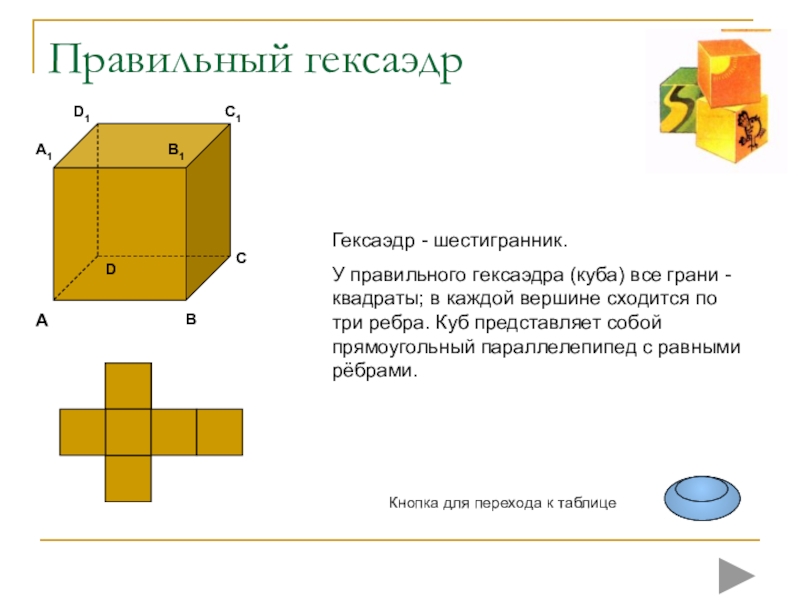
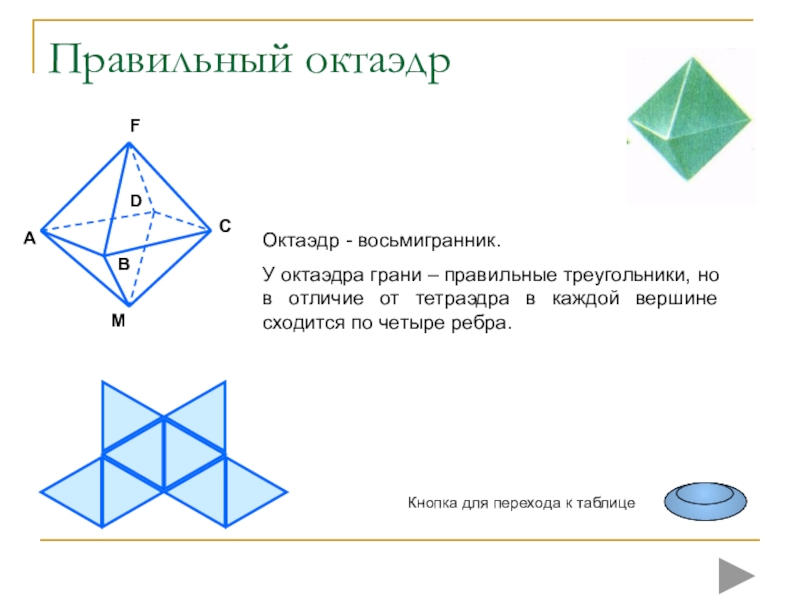
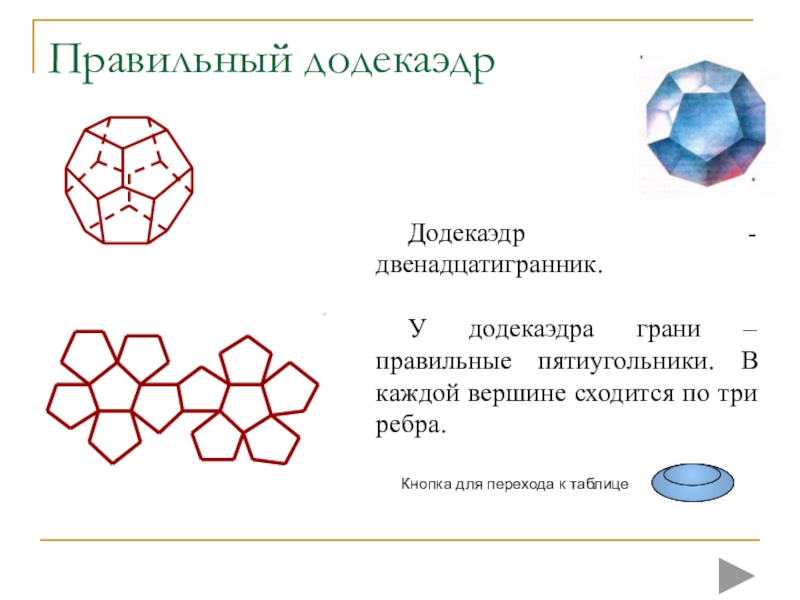
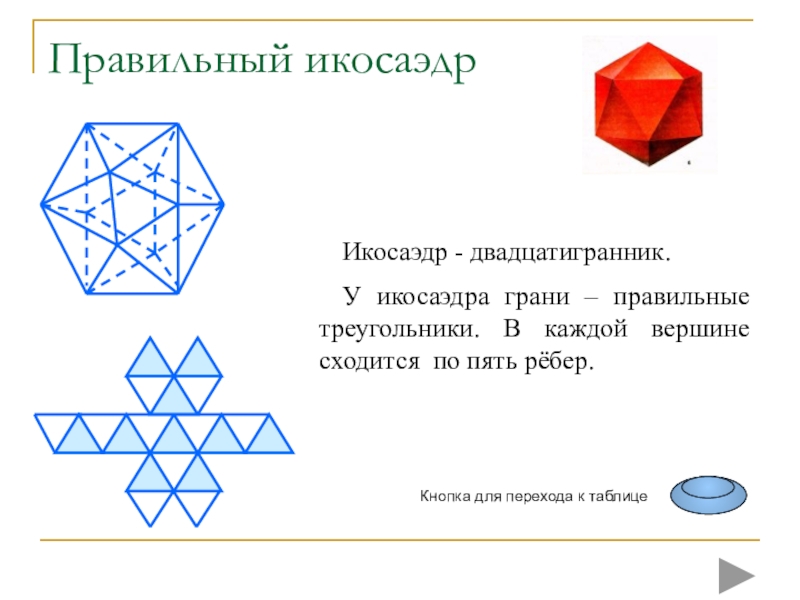
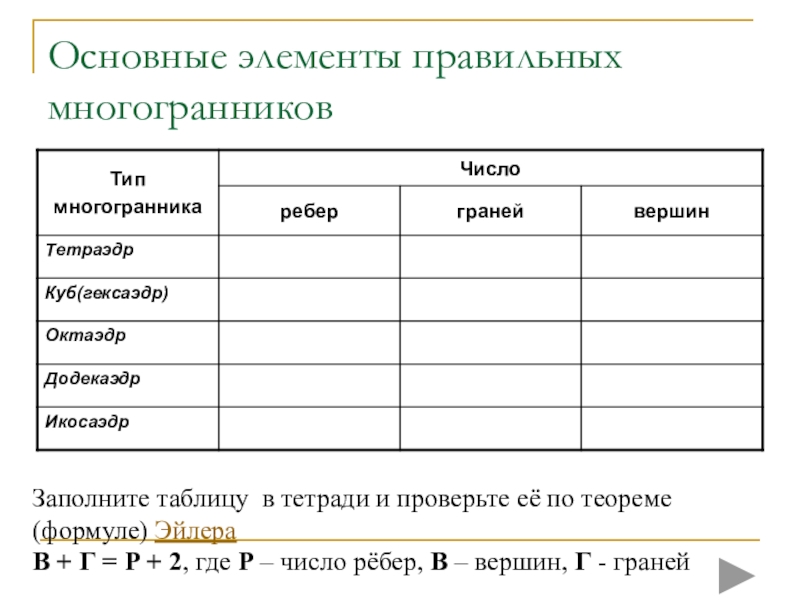
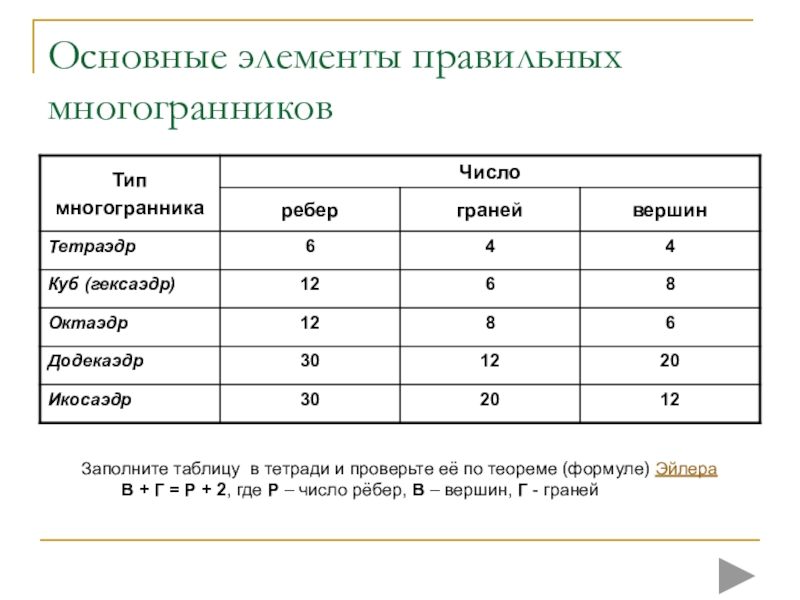
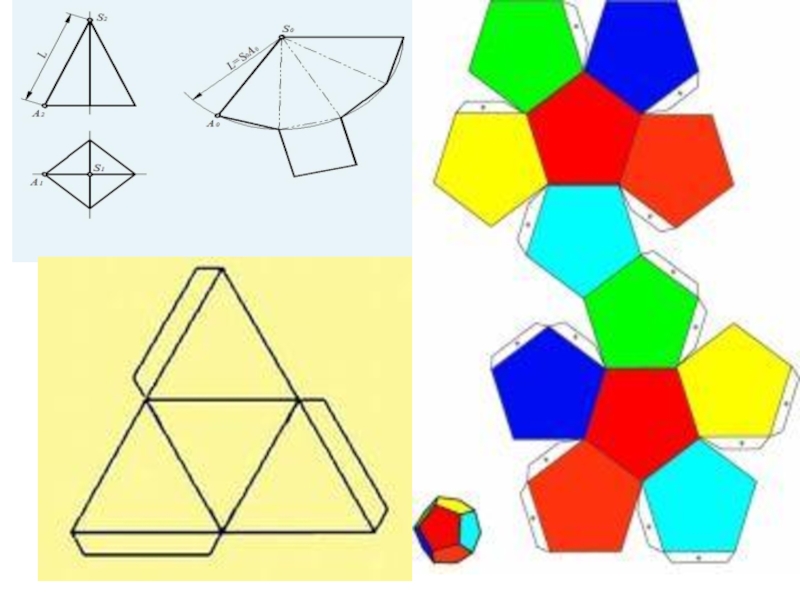
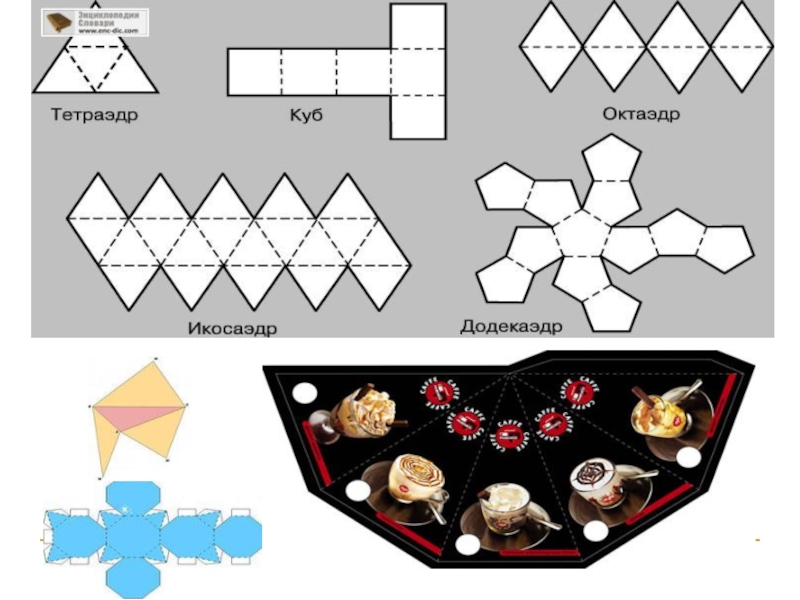
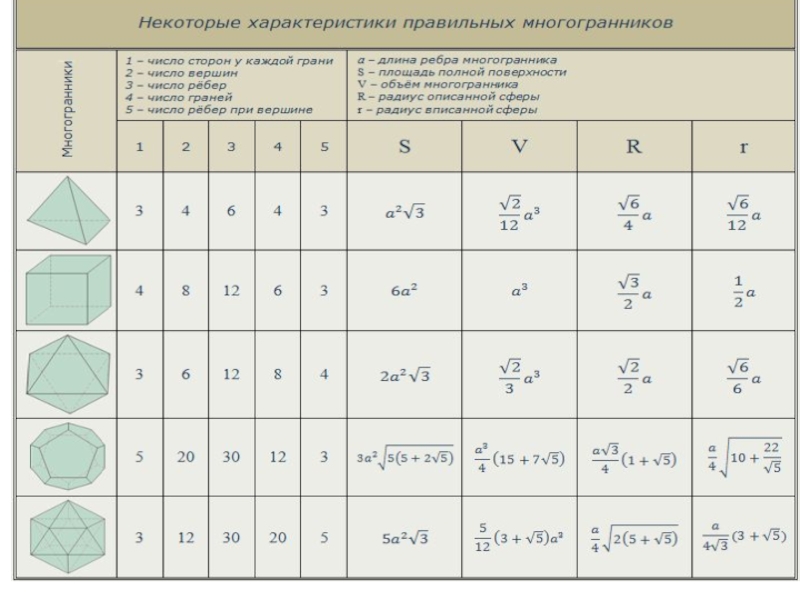
плоских многоугольников
Многогранник называется выпуклым, если он находится по одну

сторону плоского многоугольника на его поверхности
Многоугольники – называются гранями многогранника
Стороны граней – называются ребрами многогранника
Вершины многоугольников наз. вершинами многогранника

правильными многоугольниками с одним и тем же числом сторон и

в каждой вершине многогранника сходится одно и то же число ребер

Правильный икосаэдр

Правильный икосаэдр

.

У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра.
Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.

Кнопка для перехода к таблице

в каждой вершине сходится по три ребра. Куб представляет собой

прямоугольный параллелепипед с равными рёбрами.

Кнопка для перехода к таблице

в отличие от тетраэдра в каждой вершине сходится по четыре

ребра.

Кнопка для перехода к таблице

каждой вершине сходится по три ребра.
Кнопка для перехода к таблице

каждой вершине сходится по пять рёбер.
Кнопка для перехода к таблице

в Древней Греции. Великий древнегреческий мыслитель Платон считал, что четыре

из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа») или «пятая сущность».
Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков

по теореме (формуле) Эйлера
В + Г = Р + 2,

где Р – число рёбер, В – вершин, Г - граней

по теореме (формуле) Эйлера
В + Г = Р + 2,

где Р – число рёбер, В – вершин, Г - граней

как многие кристаллы имеют форму правильных многогранников.
Например, куб - монокристалл

поваренной соли (NaCl), октаэдр - монокристалл алюмокалиевых квасцов, одна из форм кристаллов алмаза - октаэдр

Кристаллы бывают самой различной формы: 1 — берилл, 2 — аметист, 3 — рубин, 4 — кристалл металла германия — денорит, 5 — горный хрусталь, 6 — испанский шпат, 7 — поваренная соль, 8 — ограненный алмаз—бриллиант, вправленный в кольцо.
В колбе с перенасыщенным раствором на конце проволочки, опущенной в раствор, растет кристалл поваренной соли.

организма феодарии представляет собой икосаэдр.
Минерал сильвин также имеет кристаллическую

решетку в форме куба.

Молекулы воды имеют форму тетраэдра.

Минерал куприт образует кристаллы в форме октаэдров.

Кристаллы пирита имеют форму додекаэдра

правильной призмы все боковые грани – равные прямоугольники.

о существовании пяти типов правильных многогранников.
Заполните в тетради таблицу «Элементы

правильных многогранников.
Решите задачи №56 (с.247),№35(с.245)

Академии Наук, автор огромного количества глубоких результатов во всех областях

математики. Полное собрание сочинений Эйлера-72 тома-не вышло целиком и до сих пор. По единодушному признанию современников Леонард Эйлер - первый математик мира. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку — топологию.
Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В + Г = Р + 2

«Эйлер не проглядел ничего в современной ему математике, хотя последние семнадцать лет своей жизни был совершенно слеп».
Э.Т.Белл

воспользуйся кнопкой