Правильный многогранник

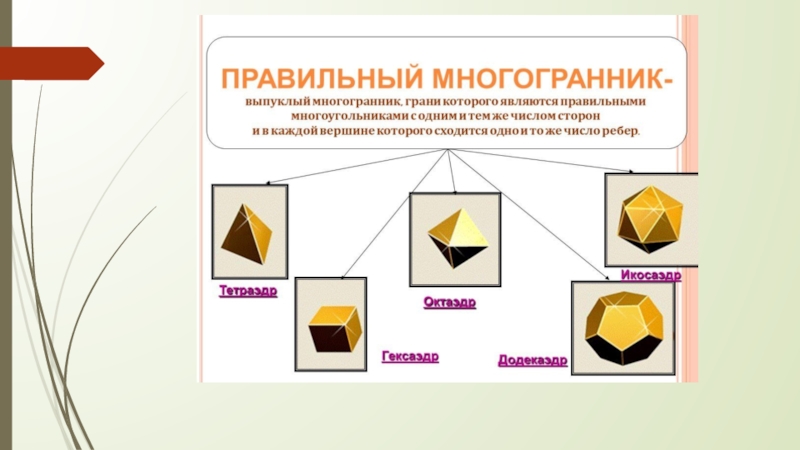
пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти

правильных многоугольников (рис. 1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.

а

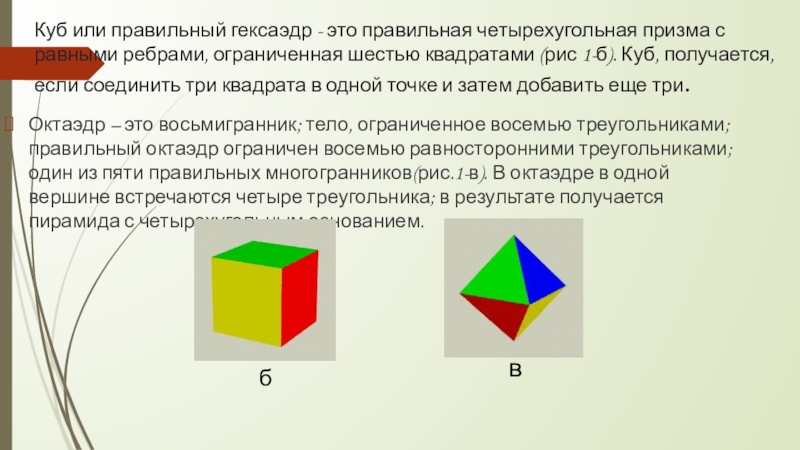
* Платоновы тела: (а) октаэдр («Огонь»), (б) гексаэдр или куб («Земля»),
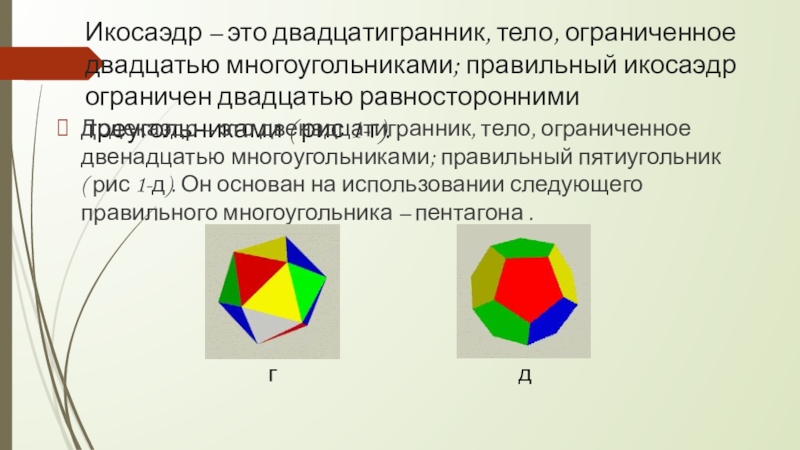
(в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр («Вселенский разум»).

равными ребрами, ограниченная шестью квадратами (рис 1-б). Куб, получается, если

соединить три квадрата в одной точке и затем добавить еще три.

Октаэдр – это восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников(рис.1-в). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием.

б

в

ограничен двадцатью равносторонними треугольниками ( рис 1-г).
Додекаэдр – это двенадцатигранник,

тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник ( рис 1-д). Он основан на использовании следующего правильного многоугольника – пентагона .

г

д

углы, содержащие две грани с общим ребром, равны.

правильного тетраэдра является прямая, проходящая через середину двух противоположных ребер.

То есть правильный тетраэдр имеет три оси симметрии.
Плоскостью симметрии правильного тетраэдра будет плоскость, проходящая через ребро, перпендикулярно к противоположному ребру. То есть правильный тетраэдр имеет шесть плоскостей симметрии.

прямые, которые проходят через центры противоположных граней или середины противоположных

ребер. Поскольку грани гексаэдра – квадраты, значит, оси симметрии будут проходить через точки пересечения диагоналей противоположных граней. То есть у куба девять осей симметрии. Все оси симметрии проходят через центр симметрии.

Проводя через каждые две оси симметрии плоскость, мы получим плоскость симметрии куба. То есть у куба девять плоскостей симметрии.

вершины октаэдра и прямые, которые проходят через середины противоположных ребер.

То есть у октаэдра девять осей симметрии.

Точка пересечения осей симметрии октаэдра будет центром симметрии.
Плоскостями симметрии октаэдра будут плоскости, которые проходят через каждые четыре вершины октаэдра. Таких плоскостей три. И плоскости, которые проходят через две вершины, не лежащие в одной грани, и середины противоположных ребер. Таких плоскостей шесть. То есть у правильного октаэдра девять плоскостей симметрии.

ребер. Их пятнадцать. То есть у правильного додекаэдра пятнадцать осей

симметрии.

Центром симметрии правильного додекаэдра будет точка пересечения всех осей симметрии.
Плоскости, проходящие в каждой грани через вершину и середину противолежащего ребра будут плоскостями симметрии.

Таких плоскостей пятнадцать. То есть у правильного додекаэдра пятнадцать плоскостей симметрии.

противолежащих параллельных ребер. Таких прямых пятнадцать. То есть у правильного

икосаэдра пятнадцать осей симметрии.

Центром симметрии правильного икосаэдра является точка пересечения всех осей симметрии.
Плоскости симметрии правильного икосаэдра проходят через четыре вершины, которые лежат в одной плоскости, и середины противоположных ребер. Таких плоскостей пятнадцать. То есть у правильного икосаэдра пятнадцать плоскостей симметрии.