Слайд 1Предельные величины, эластичности
Функция спроса на некоторый товар
Q(P)=-2P+12 при P
Q(P)=0 при P>6.
Построить график функции (Excel)
Составить функцию дохода R(P)
Построить
график функции дохода (Excel)
Определить по графику точку максимума и вычислить эту точку аналитически
(с помощью производной)
5) Найти функцию предельного дохода MR(P). Найти предельный доход при цене
2 ден.ед., 5 ден.ед, 3 ден.ед. Дать интерпретацию.
6) Построить график функции предельного дохода MR(P)
7) Определить по графику точку в которой предельный доход равен 0. Что вы заметили?
8) Вычислить эластичность спроса по цене при цене равной 2 ден.ед., 5 ден.ед, 3 ден.ед.
Дайте интерпретацию
9) Постройте график функции эластичности, определите на этом графике участки
эластичного и неэластичного спроса.
Слайд 2Предельный доход (предельная выручка).
Пусть Q – объем произведенной продукции.
R(Q) – доход от ее реализации.
называется предельным доходом.
Слайд 3 то
Если
если
мало.
Предельный доход показывает дополнитель-
ный доход от
реализации дополнительной
единицы продукции.
Предельный доход (предельная выручка).
Слайд 4Эластичность в экономике.
Эластичность показывает на сколько процентов изменится функция при
изменении аргумента на 1%.
Слайд 5Эластичность в экономике.
Пусть Q(P) – функция спроса от цены.
-
показывает на сколько процентов изменится спрос при увеличении цены на
1%.
- эластичность спроса по цене.
Слайд 6Эластичность в экономике.
Если
то спрос называют эластичным.
Если
то спрос называют неэластичным.
Если
то спрос
называют спросом с единичной
эластичностью.
Если
то спрос называют совершенно неэлас-
тичным.
Слайд 7Соотношение эластичности спроса и предельного дохода.
Пусть Q(P) – функция спроса
на некоторый товар;
R(P)=P·Q(P) – функция дохода от реализации товара;
-
предельный доход.
или
?
Слайд 8Соотношение эластичности спроса и предельного дохода.
Если
т.е. спрос эластичен,
то
т.е. увеличение цены приведет
к уменьшению дохода.
Слайд 9Соотношение эластичности спроса и предельного дохода.
Если
т.е. спрос неэластичен,
то
т.е. увеличение цены приведет
к увеличению дохода.
Слайд 10Соотношение эластичности спроса и предельного дохода.
Если
т.е. спрос с
единичной
т.е. увеличение
цены не изменит доход.
эластичностью, то
Слайд 11Соотношение эластичности спроса и предельного дохода.
Вывод: С возрастанием цены для
продукции с
эластичным спросом суммарный доход уменьша-
ется, а для товаров
неэластичного спроса увели-
чивается.
Слайд 12Работа № 1
Функция спроса на некоторый товар
Q(P)=-aP+b при P
Q(P)=0 при P>b/a, где a – последняя цифра
вашей зачетной книжки,
b=10*a.
Построить график функции (Excel)
Составить функцию дохода R(P)
Построить график функции дохода (Excel)
Определить по графику точку максимума и вычислить эту точку аналитически
(с помощью производной)
5) Найти функцию предельного дохода MR(P). Найти предельный доход при цене
P=2 ден.ед., 5 ден.ед, 8 ден.ед. Дать интерпретацию.
6) Построить график функции предельного дохода MR(P)
7) Определить по графику точку в которой предельный доход равен 0. Что вы заметили?
8) Вычислить эластичность спроса по цене при цене равной 2 ден.ед., 5 ден.ед, 8 ден.ед.
Дайте интерпретацию
9) Постройте график функции эластичности, определите на этом графике участки
эластичного и неэластичного спроса.
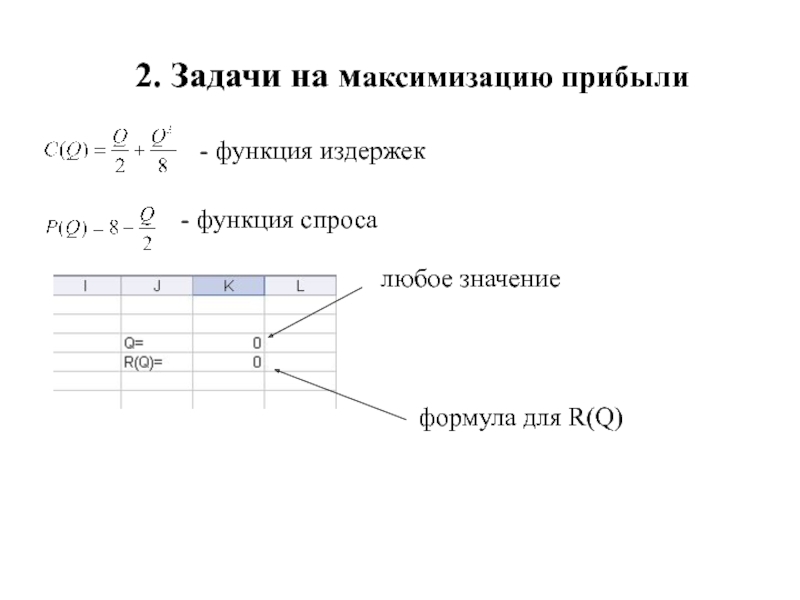
Слайд 132. Задачи на максимизацию прибыли
- функция издержек
- функция спроса
Составить функцию
прибыли П(Q)
Найти Q, при котором прибыль максимальна аналитически
(без компьютера).
3) Изобразить график функции П(Q) (Excel)
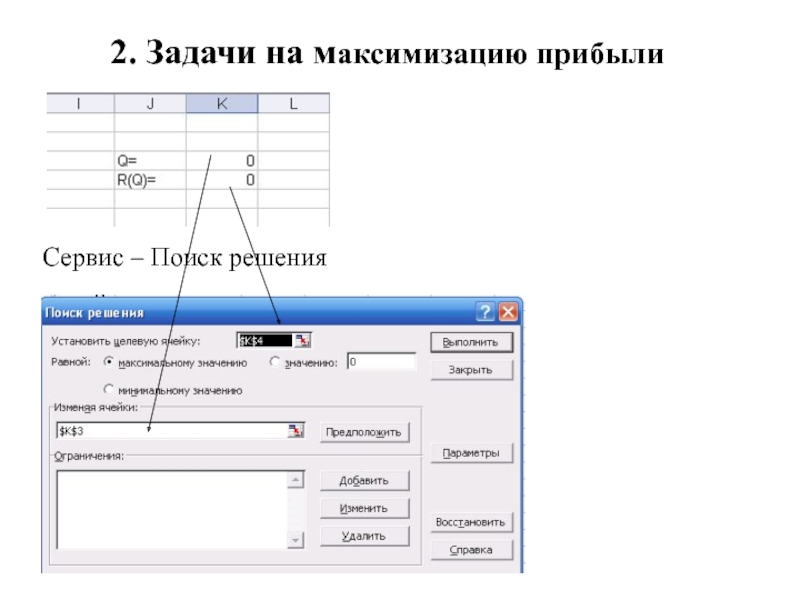
4) Найти Q, при котором прибыль максимальна с помощью
Excel
5) Сравните результат аналитического решения и решения Excel
Слайд 142. Задачи на максимизацию прибыли
- функция издержек
- функция спроса
любое значение
формула
для R(Q)
Слайд 152. Задачи на максимизацию прибыли
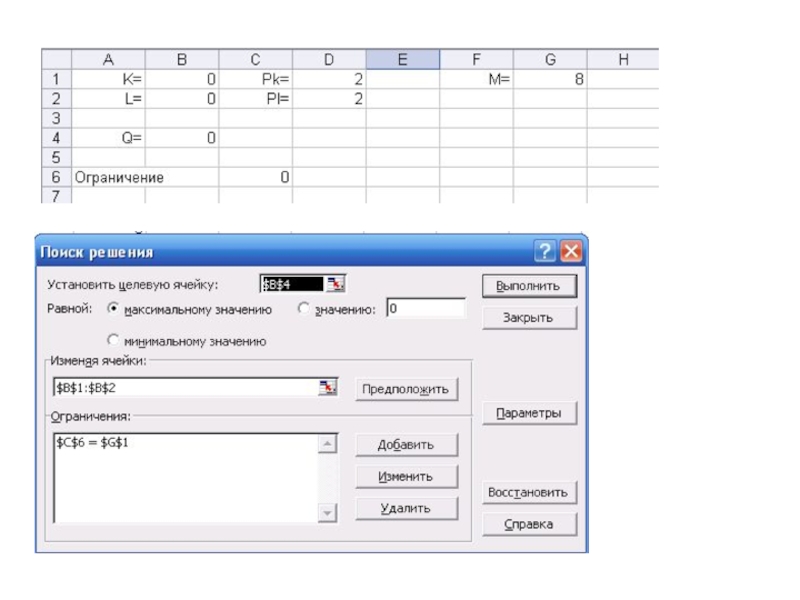
Сервис – Поиск решения
Слайд 162. Задачи на максимизацию прибыли
Слайд 172. Задачи на максимизацию прибыли
- функция издержек
- функция спроса
Составить функцию
прибыли П(Q)
Найти Q, при котором прибыль максимальна аналитически
(без компьютера).
3) Изобразить график функции П(Q) (Excel)
4) Найти Q, при котором прибыль максимальна с помощью
Excel
5) Сравните результат аналитического решения и решения Excel
Слайд 18Работа 2. Задачи на максимизацию прибыли
Вариант 1 4.181;
Вариант 2
4.182;
Вариант 3 4.184
Вариант 4 4.185
Вариант 5 4.186
Вариант 6 4.187
Вариант
7 4.188
Вариант 8 4.189
Вариант 10 4.190
Вариант 11 4.193
Вариант 12 4.194
Слайд 193. Задачи на максимизацию прибыли функций двух и более переменных
Пример
1 Фирма производит 2 товара и продает их
по ценам
8 и 10 д.е. Функция издержек
Составит функцию прибыли
Найти объемы производства, при которых
прибыль максимальна аналитически.
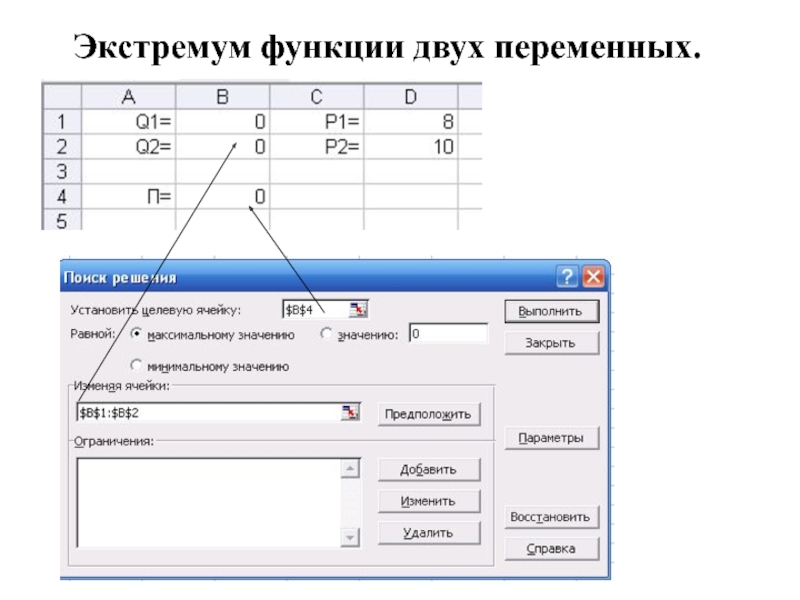
3) Найти объемы производства, при которых
прибыль максимальна с помощью Поиск решения
Excel.
Слайд 20Необходимое условие экстремума. Пусть
- точка
экстремума функции z=f(x,y). Тогда
то
- точка максимума
Если то - точка минимума
Если то не является точкой
экстремума
Экстремум функции двух переменных.
Достаточное условие экстремума. Пусть - крити-
ческая точка функции z=f(x,y).
Тогда
Слайд 22Экстремум функции двух переменных.
Пример 1 Фирма производит 2 товара и
продает их
по ценам 8 и 10 д.е. Функция издержек
формула для прибыли
Слайд 23Экстремум функции двух переменных.
Слайд 24Экстремум функции двух переменных.
Пример 1 Фирма производит 2 товара и
продает их
по ценам 8 и 10 д.е. Функция издержек
Слайд 25Работа 3. Задачи на максимизацию прибыли функций двух и более
переменных
Вариант 1 5.229
Вариант 2 5.230
Вариант 3 5.231
Вариант 4. 5.232
Вариант 5
5.229
Вариант 6 5.230
Вариант 7 5.231
Вариант 8. 5.232
Слайд 264. Экономические задачи на условный экстремум
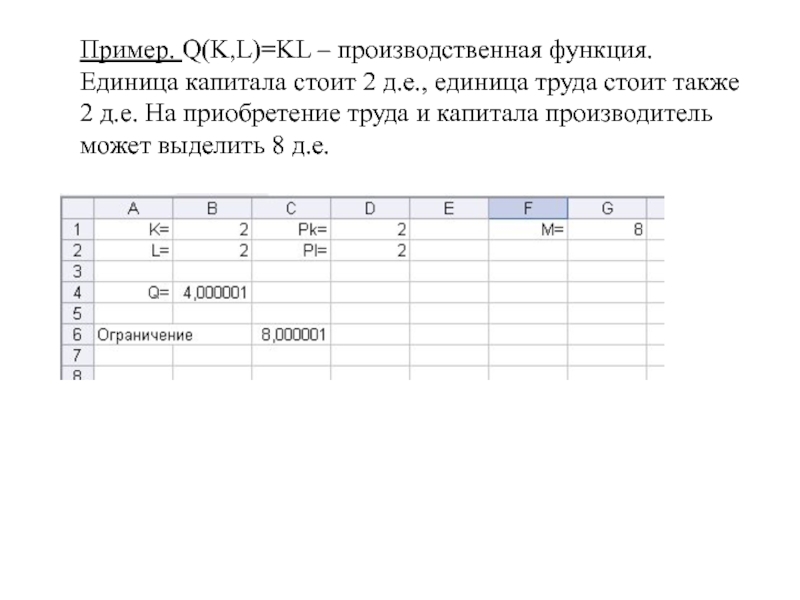
Пример. Q(K,L)=KL – производственная функция.
Единица
капитала стоит 2 д.е., единица труда стоит также 2
д.е. На приобретение труда и капитала производитель может выделить 8 д.е.
Найти затраты труда и капитала, при которых объем
выпуска максимален
решить задачу методом подстановки
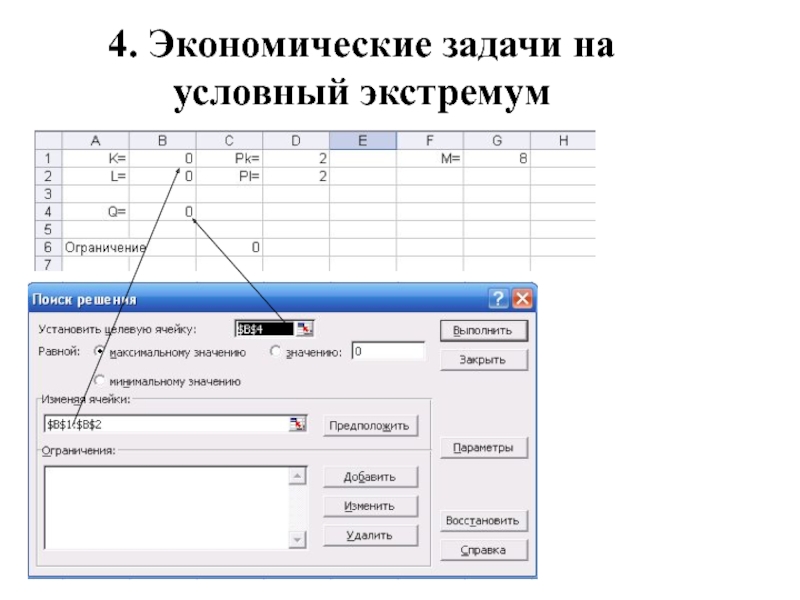
решить задачу с помощью Поиск решения в Excel.
Слайд 274. Экономические задачи на условный экстремум
Пример. Q(K,L)=KL – производственная функция.
Единица
капитала стоит 2 д.е., единица труда стоит также 2
д.е. На приобретение труда и капитала производитель может выделить 8 д.е.
=В1*В2 (K*L)
цены единиц капитала и труда
Общая сумма
=D1*B1+D2*B2 – расходы (K*PK+L*PL)
Слайд 284. Экономические задачи на условный экстремум
Слайд 294. Экономические задачи на условный экстремум
Слайд 31Пример. Q(K,L)=KL – производственная функция. Единица капитала стоит 2 д.е.,
единица труда стоит также 2 д.е. На приобретение труда и
капитала производитель может выделить 8 д.е.
Слайд 32Работа 4. Экономические задачи на условный экстремум
Вариант 1 5.233
Вариант 2
5.234
Вариант 3 5.235
Вариант 6 5.236
Вариант 7 5.237
Вариант 8 5.238