Разделы презентаций

Предмет и метод начертательной геометрии. Комплексный чертеж Лекция № 1

Содержание

План лекции

Слайды и текст этой презентации

Слайд 1Предмет и метод начертательной геометрии. Комплексный чертеж
Лекция № 1

Предмет и метод начертательной геометрии. Комплексный чертежЛекция № 1

Слайд 2План лекции

План лекции

Слайд 3Начертательная геометрия-
Раздел геометрии, в котором пространственные фигуры изучаются с помощью

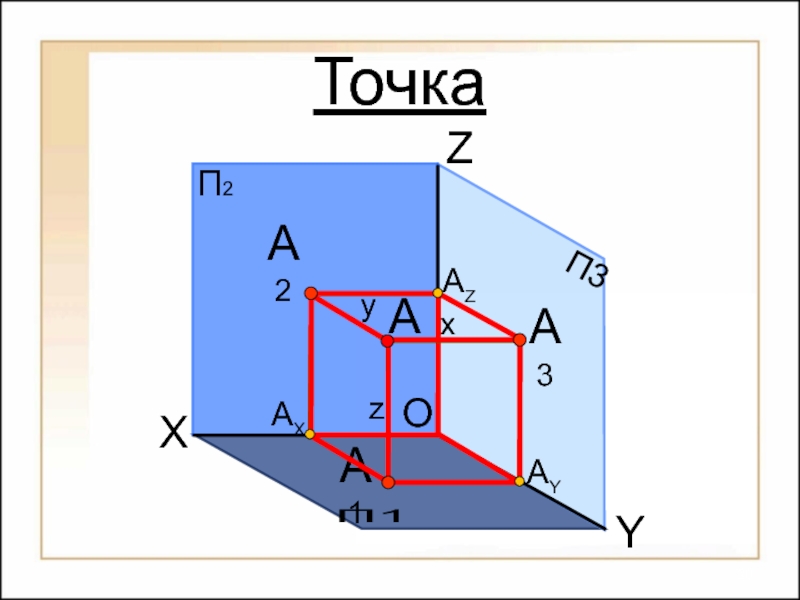
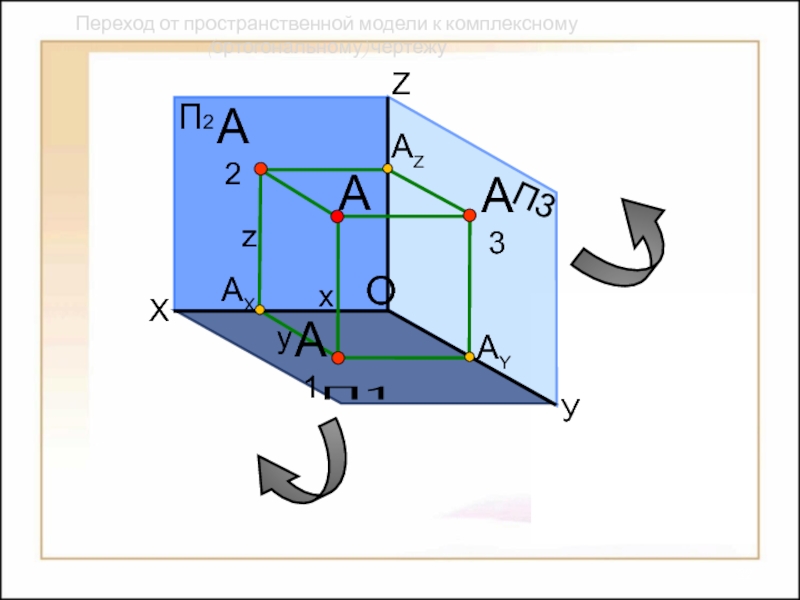
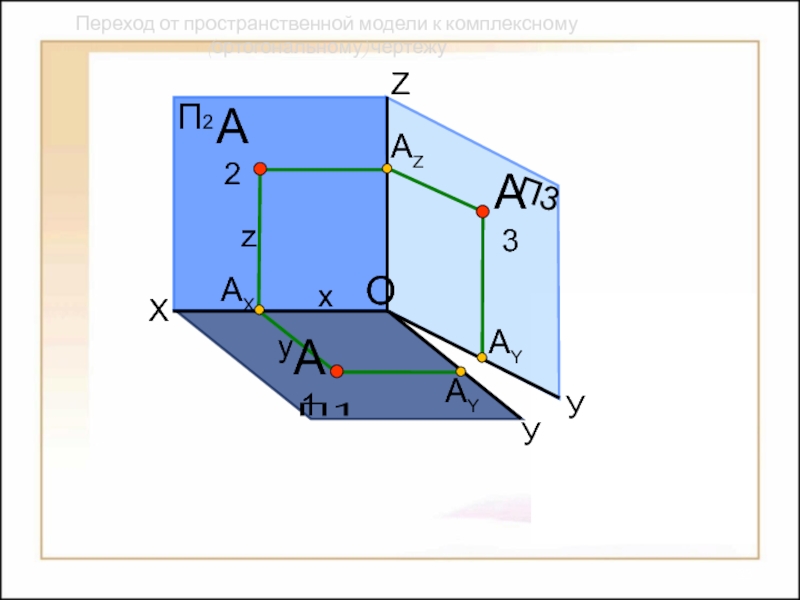
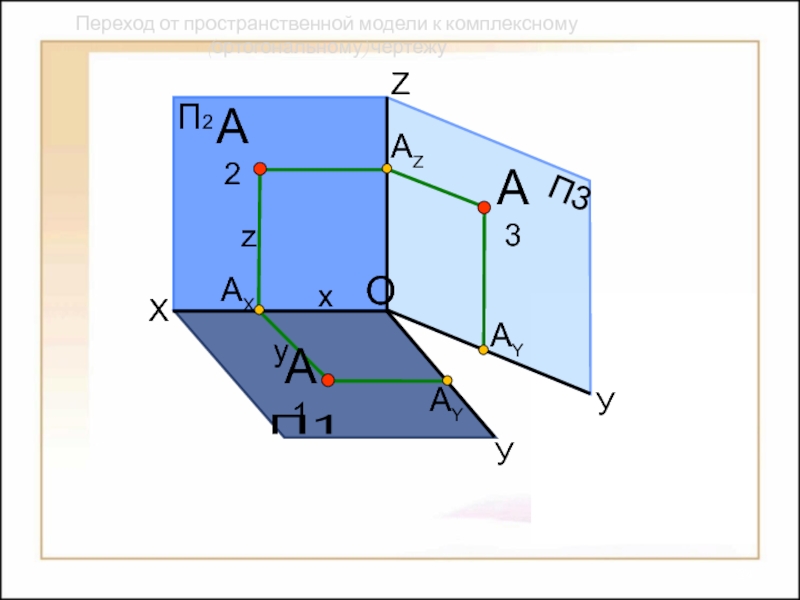
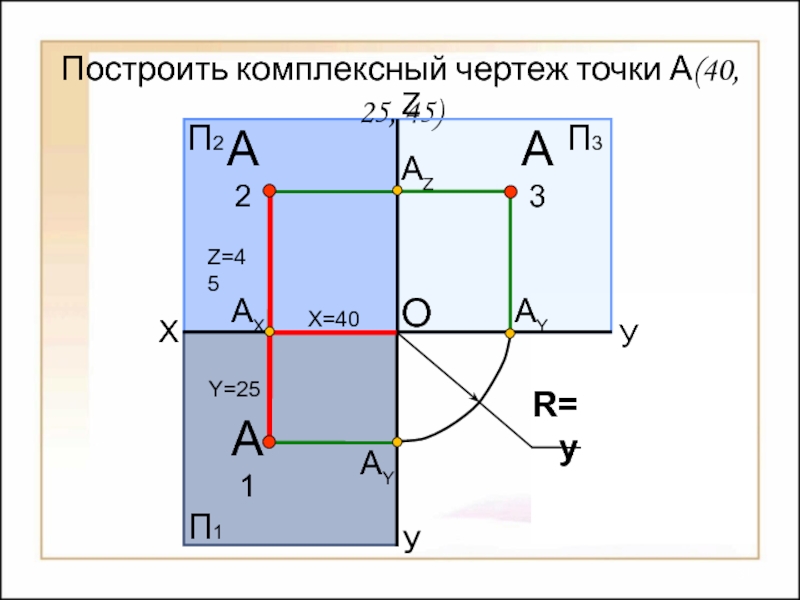
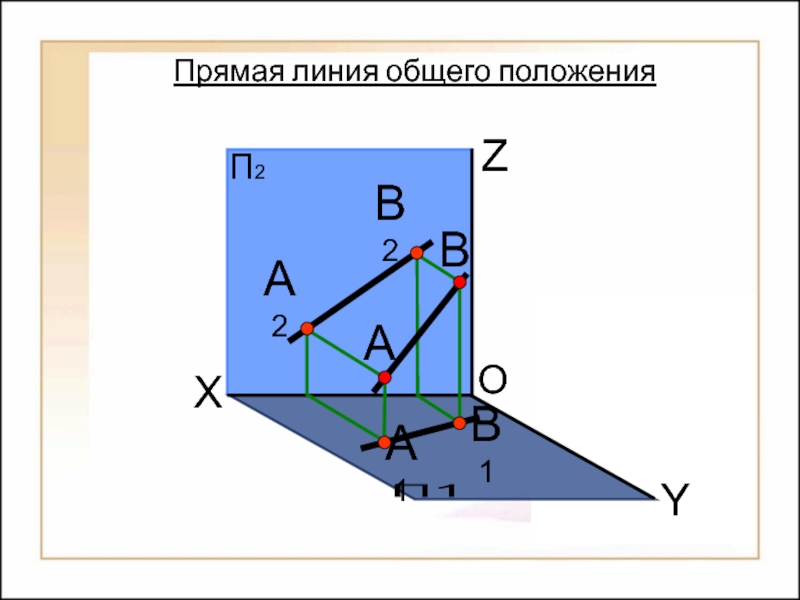
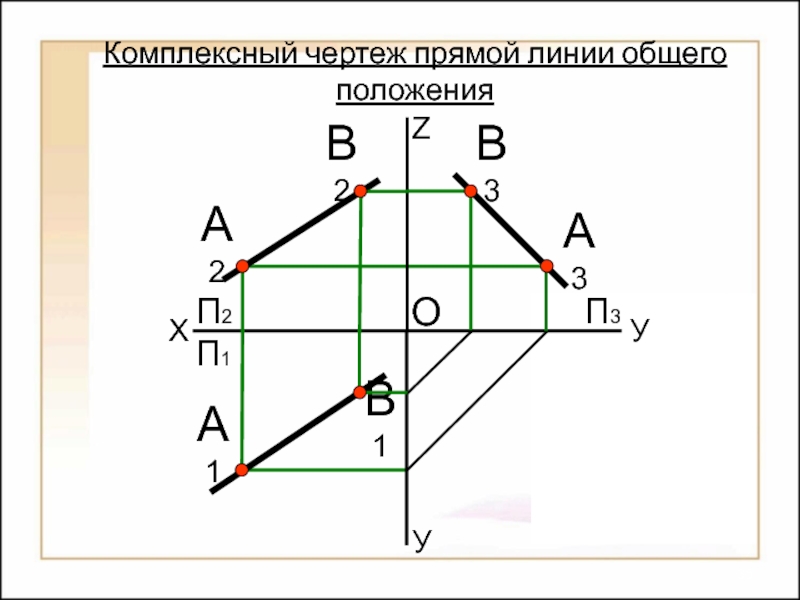
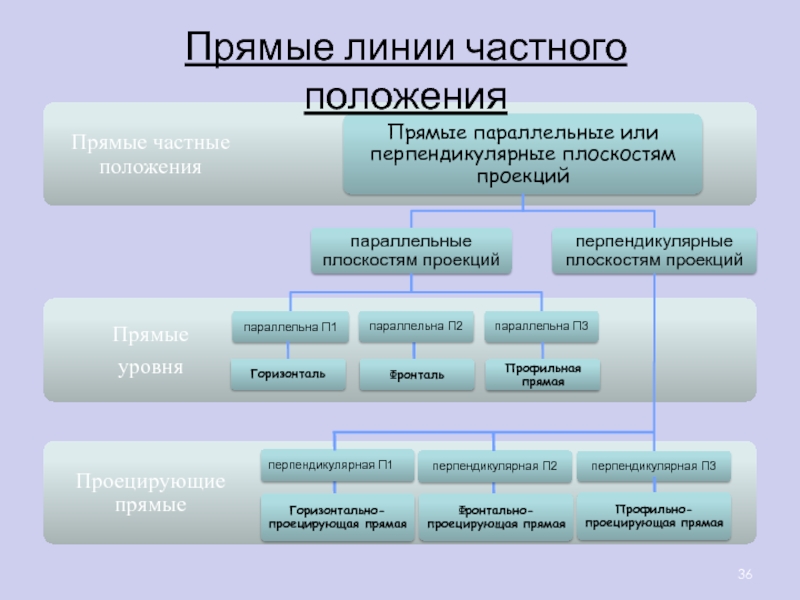
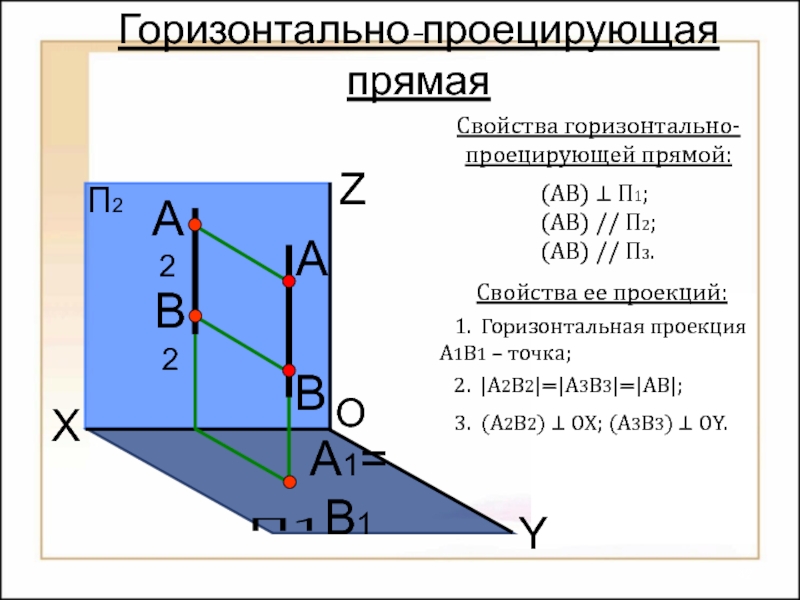
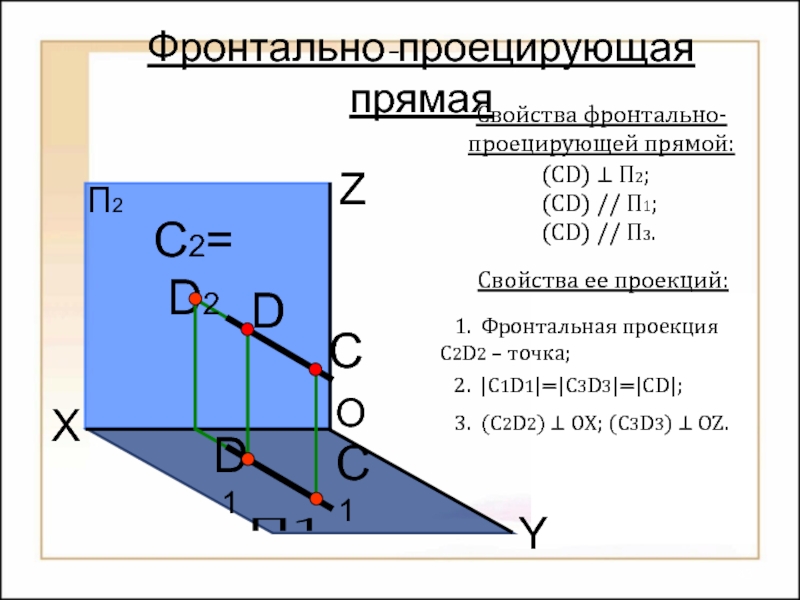
их изображений на плоскости
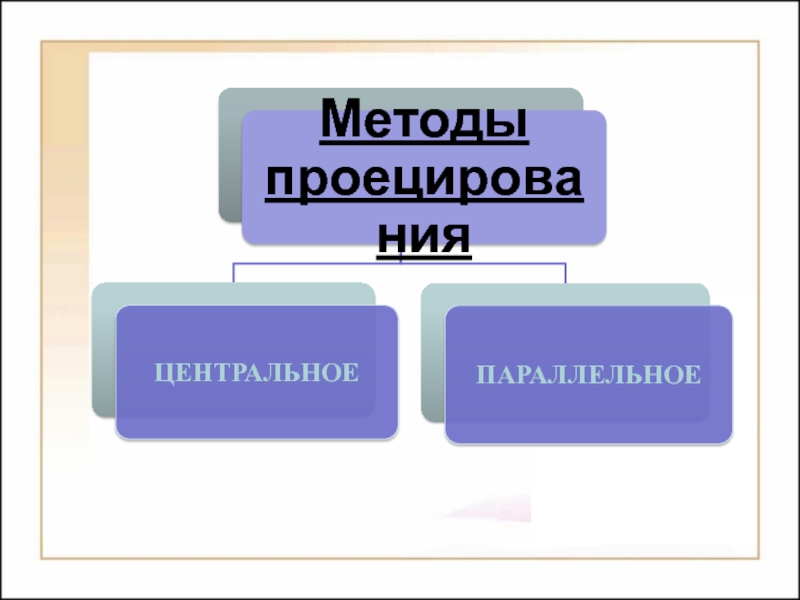
Предметом начертательной геометрии являются:
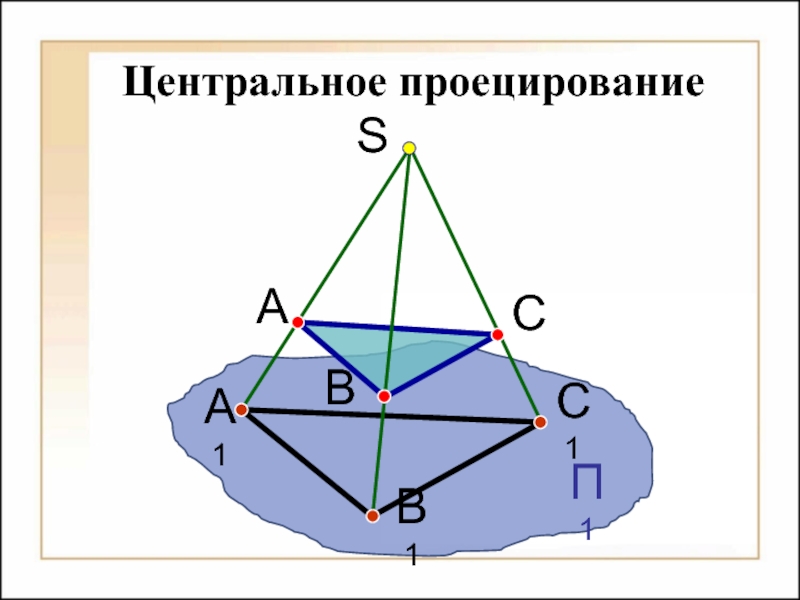
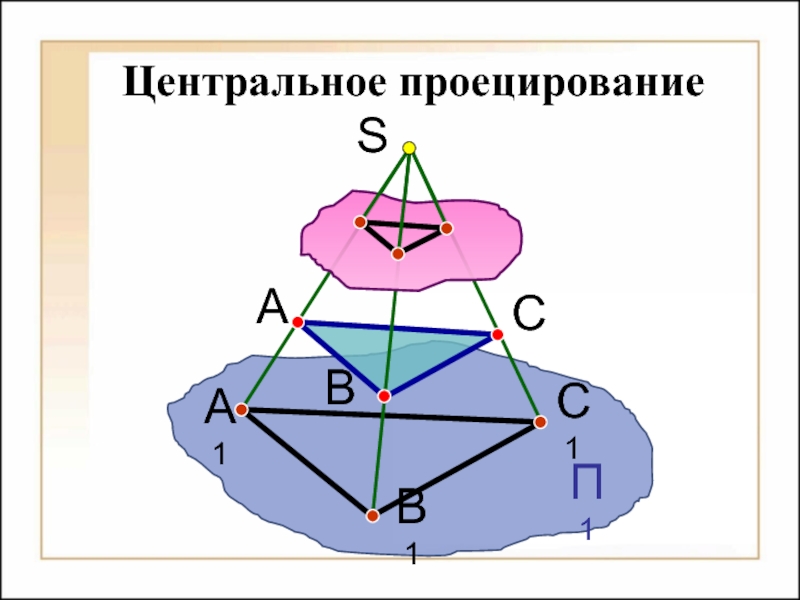
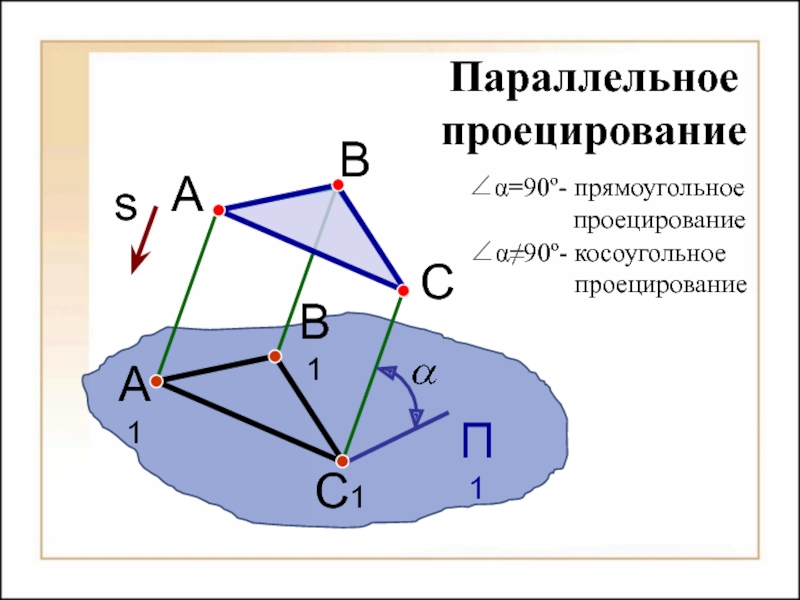
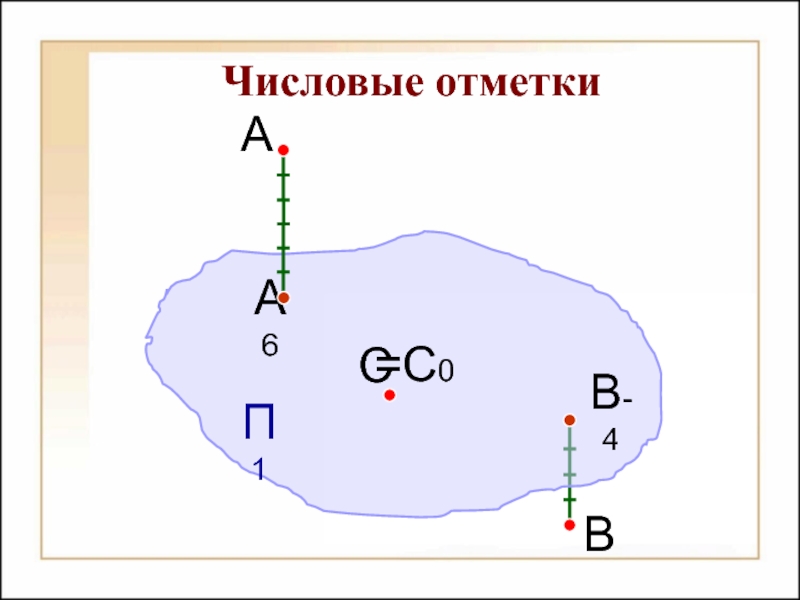
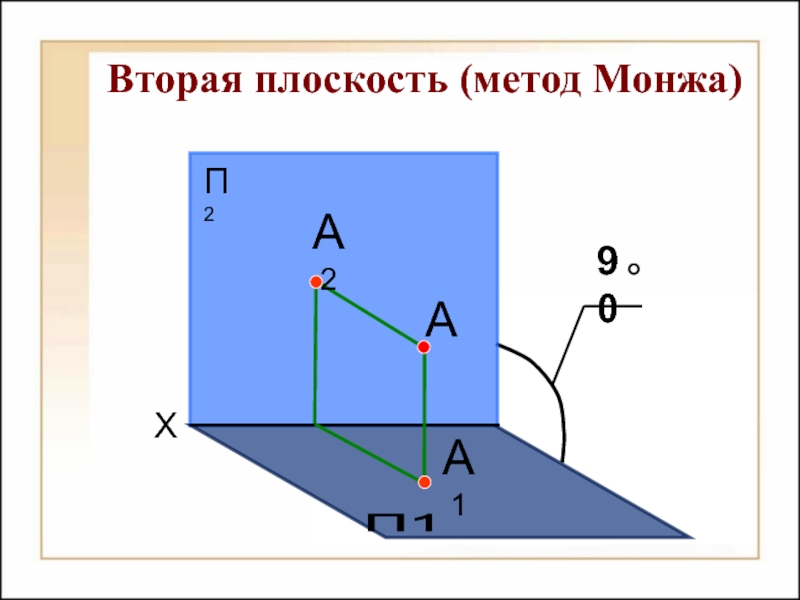
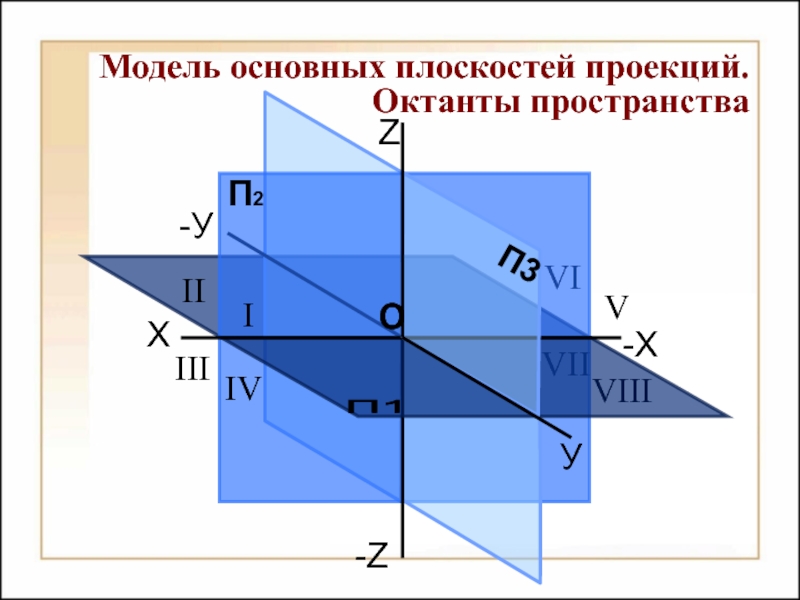
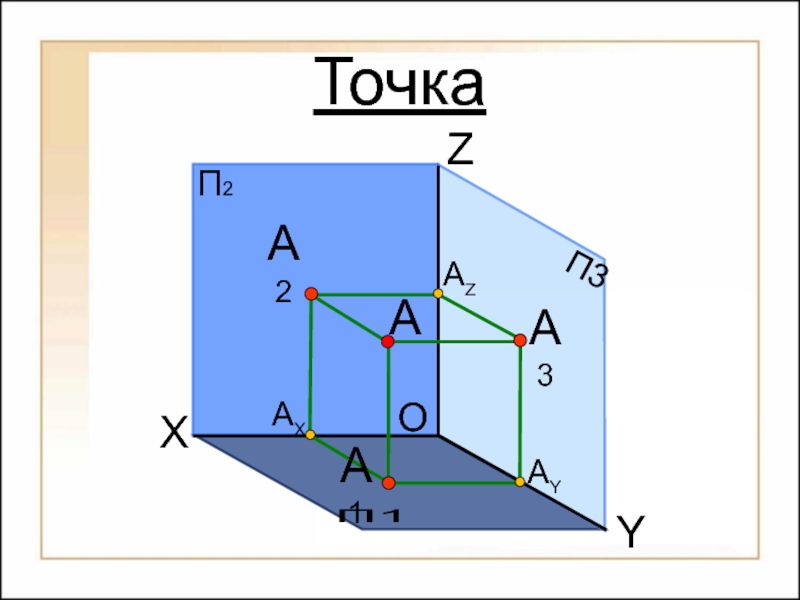
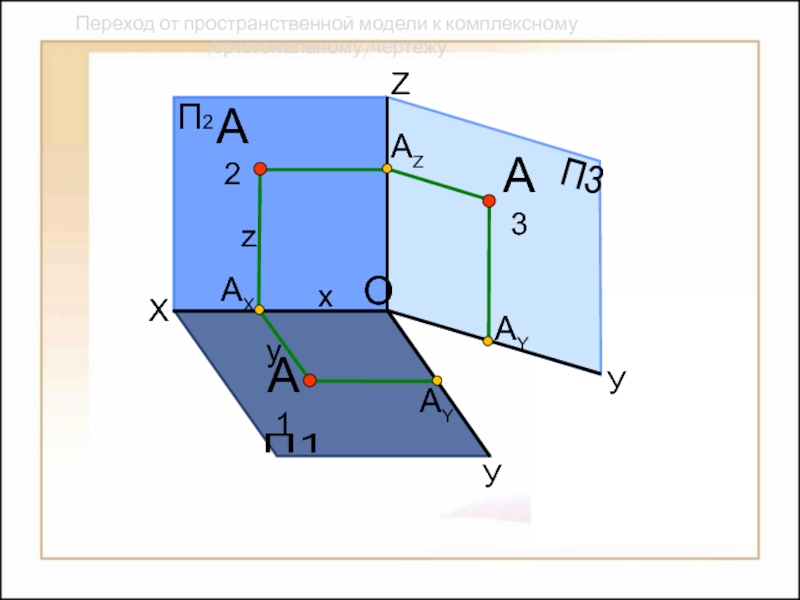
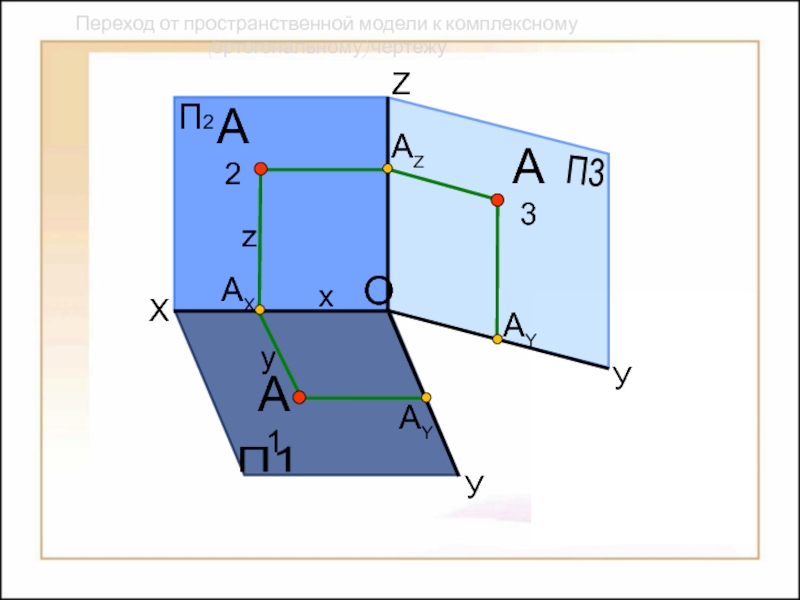
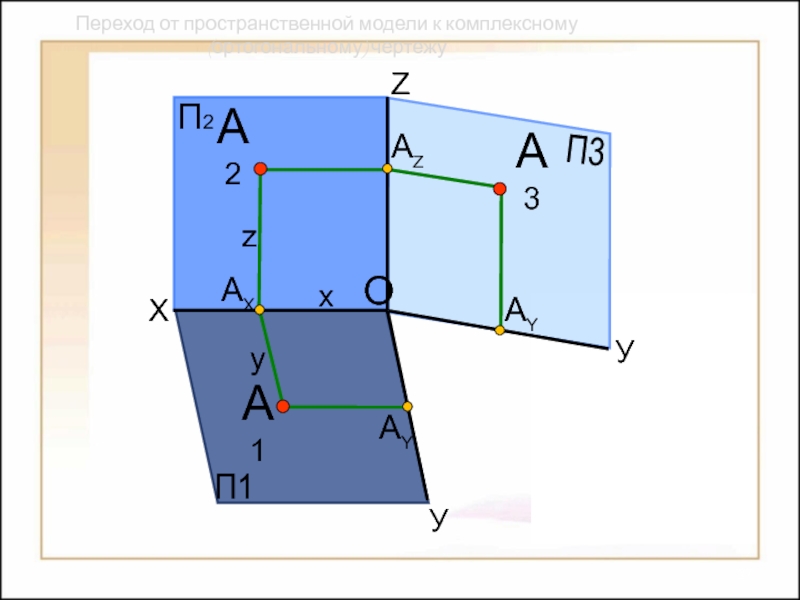
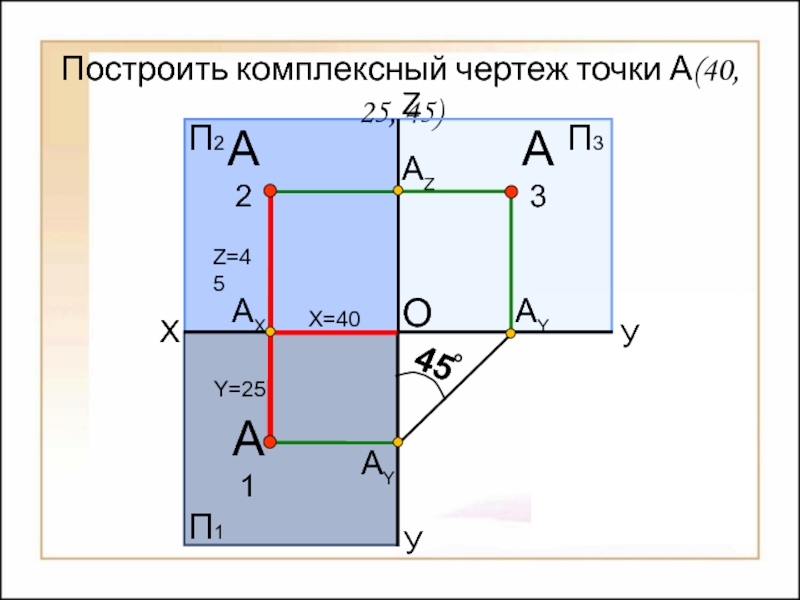
Способы построения

изображений пространственных форм на плоскости;
Исследование геометрических свойств объектов по их изображениям.
Начертательная геометрия-Раздел геометрии, в котором пространственные фигуры изучаются с помощью их изображений на плоскостиПредметом начертательной геометрии являются:

Слайд 4В начертательной геометрии используются графические методы решения задач

В начертательной геометрии используются графические методы решения задач

Слайд 5

ЛИТЕРАТУРА
Рябова И.П.Начертательная геометрия: Учебное пособие для всех форм обучения:

Издательский центр ЮУрГУ, 2014.

Бударин О.С. Начертательная геометрия. Краткий курс: Учебное пособие. – СПб.: Издательство «Лань», 2019.

ЛИТЕРАТУРАРябова И.П.Начертательная геометрия: Учебное пособие для

Слайд 6Историческая справка
С древних времён человек старался сохранить образ увиденного. Наскальная

живопись, украшенные рисунками стены жилища, посуда, предметы быта – первые

тому свидетельства.
Цивилизация развивалась, появились схемы и карты местности, изображение храмовых комплексов, жилых домов, военных сооружений, мостов, простых механизмов. Потребовалась выработка и первых общих правил представления пространственной информации на плоскости. Семь чудес света трудно представить без первых чертежей, рисунков и схем.
Египетские, греческие и римские учёные, изучая перспективу, пытались выработать некие правила представления имеющейся информации.
Историческая справкаС древних времён человек старался сохранить образ увиденного. Наскальная живопись, украшенные рисунками стены жилища, посуда, предметы

Слайд 7Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи. Первые теоретические основы

перспективы создал итальянский учёный
Историческая справка
Леон Баттиста
Альберти
(1404 -1472)

Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи. Первые теоретические основы перспективы создал итальянский учёный Историческая справкаЛеон БаттистаАльберти

Слайд 8Дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний".


Историческая справка
Леонардо да
Винчи
(1452 -1519)

Дополнил линейную перспективу учением

Слайд 9Ввел метод координат французский архитектор
Историческая справка
Жерар
Дезарг
(1593 -1662)

Ввел метод координат французский архитекторИсторическая справкаЖерарДезарг (1593 -1662)

Слайд 101795 г. - появилась "Начертательная геометрия" Гаспара Монжа, им введено

понятие «комплексный чертёж» и получены полностью обратимые изображения объемных (пространственных)

объектов на плоскости.

Историческая справка

Гаспар
Монж

(1746 -1818)

Основоположник начертательной геометрии -

1795 г. - появилась

Слайд 11Первый учебник по начертательной геометрии опубликован во Франции в 1798

г.

Россия. Развитию начертательной геометрии способствовали А. Рублёв, Дионисий, архитекторы В.Баженов,

А.Ворончихин; самоучки, механики-изобретатели И. Ползунов, И. Кулибин, И. Моторин и другие.
1810 г. – Карл Потье читает в С.-Петербурге первые лекции в Институте корпуса инженеров путей сообщения.
1821 г. – Я.А. Севастьянов (1796-1849) издает оригинальный курс начертательной геометрии на русском языке.

Историческая справка

Первый учебник по начертательной геометрии опубликован во Франции в 1798 г.Россия. Развитию начертательной геометрии способствовали А. Рублёв,

Слайд 13П1
А1
В1
С1
A
C
B
S
Центральное проецирование

П1А1В1С1ACBSЦентральное проецирование

Слайд 14С1
A
B
S
А1
C
В1
П1
Центральное проецирование

С1ABSА1CВ1П1Центральное проецирование

Слайд 15П1
А1
В1
С1
A
C
Параллельное проецирование
B
º- прямоугольное проецирование
≠º-

косоугольное

проецирование

s

П1А1В1С1ACПараллельное проецированиеBº- прямоугольное проецирование≠º- косоугольное

Слайд 16Числовые отметки
А6
A
П1
B
C
B-4
=C0

Числовые отметкиА6AП1BCB-4=C0

Слайд 17Вторая плоскость (метод Монжа)‏
X
П2
П1
А1
А
А2

Вторая плоскость (метод Монжа)‏XП2П1А1АА2

Слайд 18VIII
VII
VI
-У
X
П1
П2
П3
-X
У
Z
-Z
I
II
O
IV
V
III
‏
Модель основных плоскостей проекций. Октанты пространства

VIIIVIIVI-УXП1П2П3-XУZ-ZIIIOIVVIII‏Модель основных плоскостей проекций. Октанты пространства

Слайд 19Точка
O
П2
П1
П3
X
Y
Z
АX
АY
А1
А
А2
А3
АZ

ТочкаOП2П1П3XYZАXАYА1АА2А3АZ

Слайд 20O
X
Y
Z
АX
АY
А1
А
А2
А3
АZ
x
y
z
Точка
П2
П1
П3

OXYZАXАYА1АА2А3АZxyzТочкаП2П1П3

Слайд 21Переход от пространственной модели к комплексному (ортогональному) чертежу

Переход от пространственной модели к комплексному (ортогональному) чертежу

Слайд 22П2
П1
П3
X
Z
АX
АY
А1
А
А2
А3
АZ
Переход от пространственной модели к комплексному (ортогональному) чертежу
У
O
x
y
z

П2П1П3XZАXАYА1АА2А3АZПереход от пространственной модели к комплексному (ортогональному) чертежуУOxyz

Слайд 23АY
А1
А3
Переход от пространственной модели к комплексному (ортогональному) чертежу
АY
П1
П3
X
У
У
АZ
П2
Z
А2
АX
O
x
y
z

АYА1А3Переход от пространственной модели к комплексному (ортогональному) чертежуАYП1П3XУУАZП2ZА2АXOxyz

Слайд 24Переход от пространственной модели к комплексному (ортогональному) чертежу
П1
П3
X
У
У
O
АY
А1
А3
АY
АX
АZ
П2
Z
А2
x
y
z

Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУУOАYА1А3АYАXАZП2ZА2xyz

Слайд 25Переход от пространственной модели к комплексному (ортогональному) чертежу
П1
П3
X
У
У
АY
А1
А3
АY
O
АX
АZ
П2
Z
А2
x
y
z

Переход от пространственной модели к комплексному (ортогональному) чертежуП1П3XУУАYА1А3АYOАXАZП2ZА2xyz

Слайд 26Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
П1
П3
АY
А1
А3
АY
O
АX
АZ
П2
Z
А2
x
y
z

Переход от пространственной модели к комплексному (ортогональному) чертежуXУУП1П3АYА1А3АYOАXАZП2ZА2xyz

Слайд 27Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
П1
П3
АY
А1
А3
АY
АX
АZ
O
П2
Z
А2
x
y
z

Переход от пространственной модели к комплексному (ортогональному) чертежуXУУП1П3АYА1А3АYАXАZOП2ZА2xyz

Слайд 28Переход от пространственной модели к комплексному (ортогональному) чертежу
X
У
У
АY
А1
АY
АX
АZ
O
П2
Z
А2
П1
П3
А3
x
y
z

Переход от пространственной модели к комплексному (ортогональному) чертежуXУУАYА1АYАXАZOП2ZА2П1П3А3xyz

Слайд 291. Положение точки в пространстве определяется тремя координатами
A(x,

y, z);
2. Положение проекции точки на плоскости проекций определяется

двумя координатами
А1(x, y), А2(x, z), А3(y, z);


3. Две проекции точки определяют ее положение в пространстве;

4. Две проекции точки лежат на линии связи, перпендикулярной координатной оси.



1. Положение точки в пространстве определяется тремя координатами A(x, y, z);2. Положение проекции точки на

Слайд 30Построить комплексный чертеж точки А(40, 25, 45)
X
У
У
АY
А1
АY
АX
АZ
O
П2
Z
А2
П1
П3
А3
X=40
Y=25
Z=45

Построить комплексный чертеж точки А(40, 25, 45)XУУАYА1АYАXАZOП2ZА2П1П3А3X=40Y=25Z=45

Слайд 31Построить комплексный чертеж точки А(40, 25, 45)
X
У
У
АY
А1
АY
АX
АZ
O
П2
Z
А2
П1
П3
А3
X=40
Y=25
Z=45

Построить комплексный чертеж точки А(40, 25, 45)XУУАYА1АYАXАZOП2ZА2П1П3А3X=40Y=25Z=45

Слайд 32Линия – это множество всех последовательных положений двигающейся точки.

Прямая линия

– линия, образованная движением

точки не меняющей своего
направления.

Прямая линия

Прямая линия
может быть задана:

1. Двумя точками ей принадлежащими
2. Одной точкой и направлением линии

Линия – это множество всех последовательных положений двигающейся точки.Прямая линия – линия, образованная движением

Слайд 33Прямая линия не параллельная и не перпендикулярная ни одной из

плоскостей проекций называется – прямой общего положения.
Прямая линия общего положения
Замечание:

На

комплексном чертеже проекции прямой общего положения не параллельны и не перпендикулярны ни одной координатной оси.
Прямая линия не параллельная и не перпендикулярная ни одной из плоскостей проекций называется – прямой общего положения.Прямая

Слайд 34O
П2
П1
X
Y
Z
А1
А
А2
Прямая линия общего положения
В1
В
В2

OП2П1XYZА1АА2Прямая линия общего положенияВ1ВВ2

Слайд 35X
У
У
А1
O
П2
Z
А2
П1
П3
А3
Комплексный чертеж прямой линии общего положения
В1
В2
В3

XУУА1OП2ZА2П1П3А3Комплексный чертеж прямой линии общего положенияВ1В2В3

Слайд 36Прямые линии частного положения

Прямые линии частного положения

Слайд 37O
П2
П1
X
Y
Z
А1
А
А2
Горизонталь
В1
В
В2

OП2П1XYZА1АА2ГоризонтальВ1ВВ2

Слайд 38X
У
А1
O
П2
Z
А2
П1
П3
А3
Комплексный чертеж горизонтали
В1
В2
В3
Н.В.
Свойства горизонтали:
1. Горизонтальная проекция

горизонтали А1В1 – натуральная величина;
У
2. Фронтальная

проекция горизонтали А2В2 параллельна оси ОХ.
XУА1OП2ZА2П1П3А3Комплексный чертеж горизонталиВ1В2В3Н.В.Свойства горизонтали: 1. Горизонтальная проекция горизонтали А1В1 – натуральная величина;У

Слайд 39O
П2
П1
X
Y
Z
C1
C
С2
Фронталь
D1
D
D2

OП2П1XYZC1CС2ФронтальD1DD2

Слайд 40X
У
А1
O
П2
Z
А2
П1
П3
А3
Комплексный чертеж фронтали
В1
В2
В3
Н.В.
Свойства фронтали:
1. Фронтальная проекция

фронтали А2В2 – натуральная величина;
У
2. Горизонтальная

проекция фронтали А1В1 параллельна оси ОХ.
XУА1OП2ZА2П1П3А3Комплексный чертеж фронталиВ1В2В3Н.В.Свойства фронтали: 1. Фронтальная проекция фронтали А2В2 – натуральная величина;У

Слайд 41Свойства проекций прямых уровня
Если прямая параллельна плоскости проекций, то:

на эту плоскость проецируются в натуральную величину сама прямая и

углы наклона ее к двум другим плоскостям проекций;

проекции прямой на две другие плоскости проекций, параллельны координатным осям.

Свойства проекций прямых уровняЕсли прямая параллельна плоскости проекций, то: на эту плоскость проецируются в натуральную величину

Слайд 42O
П2
П1
X
Y
Z
А
А2
А1=В1
В
В2
Горизонтально-проецирующая прямая
Свойства горизонтально-проецирующей прямой:
(АВ)  П1;
(АВ) // П2;
(АВ) //

П3.
Свойства ее проекций:
1. Горизонтальная проекция А1В1 – точка;

2. |А2В2|=|А3В3|=|АВ|;

3. (А2В2)  OX; (А3В3)  OY.

OП2П1XYZАА2А1=В1ВВ2Горизонтально-проецирующая прямаяСвойства горизонтально-проецирующей прямой:(АВ)  П1; (АВ) // П2;(АВ) // П3.Свойства ее проекций: 1. Горизонтальная проекция

Слайд 43O
П2
П1
X
Y
Z
С
С1
D
С2=D2
Фронтально-проецирующая прямая
Свойства фронтально-проецирующей прямой:
(CD)  П2;
(CD) // П1;
(CD) //

П3.
Свойства ее проекций:
1. Фронтальная проекция С2D2 – точка;

2. |C1D1|=|C3D3|=|CD|;

3. (C2D2)  OX; (C3D3)  OZ.

D1

OП2П1XYZСС1DС2=D2Фронтально-проецирующая прямаяСвойства фронтально-проецирующей прямой:(CD)  П2; (CD) // П1;(CD) // П3.Свойства ее проекций: 1. Фронтальная проекция

Слайд 44Свойства проекций проецирующих прямых
Если прямая перпендикулярна плоскости проекций, то:

на эту плоскость она проецируются в точку;
проекции прямой

на две другие плоскости проекций проецируются в натуральную величину и перпендикулярны координатным осям.
Свойства проекций проецирующих прямыхЕсли прямая перпендикулярна плоскости проекций, то: на эту плоскость она проецируются в точку;

Похожие презентации

. Килеп җитте 8 нче Март! Укытучы апалар,бу Сезнең көнегез. Үзегез укыткан . Килеп җитте 8 нче Март! Укытучы апалар,бу Сезнең көнегез. Үзегез укыткан 361
Лекции по предмету информационные системы Раздел 2 Моделирование и разработка Лекции по предмету информационные системы Раздел 2 Моделирование и разработка 202
НОВЫЙ КОРОНАВИРУС Кто предупрежден, тот вооружен НОВЫЙ КОРОНАВИРУС Кто предупрежден, тот вооружен 188
А.П. ПЛАТОНОВ А.П. ПЛАТОНОВ 204
Графический способ решения систем уравнений Графический способ решения систем уравнений 483
Шуточный гороскоп на 2017 год Шуточный гороскоп на 2017 год 277
ДЕТЯМ О КОСМОСЕ ДЕТЯМ О КОСМОСЕ 166
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ СЕМИНАР Вводный вебинар Курчеев Валерий Сергеевич НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ СЕМИНАР Вводный вебинар Курчеев Валерий Сергеевич 227
1.ppt 1.ppt 202
М.Ю.Лермонтов 1814 - 1841 /материалы к роману М.Ю.Лермонтов 1814 - 1841 /материалы к роману "Герой нашего времени"/ 270
Физические свойства цвета Физические свойства цвета 207
Магистерская программа Государственное и муниципальное управление Магистерская программа Государственное и муниципальное управление 221
РОКОКО притворная красота Галантного века РОКОКО притворная красота Галантного века 308
Лирика Ф.И. Тютчева Лирика Ф.И. Тютчева 380
Лихарева Н. Д. студентка 1 курса магистратуры направление 38.0 4.01 Лихарева Н. Д. студентка 1 курса магистратуры направление 38.0 4.01 190
Forestry of Canada Forestry of Canada 164
IT – инфраструктура ИС IT – инфраструктура ИС 639
Разноуровневое обучение Разноуровневое обучение 559
Сергей Рыбин, Октябрь 2018, Орел rybin@adacore.com Язык Ада в современной Сергей Рыбин, Октябрь 2018, Орел rybin@adacore.com Язык Ада в современной 241
Проектирование цифровой системы телевещания поселка Проектирование цифровой системы телевещания поселка 291

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика