Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предмет вычислительной математики. Классификация погрешностей. Численное
Содержание
- 1. Предмет вычислительной математики. Классификация погрешностей. Численное
- 2. Предмет вычислительной математики. Погрешности. Численное дифференцирование.Предмет вычислительной математики
- 3. Предмет вычислительной математики. Погрешности. Численное дифференцирование.Краткий экскурс
- 4. Вычислительная математика в наше времяTianhe-2 (Китай),более 3
- 5. Специфика вычислительной математикиПредмет вычислительной математики. Погрешности. Численное
- 6. Классификация погрешностейПредмет вычислительной математики. Погрешности. Численное дифференцирование.
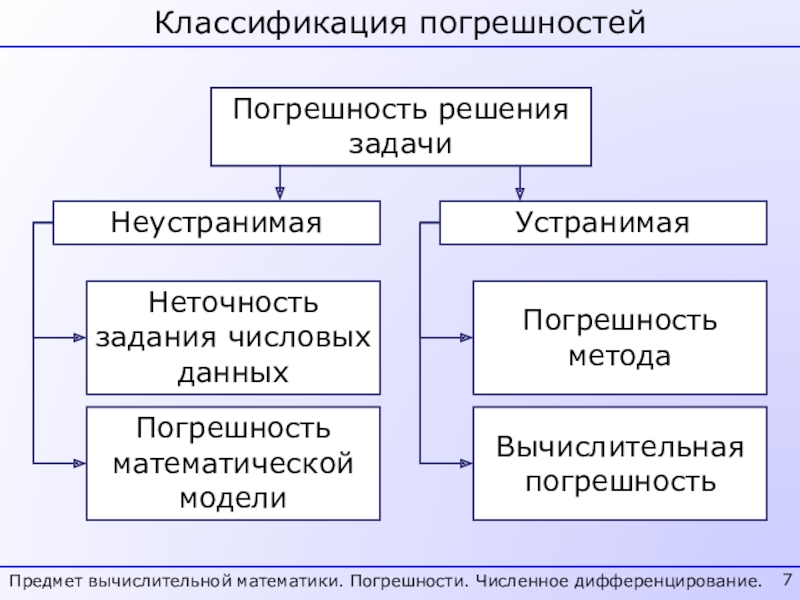
- 7. Классификация погрешностейПогрешность решения задачиНеустранимаяУстранимаяНеточность задания числовых данныхПогрешность математической моделиПогрешность методаВычислительная погрешностьПредмет вычислительной математики. Погрешности. Численное дифференцирование.
- 8. Пример – колебания математического маятникаПредмет вычислительной математики.
- 9. Вычислительная погрешностьПредмет вычислительной математики. Погрешности. Численное дифференцирование.xмаш
- 10. Иллюстрация понятия вычислительной погрешности (1) Предмет вычислительной
- 11. Предмет вычислительной математики. Погрешности. Численное дифференцирование.#define EPS 1.e-8#define
- 12. Предмет вычислительной математики. Погрешности. Численное дифференцирование.Причина –
- 13. Численное дифференцированиеПредмет вычислительной математики. Погрешности. Численное дифференцирование.
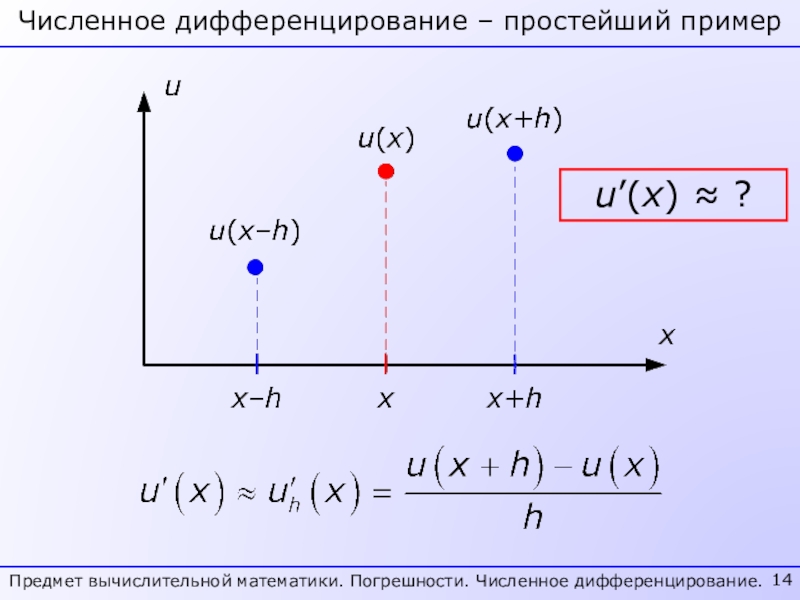
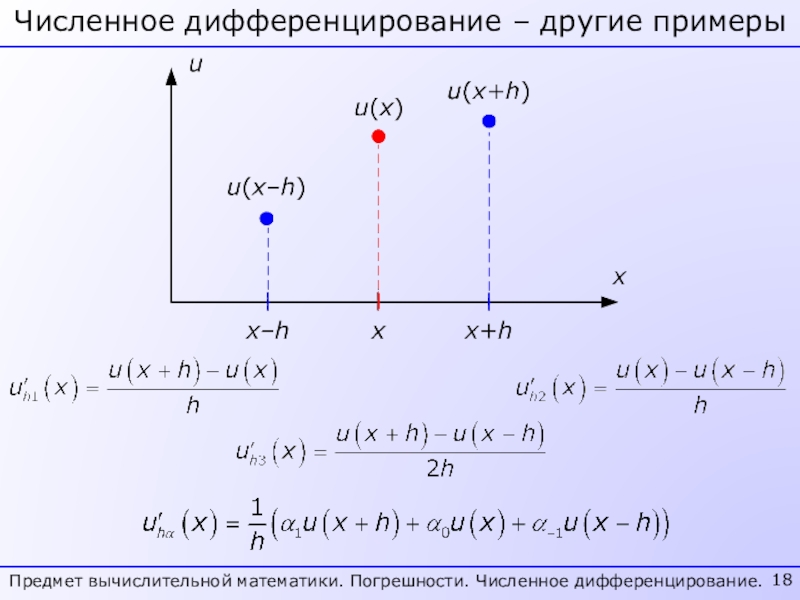
- 14. Численное дифференцирование – простейший примерПредмет вычислительной математики. Погрешности. Численное дифференцирование.u’(x) ≈ ?
- 15. Оценка погрешности методаПредмет вычислительной математики. Погрешности. Численное
- 16. Полная погрешностьПредмет вычислительной математики. Погрешности. Численное дифференцирование.Пусть
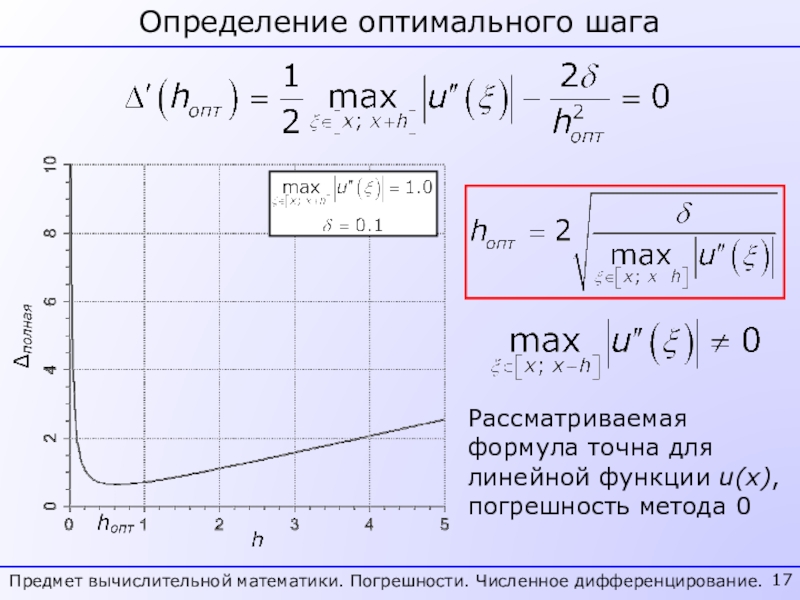
- 17. Определение оптимального шагаПредмет вычислительной математики. Погрешности. Численное
- 18. Численное дифференцирование – другие примерыПредмет вычислительной математики. Погрешности. Численное дифференцирование.
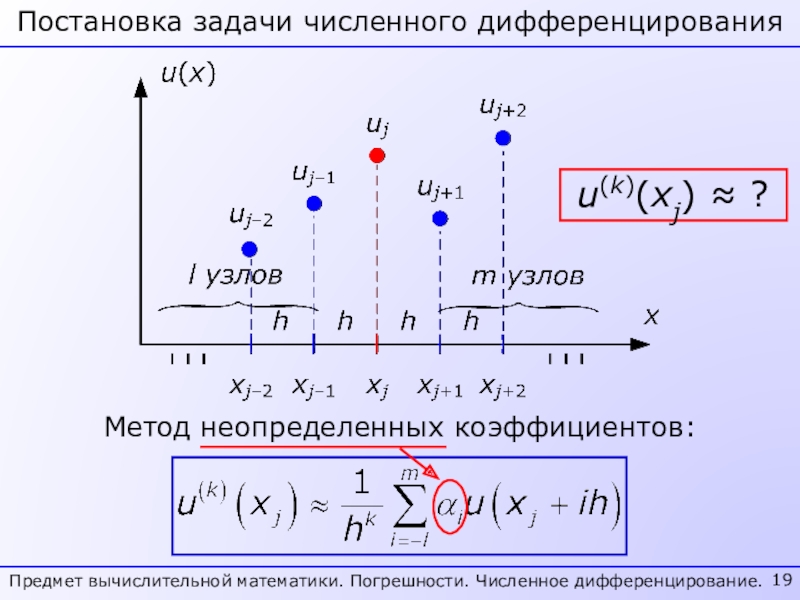
- 19. Постановка задачи численного дифференцированияПредмет вычислительной математики. Погрешности. Численное дифференцирование.u(k)(xj) ≈ ?Метод неопределенных коэффициентов:
- 20. Формирование системы уравненийПредмет вычислительной математики. Погрешности. Численное дифференцирование.Для простоты рассмотрим случай k = 1
- 21. Система уравнений для нахождения коэффициентовПредмет вычислительной математики.
- 22. Разрешимость полученной системы уравненийПредмет вычислительной математики. Погрешности.
- 23. Определитель ВандермондаПредмет вычислительной математики. Погрешности. Численное дифференцирование.
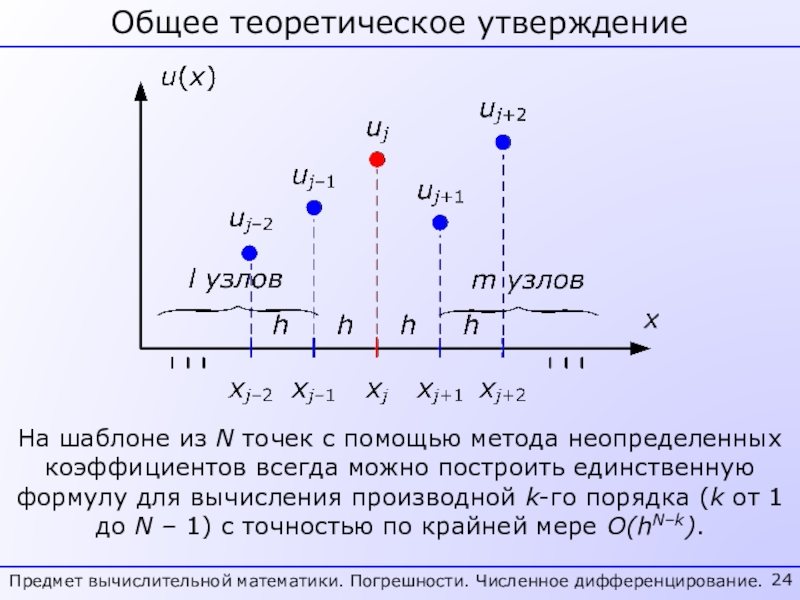
- 24. Общее теоретическое утверждениеПредмет вычислительной математики. Погрешности. Численное
- 25. ЗамечаниеПредмет вычислительной математики. Погрешности. Численное дифференцирование.
- 26. Пример использования метода неопределенных коэффициентов (1)Предмет вычислительной математики. Погрешности. Численное дифференцирование.с максимальным порядком
- 27. Предмет вычислительной математики. Погрешности. Численное дифференцирование.Пример использования метода неопределенных коэффициентов (2)
- 28. Предмет вычислительной математики. Погрешности. Численное дифференцирование.Пример использования метода неопределенных коэффициентов (3)
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Предмет вычислительной математики
Слайд 3Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Краткий экскурс в историю
1768 г.
– Леонард Эйлер, метод ломаных
Слайд 4Вычислительная математика в наше время
Tianhe-2 (Китай),
более 3 000 000 вычислительных
ядер, ~ 55 PFlops
1950-ые
Первая Советская атомная бомба
БЭСМ-6, 1 MFlops
Трехмерное моделирование
Первые
многомерные расчетыСложные трехмерные расчетные сетки
Серийные двумерные расчеты с достаточной разрешающей способностью
1970-ые
Женщины с арифмометрами, работали пока не уставали…
Кластеры типа Beowolf, ~ 10 GFlops
1990-ые
2014 год
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Слайд 5Специфика вычислительной математики
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Вычислительная математика имеет
дело не только с непрерывными, но и с дискретными объектами
→ погрешность метода;Погрешность вычислений в связи с ошибками округления;
Имеет значение обусловленность задач, т.е. чувствительность решения к малым изменениям входных данных;
Выбор вычислительного алгоритма, вообще говоря, влияет на результат вычислений;
Важная черта численного метода – экономичность, т.е. требование минимизации числа операций.
Слайд 6Классификация погрешностей
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Слайд 7Классификация погрешностей
Погрешность решения задачи
Неустранимая
Устранимая
Неточность задания числовых данных
Погрешность математической модели
Погрешность метода
Вычислительная
погрешность
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
Слайд 8Пример – колебания математического маятника
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
ΔΣ
= | φ3 – φ | = | φ3 –
φ2 + φ2 – φ1 + φ1 – φ | ≤ Δ1 + Δ2 + Δ3ΔΣ ≤ Δ1 + Δ2 + Δ3
Неустранимая погрешность – трение зависит от скорости не совсем линейно + погрешность определения g, l, начальных условий; Δ1 = | φ1 – φ |.
Погрешность метода – дифференциальное уравнение не решается точно, требуется применить какой-либо численный метод; Δ2 = | φ2 – φ1 |.
Вычислительная погрешность связана, например, с конечностью разрядной сетки; Δ3 = | φ3 – φ2 |.
Слайд 9Вычислительная погрешность
Предмет вычислительной математики. Погрешности. Численное дифференцирование.
xмаш = x·( 1
+ ε(x) ), где мерой ε(x) может служить «машинное эпсилон»
ε – наименьшее положительное число, для которого ( 1 + ε(x) )маш ≥ 1Утверждение 1.1. Относительная погрешность округления при представлении вещественного числа в ЭВМ ε ≈ 2–t, где t – разрядность мантиссы.
В расчетах с двойной точностью t = 52, εdouble ≈ 10–16
Машинное представление вещественных чисел:
Слайд 10Иллюстрация понятия вычислительной погрешности (1)
Предмет вычислительной математики. Погрешности. Численное
дифференцирование.
Приближенное вычисление значения синуса с помощью разложения в ряд Тейлора
Ряд
сходится для любого значения xНапишем программу для вычисления значения синуса при:
X1 = π / 6 ≈ 0.52366
X2 = 12π + π / 6 ≈ 38.22277
(Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа. – М.: Физматлит, 2001. – С. 439.)
Слайд 11Предмет вычислительной математики. Погрешности. Численное дифференцирование.
#define EPS 1.e-8
#define X 0.52366
...
int i, k
= 0;
double curr_sum = 0.0, curr_sum_old = 0.0, fact;
do {
fact
= 1.0;for ( i = 1; i<= 2*k+1; i++ )
fact *= i;
curr_sum_old = curr_sum;
curr_sum += pow( -1, k) * pow( X, 2*k+1 ) / fact;
k++;
} while ( fabs( curr_sum - curr_sum_old ) > EPS );
Результат расчета значения синуса:
Иллюстрация понятия вычислительной погрешности (2)
Для X1 = 0.52366: 0.500053…
Для X2 = 38.22277: 1.165079…
Слайд 12Предмет вычислительной математики. Погрешности. Численное дифференцирование.
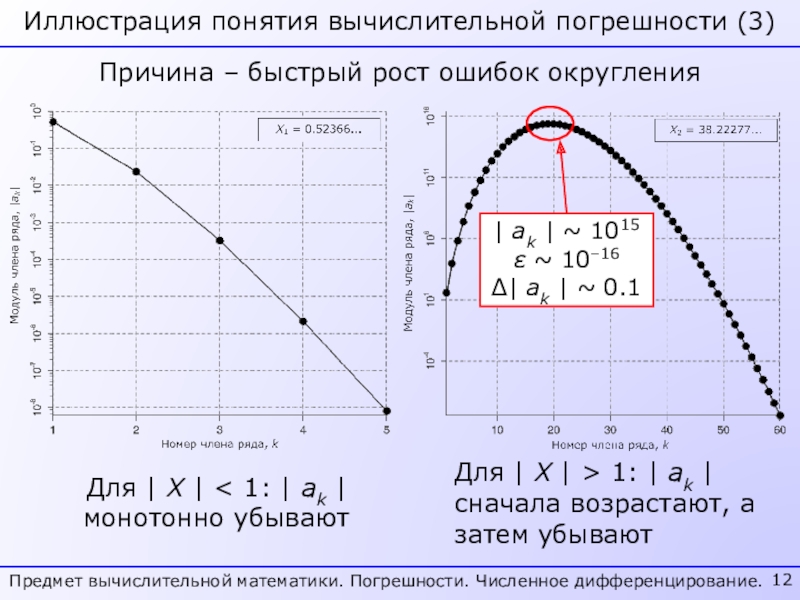
Причина – быстрый рост ошибок
округления
Для | X | > 1: | ak | сначала
возрастают, а затем убываютИллюстрация понятия вычислительной погрешности (3)
Для | X | < 1: | ak | монотонно убывают
| ak | ~ 1015
ε ~ 10–16
Δ| ak | ~ 0.1