Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление чисел в компьютере
Содержание
- 1. Представление чисел в компьютере
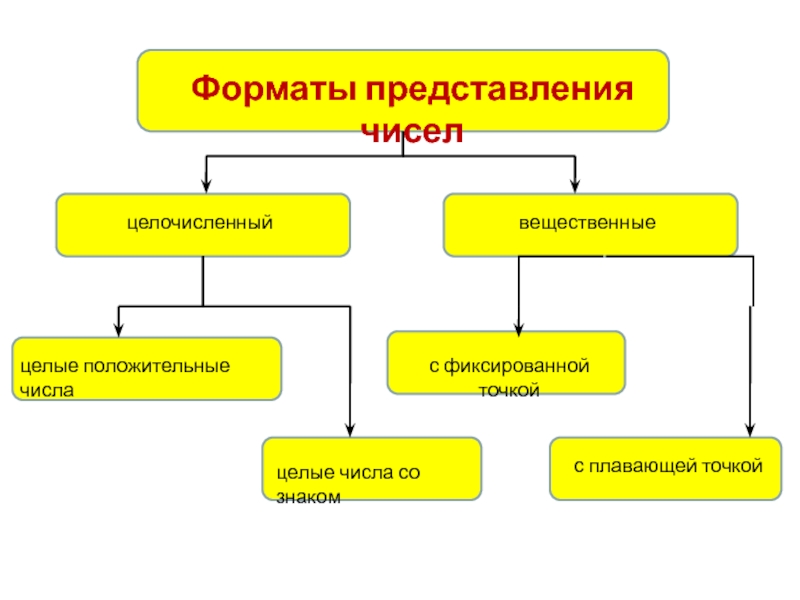
- 2. Форматы представления чиселцелочисленныйвещественныецелые положительные числацелые числа со знакомс фиксированной точкойс плавающей точкой
- 3. ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ В ФОРМАТЕ С
- 4. ЦЕЛЫЕ НЕОТРИЦАТЕЛЬНЫЕ ЧИСЛАДля хранения целых неотрицательных чисел
- 5. ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМПредставление в компьютере положительных
- 6. ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМДля n-разрядного представления со
- 7. Троицкий Д.И. Информатика САПР 1 семестрКоды: прямой,
- 8. Троицкий Д.И. Информатика САПР 1 семестрКоды: прямой,
- 9. Троицкий Д.И. Информатика САПР 1 семестрПрямой код
- 10. Троицкий Д.И. Информатика САПР 1 семестрОбратный код
- 11. Дополнительный код числа Дополнительный код строится только для
- 12. Алгоритм получения дополнительного кода отрицательного числа.
- 13. Модифицированный кодПри сложении чисел, меньших единицы, может
- 14. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКОГО ДЕЙСТВИЯВыполнить арифметическое действие 2010 –
- 15. ПЕРЕВОД ДОПОЛНИТЕЛЬНОГО КОДА В ДЕСЯТИЧНОЕ ЧИСЛОВ 16-разрядном
- 16. ПЕРЕВОД ДОПОЛНИТЕЛЬНОГО КОДА В ДЕСЯТИЧНОЕ ЧИСЛОВ 16-разрядном
- 17. Выполняя на компьютере вычисления с целыми числами,
- 18. Представление чисел в формате с плавающей запятой. Представление вещественных чисел
- 19. ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ В ФОРМАТЕ С
- 20. В двух байтовом формате представление
- 21. Данное число может быть представлено в четырехбайтовом
- 22. ПРИВЕДЕНИЕ ЧИСЛА С ПЛАВАЮЩЕЙ ЗАПЯТОЙ К НОРМАЛИЗОВАННОЙ
- 23. ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО ЧИСЛА И ЕГО ТОЧНОСТИМаксимальное
- 24. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ В ФОРМАТЕ
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Представление чисел
в компьютере
Изучаемые вопросы:
Представление информации в компьютере.
Представление
целых чисел.
Слайд 2Форматы представления чисел
целочисленный
вещественные
целые положительные числа
целые числа со знаком
с фиксированной точкой
с
плавающей точкой
Слайд 3ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ В ФОРМАТЕ
С ФИКСИРОВАННОЙ ЗАПЯТОЙ
Целые числа в
компьютере хранятся в памяти в формате
с фиксированной запятой.
При хранении чисел в памяти в формате с фиксированной запятой каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т.е. вне разрядной сетки.Достоинства:
простота и наглядность представления чисел;
простота алгоритмов реализации арифметических операций (вычитание заменяется сложением).
Недостаток:
конечный диапазон представления величин, недостаточный для решения задач, в которых используются очень малые и/или очень большие числа.
1010=10102
Слайд 4ЦЕЛЫЕ НЕОТРИЦАТЕЛЬНЫЕ ЧИСЛА
Для хранения целых неотрицательных чисел отводится
одна ячейка
памяти (8 битов).
Минимальное число:
Максимальное число:
Для n-разрядного представления
максимальное целое неотрицательное число равно 2n – 1.Минимальное число равно 0.
Максимальное число равно 25510.
111111112 = 1000000002 -1 = 28 – 1 = 25510
Диапазон изменения целых неотрицательных чисел от 0 до 255.
Слайд 5ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ
Представление в компьютере положительных чисел
с использованием
формата «знак-величина» называется прямым кодом числа.
Старший (левый) разряд отводится под
знак числа: 0 – положительное число,
1 – отрицательное число.
Для хранения целых чисел со знаком отводится
две ячейки памяти (16 битов).
Для хранения больших целых чисел со знаком отводится
четыре ячейки памяти (32 бита).
Слайд 6ЦЕЛЫЕ ЧИСЛА СО ЗНАКОМ
Для n-разрядного представления со знаком (с учетом
выделения одного разряда на знак):
максимальное положительное число равно 2n-1
– 1, минимальное отрицательное число равно – 2n-1
Диапазон хранения
целых чисел со знаком
от – 32 768 до 32 767.
Диапазон хранения
больших целых чисел со знаком
от – 2 147 483 648 до 2 147 483 647.
А10 = 215 – 1 = 3276710
А10 = – 215 = – 3276810
А10 = 231 – 1 = 2 147 483 647 10
А10 = – 231 = – 2 147 483 648 10
Слайд 7Троицкий Д.И. Информатика САПР 1 семестр
Коды: прямой, обратный, дополнительный, модифицированный
Одним
из способов выполнения операции вычитания является замена знака вычитаемого на
противоположный и прибавление его к уменьшаемому:A – B = A + (–B).
Этим операцию арифметического вычитания заменяют операцией алгебраического сложения. Последняя и становится основной операцией.
Для машинного представления отрицательных чисел используют коды:
прямой,
обратный,
дополнительный,
модифицированный.
Слайд 8Троицкий Д.И. Информатика САПР 1 семестр
Коды: прямой, обратный, дополнительный, модифицированный
Прямой
код обычно используется при хранении чисел в запоминающем устройстве, а
обратный и дополнительный коды — при выполнении над числами арифметических и некоторых других операций. При пересылках из запоминающего устройства в арифметическое и обратно числа перекодируются.Все три кода состоят из кода знака (число отведённых разрядов l), кода целой части (m) и кода дробной части (n) числа. Сумма d =l+т+n называется длиной кода. Как правило l, т и n фиксированы. В случае целых чисел n=0, для правильных дробей обычно т=0, когда все числа одного знака, l=0.
Для положительных чисел код знака обозначается последовательностью нулей, для отрицательных — последовательностью единиц. Для положительных чисел прямой, обратный и дополнительный коды совпадают.
Слайд 9Троицкий Д.И. Информатика САПР 1 семестр
Прямой код числа
При кодировании прямым
n-разрядным двоичным кодом один разряд (как правило, самый старший) отводится
для знака числа. Остальные n-1 разрядов - для значащих цифр. Значение знакового разряда равно 0 для положительных чисел, 1 - для отрицательных.где - значение цифры в i-ом разряде, q –основание системы счисления.
Пример
. Таким образом, прямой код положительного числа совпадает с самим числом, а прямой код отрицательного числа отличается от самого числа единицей в старшем разряде.
Слайд 10Троицкий Д.И. Информатика САПР 1 семестр
Обратный код числа
Частное правило образования
обратного кода для отрицательных двоичных чисел. Для преобразования прямого кода
двоичного отрицательного числа в обратный код и наоборот необходимо знаковый разряд оставить без изменения, а в остальных разрядах 0 заменить на 1, а 1 на 0.Пример: А1 = 0,11010; [А1]обр = 011010 (без изменений);
А2 = -0,11010; [А2]обр = 100101.
Обратный код двоичного числа является дополнением модуля числа до наибольшего числа без знака, умещающегося в разрядную сетку, т.е. до величины 1,111…1.
Обратный код строится только для отрицательного числа. Обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное значение.
Пример:+1210=11002=0_1100(прямой)=0_0011(обратный)
-15.2510=-1111.012=1_1111.01(прямой)=1_0000.10(обр.)
Слайд 11Дополнительный код числа
Дополнительный код строится только для отрицательного числа. Использование
прямого кода усложняет структуру компьютера. В этом случае операция сложения
двух чисел, имеющих разные знаки, должна быть заменена на операцию вычитания меньшей величины из большей и присвоения результату знака большей величины. Введение дополнительного кода позволяет заменить вычитание на обычное сложение, что упрощает устройство процессора.Таким образом, для преобразования прямого кода q-ичного отрицательного числа в дополнительный , надо преобразовать его в обратный код и в младший разряд добавить 1.
Примеры:
Слайд 12Алгоритм получения дополнительного кода отрицательного числа.
Для получения дополнительного k-разрядного кода
отрицательного числа необходимо:
модуль отрицательного числа представить прямым кодом в k
двоичных разрядах; значение всех бит инвертировать:все нули заменить на единицы, а единицы на нули(таким образом, получается k-разрядный обратный код исходного числа);
к полученному обратному коду прибавить единицу.
При выполнении операции сложения с помощью специальных кодов знаковые разряды участвуют в сложении также как цифровые разряды. Знаковые разряды и цифры переноса из старшего цифрового разряда складываются как одноразрядные двоичные коды. Если при этом формируется перенос из знакового разряда, то он добавляется в младший разряд результата при использовании обратного кода и отбрасывается при использовании дополнительного кода.
Слайд 13Модифицированный код
При сложении чисел, меньших единицы, может получиться результат, по
абсолютной величине больший единицы, что ведет к искажению результатов вычислений.
Переполнение разрядной сетки легко обнаружить, используя модифицированный прямой, модифицированный обратный или модифицированный дополнительный коды. Отличие модифицированных кодов от обычных заключается в том, что на изображение знака числа отводится два разряда. “Плюс” изображается двумя нулями, а ”минус” – двумя единицами.Например, обратные модифицированные коды чисел А1 = 0,11010 и А = -0,11010 запишутся в виде [А1]обр = 00,11010; [А2]обр = 11,00101.
Слайд 14ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКОГО ДЕЙСТВИЯ
Выполнить арифметическое действие 2010 – 3010 в 16-разрядном
компьютерном представлении.
00000000 000101002
11111111 111000102
11111111 111101102
2010 – 3010 11111111 111101102
+
+
Дополнительный
кодСлайд 15ПЕРЕВОД ДОПОЛНИТЕЛЬНОГО КОДА В ДЕСЯТИЧНОЕ ЧИСЛО
В 16-разрядном компьютерном представлении
2010 –
3010 11111111 111101102
Переведем полученный дополнительный код в десятичное число:
Инвертируем дополнительный код: 00000000 00001001
2. К полученному коду прибавим 1 (получим модуль отрицательного числа):
00000000 00001010
3. Переведем в десятичное число и припишем знак отрицательного числа: -10
Слайд 16ПЕРЕВОД ДОПОЛНИТЕЛЬНОГО КОДА В ДЕСЯТИЧНОЕ ЧИСЛО
В 16-разрядном компьютерном представлении
2010 –
3010 11111111 111101102
Переведем полученный дополнительный код в десятичное число:
Отнимем 1 от дополнительного кода: 11111111 11110101
2. Инвертируем полученное число:
00000000 00001010
3. Переведем в десятичное число и припишем знак отрицательного числа: -10
Слайд 17Выполняя на компьютере вычисления с целыми числами, нужно помнить
об
ограниченности диапазона
допустимых значений.
Выход результата за границы
допустимого диапазона называется
переполнением.Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора, но результаты могут оказаться неправильными.
ОСОБЕННОСТИ РАБОТЫ С ЦЕЛЫМИ ЧИСЛАМИ
Слайд 19ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ В ФОРМАТЕ
С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
Вещественные числа хранятся
и обрабатываются в компьютере в формате с плавающей запятой
(положение
запятой в записи числа может изменяться).
Формат чисел с плавающей запятой базируется на экспоненциальной форме записи:
А = m qn,
где m – мантисса числа,
q – основание системы счисления,
n – порядок числа.
Для однозначности представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:
1/n ≤ |m| < 1,
т.е. мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля.
С фиксированной точкой - 25.43
С плавающей точкой – 0.2543 * ; 2.543 * ; 254.3*
С плавающей запятой удобно представлять числа очень близкие к нулю.
Слайд 20 В двух байтовом формате представление вещественного числа первые
байт и три разряда второго байта выделяются для размещения мантиссы,
в остальных разрядах второго байта размещаются порядок числа, знаки числа и порядка. В 4-байтовом формате представления вещественного числа первые три байта выделяются для размещения мантиссы, в четвертом байте размещаются порядок числа, знаки числа и порядка.
Слайд 21Данное число может быть представлено в четырехбайтовом формате (32 бита)
следующим образом (см. рис.).
На мантиссу отводится 23 бита, поэтому максимальная
величина мантиссы равна 223 —1 = 8 388 607, т.е. 7 десятичных цифр.Компьютер при вычислениях отбрасывает лишние цифры в мантиссе, поэтому все вычисления с вещественными числами всегда выполняются приближенно (с ошибкой). Вещественные числа обрабатываются в компьютере медленнее, чем целые.
Слайд 22ПРИВЕДЕНИЕ ЧИСЛА С ПЛАВАЮЩЕЙ ЗАПЯТОЙ К НОРМАЛИЗОВАННОЙ ФОРМЕ
Диапазон изменения чисел
определяется количеством разрядов, отведенных для хранения порядка числа,
а точность
(количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы. Преобразуем десятичное число 888,888 в экспоненциальную форму с нормализованной мантиссой:
888,888 = 0,888888 103
Число в форме с плавающей запятой занимает в памяти компьютера четыре байта (число обычной точности) или восемь байтов (число двойной точности).
Нормализованная мантисса m = 0,888888, порядок n = 3.
При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Слайд 23ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОГО ЧИСЛА
И ЕГО ТОЧНОСТИ
Максимальное значение порядка числа составит
11111112 = 12710, следовательно, максимальное число:
2127 = 1,7014118346046923173168730371588 1038.
Максимальное
значение положительной мантиссы:223 – 1 ≈ 223 = 2(102,3) ≈ 10002,3 = 10(32,3) ≈ 107.
Максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 1038, т.к. количество значащих цифр десятичного числа ограничено 7 разрядами).
Задача. Определить максимальное число и его точность для формата чисел обычной точности, если для хранения порядка и его знака отводится 8 разрядов, а для хранения мантиссы и ее знака – 24 разряда.
Слайд 24АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ
В ФОРМАТЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
При сложении
и вычитании чисел в формате с плавающей запятой сначала производится
выравнивание порядков (меньший по модулю порядок числа увеличивается до величины большего по модулю порядка числа, а мантисса уменьшается в такое же количество раз), а затем сложение или вычитание мантисс.При умножении чисел в формате с плавающей запятой порядки складываются, а мантиссы перемножаются.
При делении из порядка делимого вычитается порядок делителя, а мантисса делится на мантиссу делителя.
После выполнения арифметической операции производится нормализация.
Выполнить арифметические операции с числами 0,1 25 и 0,1 23.