Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление чисел в компьютерных системах
Содержание
- 1. Представление чисел в компьютерных системах
- 2. ТЕМЫКодирование и декодирование информации.Представление чисел в компьютере.Арифметические
- 3. 1. Кодирование и декодирование информации
- 4. Основные способы передачи информации в социотехнических системах Наполнение знаков и сигналов смыслом делает их СИМВОЛАМИ
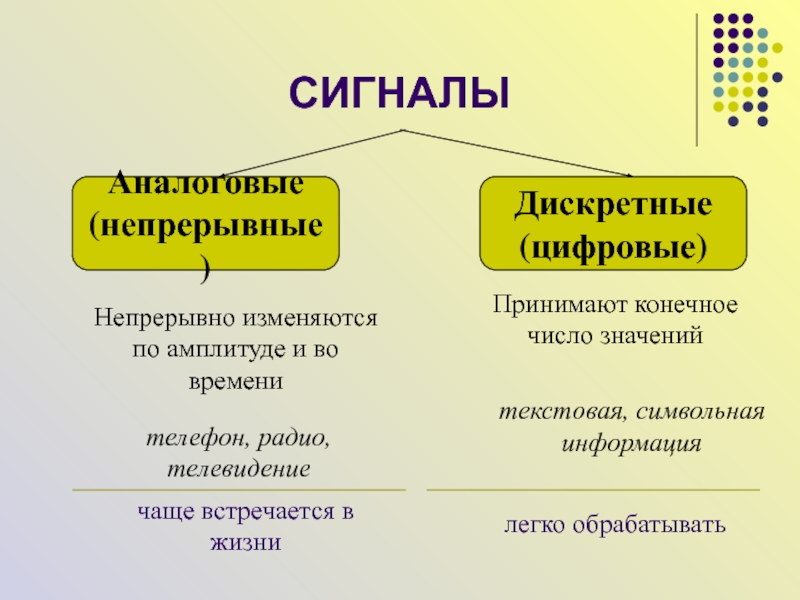
- 5. СИГНАЛЫ
- 6. Кодирование и декодированиеДля обмена информацией с другими
- 7. Способы кодирования информацииДля кодирования одной и той
- 8. Способы кодирования информацииВыбор способа кодирования информации может
- 9. Телеграфный аппарат БодоРавномерный телеграфный код был изобретен
- 10. Двоичное кодирование в компьютереВся информация, которую обрабатывает
- 11. Двоичное кодирование — это кодирование информации при помощи
- 12. Почему двоичное кодированиеС точки зрения технической реализации
- 13. 2. Представление чисел в компьютере.
- 14. Для работы с числами человек использует в
- 15. Целые числа.Целые числа без знака (только положительные)Целые
- 16. Представление целых чиселЯчейка - объем памяти, предоставленный
- 17. Как представляются в компьютере целые числа?
- 18. Диапазоны значений целых чисел без знака
- 19. Число 3910 = 100111 2 в однобайтовом
- 20. Целые числа со знаком
- 21. Целые числа со знаком.В компьютерной технике применяются
- 22. Положительные числа в прямом, обратном и
- 23. 2. Обратный код. Получается инвертированием
- 24. Прямой код числа.В знаковый разряд помещается цифра
- 25. Обратный код числа.Получается инвертированием всех цифр двоичного
- 26. Дополнительный код числа.Получается образованием обратного кода с
- 27. Представление целых отрицательных чиселОтрицательные числа в памяти
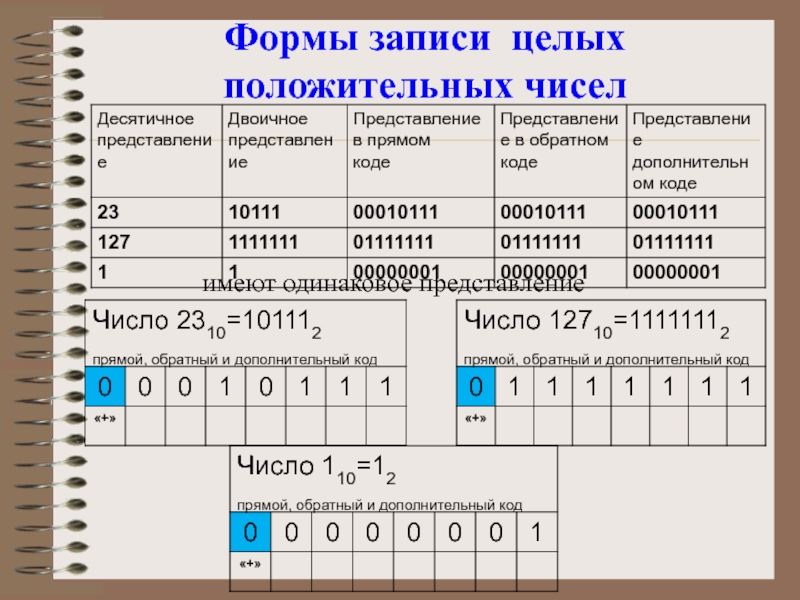
- 28. Формы записи целых положительных чиселимеют одинаковое представление
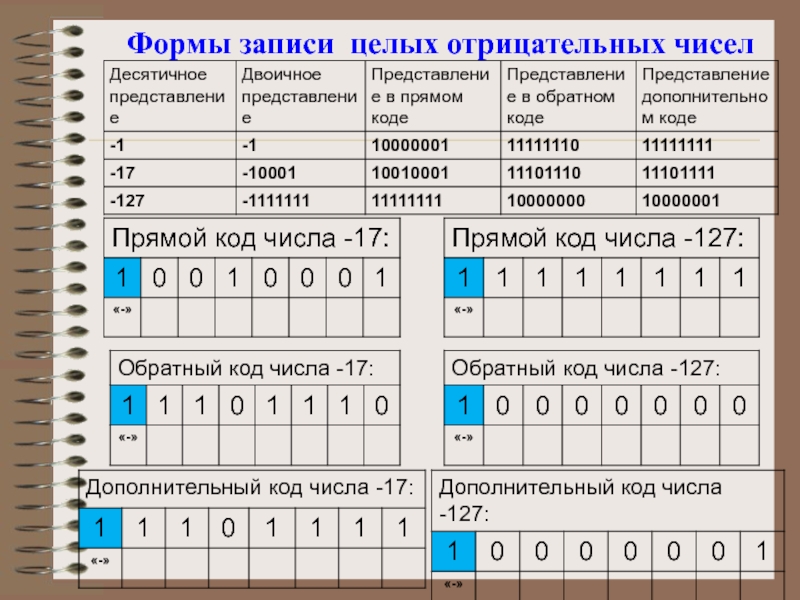
- 29. Формы записи целых отрицательных чисел
- 30. 3. Арифметические действия над целыми числами.
- 31. Сложение0+0=00+1=11+0=11+1=101101+110 =100111 1 0 11 1
- 32. 1 0 1 1 1 0 11 1 0 0 1 1 0+1011101+1100110 =11000011111010101011
- 33. Умножение0 . 0=00 . 1=01 .
- 34. В большинстве компьютеров операция вычитание не используется.
- 35. Деление выполняется по правилам математики, не
- 36. Операции над числами с фиксированной точкой.
- 37. 1. А и В положительные.
- 38. 2. А положительное, B отрицательное
- 39. 3. А положительное, B отрицательное
- 40. 4. А и В отрицательные.
- 41. 5. А и В положительные,
- 42. 6. А и В отрицательные, сумма абсолютных
- 43. 1. А и В положительные. Здесь нет
- 44. 2. А положительное, B отрицательное и
- 45. 3. А положительное, B отрицательное
- 46. 4. А и В отрицательные.Например:
- 47. Что такое переполнение?Выход результатов вычислений за границы
- 48. 4. Арифметические операции над числами с плавающей точкой.
- 49. Представление чисел с плавающей точкой.
- 50. Например, число 25,324 можно записать в таком
- 51. Получается, что представление числа в форме с
- 52. Иначе говоря, мантисса меньше единицы и первая
- 53. Для представления вещественных чисел (конечных и бесконечных
- 54. Пусть в памяти компьютера вещественное число представляется
- 55. Что такое машинный порядок? В семи двоичных
- 56. Итак, машинный порядок смещён относительно математического на
- 57. Теперь мы можем записать внутреннее представление числа
- 58. Число в форме с плавающей точкой занимает
- 59. Для того, чтобы получить внутреннее представление отрицательного
- 60. Задание.Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой.
- 61. Решение.-100,12= -0,1001*211Мантисса -0,1001Порядок 11 Машинный порядок 11+100 0000=100011.
- 62. Спасибо за внимание
- 63. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ТЕМЫ
Кодирование и декодирование
информации.
Представление чисел в компьютере.
Арифметические действия над целыми числами.
Арифметические
операции над числами с плавающей точкой.
Слайд 4Основные способы передачи информации
в социотехнических системах
Наполнение знаков и
сигналов смыслом делает их СИМВОЛАМИ
Слайд 6Кодирование и декодирование
Для обмена информацией с другими людьми человек использует
естественные языки. Наряду с естественными языками были разработаны формальные языки
для профессионального применения их в какой-либо сфере. Представление информации с помощью какого-либо языка часто называют кодированием.Код — набор символов (условных обозначений) для представления информации.
Код — система условных знаков (символов) для передачи, обработки и хранения информации(со общения).
Кодирование — процесс представления информации (сообщения) в виде кода.
Все множество символов, используемых для кодирования, называется алфавитом кодирования. Например, в памяти компьютера любая информация кодируется с помощью двоичного алфавита, содержащего всего два символа: 0 и1.
Декодирование- процесс обратного преобразования кода к форме исходной символьной системы, т.е. получение исходного сообщения. Например: перевод с азбуки Морзе в письменный текст на русском языке.
В более широком смысле декодирование — это процесс восстановления содержания закодированного сообщения. При таком подходе процесс записи текста с помощью русского алфавита можно рассматривать в качестве кодирования, а его чтение — это декодирование.
Слайд 7Способы кодирования информации
Для кодирования одной и той же информации могут
быть использованы разные способы;
их выбор зависит от ряда обстоятельств:
цели кодирования,
условий,
имеющихся средств.
Если надо записать текст в темпе речи — используем стенографию; если надо передать текст за границу — используем английский алфавит; если надо представить текст в виде, понятном для грамотного русского человека, — записываем его по правилам грамматики русского языка.
«Здравствуй, Саша!»
«Zdravstvuy, Sasha!»
Слайд 8Способы кодирования информации
Выбор способа кодирования информации может быть связан с
предполагаемым способом ее обработки.
Покажем это на примере представления чисел —
количественной информации. Используя русский алфавит, можно записать число "тридцать пять". Используя же алфавит арабской десятичной системы счисления, пишем «35». Второй способ не только короче первого, но и удобнее для выполнения вычислений. Какая запись удобнее для выполнения расчетов: "тридцать пять умножить на сто двадцать семь" или "35 х 127"? Очевидно — вторая.Слайд 9Телеграфный аппарат Бодо
Равномерный телеграфный код был изобретен французом Жаном Морисом
Бодо в конце XIX века. В нем использовалось всего два
разных вида сигналов. Не важно, как их назвать: точка и тире, плюс и минус, ноль и единица. Это два отличающихся друг от друга электрических сигнала. Длина кода всех символов одинаковая и равна пяти. В таком случае не возникает проблемы отделения букв друг от друга: каждая пятерка сигналов — это знак текста. Поэтому пропуск не нужен.Код называется равномерным, если длина кода всех символов равна.
Код Бодо — это первый в истории техники способ двоичного кодирования, информации. Благодаря этой идее удалось создать буквопечатающий телеграфный аппарат, имеющий вид пишущей машинки. Нажатие на клавишу с определенной буквой вырабатывает соответствующий пятиимпульсный сигнал, который передаетсяпо линии связи.
В честь Бодо была названа единица скорости передачи информации — бод.
В современных компьютерах для кодирования текста также применяется равномерный двоичный код.
Telex
Это интересно:
Отель, не имеющий телекса, не может иметь рейтинг "пять звезд".
Слайд 10Двоичное кодирование в компьютере
Вся информация, которую обрабатывает компьютер должна быть
представлена двоичным кодом с помощью двух цифр: 0 и 1.
Эти два символа принято называть двоичными цифрами или битами.С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Слайд 11Двоичное кодирование — это кодирование информации при помощи нулей и единиц.
Эти знаки называются двоичными цифрами, по-английски — binary digit или
сокращенно bit (бит). Слайд 12Почему двоичное кодирование
С точки зрения технической реализации использование двоичной системы
счисления для кодирования информации оказалось намного более простым, чем применение
других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:0 – отсутствие электрического сигнала;
1 – наличие электрического сигнала.
Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
Слайд 14Для работы с числами человек использует в основном две формы
для их записи – естественную и экспоненциальную.
Экспоненциальная форма записи чисел
используется для обозначения очень больших или очень маленьких чисел.Например 0,000002=0,2*10-5 или 1000=103.
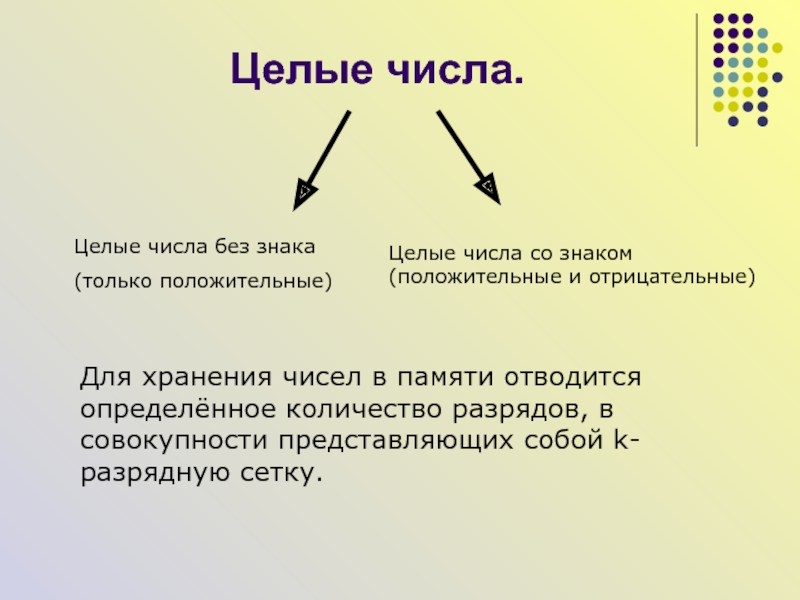
Слайд 15Целые числа.
Целые числа без знака
(только положительные)
Целые числа со знаком
(положительные и отрицательные)
Для хранения чисел в памяти отводится определённое количество
разрядов, в совокупности представляющих собой k-разрядную сетку.Слайд 16Представление целых чисел
Ячейка - объем памяти, предоставленный для хранения одного
числа.
Память дискретна и адресуема.
Каждое число хранится в определенной ячейке
памяти.Байты памяти нумеруются (адрес ячейки).
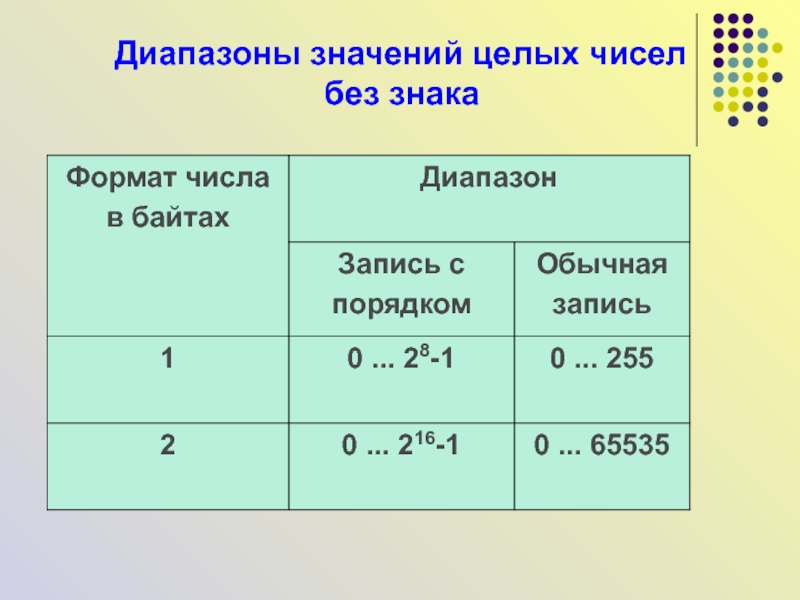
Слайд 17Как представляются в компьютере целые числа?
Целые числа могут
представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112 , а в двубайтовом формате - от 00000000 000000002 до 11111111111111112.Слайд 19Число 3910 = 100111 2 в однобайтовом формате:
Число 3910 =
100111 2 в двубайтовом формате:
Число 65 53510 = 11111111 111111112
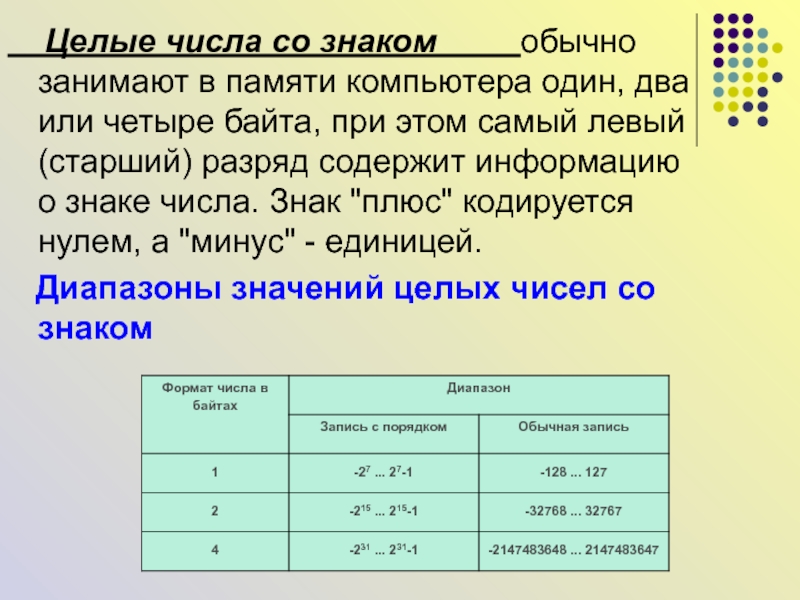
в двубайтовом формате:Слайд 20 Целые числа со знаком
обычно занимают в памяти компьютера один, два или четыре байта,
при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак "плюс" кодируется нулем, а "минус" - единицей.Диапазоны значений целых чисел со знаком
Слайд 21Целые числа со знаком.
В компьютерной технике применяются три формы записи
(кодирования) целых отрицательных чисел: прямой код, обратный код, дополнительный код.
Слайд 22 Положительные числа в прямом, обратном и дополнительном кодах изображаются
одинаково - двоичными кодами с цифрой 0 в знаковом разряде.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа - двоичный код его абсолютной величины
Слайд 23 2. Обратный код. Получается инвертированием всех цифр двоичного
кода абсолютной величины числа, включая разряд знака: нули заменяются единицами,
а единицы –нулями.3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Слайд 24Прямой код числа.
В знаковый разряд помещается цифра 1, а в
разряды цифровой части – двоичный код его абсолютной величины.
Пример
Прямой
код числа -1:Знак числа «-»
Слайд 25Обратный код числа.
Получается инвертированием всех цифр двоичного кода абсолютной величины
числа, включая разряд знака: нули заменяются единицами, а единицы –
нулями.Пример
Число: -1.
Код модуля числа: 0 0000001.
Обратный код числа: 1 1111110.
Слайд 26Дополнительный код числа.
Получается образованием обратного кода с последующем прибавлением единицы
к его младшему разряду.
Пример
Число: -1.
Код модуля числа: 0
0000001.Обратный код числа: 1 1111110
+1
1 1111111
Слайд 27Представление целых отрицательных чисел
Отрицательные числа в памяти компьютера записываются с
помощью дополнительного кода.
Записать представление положительного числа.
Инвертировать код.
К инвертированному числу
прибавить 1.ПРОВЕРИТЬ: при сложении с положительным числом получаем 0.
Слайд 31 Сложение
0+0=0
0+1=1
1+0=1
1+1=10
1101+110 =
10011
1 1 0 1
1 1 0
+
1 + 1
+ 1 = ?
1 + 1 = 10
10 + 1
= 1110
+ 1
_____________
11
0
1
1
1
0
1
Слайд 34В большинстве компьютеров операция вычитание не используется. Вместо неё производится
сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет
существенно упростить конструкцию АЛУ. Вычитание
100000-11=11101
Решение:
Слайд 35 Деление выполняется по правилам математики, не забывая, что мы
выполняем действия в двоичной системе счисления.
101010:111=110
Решение:
Любые машинные вычисления содержат погрешность.
Поэтому корень из числа 4 вполне может быть равен 1,9974. Деление
Слайд 37 1. А и В положительные. При суммировании складываются
все разряды, включая разряд знака. Так как знаковые разряды положительных
слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:Получен правильный результат.
Слайд 38 2. А положительное, B отрицательное и по абсолютной
величине больше, чем А.
Например:
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –710. Слайд 39 3. А положительное, B отрицательное и по абсолютной
величине меньше, чем А. Например:
Компьютер исправляет полученный
первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы!!! Слайд 40 4. А и В отрицательные. Например:
Полученный первоначально неправильный результат (обратный код числа –1110 вместо обратного
кода числа –1010) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –1010.
Слайд 41 5. А и В положительные, сумма А+В больше,
либо равна 2n–1, где n – количество разрядов формата чисел
(для однобайтового формата n=8, 2n–1 = 27 = 128). Например:Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (16210 = 101000102), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых (знак суммы – отрицателен, знак слагаемых – положительный), что является свидетельством переполнения разрядной сетки.
Слайд 426. А и В отрицательные, сумма абсолютных величин А и
В больше, либо равна 2n–1.
Например:
632 =01111112
Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.
Слайд 431. А и В положительные. Здесь нет отличий от случая
1, рассмотренного для обратного кода, т.к. дополнительный код используется только
для отрицательных чисел.Слайд 44 2. А положительное, B отрицательное и по абсолютной величине
больше, чем А. Например:
Получен правильный результат
в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –710.
Слайд 45 3. А положительное, B отрицательное и по абсолютной
величине меньше, чем А.
Например:
Получен правильный результат.
Единицу переноса из знакового разряда компьютер отбрасывает. Слайд 46 4. А и В отрицательные.
Например:
Получен правильный результат в дополнительном коде. Единицу переноса из
знакового разряда компьютер отбрасывает. Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.Слайд 47Что такое переполнение?
Выход результатов вычислений за границы допустимого диапазона называется
переполнением.
Переполнение приводит к ошибкам при автоматических расчетах или остановке выполнения
программы.Программист должен правильно определять тип данных (диапазон чисел).
Слайд 49Представление чисел с плавающей точкой.
Этот способ представления
опирается на нормализованную (экспоненциальную) запись действительных чисел. Нормализованная запись отличного
от нуля действительного числа A - это запись вида: А= m* qn, где m – мантисса числа (правильная дробь, у которой первая цифра после запятой не равна нулю), q – основание системы, n – порядок числа.Слайд 50Например, число 25,324 можно записать в таком виде: 0.25324х102.
Здесь
m=0.25324 — мантисса,
n=2 — порядок. Порядок указывает, на какое
количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».Однако справедливы и следующие равенства:
25,324 = 2,5324*101 = 0,0025324*104 = 2532,4*102 и т.п.
Слайд 51Получается, что представление числа в форме с плавающей точкой неоднозначно?
Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа
в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию:0,1p ≤ m < 1p.
Слайд 52Иначе говоря, мантисса меньше единицы и первая значащая цифра —
не ноль. Значит для рассмотренного числа нормализованным представлением будет: 25,324=0.25324
* 102.Слайд 53Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют
формат с плавающей точкой (запятой).
Форма с плавающей точкой использует представление
вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:R = m * рn
m – мантисса,
n – порядок,
p – основание системы.
Слайд 54Пусть в памяти компьютера вещественное число представляется в форме с
плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку
размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке:1-й байт 2-й байт 3-й байт 4-й байт
В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.
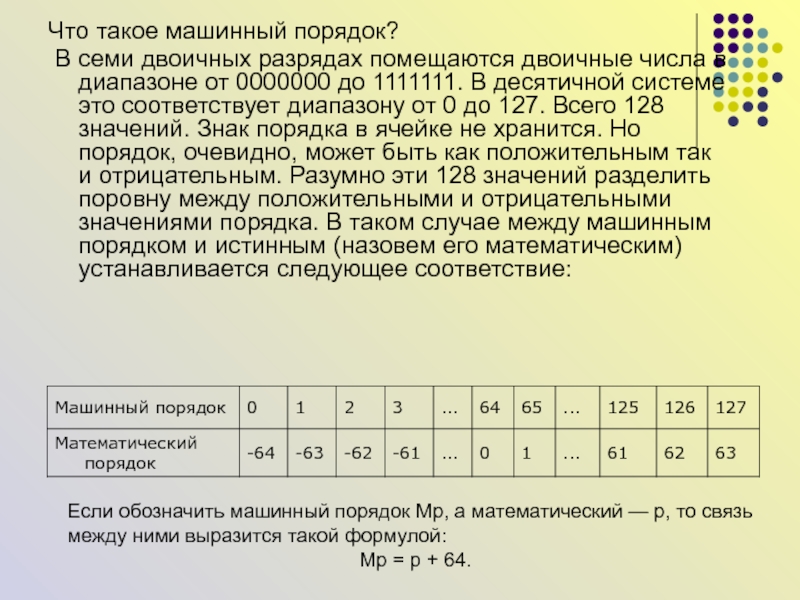
Слайд 55Что такое машинный порядок?
В семи двоичных разрядах помещаются двоичные
числа в диапазоне от 0000000 до 1111111. В десятичной системе
это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:Если обозначить машинный порядок Мр, а математический — р, то связь между ними выразится такой формулой:
Мр = р + 64.
Слайд 56Итак, машинный порядок смещён относительно математического на 64 единицы и
имеет только положительные значения. При выполнении вычислений с плавающей точкой
процессор это смещение учитывает.В двоичной системе счисления смещение:
Мр2 = р2+100 00002
Слайд 57Теперь мы можем записать внутреннее представление числа 25,324 в форме
с плавающей точкой.
1)Переведем его в двоичную систему счисления с
24 значащими цифрами. 25,32410= 11001,01010010111100011012
2)Запишем в форме нормализованного двоичного числа с плавающей точкой:
0,110010101001011110001101*10101
Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе.
3) Вычислим машинный порядок.
Мр2 = 101 + 100 0000 = 100 0101.
4) Запишем представление числа в ячейке памяти.
Знак числа
порядок
мантисса
31
0
Слайд 58Число в форме с плавающей точкой занимает в памяти компьютера
4 байта (число обычной точности) или 8 байт (число двойной
точности).Мы рассмотрели пример представления числа 25,324 обычной точности