Слайд 1Представление числовой информации
в компьютере
Решение задач
Презентация 10-10
Слайд 2Форматы представления чисел
целочисленный
с плавающей точкой
целые неотрицательные числа
целые числа
со знаком
Слайд 3Формат с плавающей точкой используется для представления в компьютере действительных
чисел (англ. real).
Представление числа в плавающей форме не является единственным:
3
• 108 = 30 • 107 = 0,3 • 109 = 0,03 • 1010 = ...
Договорились для выделения единственного варианта записи числа считать, что целая часть числа отсутствует, а первый разряд содержит отличную от нуля цифру .
Т.е. обоим требованиям удовлетворит только число 0,3 • 109
Слайд 4Вещественное число представляется в виде произведения мантиссы (m) и основания
системы счисления в целой степени (n), называемой порядком.
R =
m * Рn .
Порядок n указывает, на какое количество позиций и в каком направлении должна сместиться в мантиссе точка (запятая), отделяющая дробную часть от целой. Мантисса нормализуется, т. е. представляется в виде правильной дроби (0 < m < 1).
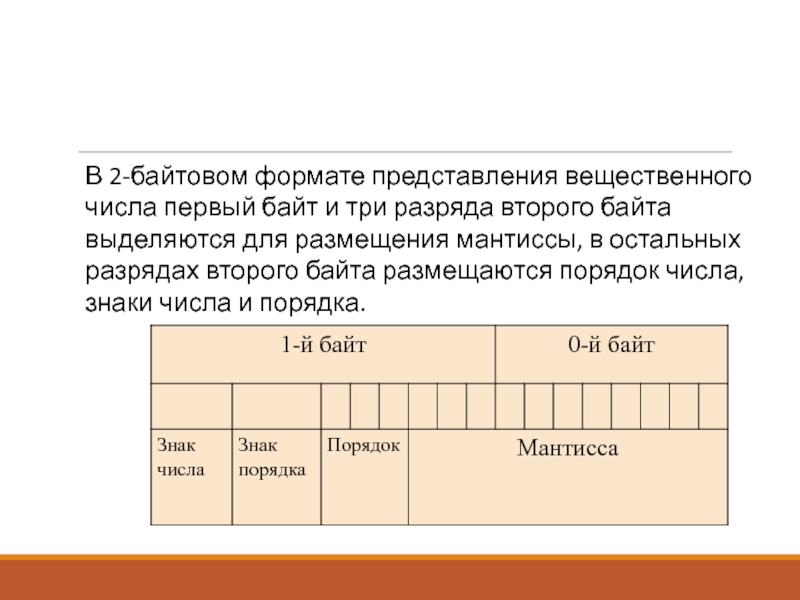
Слайд 5В 2-байтовом формате представления вещественного числа первый байт и три
разряда второго байта выделяются для размещения мантиссы, в остальных разрядах
второго байта размещаются порядок числа, знаки числа и порядка.
Слайд 6В 4-байтовом формате представления вещественного числа первые три байта выделяются
для размещения мантиссы, в четвертом байте размещаются порядок числа, знаки
числа и порядка.
Слайд 7Задание
1. Переведите число В0С16 в двоичную систему счисления.
2. Переведите в шестнадцатеричную
систему счисления двоичное число 101011.
3. Дано А = A716, B
= 2518. Найдите сумму A + B. Ответ укажите в двоичной системе.
4. Чему равна сумма чисел 305 и 418? Результат запишите в двоичной системе счисления.
5. Вычислите сумму чисел х и у при x = B316, у = 1101102. Результат представьте в десятичной системе счисления.
Слайд 8Задание
6. Укажите наибольшее десятичное число, которое в двоичной системе счисления
можно записать с помощью трёх цифр.
Ответ: 7.
7. Даны 4 целых числа,
записанных в шестнадцатеричной системе: A8, AB, B5, CA. Сколько среди них чисел, больших, чем 2658?
Ответ: 1.
Слайд 9Задание
8. Для передачи по каналу связи сообщения, состоящего только из
символов А, Б, В и Г, используется посимвольное кодирование: А-00,
Б-11, В-010, Г-011. Через канал связи передаётся сообщение: ВБГАГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
Ответ: 5В1А.
Слайд 10Задание
9. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит
5 единиц. В ответе запишите только само восьмеричное число, основание
системы счисления указывать не нужно.
Ответ: 1017.
Слайд 11Задание
10. Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит
ровно 6 нулей. В ответе запишите только само шестнадцатеричное число,
основание системы счисления указывать не нужно.
Пояснение.
Четырёхзначное, значит, в двоичной записи оно не меньше 100016 =
=1 0000 0000 00002. Чем старше разряд, тем больше он прибавляет к числу. Поэтому нули стоит ставить именно в старшие разряды. Итого получим 1 0000 0011 11112 = 103F16.
Примечание. Число 81F не подходит, так как необходимо найти четырёхзначное шестнадцатеричное число.
Ответ: 103F.
Слайд 12Задание
11. Сколько существует натуральных чисел x, для которых выполняется неравенство
101101112 < x < 101111112?
В ответе укажите только количество чисел, сами
числа писать не нужно.
Ответ: 7.
Слайд 13Задание
12. Для кодирования букв О, В, Д, П, А решили
использовать двоичное представление чисел 0, 1, 2, 3 и 4
соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
Ответ: 22162.
Слайд 14Задание
13. Все 5-буквенные слова, составленные из букв Л, Н, Р,
Т, записаны в алфавитном порядке. Вот начало списка:
1. ЛЛЛЛЛ
2. ЛЛЛЛН
3.
ЛЛЛЛР
4. ЛЛЛЛТ
5. ЛЛЛНЛ
Запишите слово, которое стоит на 150-м месте от начала списка.
Ответ: ЛРННН.
Слайд 15Задание
14. Все 5-буквенные слова, составленные из букв А, Н, П,
записаны в алфавитном порядке.
Вот начало списка:
1. ААААА
2. ААААН
3. ААААП
4. АААНА
5.
АААНН
Запишите слово, которое стоит на 201-м месте от начала списка.
Ответ: ПННАП
Слайд 16Задание
15. В системе счисления с некоторым основанием десятичное число 18
записывается в виде 30. Укажите это основание.
Ответ: 6.
16. В системе
счисления с основанием N запись числа 4110 оканчивается на 2, а запись числа 13110 — на 1. Чему равно число N?
Ответ: 13.
Слайд 17Задание
17. Укажите, сколько всего раз встречается цифра 2 в записи
чисел 10, 11, 12, …, 17 в системе счисления с
основанием 5.
Ответ: Всего цифра «2» встречается 7 раз.
18. Решите уравнение: 101x + 1310 = 101х+1
Ответ: Х=6.
19. Решите уравнение: 356 + x = 357
Ответ запишите в десятичной системе счисления.
Ответ: 3.
Слайд 18Домашнее задание
Задания из презентаций 10-10
Самостоятельная работа
Слайд 19Домашнее задание
1. Переведите в восьмеричную систему счисления двоичное число 110110.
Ответ:
66.
2. Вычислите сумму чисел x и у при х =
7710, у = 778. Результат представьте в двоичной системе счисления.
Ответ: 100011002.
Слайд 20Домашнее задание
3. Сколько верных неравенств среди перечисленных:
100110102 > 25610;
100110102 > 9F16;
100110102 > 2328.
Ответ: 0.
4.
Сколько существует натуральных чисел x, для которых выполнено неравенство 110111002
ответе укажите только количество чисел, сами числа писать не нужно.
Ответ: 2.
Слайд 21Домашнее задание
5. Сколько существует целых чисел x, для которых выполняется
неравенство 2A16
писать не нужно.
Ответ: 6.
6. Для кодирования букв Д, X, Р, О, В решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Закодируйте последовательность букв ХОРОВОД таким способом и результат запишите восьмеричным кодом.
Ответ: 36714.
Слайд 22Домашнее задание
7. Для передачи по каналу связи сообщения, состоящего только
из символов А, Б, В и Г, используется неравномерный (по
длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.
Ответ: 151646.
8. В системе счисления с основанием N запись числа 7910 оканчивается на 2, а запись числа 11110 — на 1. Чему равно число N?
Ответ: 11.
Слайд 23Домашнее задание
9. Решите уравнение 121x + 110 = 1019.
Ответ: 8.