Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование Хафа
Содержание
- 1. Преобразование Хафа
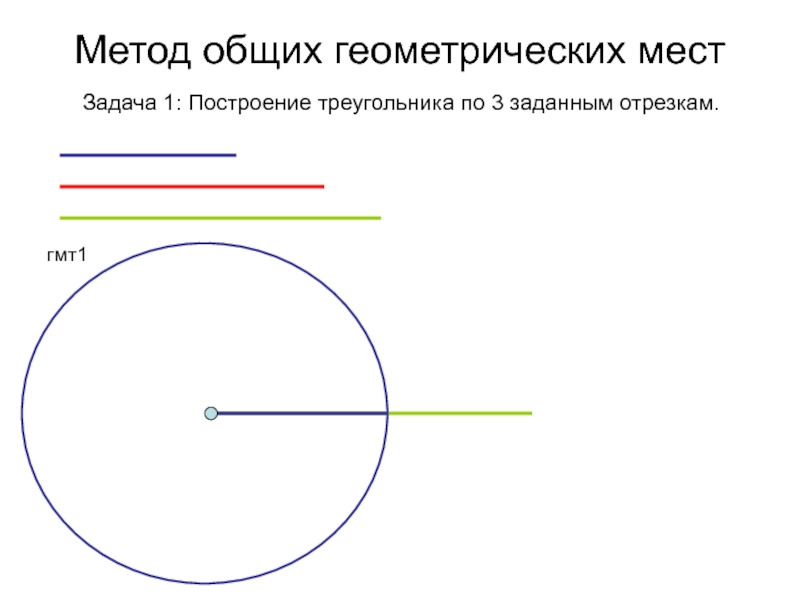
- 2. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.
- 3. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1
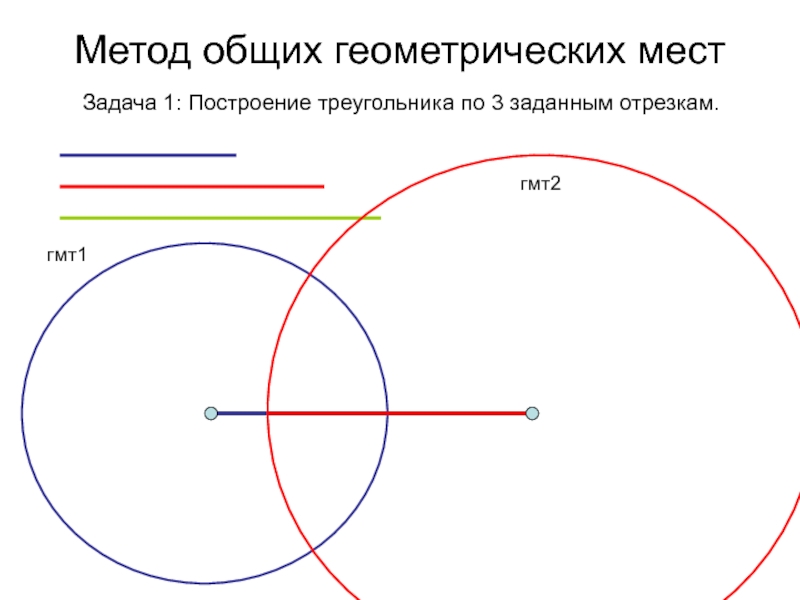
- 4. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1гмт2
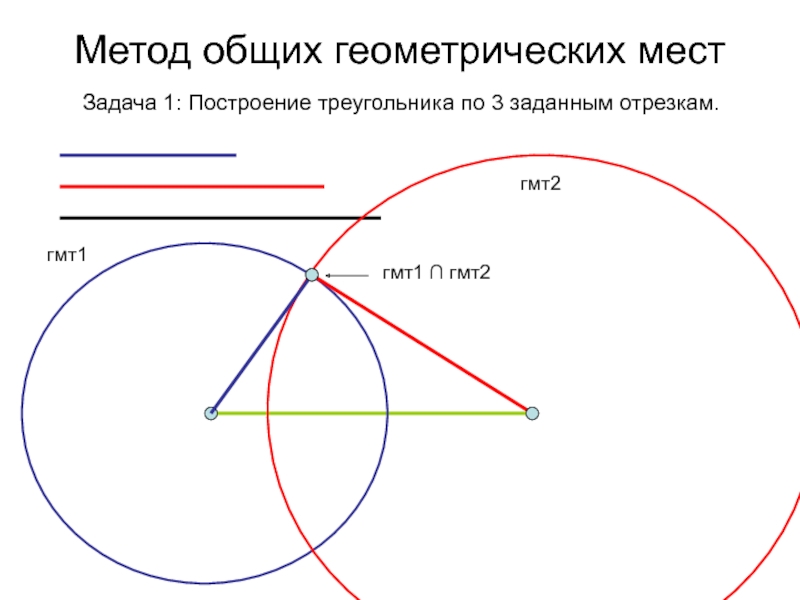
- 5. Метод общих геометрических мест Задача 1: Построение треугольника по 3 заданным отрезкам.гмт1гмт2гмт1 ∩ гмт2
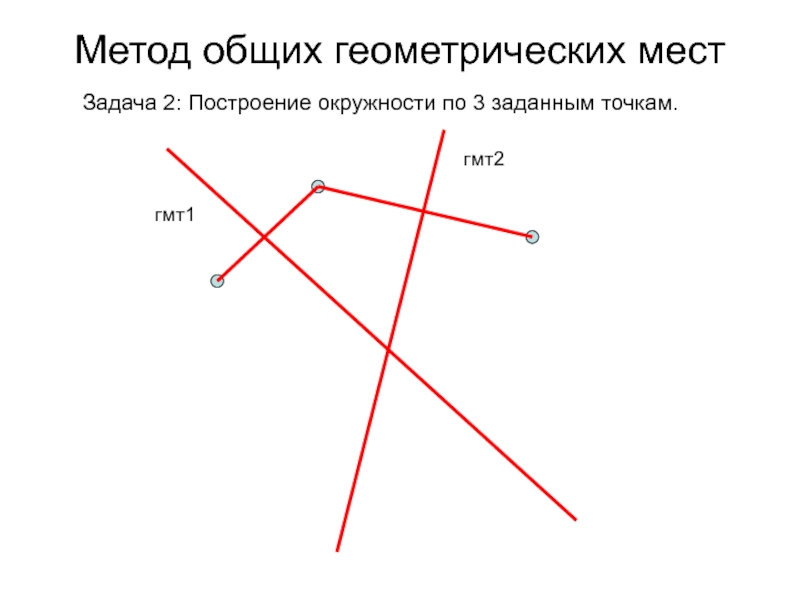
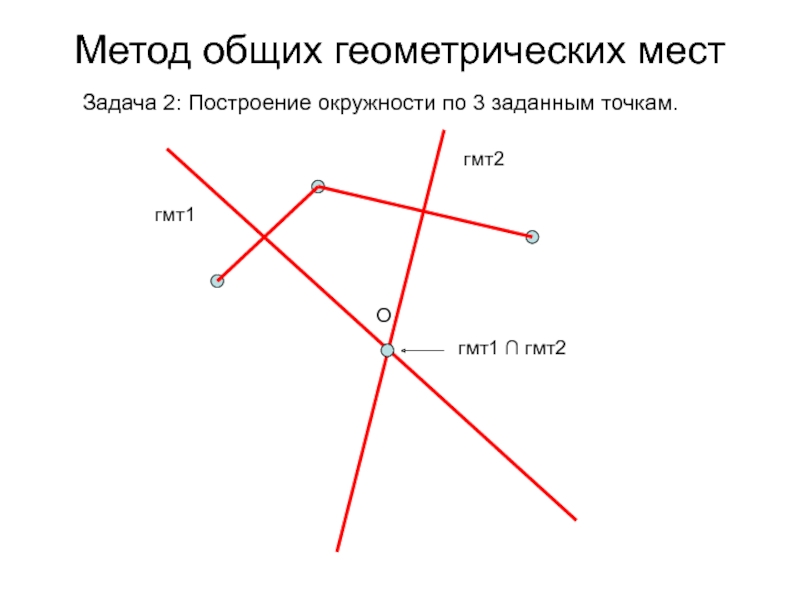
- 6. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.
- 7. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1
- 8. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2
- 9. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2O
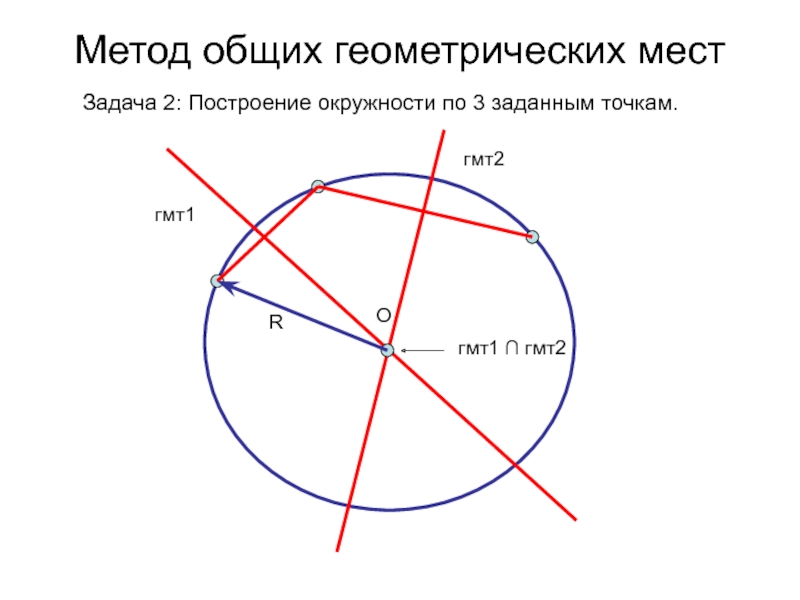
- 10. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2RO
- 11. Метод общих геометрических мест Задача 2: Построение окружности по 3 заданным точкам.гмт1гмт2гмт1 ∩ гмт2RO
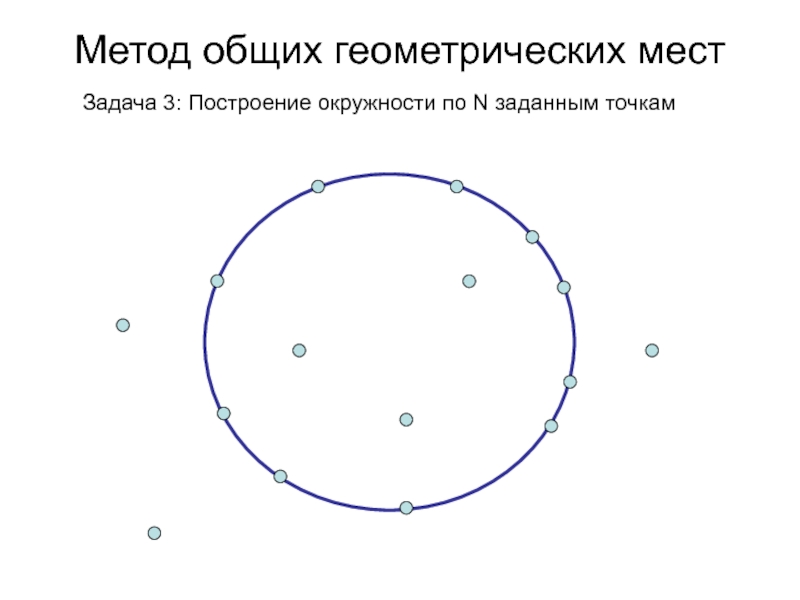
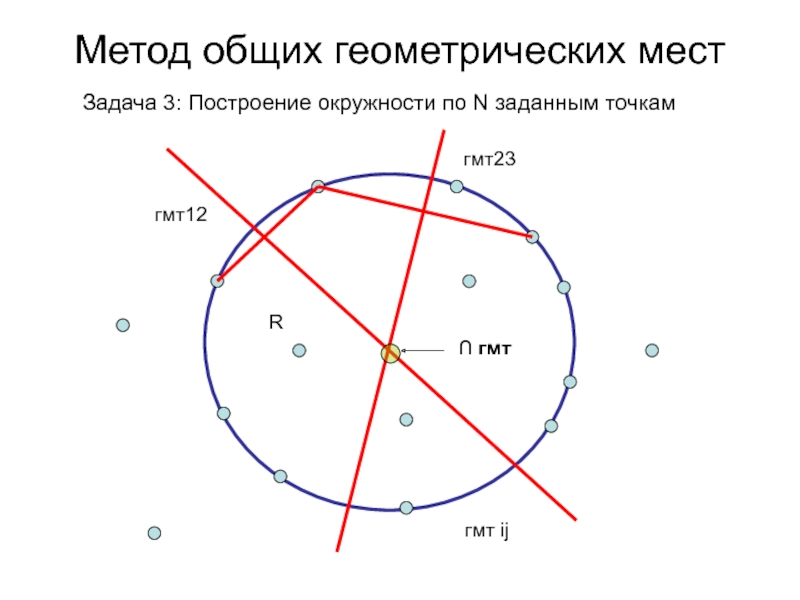
- 12. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкам
- 13. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкам
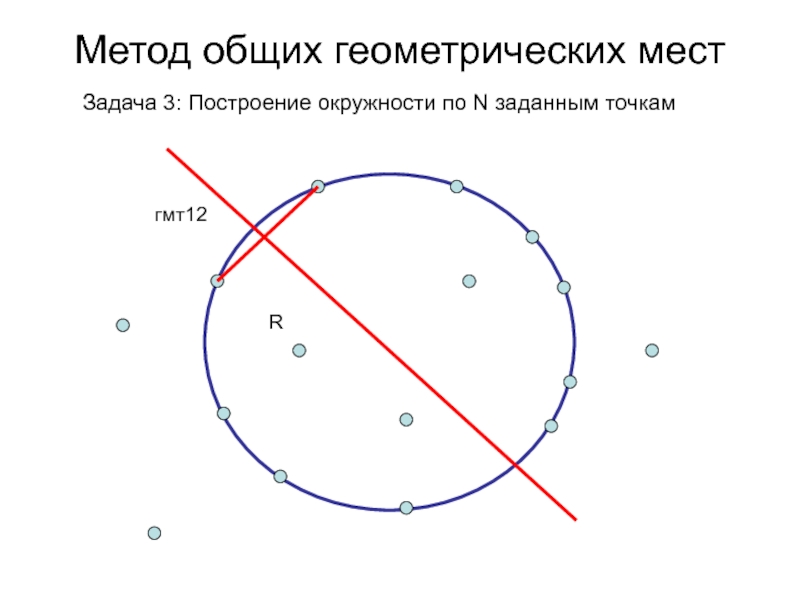
- 14. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12R
- 15. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23∩ гмтRгмт ij
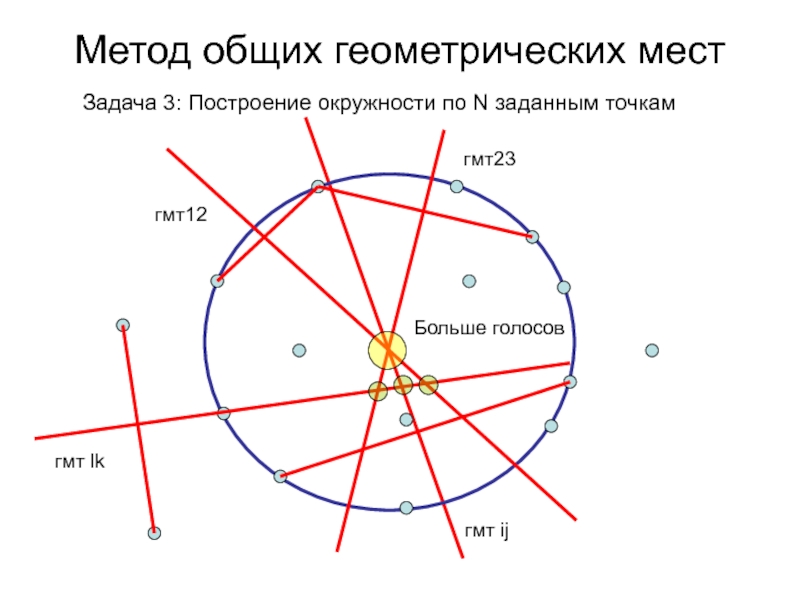
- 16. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23гмт lk
- 17. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23гмт ijгмт lkБольше голосов
- 18. Метод общих геометрических мест Задача 3: Построение окружности по N заданным точкамгмт12гмт23MAX ∩ гмтROгмт ijгмт lk
- 19. Преобразование Хафа (Hough) Преобразование Хафа позволяет находить на
- 20. Основная идея метода Рассмотрим семейство кривых на плоскости,
- 21. Машинное представление Ввиду дискретности машинного представления и входных
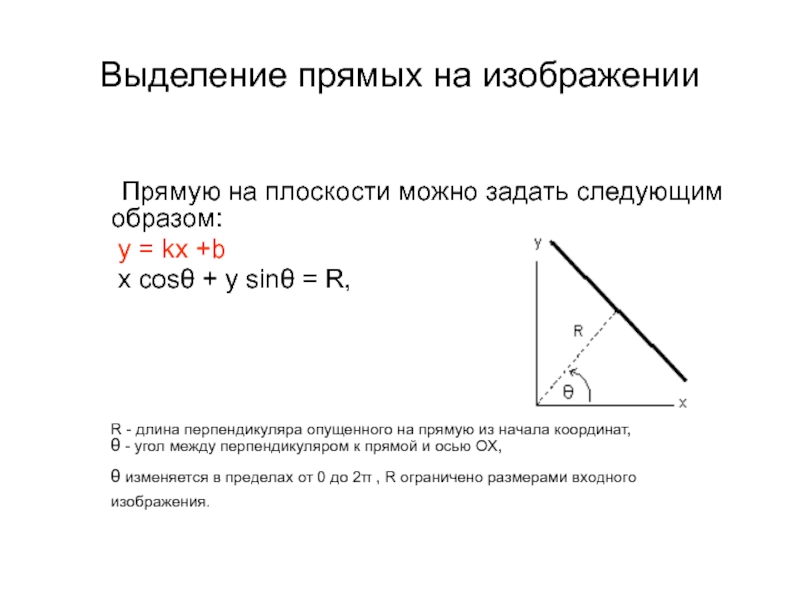
- 22. Выделение прямых на изображении Прямую на плоскости можно
- 23. Выделение прямых на изображении Таким образом функция, задающая
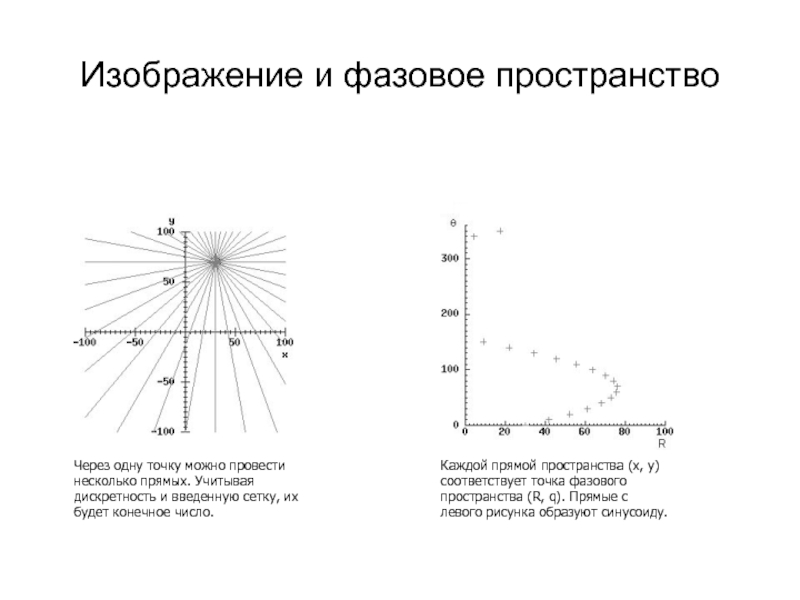
- 24. Изображение и фазовое пространствоЧерез одну точку можно
- 25. Изображение и фазовое пространствоИзображение с пятью точками
- 26. Дискретизация фазового пространстваПереводим непрерывное фазовое пространство в
- 27. Алгоритм выделения прямыхобнулить счетчики всех ячеек;для каждой
- 28. Размер ячеек стоит выбирать аккуратно Если ячейки будут
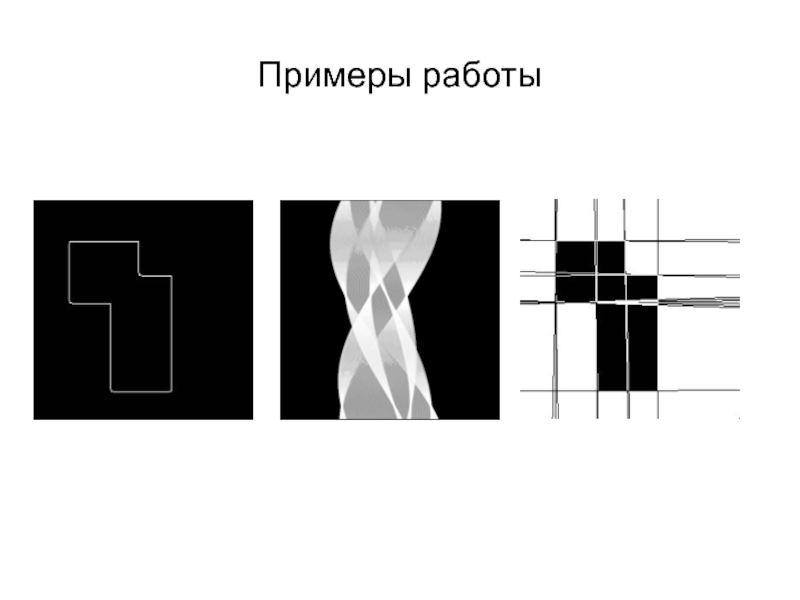
- 29. Примеры работы
- 30. Примеры работы (с шумом)
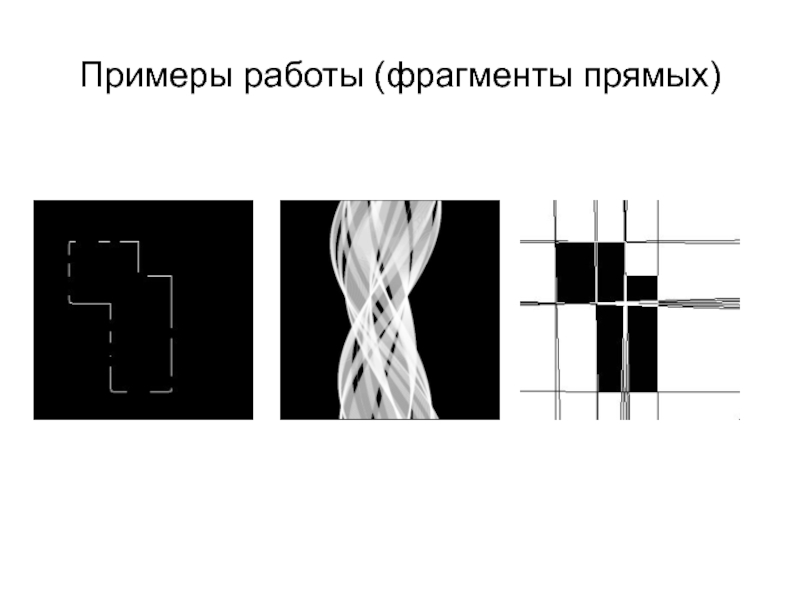
- 31. Примеры работы (фрагменты прямых)
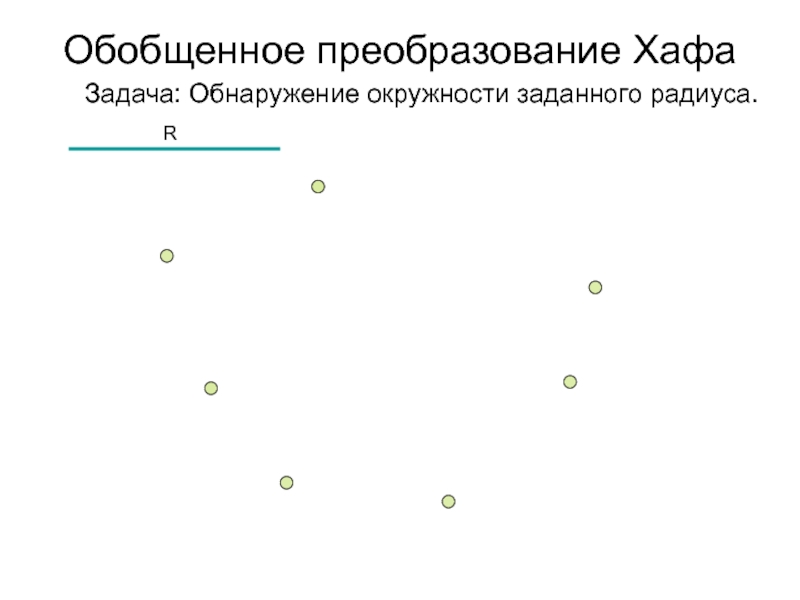
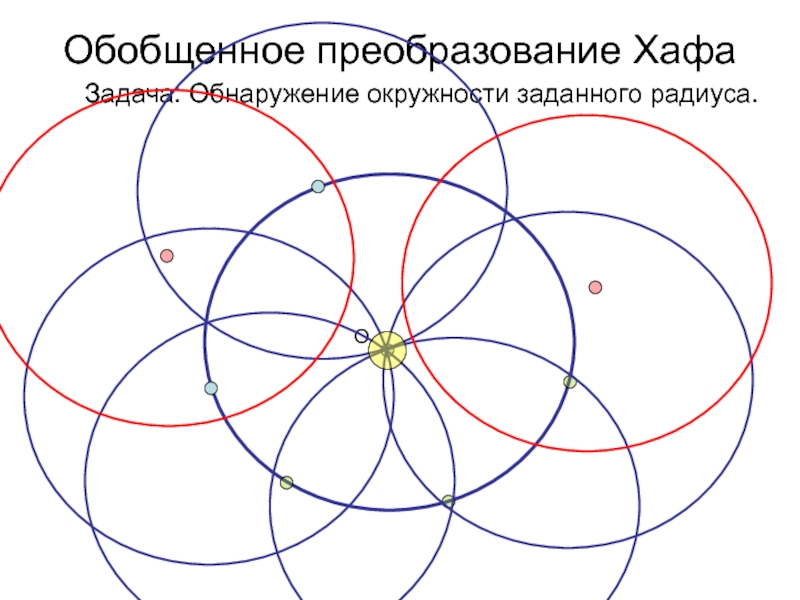
- 32. Обобщенное преобразование Хафа Задача: Обнаружение окружности заданного радиуса.R
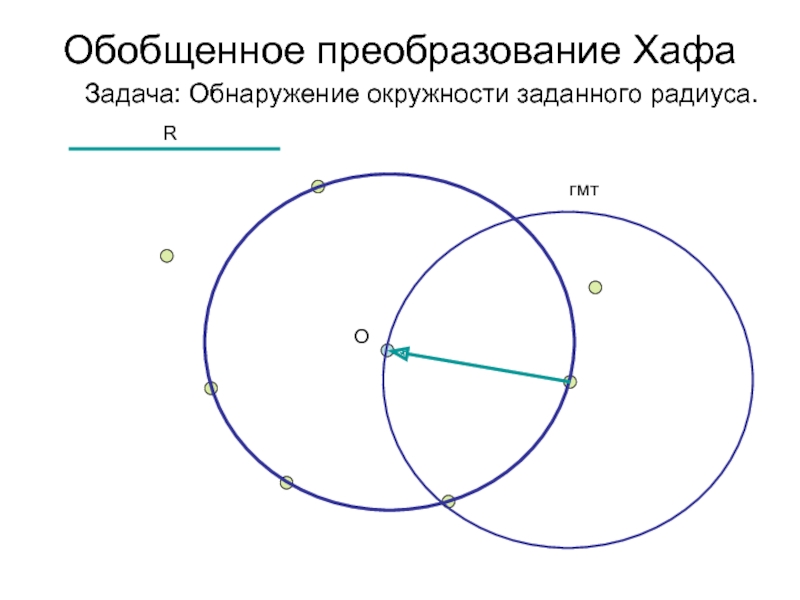
- 33. Обобщенное преобразование Хафа Задача: Обнаружение окружности заданного радиуса.ROгмт
- 34. Обобщенное преобразование Хафа Задача: Обнаружение окружности заданного радиуса.O
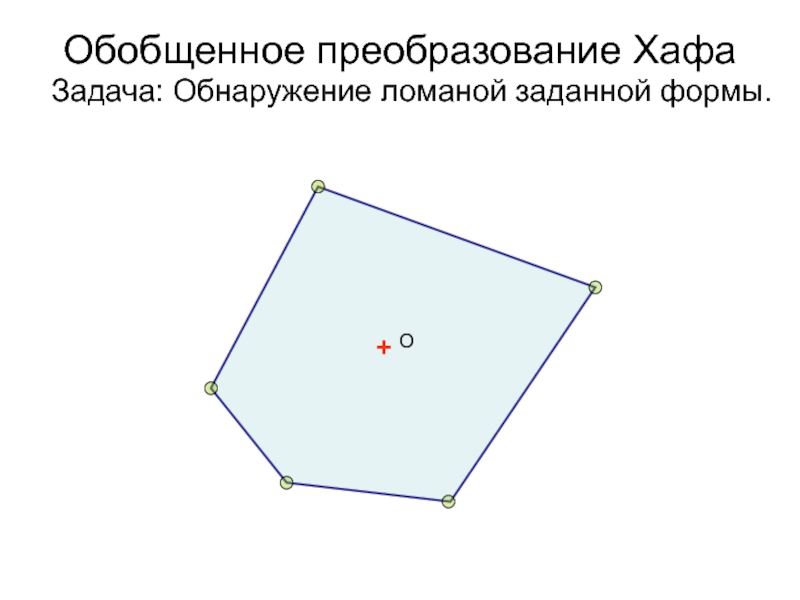
- 35. Обобщенное преобразование Хафа Задача: Обнаружение ломаной заданной формы.+ О
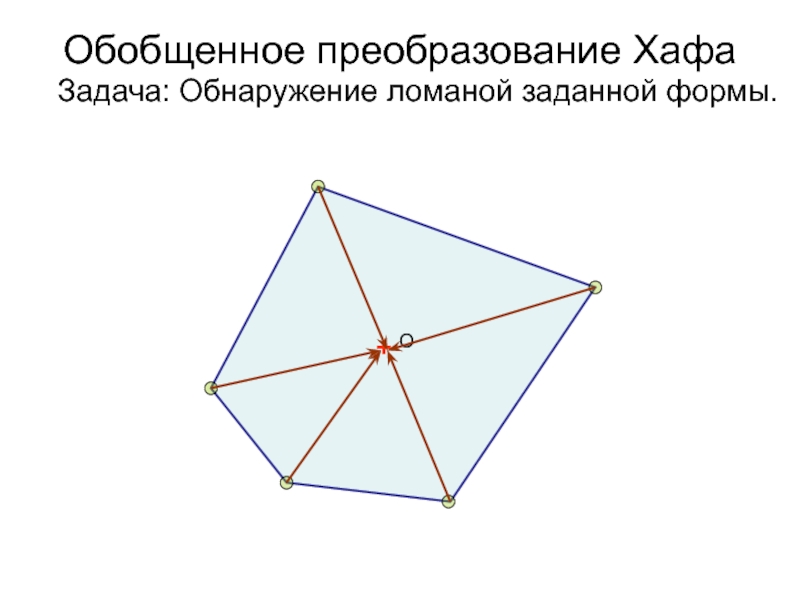
- 36. Обобщенное преобразование Хафа Задача: Обнаружение ломаной заданной формы.+ О
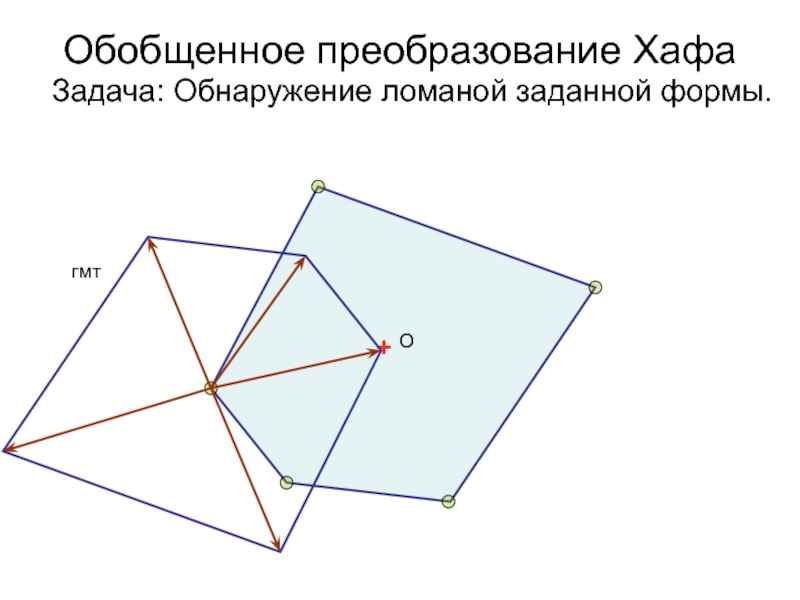
- 37. Обобщенное преобразование Хафа Задача: Обнаружение ломаной заданной формы.+ Огмт
- 38. Обобщенное преобразование Хафа Задача: Обнаружение ломаной заданной формы.+ ОLUT
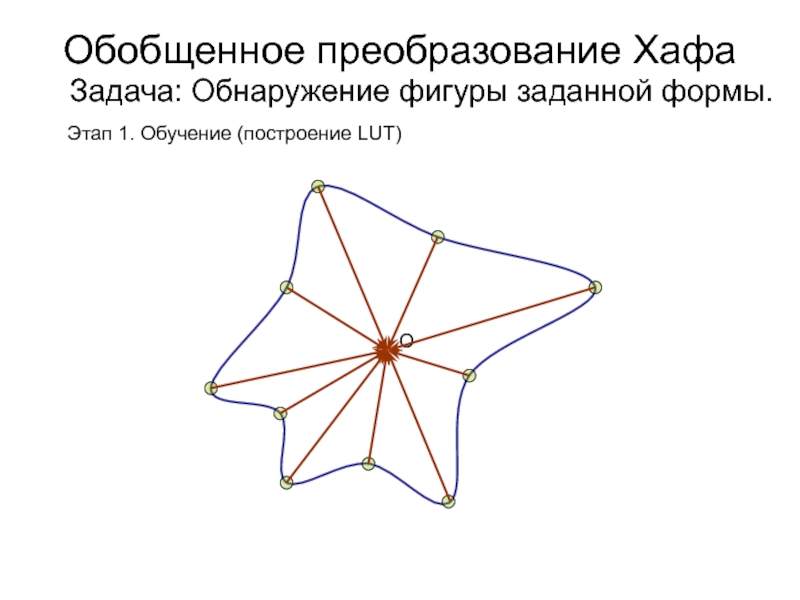
- 39. Обобщенное преобразование Хафа Задача: Обнаружение фигуры заданной формы.+ ОЭтап 1. Обучение (построение LUT)
- 40. Обобщенное преобразование Хафа Задача: Обнаружение фигуры заданной формы.+ ОЭтап 1. Обучение (построение LUT)
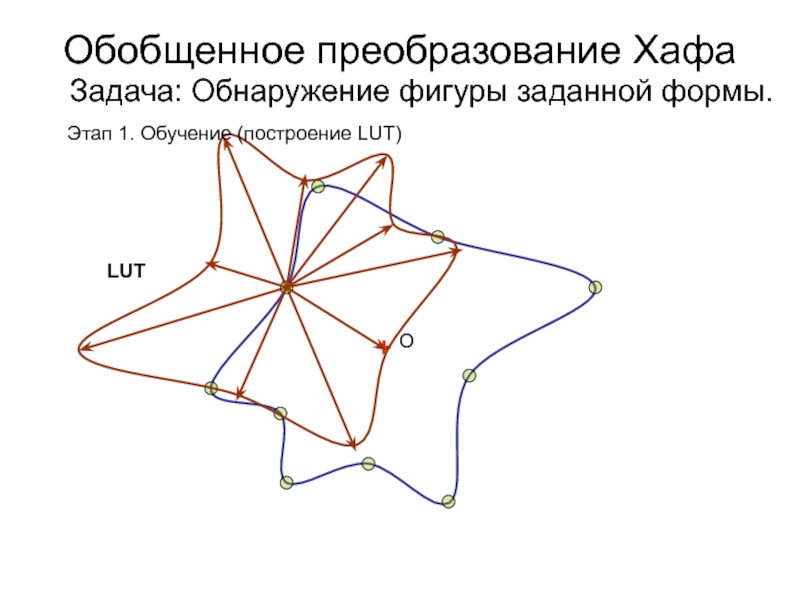
- 41. Обобщенное преобразование Хафа Задача: Обнаружение фигуры заданной формы.+ ОLUTЭтап 1. Обучение (построение LUT)
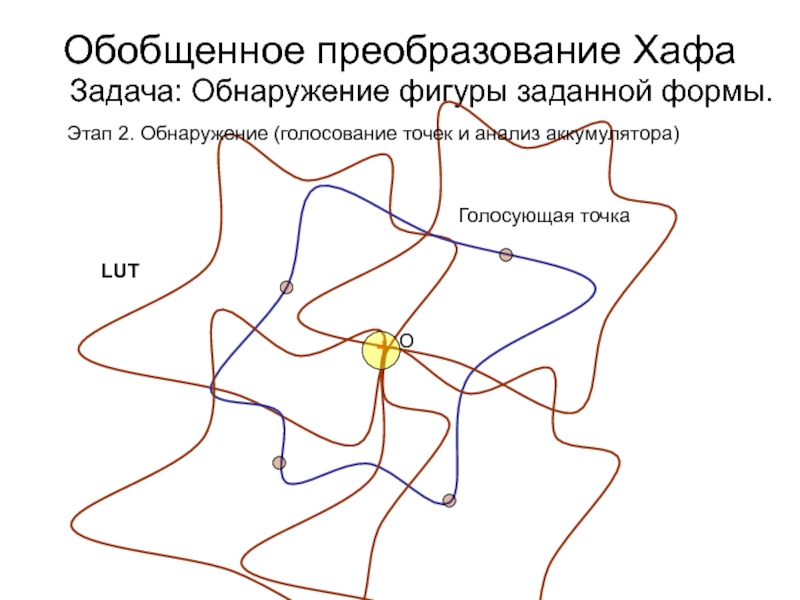
- 42. Обобщенное преобразование Хафа Задача: Обнаружение фигуры заданной формы.+ ОLUTГолосующая точкаЭтап 2. Обнаружение (голосование точек и анализ аккумулятора)
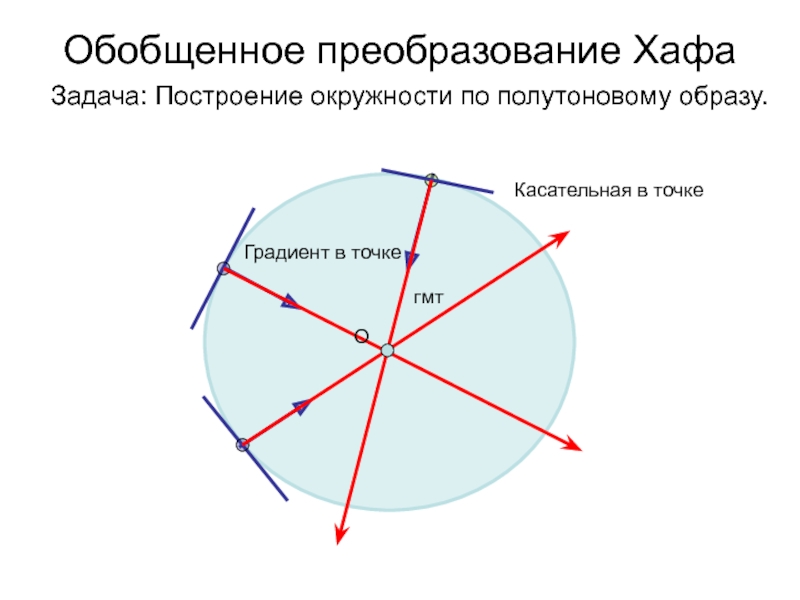
- 43. Обобщенное преобразование Хафа Задача: Построение окружности по полутоновому образу.гмтOКасательная в точкеРадиус-вектор в точкеГрадиент в точке
- 44. Обобщенное преобразование ХафагмтКасательная в точкеOГрадиент в точке Задача: Построение окружности по полутоновому образу.
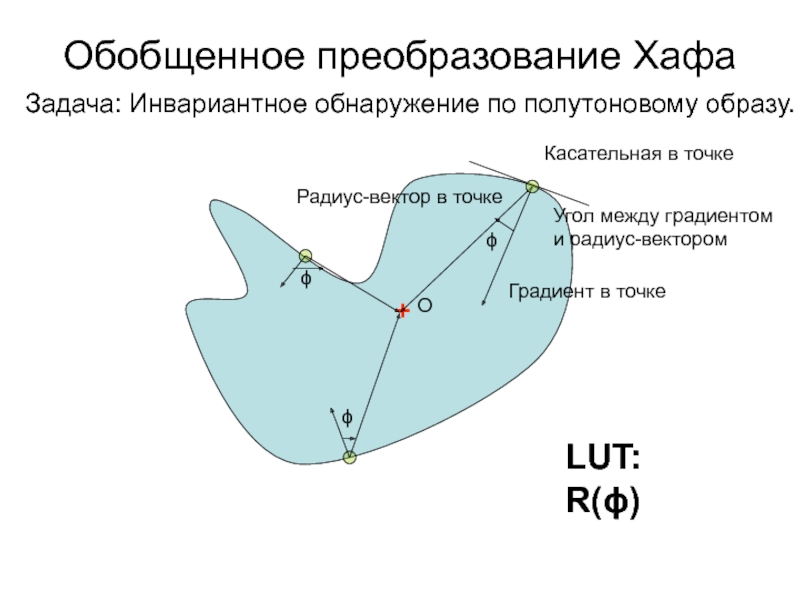
- 45. Обобщенное преобразование Хафа Задача: Инвариантное обнаружение по полутоновому образу.
- 46. Обобщенное преобразование Хафа+ О Задача: Инвариантное обнаружение по полутоновому образу.
- 47. Обобщенное преобразование Хафа+ ОКасательная в точкеГрадиент в
- 48. Обобщенное преобразование Хафа+ ОКасательная в точкеГрадиент в
- 49. Морфологии Серра на базе преобразования Хафа
- 50. Морфологии Серра на базе преобразования ХафаМонотонная морфология
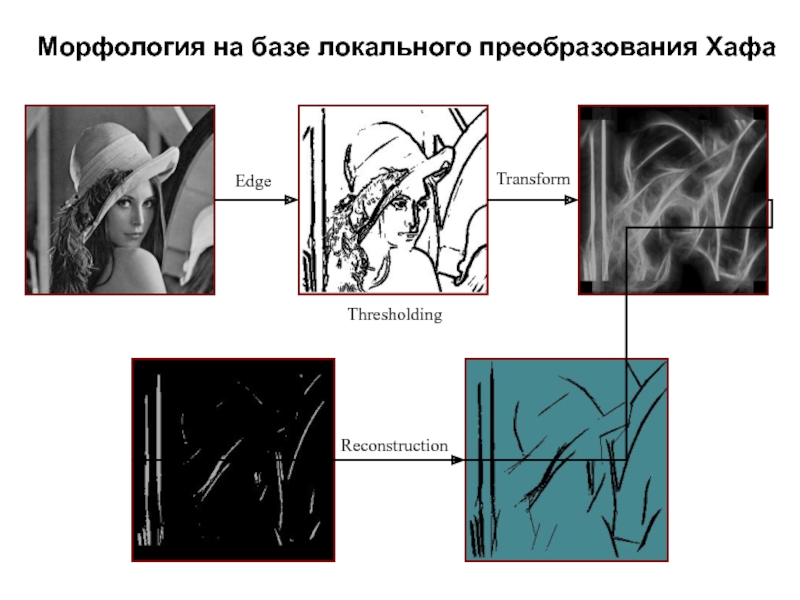
- 51. Морфология на базе локального преобразования ХафаTransformThresholdingReconstructionEdge
- 52. Морфология на базе локального преобразования ХафаTransformThresholdingReconstructionEdge
- 53. Выделение линеаментов различных размеров
- 54. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Метод общих геометрических мест
Задача 1: Построение треугольника по 3 заданным
отрезкам.
гмт1
Слайд 4Метод общих геометрических мест
Задача 1: Построение треугольника по 3 заданным
отрезкам.
гмт1
гмт2
Слайд 5Метод общих геометрических мест
Задача 1: Построение треугольника по 3 заданным
отрезкам.
гмт1
гмт2
гмт1 ∩ гмт2
Слайд 8Метод общих геометрических мест
Задача 2: Построение окружности по 3 заданным
точкам.
гмт1
гмт2
Слайд 9Метод общих геометрических мест
Задача 2: Построение окружности по 3 заданным
точкам.
гмт1
гмт2
гмт1 ∩ гмт2
O
Слайд 10Метод общих геометрических мест
Задача 2: Построение окружности по 3 заданным
точкам.
гмт1
гмт2
гмт1 ∩ гмт2
R
O
Слайд 11Метод общих геометрических мест
Задача 2: Построение окружности по 3 заданным
точкам.
гмт1
гмт2
гмт1 ∩ гмт2
R
O
Слайд 15Метод общих геометрических мест
Задача 3: Построение окружности по N заданным
точкам
гмт12
гмт23
∩ гмт
R
гмт ij
Слайд 16Метод общих геометрических мест
Задача 3: Построение окружности по N заданным
точкам
гмт12
гмт23
гмт lk
Слайд 17Метод общих геометрических мест
Задача 3: Построение окружности по N заданным
точкам
гмт12
гмт23
гмт ij
гмт lk
Больше голосов
Слайд 18Метод общих геометрических мест
Задача 3: Построение окружности по N заданным
точкам
гмт12
гмт23
MAX ∩ гмт
R
O
гмт ij
гмт lk
Слайд 19Преобразование Хафа (Hough)
Преобразование Хафа позволяет находить на бинарном изображении плоские
кривые, заданные параметрически, например: прямые, окружности, эллипсы, и т.д. Бинарное изображение
– изображение, пиксели которого принимают всего два значения (0 и 1). Считаем 0 – точками фона, 1 – «точками интереса». Задача преобразования Хафа состоит в выделении кривых, образованных точками интереса.Слайд 20Основная идея метода
Рассмотрим семейство кривых на плоскости, заданное параметрическим уравнением:
F(a1,
a2, …, an, x, y) = 0;
где F - некоторая
функция, a1, a2, ..., an - параметры семейства кривых, x, y - координаты на плоскости. Параметры семейства кривых образуют фазовое пространство, каждая точка которого (конкретные значения параметров a1, a2, ..., an) соответствует некоторой кривой.Идея преобразования Хафа состоит в поиске кривых (точек фазового пространства), которые проходят через достаточное количество точек интереса.
Слайд 21Машинное представление
Ввиду дискретности машинного представления и входных данных (изображения), требуется
перевести непрерывное фазовое пространство в дискретное.
Вводим сетку на фазовом пространстве
Каждой
ячейке сетки ставим в соответствие счетчикЗначение счетчика каждой ячейки устанавливаем равным количеству точек интереса, через которые проходит хотя бы одна кривая, параметры которой принадлежат данной ячейке.
Анализ счетчиков ячеек позволяет найти на изображении кривые, на которых лежит наибольшее количество точек интереса.
Слайд 22Выделение прямых на изображении
Прямую на плоскости можно задать следующим образом:
у = kx +b
x
cosθ + y sinθ = R,
R - длина перпендикуляра опущенного на прямую из начала координат,
θ - угол между перпендикуляром к прямой и осью OX,
θ изменяется в пределах от 0 до 2π , R ограничено размерами входного изображения.
Слайд 23Выделение прямых на изображении
Таким образом функция, задающая семейство прямых,
имеет
вид: F (R, θ, x, y) = x cosθ +
y sinθ - R.Через каждую точку (x, y) изображения можно провести несколько прямых с разными R и θ, то есть каждой точке (x, y) изображения соответствует набор точек в фазовом пространстве (R, θ). В свою очередь каждой точке пространства (R, θ) соответствует набор точек (x, y) на изображении, образующий прямую.
Слайд 24Изображение и фазовое пространство
Через одну точку можно провести несколько прямых.
Учитывая дискретность и введенную сетку, их будет конечное число.
Каждой прямой
пространства (x, y) соответствует точка фазового пространства (R, q). Прямые с левого рисунка образуют синусоиду.Слайд 25Изображение и фазовое пространство
Изображение с пятью точками интереса.
Кривые в фазовом
пространстве, соответствующие множеству прямых проходящих через каждую из точек.
Точки
пересечения кривых в фазовом пространстве соответствуют параметрам прямых, проходящих более чем через одну точку интереса.Слайд 26Дискретизация фазового пространства
Переводим непрерывное фазовое пространство в дискретное. Введем сетку
на пространстве (R, θ), одной ячейке которой соответствует набор прямых
с близкими значениями R и θ.Счетчик ставится в соответствие каждой ячейке сетки [Ri, Ri+1]x[θi,θi+1], равный числу точек интереса на изображении, удовлетворяющих уравнению:
x cosθ + y sinθ = R, где θi ≤ θ ≤ θi+1, Ri ≤ R ≤ Ri+1.
Слайд 27Алгоритм выделения прямых
обнулить счетчики всех ячеек;
для каждой точки интереса на
изображении:
для каждой прямой, проходящей через данную точку увеличить соответствующий счетчик;
выбрать
ячейки со значением счетчика, превышающим заданный порог;В общем случае алгоритм поиска прямой на изображении при помощи преобразования Хафа выглядит так:
Слайд 28Размер ячеек стоит выбирать аккуратно
Если ячейки будут очень большими, то
за «прямую» может приниматься разрозненный набор точек.
Если же наоборот,
ячейки будут слишком малы, есть вероятность, что ни одной прямой не найдется – все счетчики будут иметь небольшое значение.
Слайд 39
Обобщенное преобразование Хафа
Задача: Обнаружение фигуры заданной формы.
+
О
Этап 1. Обучение
(построение LUT)
Слайд 40
Обобщенное преобразование Хафа
Задача: Обнаружение фигуры заданной формы.
+
О
Этап 1. Обучение
(построение LUT)
Слайд 41
Обобщенное преобразование Хафа
Задача: Обнаружение фигуры заданной формы.
+
О
LUT
Этап 1. Обучение
(построение LUT)
Слайд 42
Обобщенное преобразование Хафа
Задача: Обнаружение фигуры заданной формы.
+
О
LUT
Голосующая точка
Этап 2.
Обнаружение (голосование точек и анализ аккумулятора)
Слайд 43
Обобщенное преобразование Хафа
Задача: Построение окружности по полутоновому образу.
гмт
O
Касательная в точке
Радиус-вектор
в точке
Градиент в точке
Слайд 44
Обобщенное преобразование Хафа
гмт
Касательная в точке
O
Градиент в точке
Задача: Построение окружности по
полутоновому образу.
Слайд 47Обобщенное преобразование Хафа
+
О
Касательная в точке
Градиент в точке
Радиус-вектор в точке
Угол
между градиентом
и радиус-вектором
R
ϕ
Задача: Инвариантное обнаружение по полутоновому образу.
Слайд 48Обобщенное преобразование Хафа
+
О
Касательная в точке
Градиент в точке
Радиус-вектор в точке
Угол
между градиентом
и радиус-вектором
ϕ
ϕ
ϕ
LUT: R(ϕ)
Задача: Инвариантное обнаружение по полутоновому образу.
Слайд 50Морфологии Серра на базе преобразования Хафа
Монотонная морфология на базе преобразования
Хафа и GHT
H-открытие - объединение проекций изображения A(p) на отдельные
прямые линии:
Pr(A(p),t) = MAXq∈Q(A(q,t)∙Pr(A(p),ϕ(p,q))) = MAXq∈Q(A(q,t)∙A(p)∙ϕ(p,q)),где p=(x,y); q=(ρ,θ) – параметры нормальной параметризации прямой; Q – пространство параметров; ϕ(p,q)∈{0,1} – характеристическая функция прямой с параметрами q; A(q,t)∈{0,1} – аккумулятор преобразования Хафа, бинаризованный по порогу t.
(а) (b) (с)
Пример морфологического H-открытия: a – исходное бинарное изображение; b – аккумулятор пространства Хафа c – результат H-открытия. На исходном контурном препарате выделены глобальные прямолинейные структуры.
Аналогичным образом строится монотонная проективная морфология на базе
обобщенного преобразования Хафа (GHT).