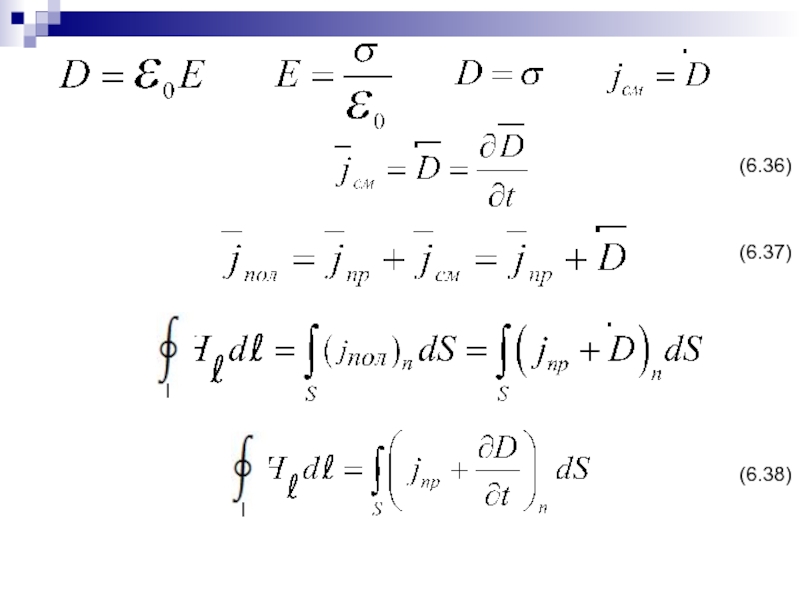Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по курсу Общая физика
Содержание
- 1. Презентация по курсу Общая физика
- 2. Оглавление.МеханикаМолекулярная физика и термодинамикаЭлектростатикаПостоянный токМагнетизмЭлектрические колебанияКвантовая физикаОптикаАтомная и ядерная физика
- 3. I.МЕХАНИКА В оглавление
- 4. 1.Кинематика1.1Скорость = элементарный путь.- элементарное перемещение.Скорость – производная радиуса векторадвижущийся точки по времени:yx0Рис. 1.112
- 5. При малых ∆t
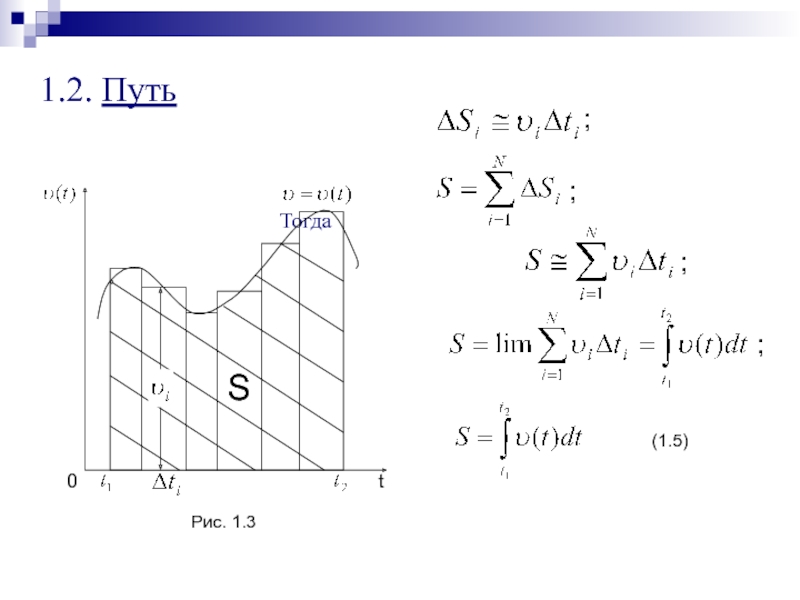
- 6. 1.2. Путь Тогда S0tРис. 1.3 (1.5);;;;
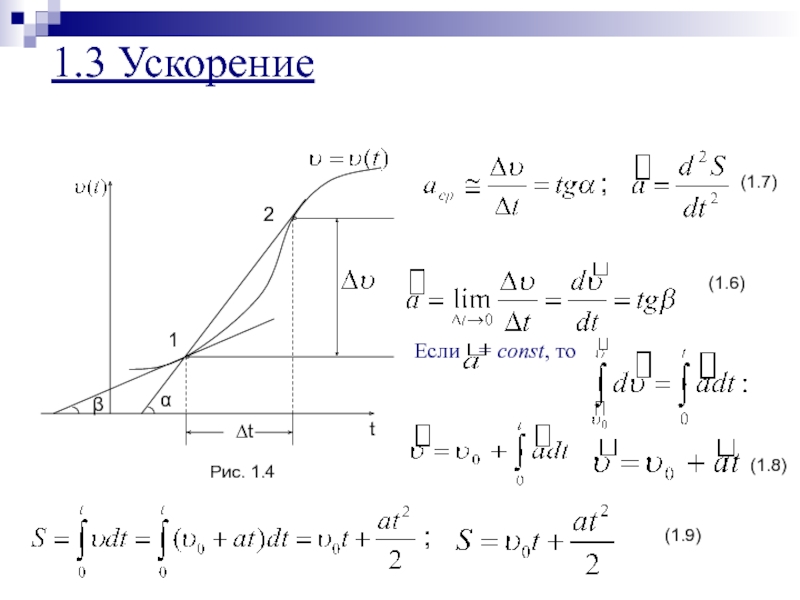
- 7. 1.3 Ускорение
- 8. 1.4. Ускорение при криволинейном движении
- 9. 1.5. Кинематика вращательного движения
- 10. 2. Динамика материальной точки 2.1 Первый
- 11. 2.2 Второй закон Ньютона2.3Третий закон Ньютона
- 12. 2.4 Закон сохранения импульса2.5 Принцип относительности Галилея
- 13. 3. Работа и энергия.3.1.Работа.SAРабота на каждом элементарном участкеНа всем путиРис. 1.9 (1.26)Интегральная формула работы
- 14. 3.2. Мощность.Мощность - работа механизма за единицу
- 15. 3.5. Потенциальная энергия.
- 16. 4. Центральный удар шаров.4.1. Абсолютно упругий удар
- 17. б) Абсолютно неупругий удар.Затем (1.41) +
- 18. 5. Динамика вращательного движения. 5.1. Момент силы
- 19. 5.2. Момент силы относительно оси.5.3. Момент инерции. Физическая
- 20. Момент инерции J относительно произвольной оси равен
- 21. а) Для цилиндра и диска относительно совпадения
- 22. в) Для шара относительно оси, проходящей через
- 23. 5.6. Основной закон динамики вращательного движения.Для всего абсолютно твердого телаРис. 1.19(1.55)
- 24. а) Для материальной точки. б) Для твердого тела. в)
- 25. 5.8. Кинетическая энергия вращения твердого тела.Рис. 1.20(1.61);
- 26. 5.9. Работа внешних сил при вращении твердого тела.,но Рис 1.20(а);;;
- 27. 5.10. Кинетическая энергия тела при плоских движениях.Кинетическая энергия i-ой элем. массы равна(1.62);
- 28. 6. Колебательное движение6.1 Гармонические колебания.Колебания, происходящие по
- 29. Рассмотрим математический маятник (рис.1.21(б))lmgРис. 1.21(б) , тогда В то же время,
- 30. Число колебаний в единицу времени называется частотой
- 31. Из начальных условий (t=0)(1.68)(1.69)
- 32. 6.2. Энергия гармонического колебания.(1.70)(1.71)(1.72)
- 33. 6.3 Сложение колебаний одинакового направления. Колебания изображаются графически в виде векторов на плоскости.(1.73)(1.74)(1.75)
- 34. 6.4. Сложение взаимноперпендикулярных колебаний. Частоты определяются первого колебания: а) одинаковая частота 1) 2) 3)Рис. 1.24(1.76)второго колебания:
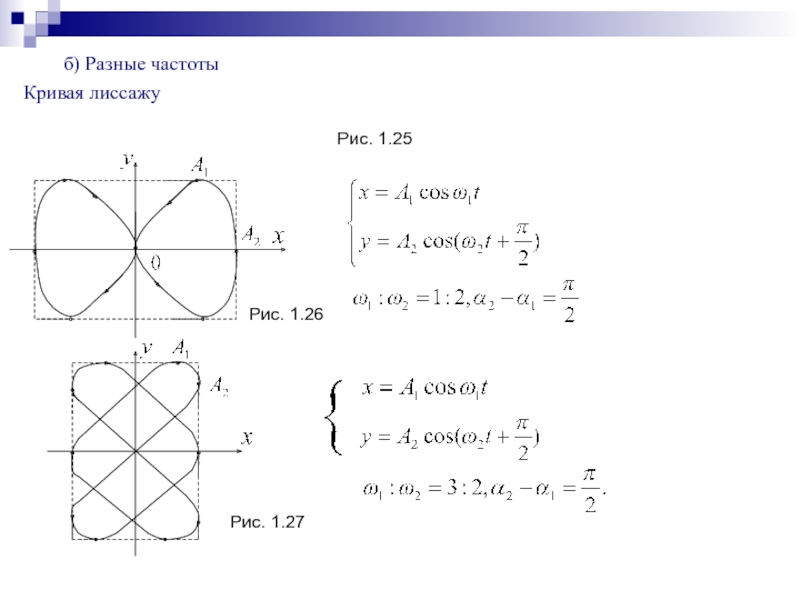
- 35. б) Разные частотыКривая лиссажу
- 36. 6.5. Затухающие колебанияиРешение уравнения (1) будем искать
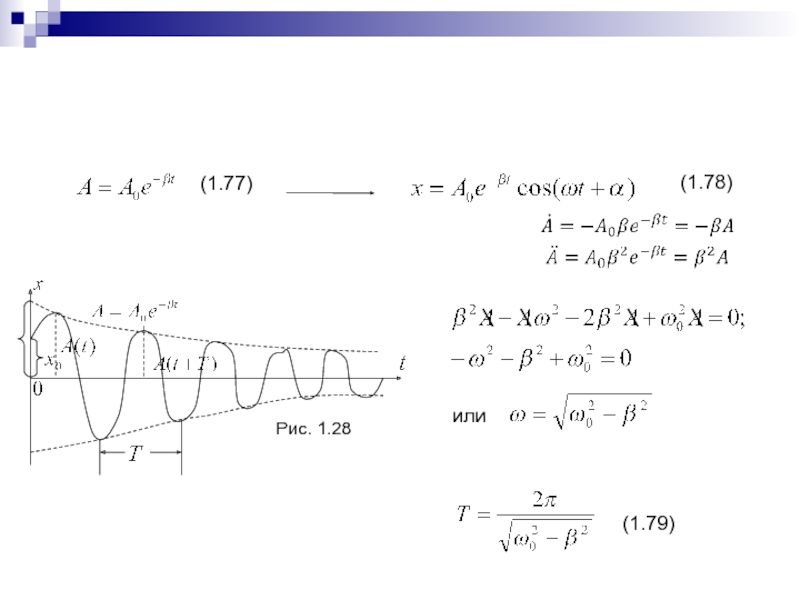
- 37. Рис. 1.28(1.77)(1.78)(1.79) \\\\или
- 38. Слайд 38
- 39. 6.6. Вынужденные колебания.
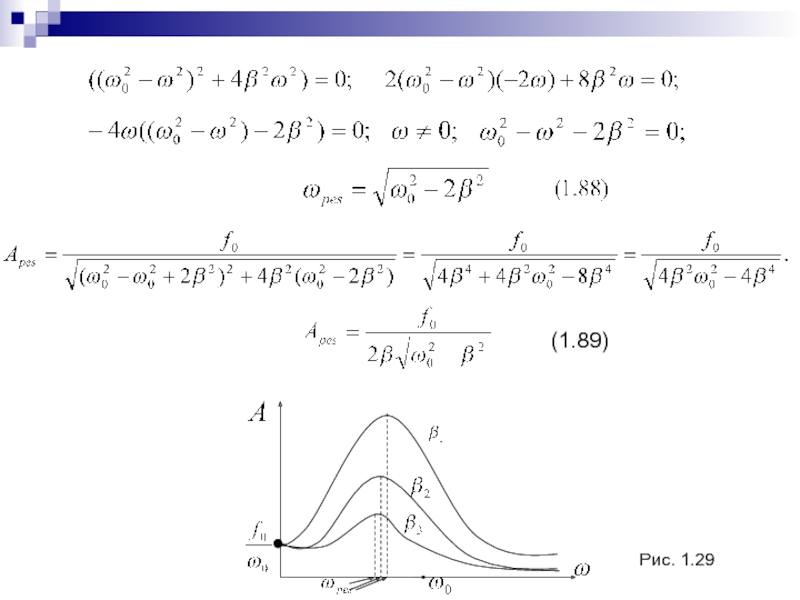
- 40. Рис. 1.29(1.89)
- 41. 7. Волны.7.1. Уравнение плоской и сферической волн. Уравнением
- 42. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКАВ оглавление
- 43. 1.1 Состояние системы. Процесс.Рис. 2.12. МОЛЕКУЛЯРНАЯ ФИЗИКА.
- 44. 1.3 Температура.1.4 Уравнение состояния идеального газа. (2.3)(2.2)(2.1)Соотношение,
- 45. Закон Гей-Люссака.Закон Бойля-Мариотта.Закон Шарля. (V=const). Изохорный процесс.(2.4)(2.6)(2.5)(P=const). Изобарный процесс. P1V1=P2V2 (T=const). Изотермический процесс
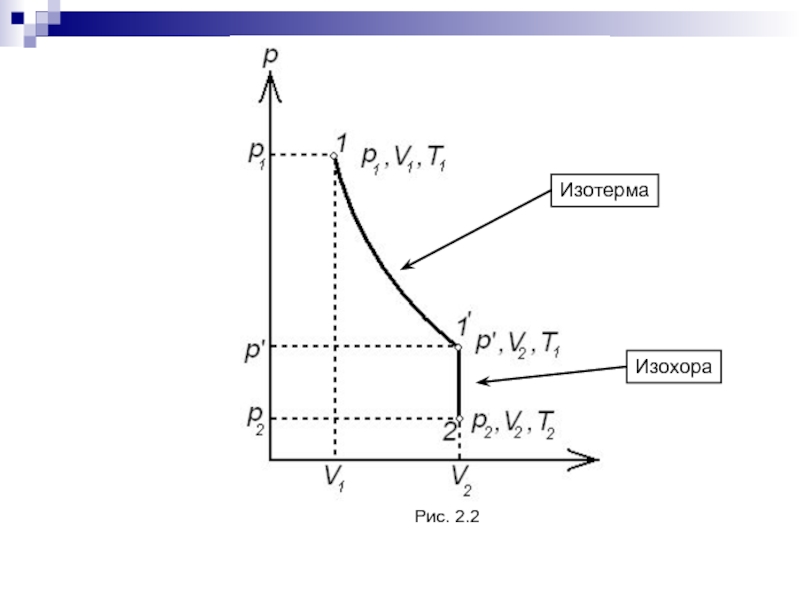
- 46. Рис. 2.2ИзотермаИзохора
- 47. где В – постоянная для данной массы газа величина.(2.7)(2.8)(2.9)(2.10)- Уравнение Клайперона- уравнение Менделеева-Клайперона
- 48. 1.5 Уравнение кинетической теории газов для давления.(2.11)(2.12)(2.13)(2.14)- постоянная Больцмана
- 49. 1.6 Распределение молекул газа по скоростям. Функция
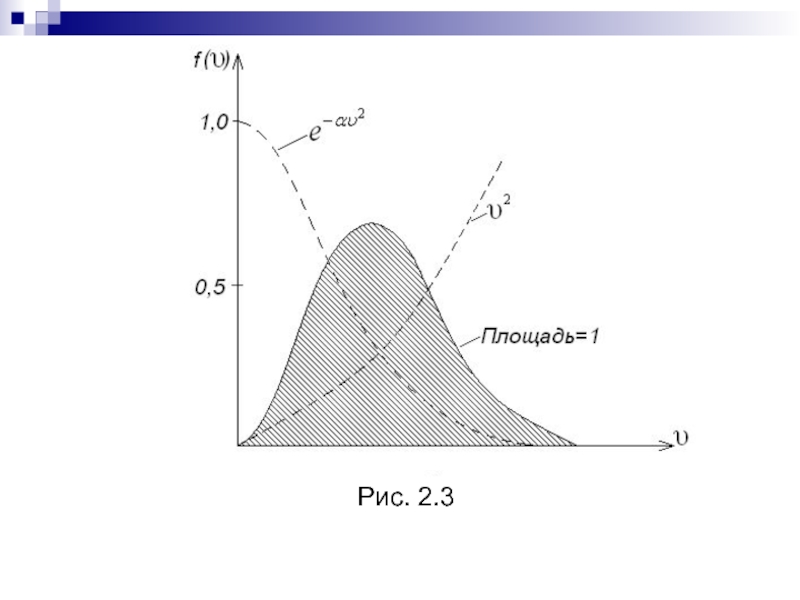
- 50. Рис. 2.3
- 51. 2. ОСНОВЫ ТЕРМОДИНАМИКИ(2.16)(2.18)(2.17)Уравнение (2.18) выражает закон сохранения
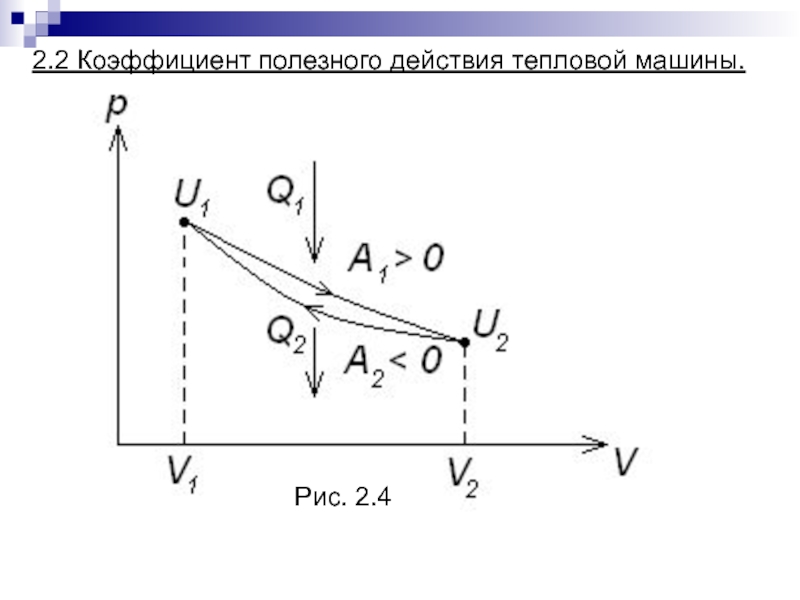
- 52. 2.2 Коэффициент полезного действия тепловой машины.Рис. 2.4
- 53. (2.19)(2.20)(2.21)(2.22)(2.23)Складывая уравнения (2.19) и (2.20), получаем:Тепловую машину
- 54. 2.3 Второе начало термодинамики.Второе начало термодинамики, как
- 55. III.ЭЛЕКТРОСТАТИКА В оглавление
- 56. 1. Электрическое поле в вакууме. 1.2 Взаимодействие зарядов. Закон Кулона. Рис. 3.11.1 Введение.
- 57. (3.3(а))(3.2)(3.3(б));;1.3 Электрическое поле. Напряженность поля. Рис. 3.2(3.1);;
- 58. 1.4 Линии напряженности. Поток вектора напряженности. ;
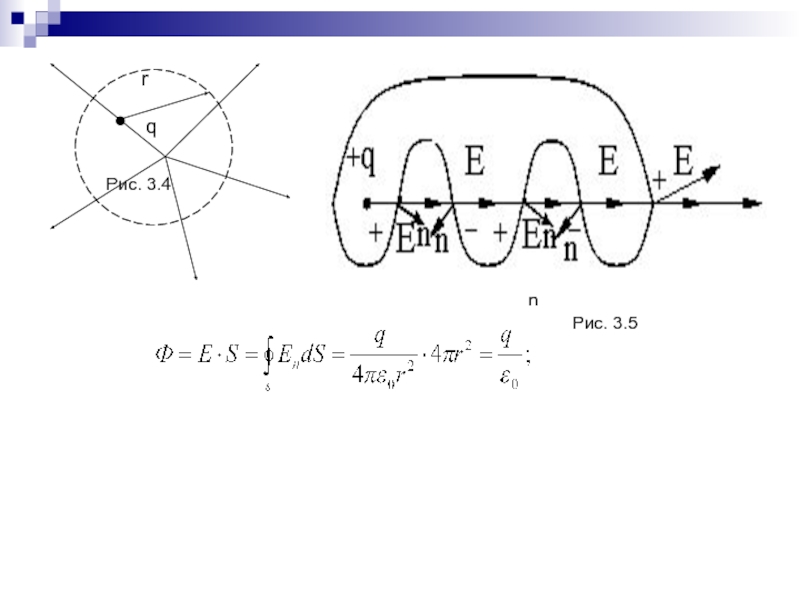
- 59. Рис. 3.4Рис. 3.5rqn
- 60. 1.5 Теорема Гаусса. (3.7), где(3.8)(3.9)
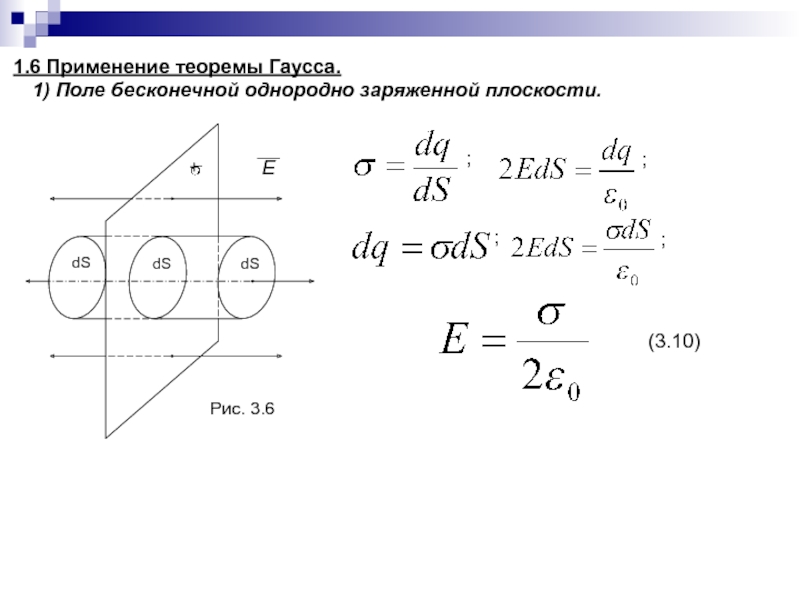
- 61. 1.6 Применение теоремы Гаусса.1) Поле бесконечной однородно заряженной плоскости.Рис. 3.6(3.10);;;;
- 62. 2) Поле двух равномерно и разноименно заряженных
- 63. 4) Поле заряженной сферической поверхности.5) Поле объемно
- 64. 1.7 Работа сил электрического поля. Рис. 3.13Рис. 3.14(3.16)(3.17)ε0ε0ε0ε0;.;;;.
- 65. B СИ и U измеряется в Вольтах:(3.19)(3.21)(3.20)ε0ε0ε0;;1.8 Потенциал. Разность потенциалов. (3.18)ε0.
- 66. Рис. 3.15Рис. 3.16(3.22)(3.23)(3.24);;1.9 Связь между E и .
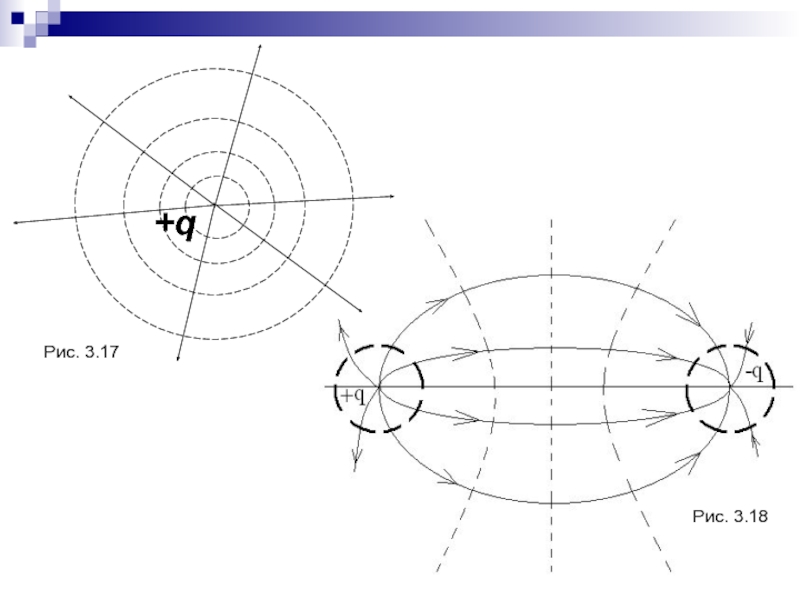
- 67. Рис. 3.17Рис. 3.18
- 68. 2. Электрическое поле в диэлектриках. 2.1 Полярные и неполярные молекулы. Рис. 3.20Рис. 3.21Рис. 3.19(3.26)(3.25)ε0+q-q
- 69. 2.2 Поляризация диэлектриков. Деформационная поляризацияОриентационная поляризацияРис. 3.23Рис. 3.22(3.28)(3.27)
- 70. 2.3 Поле в диэлектриках. Рис. 3.24(3.32)(3.31)(3.30)(3.29)(3.33)
- 71. 2.4 Проводники в электрическом поле. Рис. 3.25(3.34)ε0ε2) На поверхности
- 72. 2.5 Проводники во внешнем электрическом поле. 2.6
- 73. 2.7 Конденсаторы. 1) Плоский конденсатор.Рис. 3.27(3.38)(3.37);;
- 74. 2) Цилиндрический конденсатор. Рис. 3.28(3.39)1;
- 75. 3) Сферический конденсатор.Рис. 3.29(3.40)(3.41)
- 76. 2.8 Соединение конденсаторов. Рис. 3.30(3.41)2)Параллельное соединение.3) Смешанное соединение.Рис. 3.31Рис. 3.32(3.42)1) Последовательное соединение.
- 77. 2.9 Энергия электрического поля. Рис. 3.33(3.43);;;;;;;1) Энергия системы зарядов.
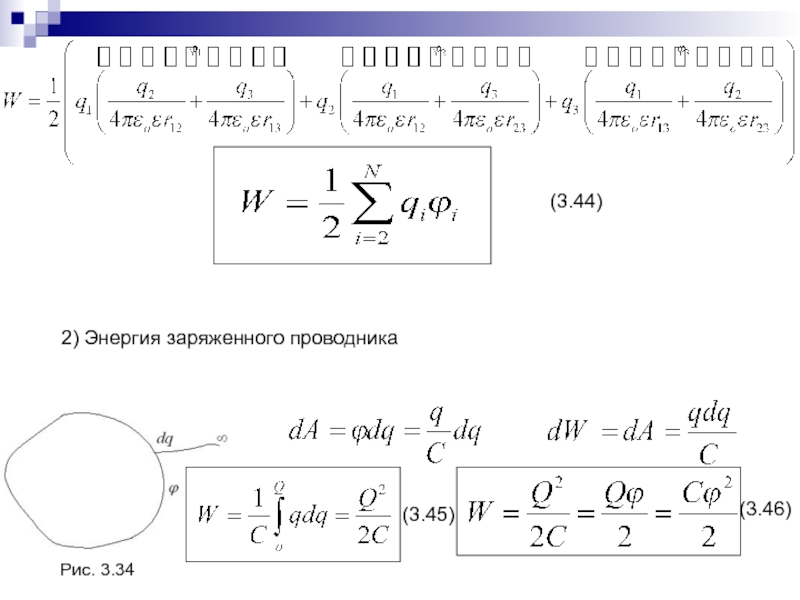
- 78. (3.44)Рис. 3.34(3.45)(3.46)2) Энергия заряженного проводника
- 79. 3) Энергия заряженного конденсатора.Рис. 3.35(3.47)
- 80. 4) Энергия электрического поля.Плотность энергииРис. 3.36(3.48)(3.49)(3.50)S;;;
- 81. IV.ПОСТОЯННЫЙ ТОКВ оглавление
- 82. 4.1. Сила тока Сила тока I есть
- 83. Отсюдатогда Из рис 4.1 видно, что
- 84. 4.3. Закон Ома для однородного участка
- 85. где - сопротивление этого участка. Подставляя в
- 86. 4.5. Электродвижущая сила. Закон Ома для замкнутой
- 87. тогда имеемилиЗакон Ома для замкнутой цепи., получим
- 88. 4.6. Закон Ома для неоднородного участка цепи
- 89. Складывая последние равенства, найдем:Здесьгде ε - ЭДС,
- 90. Этот закон является наиболее общим законом Ома,
- 91. 4.7. Мощность, выделяемая в цепи. Но так
- 92. Мощность, выделенная на внешнем участке цепи, Pa
- 93. 4.8. Закон Джоуля-Ленца. Интегральная форма закона. Если I изменяется со временем, то(4.39)(4.38)(4.37)(4.36)
- 94. 4.9. Закон Джоуля-Ленца в дифференциальной форме. Плотность
- 95. 4.10. Классическая электронная теория металлов Рис. 4.6
- 96. 4.11. Закон Ома с точки зрения классической
- 97. Где m - масса электрона.(4.49) По второму
- 98. Закон Джоуля-Ленца с точки зрения классической теорииПодсчитаем
- 99. Плотность тепловой мощности:где , окончательно имеем: что является законом Джоуля-Ленца.,(4.58)(4.59)
- 100. V. МАГНЕТИЗМ В оглавление
- 101. 1. Магнитное поле в вакууме. 1.1. Магнитное поле и его характеристика. Рис. 5.1а)б)в)
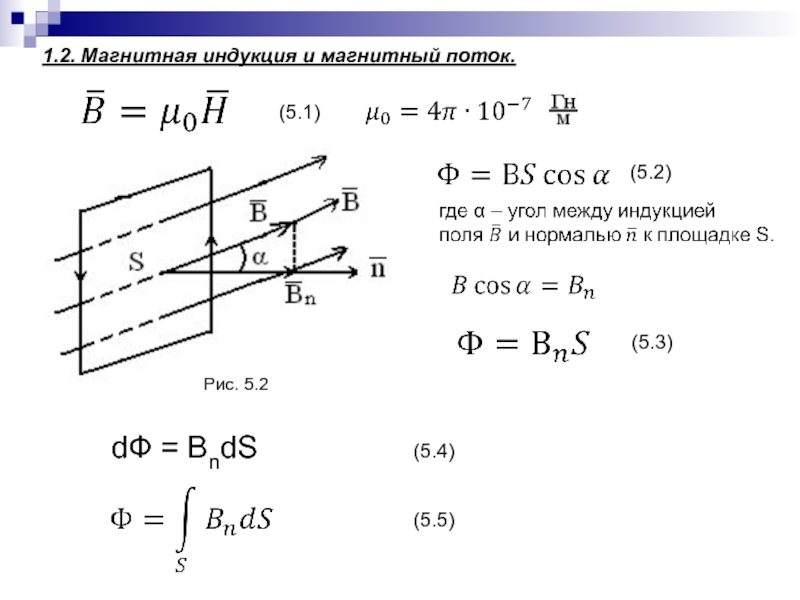
- 102. 1.2. Магнитная индукция и магнитный поток. (5.1)(5.3)Рис.
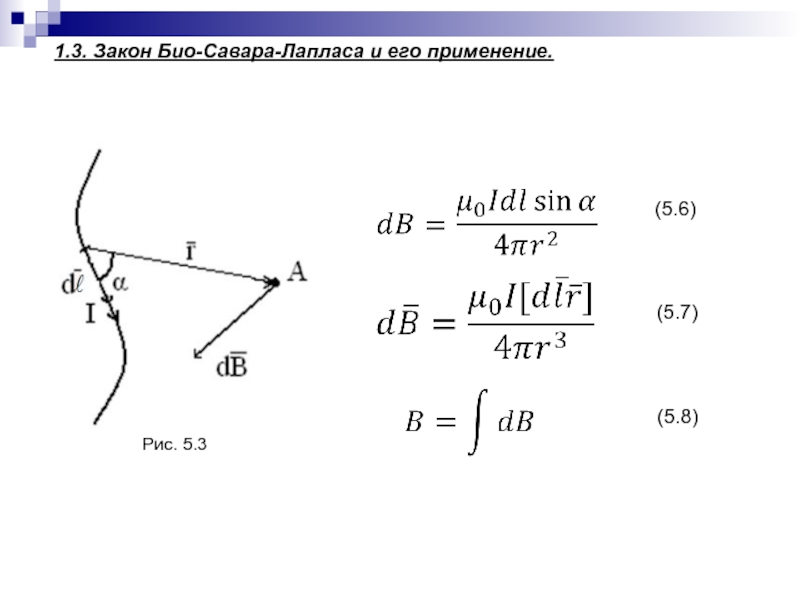
- 103. 1.3. Закон Био-Савара-Лапласа и его применение.
- 104. Применение закона Био-Савара-Лапласа.Пример I. Магнитное поле прямого провода с током.(5.9)(5.10)(5.11)(5.12)
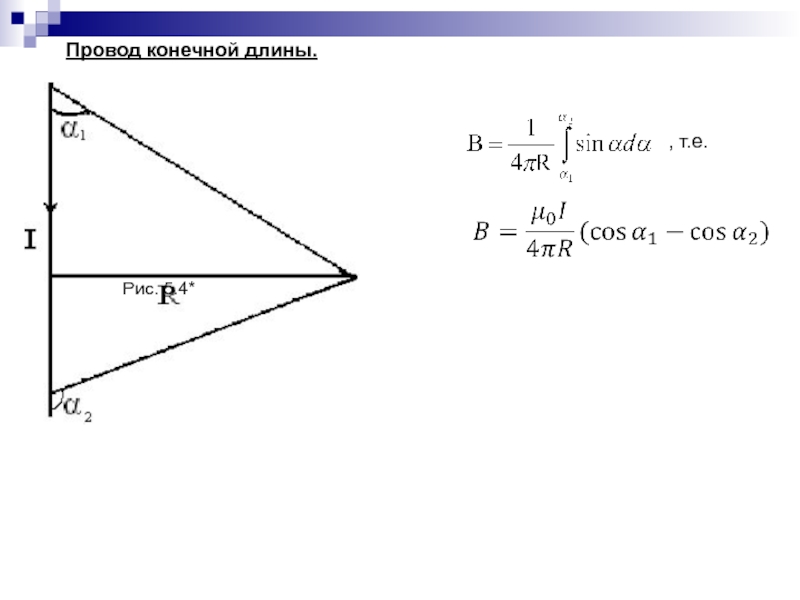
- 105. Провод конечной длины., т.е.Рис. 5.4*
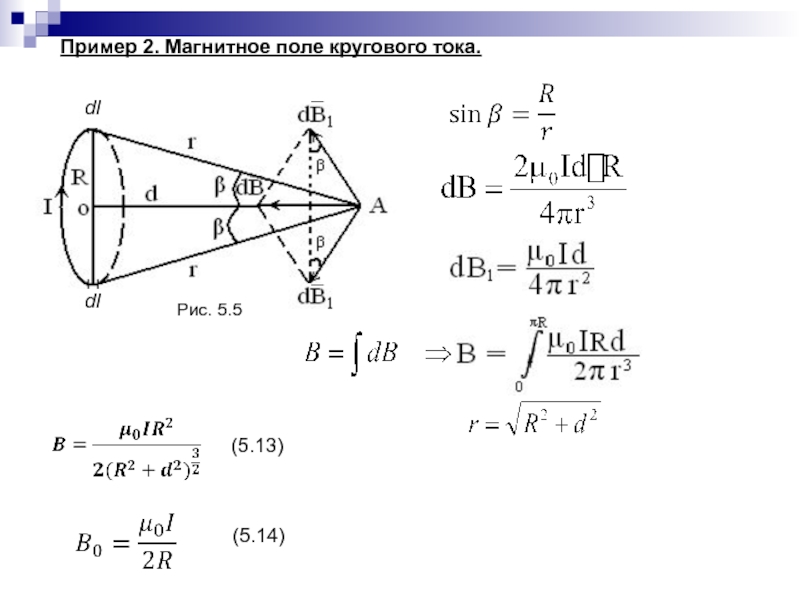
- 106. Пример 2. Магнитное поле кругового тока.(5.13)(5.14)Рис. 5.5dldl
- 107. Пример 3. Магнитное поле на оси соленоида.(5.15)Для
- 108. 1.4. Циркуляция вектора магнитной индукции.(5.17)(5.18)и dlcosα =
- 109. 1.5. Закон Ампера.
- 110. 1.6. Вращающий и магнитный момент для контура
- 111. 1.7. Магнитное взаимодействие токов. (5.27)(5.28)(5.29)Рис. 5.10
- 112. 1.8. Работа перемещения контура с током в
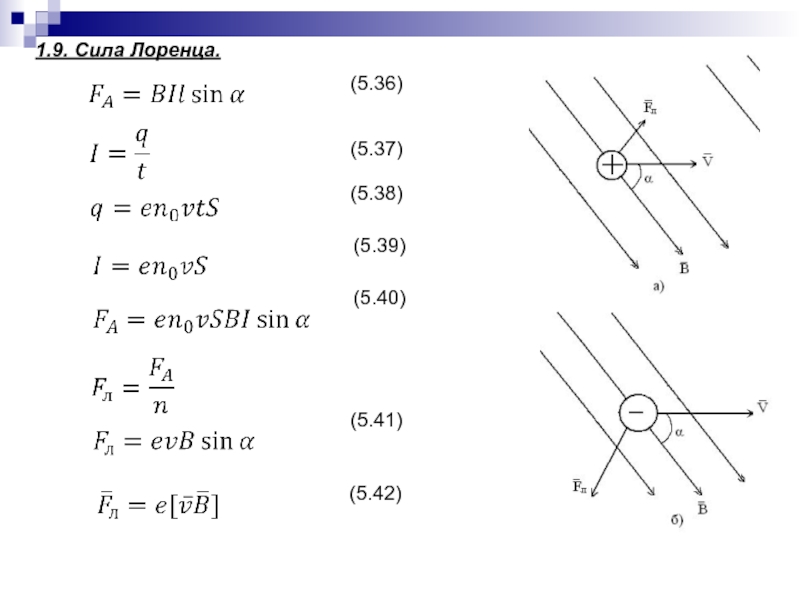
- 113. 1.9. Сила Лоренца.(5.36)
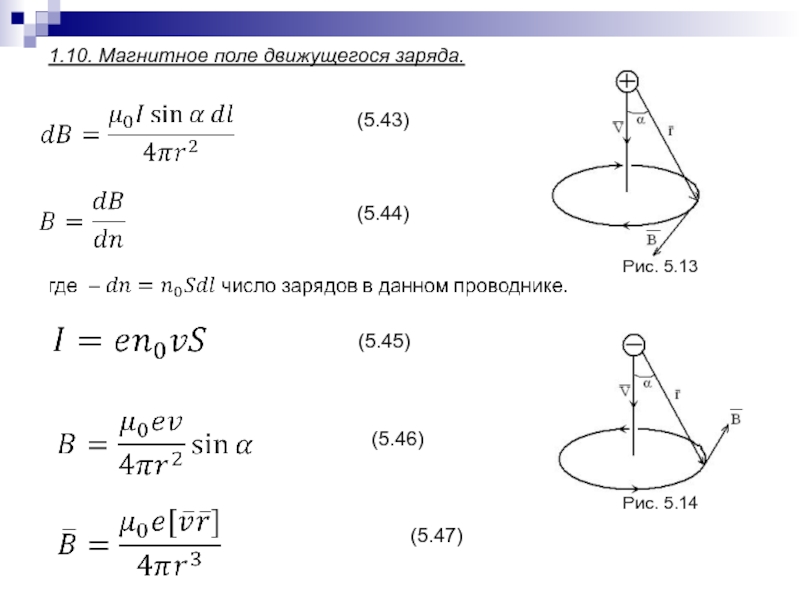
- 114. 1.10. Магнитное поле движущегося заряда. (5.43)(5.44)(5.45) (5.46)Рис. 5.13Рис. 5.14(5.47)
- 115. 2.Магнитное поле в магнетиках. 2.1. Намагничивание веществ.
- 116. 2.2. Магнитное поле в магнетике. Вектор магнитной
- 117. 2.3. Диамагнетизм и парамагнетизм.
- 118. Для ферромагнетиков >>1 и >>0. Характерной особенностью
- 119. Зависимость между вектором намагничивания Р и Н
- 120. На рисунке показан график
- 121. 3. Электромагнитная
- 122. 3.2. Э. Д. С. индукции. Закон Фарадея. (5.59)Рис. 5.23
- 123. 3.3. Электронный механизм возникновения ЭДС индукции.
- 124. Рис. 5.25(5.60)3.4.ЭДС индукции возникающая в движущимся проводнике в магнитном поле.(по правилу левой руки)
- 125. 3.5. Заряд, перемещенный индукционным током. (5.61) (5.62) (5.63)(5.64)(5.65)
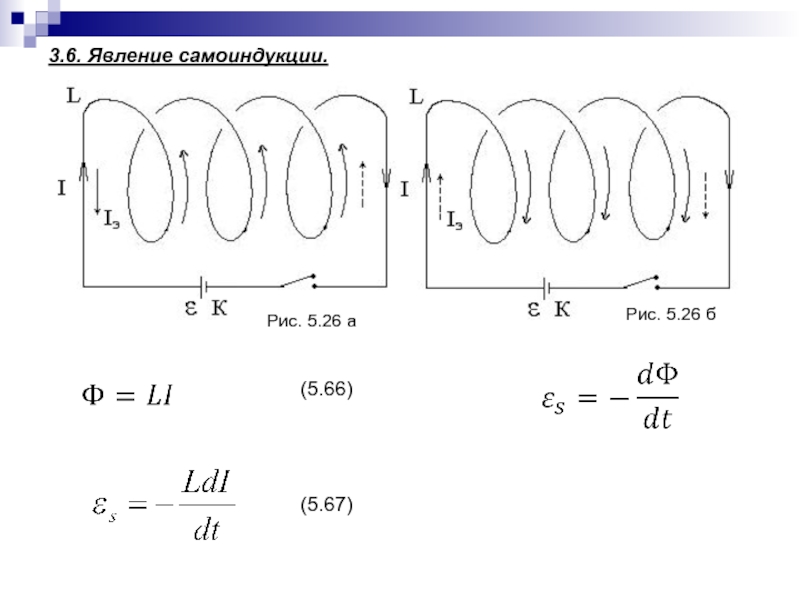
- 126. 3.6. Явление самоиндукции. (5.66)(5.67)Рис. 5.26 аРис. 5.26 б
- 127. 3.7. Индуктивность соленоида. Где n – число
- 128. 3.8. Взаимная индукция. (5.71)Здесь L21 – коэффициент
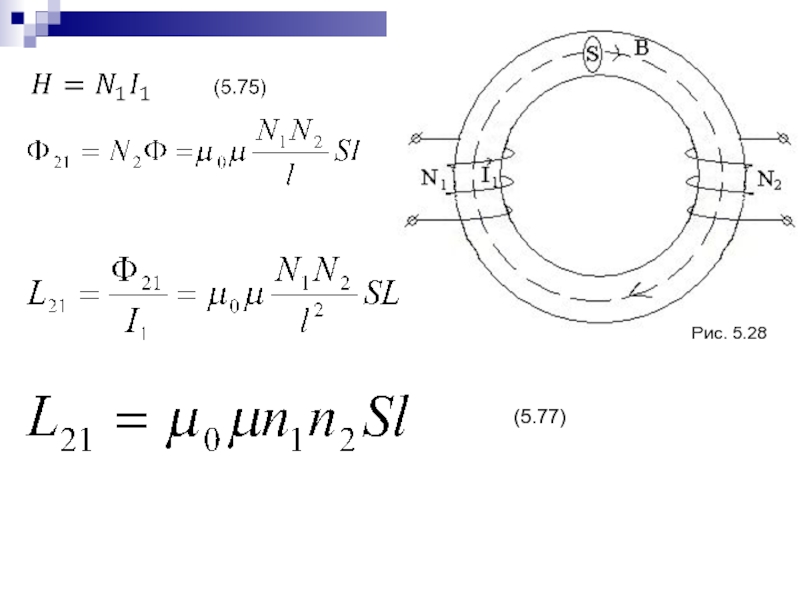
- 129. Рис. 5.28(5.77)
- 130. 3.9. Энергия магнитного поля. (5.78)(5.79)
- 131. Подставляя (5.80) в (5.78), имеем или после
- 132. Слайд 132
- 133. Слайд 133
- 134. Слайд 134
- 135. Слайд 135
- 136. VI.ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ В оглавление
- 137. 1.1 Свободные колебания в контуре без активного сопротивления (R=0)(6.1) Рис. 6.11. Электрические колебания
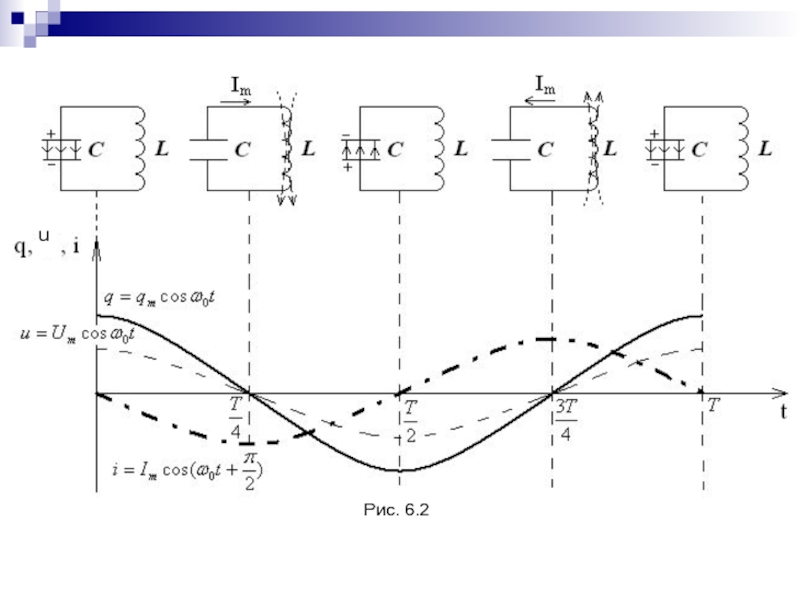
- 138. Рис. 6.2u
- 139. Для колебательного контура по 2-му правилу Кирхгофа:
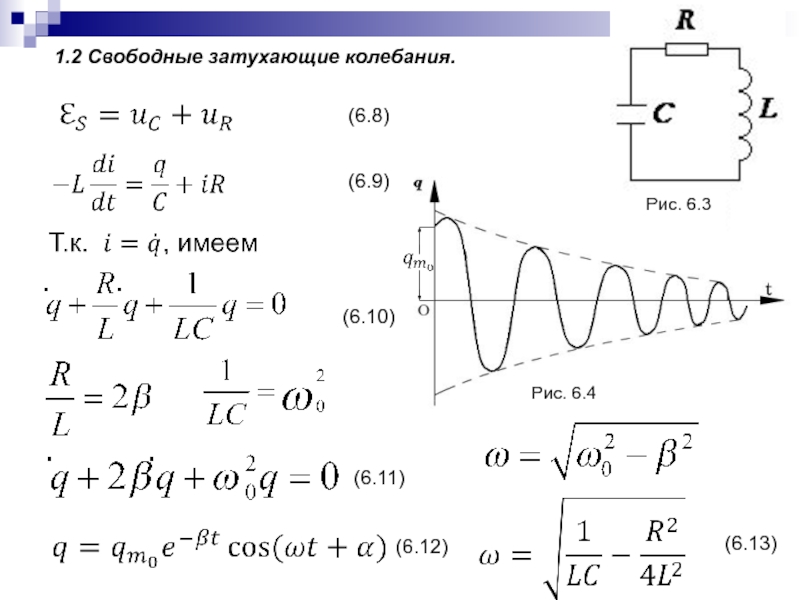
- 140. 1.2 Свободные затухающие колебания. (6.8) (6.9) (6.10) (6.11) (6.12) Рис. 6.3(6.13)
- 141. (6.14) (6.15) (6.16) где A(t)-амплитуда соответствующей величины q, u или i.
- 142. (6.18) (6.19) (6.20) 3.1 Вынужденные электрические колебания.(6.17)
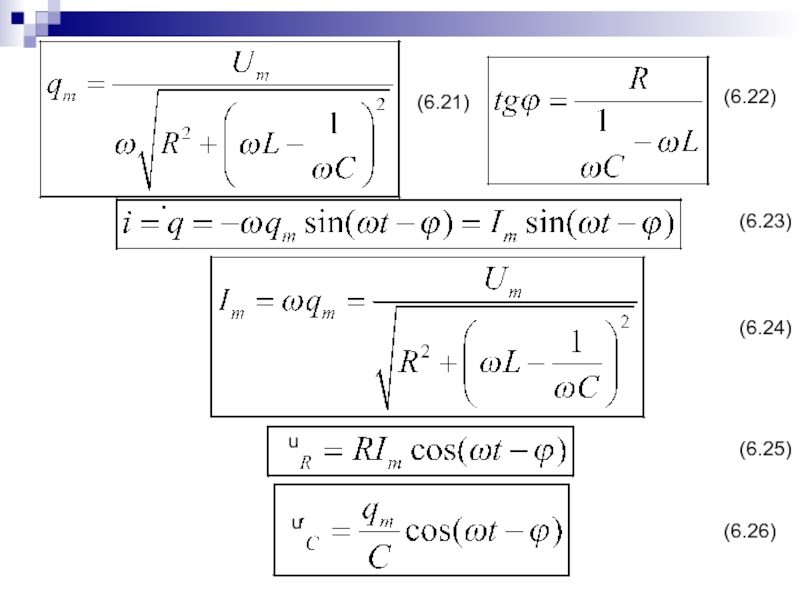
- 143. (6.21) (6.22) (6.23) (6.24) (6.25) (6.26) uu
- 144. (6.27) (6.28) 2. Электромагнитное поле.2.1 Вихревое электрическое поле.(6.29) (6.30) ulll
- 145. (6.31), где и (6.32) (6.33) 2.2 Ток смещения. (6.34) (6.35) Рис. 6.6l
- 146. (6.36) (6.37) (6.38) ll
- 147. § 3. Электромагнитное поле. Уравнение Максвелла.(6.39) (6.40) (6.41) (6.42) llsj
- 148. 3. Электромагнитные волны.3.1. Плоская электромагнитная волна.(6.43) (6.45) (6.44) Рис. 6.7
- 149. 3.2. Энергия электромагнитного поля.(6.46)(6.47)(6.48)- вектор Умова-Пойнтинга.
- 150. VII.КВАНТОВАЯ ФИЗИКАВ оглавление
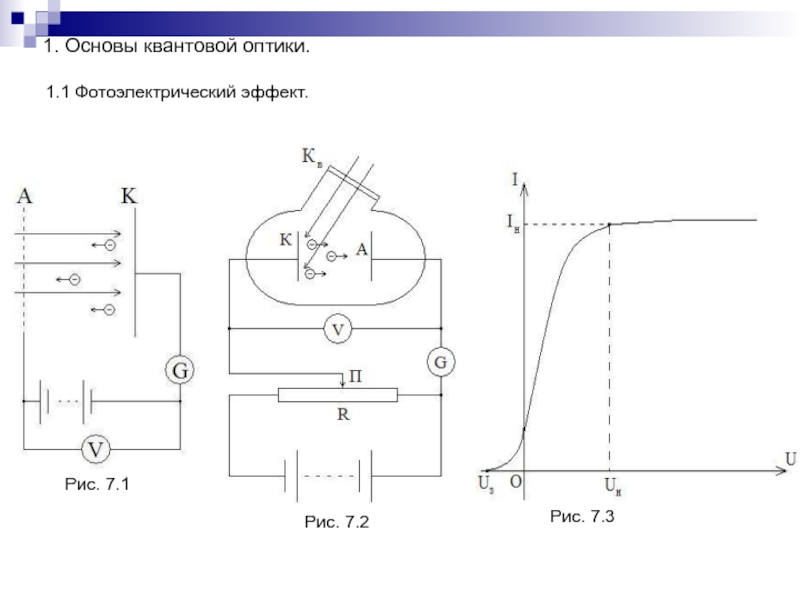
- 151. 1. Основы квантовой оптики.1.1 Фотоэлектрический эффект.Рис. 7.1Рис. 7.2Рис. 7.3
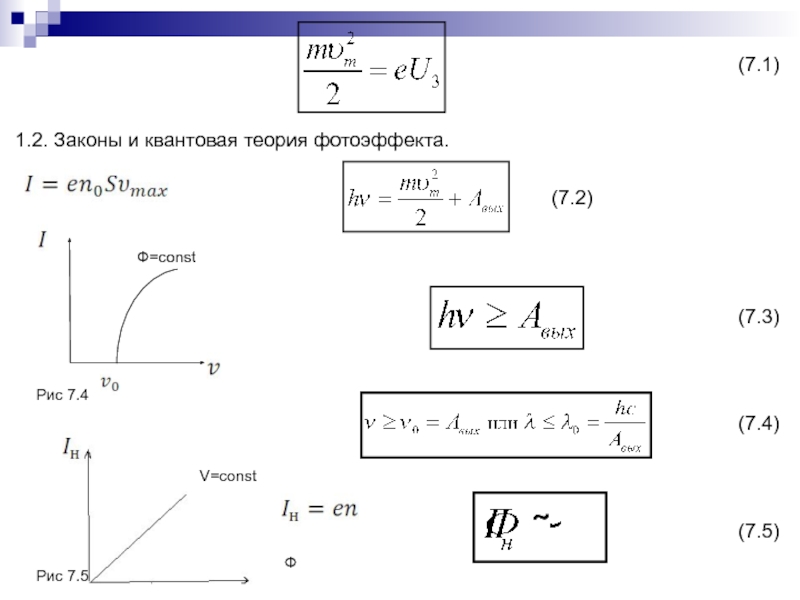
- 152. 1.2. Законы и квантовая теория фотоэффекта.(7.1)(7.2)(7.3)(7.4)(7.5)˜Ф=constРис 7.4V=constФРис 7.5
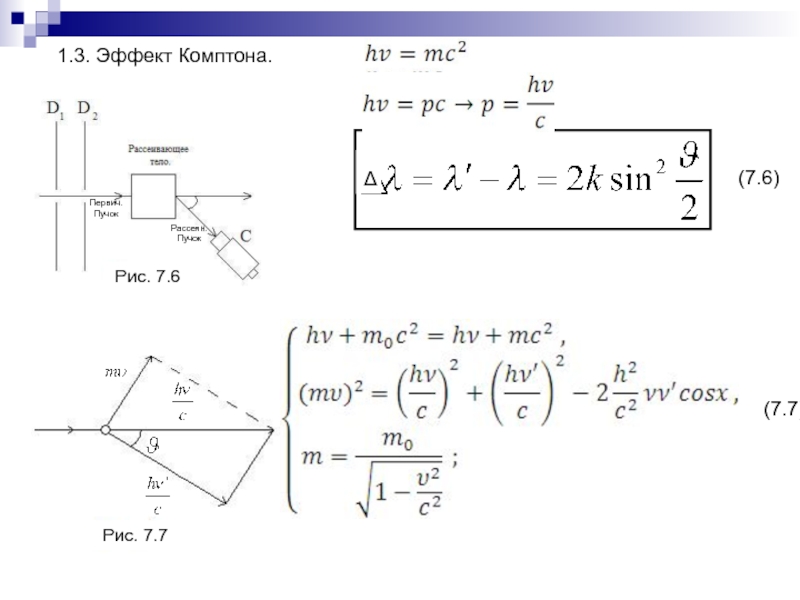
- 153. 1.3. Эффект Комптона.Рис. 7.6Рис. 7.7(7.7)(7.6)ΔПервич.ПучокРассеян.Пучок
- 154. Докажем, что
- 155. Вернемся к уравнению (3):Подставим в систему преобразованные уравнения (4) и (5):Вычитаем
- 156. С помощью тригонометрических уравнений:Подставляем: Вернемся к начальной системеПодставим в выражение:
- 157. Используем формулуОбозначим
- 158. 2. Элементы квантовой механики.2.1. Корпускулярно-волновая двойственность свойств частиц вещества. 2.2. Соотношения неопределенностей Гейзенберга.(7.11)(7.9)(7.10)(7.12)(7.13)(7.14)(7.15)ΔΔΔΔΔ
- 159. 3. Зонная теория твердых тел.3.1. Энергетические уровни электронов.Рис. 7.8Рис. 7.8*Рис. 7.9(7.17)(7.16)(7.18)
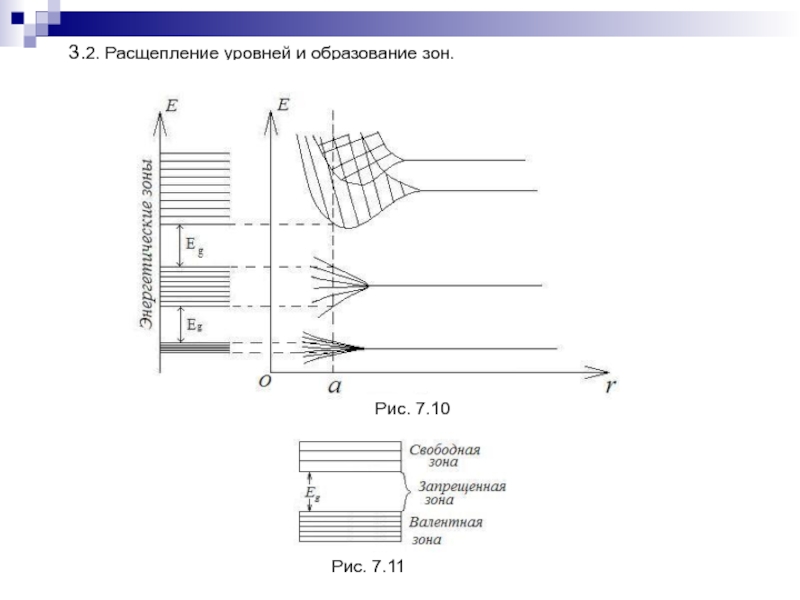
- 160. 3.2. Расщепление уровней и образование зон.Рис. 7.10Рис. 7.11
- 161. 3.3. Заполнение энергетических зон электронами.Рис. 11Рис. 7.12(7.19)При
- 162. 3.4. Проводники, диэлектрики и полупроводники.Рис. 7.13
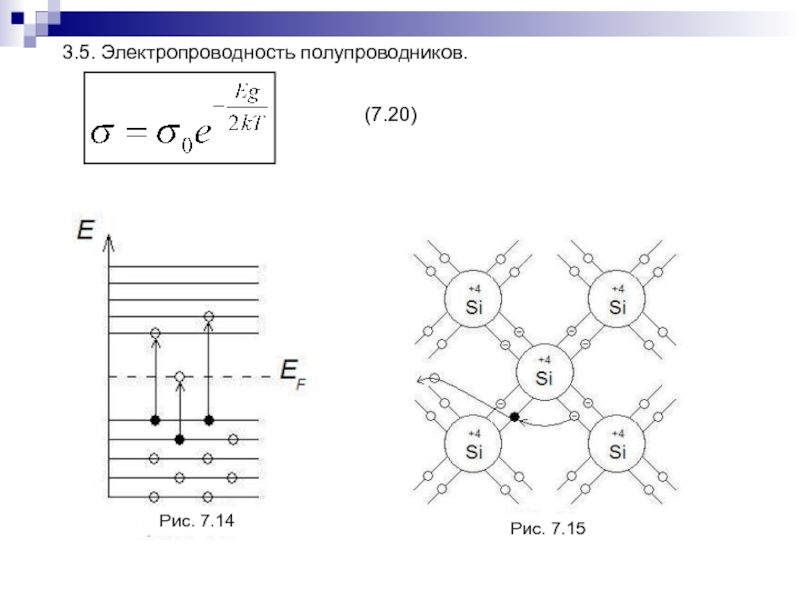
- 163. 3.5. Электропроводность полупроводников.Рис. 7.14Рис. 7.15(7.20)
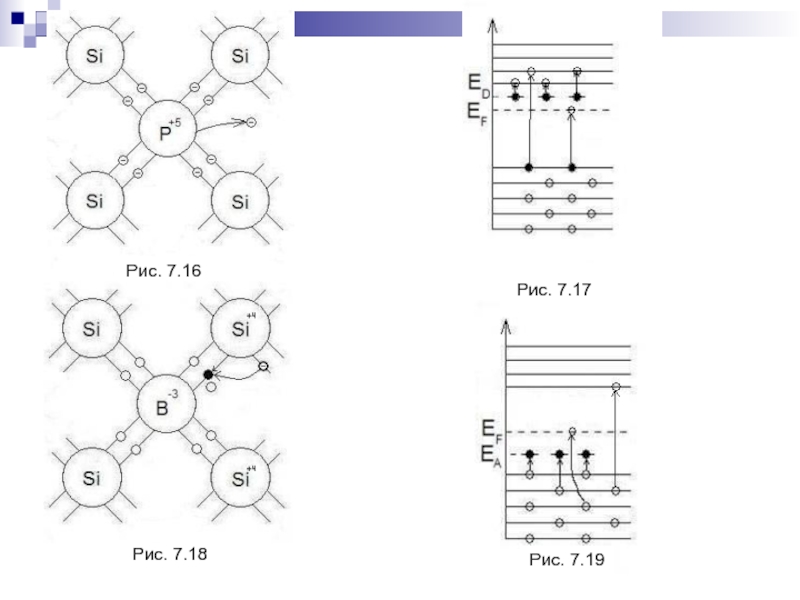
- 164. Рис. 7.17Рис. 7.16Рис. 7.18Рис. 7.19
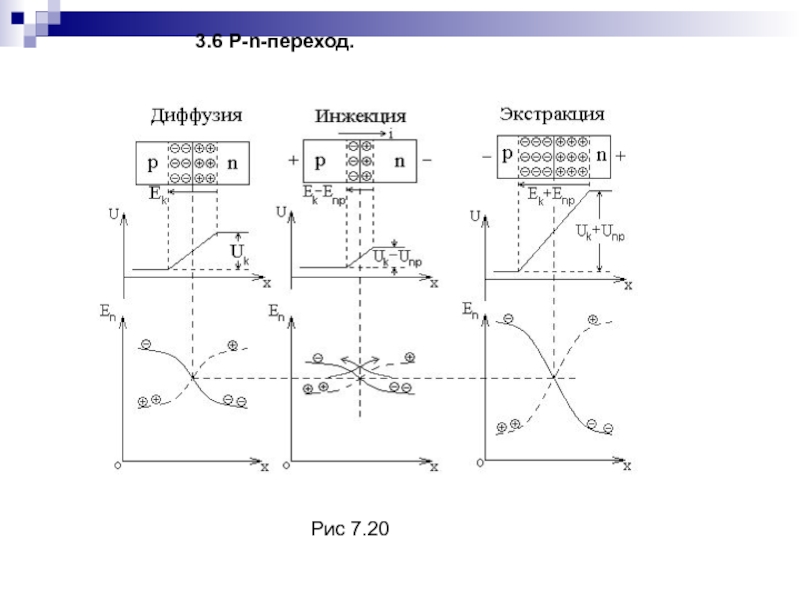
- 165. 3.6 P-n-переход.Рис 7.20
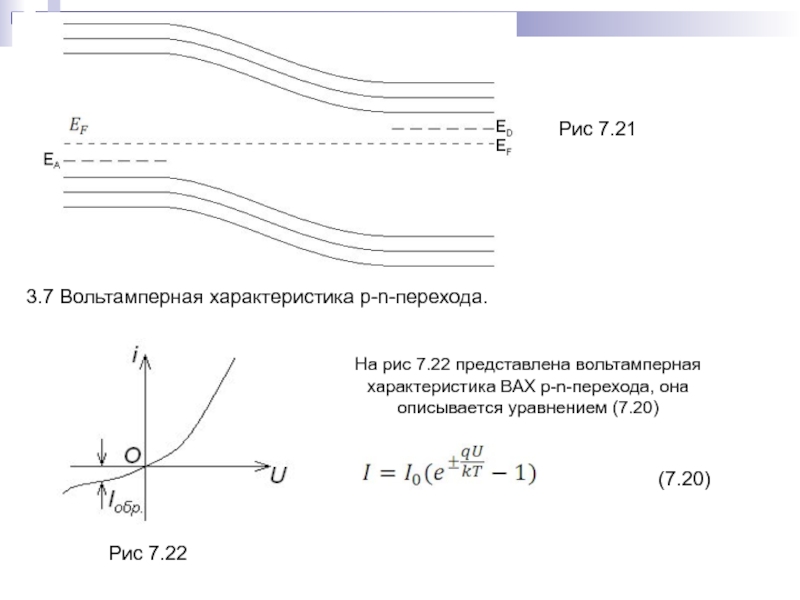
- 166. Рис 7.21Рис 7.22(7.20)3.7 Вольтамперная характеристика p-n-перехода.На рис
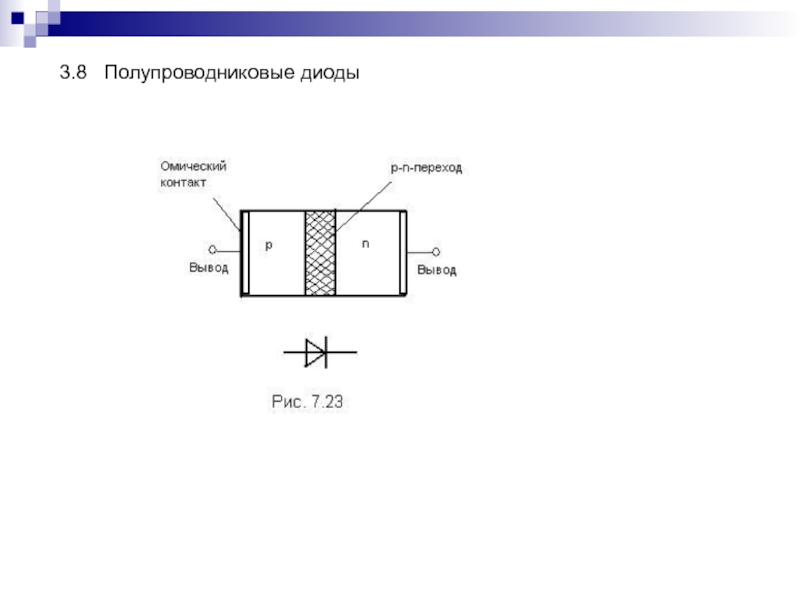
- 167. 3.8 Полупроводниковые диоды
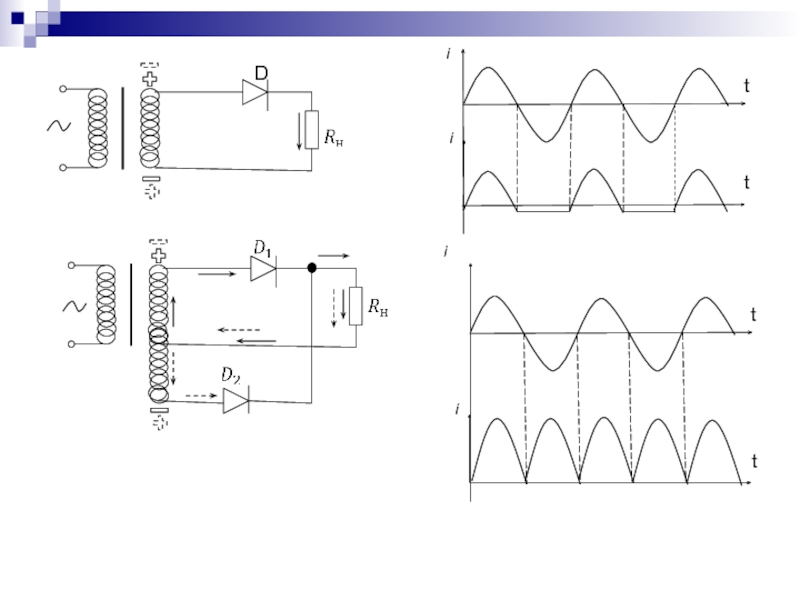
- 168. Diittitti
- 169. VIII.ОПТИКАВ оглавление
- 170. 1. Геометрическая оптика.§1. Закон прямолинейного распространения света.§2. Закон независимости световых лучей.Рис. 8.1Рис. 8.2Рис. 8.3С
- 171. §3. Закон отражения света.Рис. 8.5Рис. 8.4(8.1)α∆∆АВС=∆ADC, т.
- 172. §4. Закон преломления света.Рис. 8.6(8.3)(8.2)Пусть , тогда AD
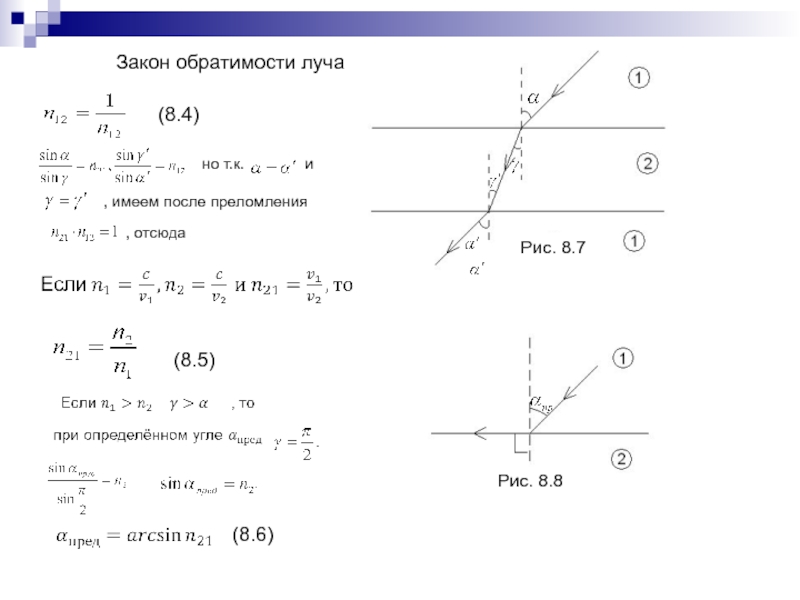
- 173. (8.4)(8.5)
- 174. §5 . Линзы.Рис. 8.9(8.8)(8.7)dесли поверхность выпуклая, R>0 если поверхность вогнутая, R
- 175. Рис. 8.10(8.9)(8.11)(8.12)(8.10)(8.13)В системе СИ D измеряется в
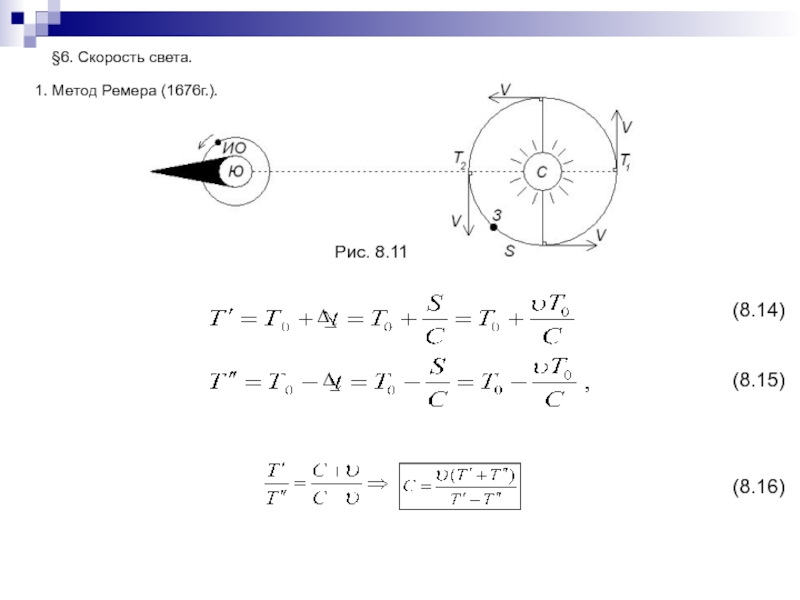
- 176. §6. Скорость света.1. Метод Ремера (1676г.).Рис. 8.11(8.16)(8.15)(8.14)∆∆
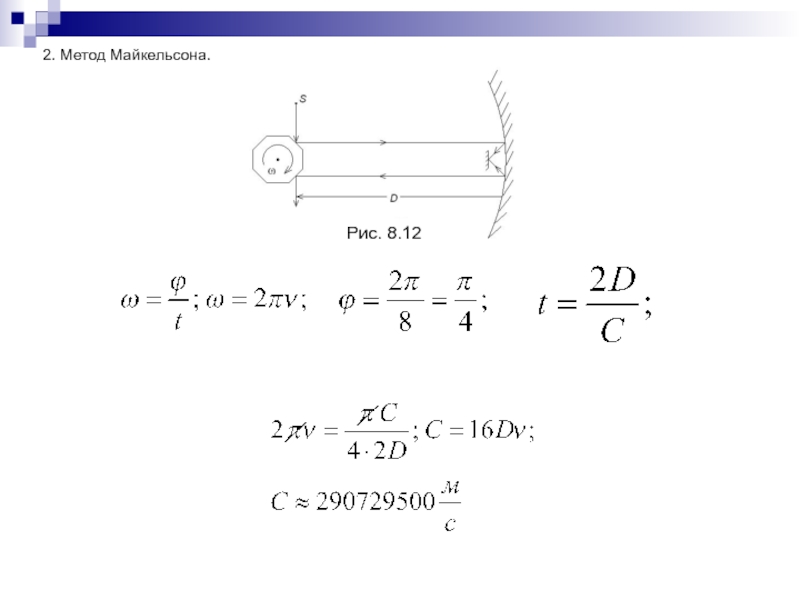
- 177. 2. Метод Майкельсона.Рис. 8.12
- 178. 2. Интерференция света. §1. Интерференция световых волн.Рис. 8.13(8.17)(8.18)(8.19)(8.20)(8.21)
- 179. §2. Способы наблюдения интерференции.1) Зеркало Френеля.Рис. 8.14(8.22)Если ∆
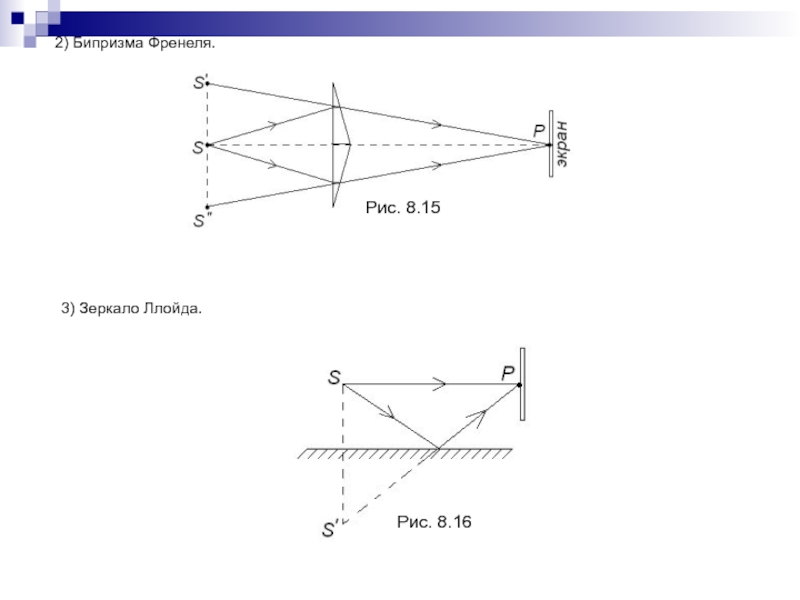
- 180. 2) Бипризма Френеля.3) Зеркало Ллойда.Рис. 8.15Рис. 8.16
- 181. §3. Интерференция света при отражении от тонких пластин.Рис. 8.17(8.24)(8.23)(8.25)Т.к.иb
- 182. §4. Полосы равного наклона и равной толщины.а) Полосы равного наклона.-12-б) Полосы равной толщины.Рис. 8.18Рис. 8.19линза
- 183. §5. Кольца Ньютона.Рис. 8.20Рис. 8.21(8.29)(8.28)(8.27)(8.26)отсюда
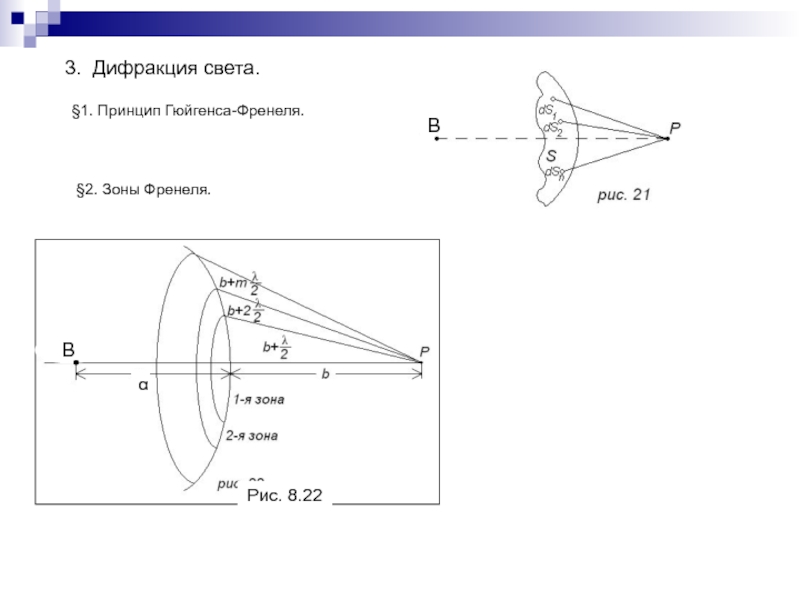
- 184. §2. Зоны Френеля.Рис. 8.22αВ3. Дифракция света.§1. Принцип Гюйгенса-Френеля.В
- 185. (8.31)(8.32)(8.33)(8.35)(8.38)(8.37)(8.36)α-xВРис. 8.23α3
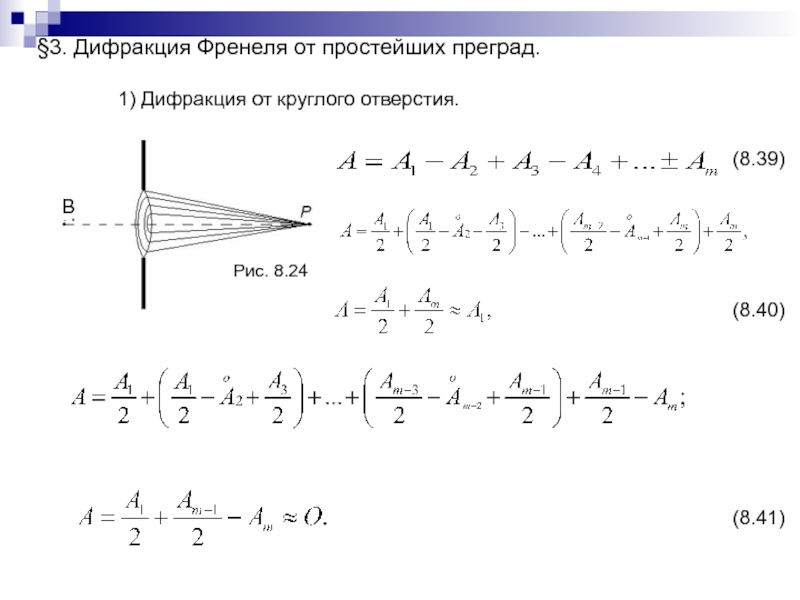
- 186. §3. Дифракция Френеля от простейших преград.1) Дифракция от круглого отверстия. -16-Рис. 8.24(8.39)(8.40)(8.41)В
- 187. 2) Дифракция от круглого диска.Рис. 8.25В
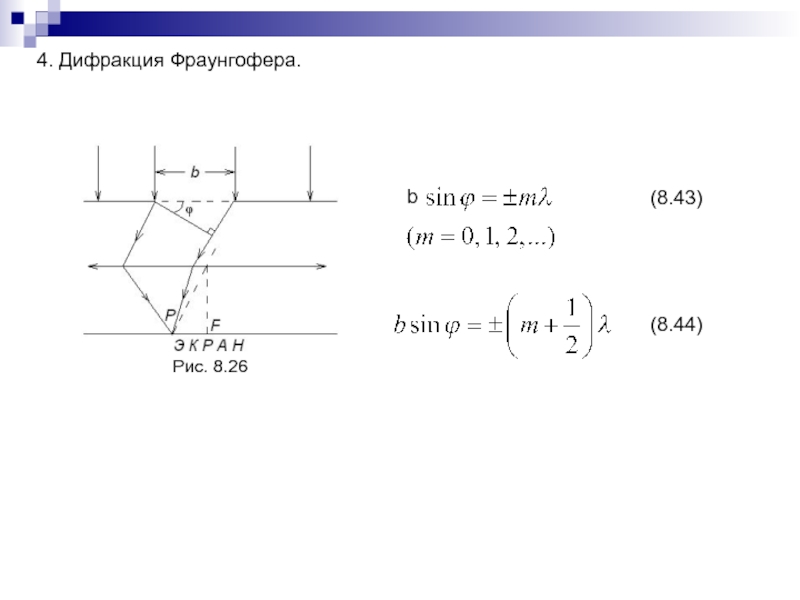
- 188. 4. Дифракция Фраунгофера.Рис. 8.26(8.43)(8.44)b
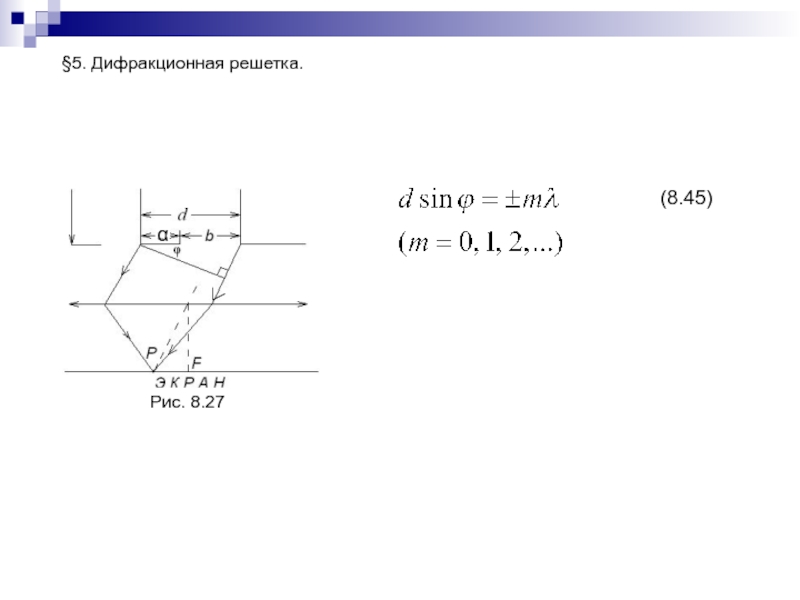
- 189. §5. Дифракционная решетка.Рис. 8.27(8.45)α
- 190. 4. Поляризация света. §1. Естественный и поляризованный свет.Рис. 8.28Рис. 8.29Рис. 8.30Естественный светЧастично поляризованныйПлоскополяризованный
- 191. §2. Поляризация при прохождении света через кристаллы.Рис. 8.31(8.47)(8.46)2∆ ∆
- 192. §3. Поляризация при отражении и преломлении света.§4. Жидкокристаллические индикаторы.Рис. 8.32Рис. 8.33(8.48)
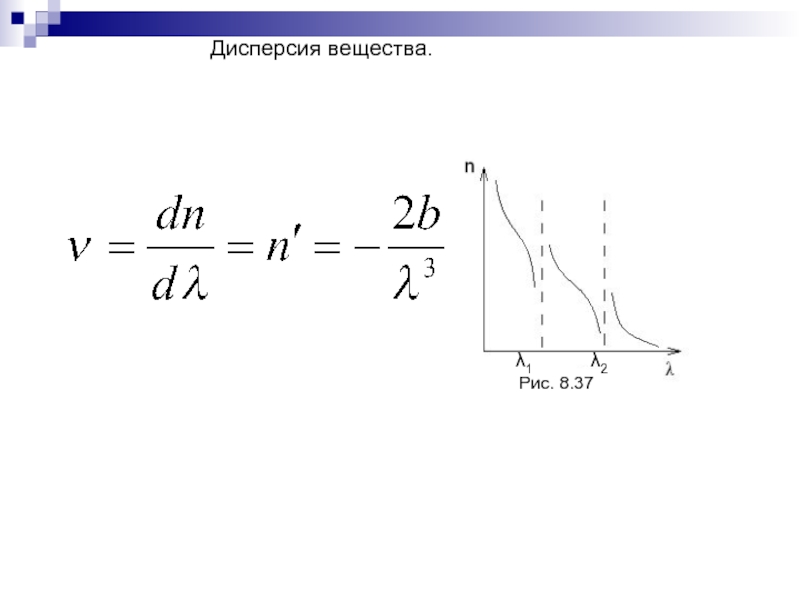
- 193. 5. Дисперсия света.§1. Сущность явления.(8.49)(8.50)
- 194. Рис. 8.35Рис. 8.36(8.51)(8.52)§2. Нормальная и аномальная дисперсия.Рис. 8.34
- 195. Рис. 8.37λ1λ2Дисперсия вещества.
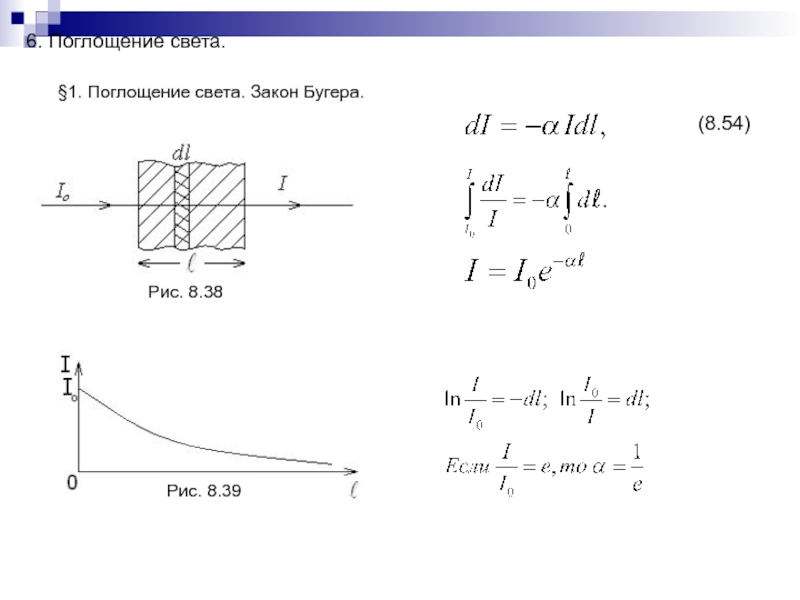
- 196. 6. Поглощение света. §1. Поглощение света. Закон Бугера.Рис. 8.38(8.54)Рис. 8.39
- 197. IX.АТОМНАЯ И ЯДЕРНАЯ ФИЗИКАВ оглавление
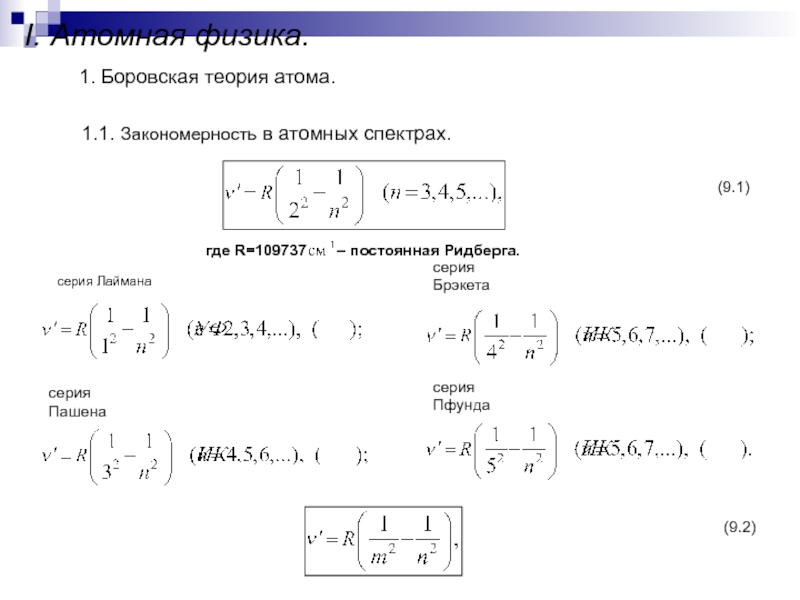
- 198. I. Атомная физика.1. Боровская теория атома.1.1. Закономерность в атомных спектрах.(9.1)серия Пфунда (9.2)
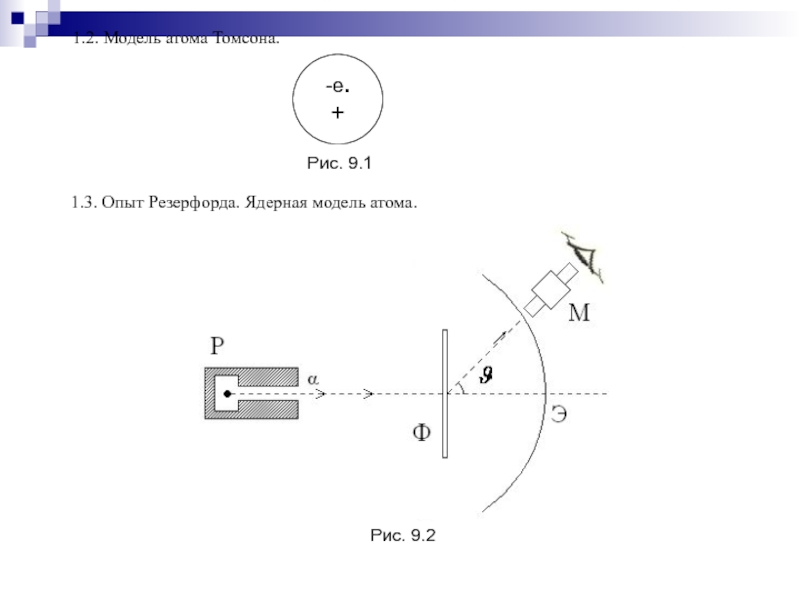
- 199. 1.2. Модель атома Томсона.1.3. Опыт Резерфорда. Ядерная модель атома.Рис. 9.1Рис. 9.2
- 200. 1.4. Постулаты Бора.(9.3)(9.4)(9.5)(9.6)1.5 Элементарная боровская теория атома
- 201. (9.7)(9.9)Рис. 9.3(9.11)(9.10)
- 202. 1.6 Опыт Франка и ГерцаРис 9.3Рис 9.2
- 203. 2. Ядерная физика.2.1. Состав и характеристика атомного
- 204. 2.2. Масса и энергия связи ядра.(9.13)Величина называется дефектом массы ядра.2.3. Радиоактивность.(9.15)(9.16)(9.17)(9.18)
- 205. Имеется три вида радиоактивных излучений: α-лучи, β-лучи,
- 206. 2.4. Ядерные реакции.(9.21)Примеры первых ядерных реакций:2.5. Деление ядер. Осколки претерпевают превращения:2.6. Термоядерные реакции.ss
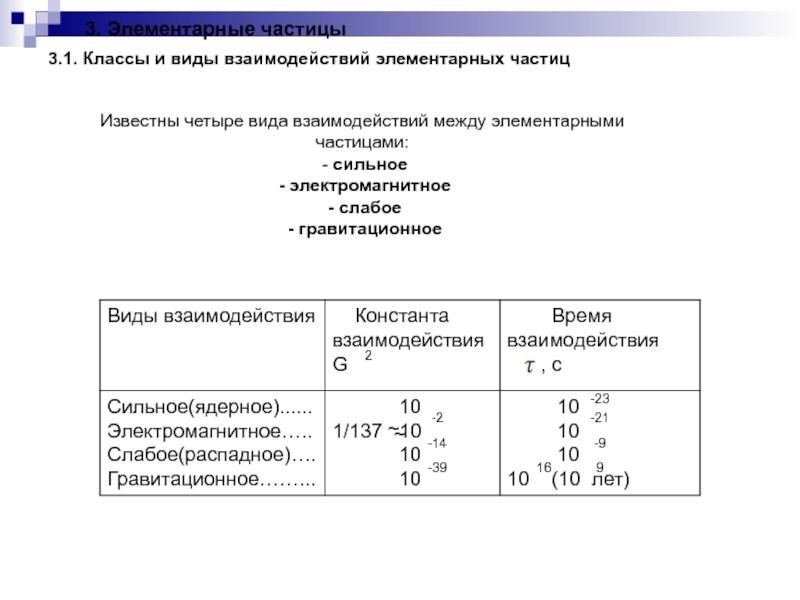
- 207. 3. Элементарные частицы3.1. Классы и виды взаимодействий
- 208. Элементарные частицы делятся на четыре класса.1.Фотоны,
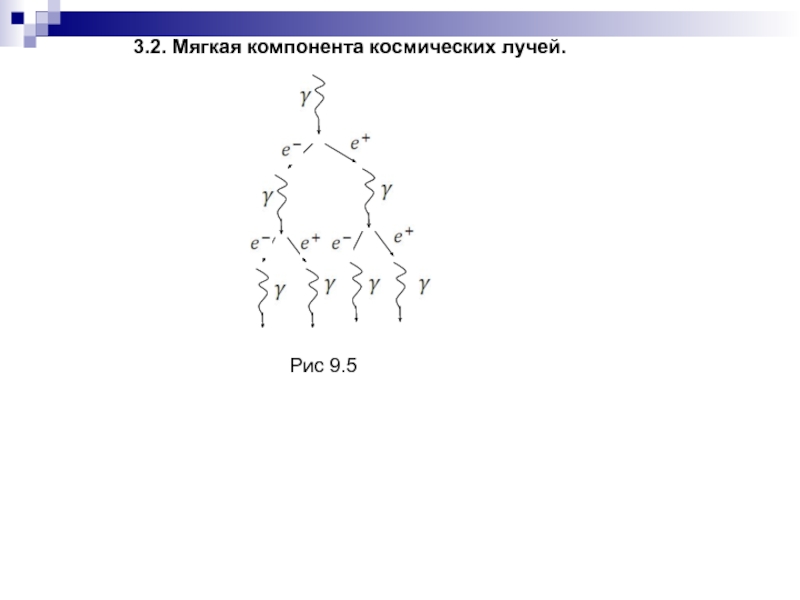
- 209. 3.2. Мягкая компонента космических лучей.Рис 9.5
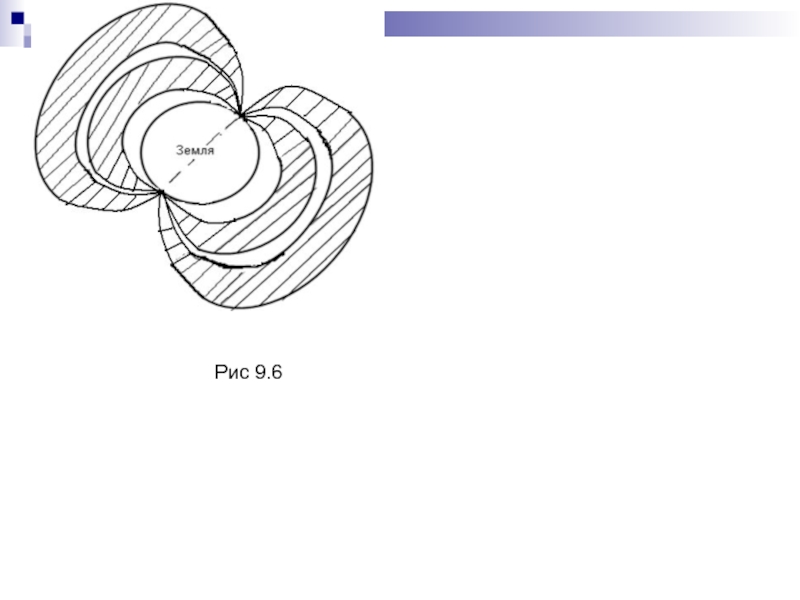
- 210. Рис 9.6
- 211. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Оглавление.
Механика
Молекулярная физика и термодинамика
Электростатика
Постоянный ток
Магнетизм
Электрические колебания
Квантовая физика
Оптика
Атомная и ядерная физика
Слайд 41.Кинематика
1.1Скорость
= элементарный путь.
- элементарное перемещение.
Скорость – производная
радиуса вектора
движущийся точки
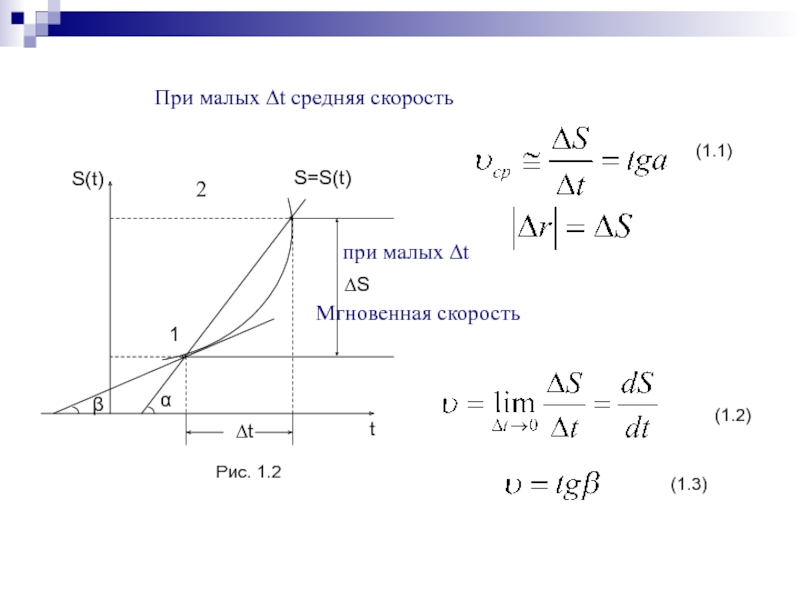
Слайд 5 При малых ∆t средняя скорость
2
при малых ∆t
Мгновенная скорость
t
S(t)
β
α
∆t
∆S
S=S(t)
Рис. 1.2
(1.3)
(1.2)
(1.1)
1
Слайд 81.4. Ускорение при криволинейном движении
Где единичный вектор
Нормальное ускорение показывает изменение вектора скорости по направлению.
Тангенсальное ускорение изменение линейной скорости по величине. (рис.1.5).
Полное ускорение:
0
Рис. 1.5
(1.10)
(1.11)
(1.12)
;
;
;
;
Слайд 91.5. Кинематика вращательного движения
Угловая скорость есть изменение угла
поворота тела за единицу времени- средняя угловая скорость
- мгновенная угловая скорость
- среднее угловое ускорение
Рис. 1.6
(1.13)
(1.14)
(1.15)
(1.16)
(1.17)
(1.18)
(1.19)
;
Слайд 102. Динамика материальной точки
2.1 Первый закон Ньютона
Всякое тело сохраняет
состояние покоя или равномерного прямолинейного движения до тех пор, пока
воздействие других тел не выведет его из этого состояния (на практике ΣF=0). Система отсчёта, относительно которой выполняется 1-й закон Ньютона, называется инерциальной (а если не выполняется, то – неинерциальной).Инерциальная система отсчёта – гелиоцентрическая система отсчёта.
Любая система отсчёта, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, будет инерциальной.
Слайд 11
2.2 Второй закон Ньютона
2.3Третий закон Ньютона
Сила действия равна силе противодействия
Основное уравнение классической механики.
- импульс.
Второй
закон Ньютона в дифференциальной форме. (1.20)
(1.21)
(1.22)
(1.23)
Слайд 122.4 Закон сохранения импульса
2.5 Принцип относительности Галилея
Отсчет времени производится с того момента,
когда совпадает с .Найдем связь между координатами систем.
1
2
Это преобразования Галилея .
1.
Продиф-ференцируем 1.
2.
3.
Правило сложения скоростей
в классической механике
Рис. 1.7
Рис. 1.8
(1.24)
(1.25)
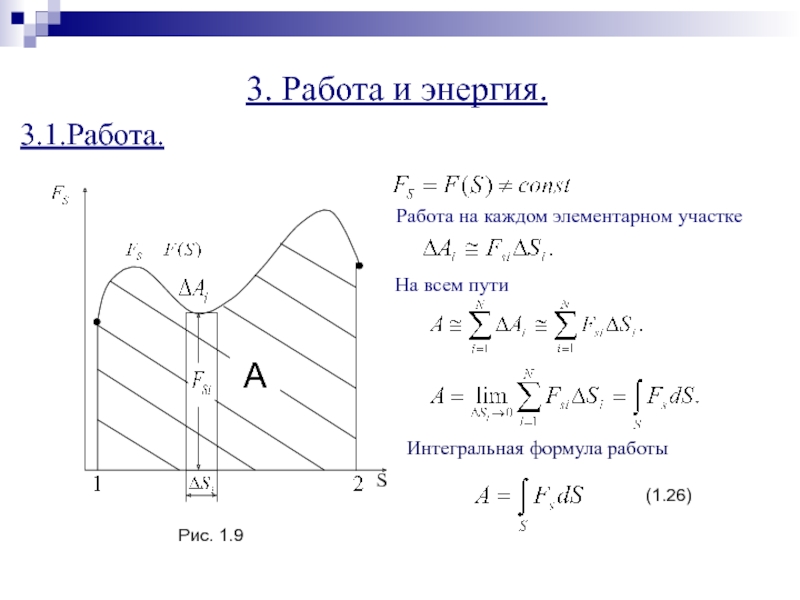
Слайд 133. Работа и энергия.
3.1.Работа.
S
A
Работа на каждом элементарном участке
На всем пути
Рис.
1.9
(1.26)
Интегральная формула работы
Слайд 143.2. Мощность.
Мощность - работа механизма за единицу времени.
3.3. Энергия.
Энергия –
физическая величина, характеризующая способность тела и системы тел совершать работу.
3.4.
Кинетическая энергия.- средняя мощность
Мгновенная мощность
Мощность- скалярное произведение и .
.
Работа-мера
измерения
кинетической
энергии
(1.27)
(1.28)
(1.29)
(1.30)
Слайд 153.5. Потенциальная энергия.
3.6. Закон сохранения энергии.
Внутри замкнутой системы действуют конc. силы.
Рис. 1.10
(1.31)
(1.32)
(1.33)
(1.34)
1
2
dh
;
;
;
;
Слайд 164. Центральный удар шаров.
4.1. Абсолютно упругий удар и неупругий удары.
а)
Абсолютно упругий удар.
Затем вычтем из (1.36) (1.39)
Умножая (1.38) на m1, имеем
Рис. 1.10
(1.40)
Отсюда определим
Слайд 17
б) Абсолютно неупругий удар.
Затем (1.41) + (1.36)
Если шары
движутся на
встречу друг другу, то 0,
а 0 , тогда
Для численных подсчетов
«-» - тела движутся на встречу
«+» - тела движутся в одну сторону
Пр №№ 2.89, 2.90
(1.42)
(1.43)
(1.41)
Слайд 185. Динамика вращательного движения.
5.1. Момент силы относительно точки.
;
, где
плечо силы относительно точки 0.
, т.к. они коллинеарны. (sinπ=0)
т.к.
,то
Момент суммы сил, имеющих общую точку приложения, равен сумме мом. слагаемых сил.
Рис. 1.12
(1.44)
(1.45)
Слайд 195.2. Момент силы относительно оси.
5.3. Момент инерции.
Физическая величина
, равная сумме произведений масс материальных точек на квадраты их расстояний от оси Z, называются моментом инерции системы относительно оси Z.
Вектор
, следовательно
Отсюда
т.к.
,то
Рис. 1.13(а)
(1.46)
(1.47)
Рис. 1.13(б)
Слайд 20
Момент инерции J относительно произвольной оси равен сумме момента инерции
Jc относительно оси, параллельной данной и проходящей через центр инерции*
тела, и произведения массы тела m на квадрат расстояния a между осями.*Назовем центром инерции системы точку, положение которой в пространстве
задается радиусом-вектором . Декартовы координаты центра инерции равны проекциям на координатные оси:
(1.48)
5.4. Теорема Штейнера.
Слайд 21
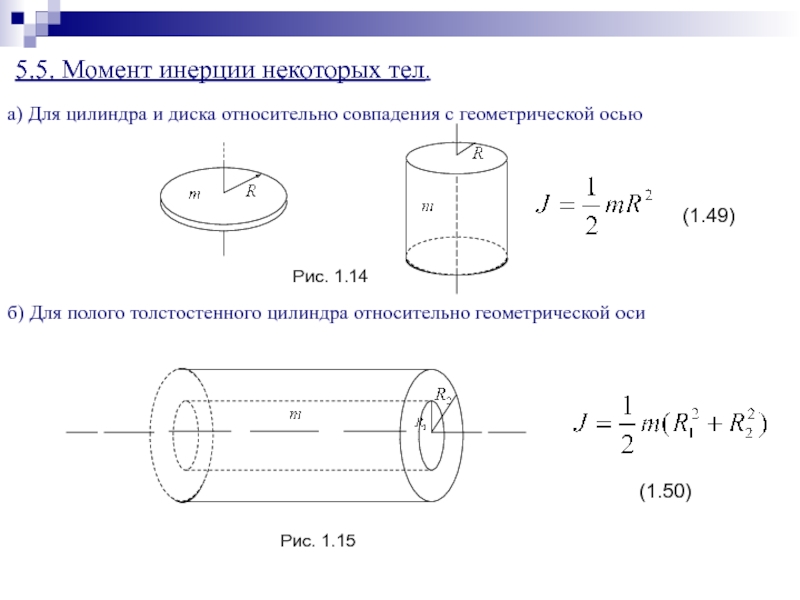
а) Для цилиндра и диска относительно совпадения с геометрической осью
б)
Для полого толстостенного цилиндра относительно геометрической оси
Рис. 1.14
Рис. 1.15
(1.49)
(1.50)
5.5. Момент
инерции некоторых тел.Слайд 22в) Для шара относительно оси, проходящей через центр
г) Для материальной
точки
д) Для тонкого стержня относительно оси, проходящей через середину стержня
и перпендикулярной ему.Если ось проходит через конец стержня, то по теореме Штейнера:
Рис. 1.16
Рис. 1.17
(1.51)
(1.52)
(1.53)
(1.54)
Слайд 235.6. Основной закон динамики вращательного движения.
Для всего абсолютно твердого тела
Рис.
1.19
(1.55)
Слайд 24
а) Для материальной точки.
б) Для твердого тела.
в) Для замкнутой системы
тел (
) суммарный момент импульса постоянен.(1.56)
(1.57)
(1.59)
(1.60)
(1.58)
;
;
5.7. Момент импульса. Закон сохранения момента импульса.
Слайд 275.10. Кинетическая энергия тела при плоских движениях.
Кинетическая энергия i-ой элем.
массы равна
(1.62)
;
Слайд 286. Колебательное движение
6.1 Гармонические колебания.
Колебания, происходящие по закону синуса или
косинуса, называются гармоническими.
Рассмотрим пружинный маятник (рис.1.21(а))
Из 2-го закона Ньютона:
Следовательно,
движение системы под действием - гармоническое колебание.
А - амплитуда колебаний;
- фаза колебаний
- начальная фаза колебаний
t =0,
- начальное смещение;
, то
Рис. 1.21(а)
Рис. 1.22
(1.63)
(1.64)
(1.65)
Общее решение уравнения имеет вид
Слайд 30 Число колебаний в единицу времени называется частотой колебания
(Гц):
- собственная циклическая частота.
- число колебаний за секунд.опережает на .
и находятся в противофазе.
(1.67)
(1.66)
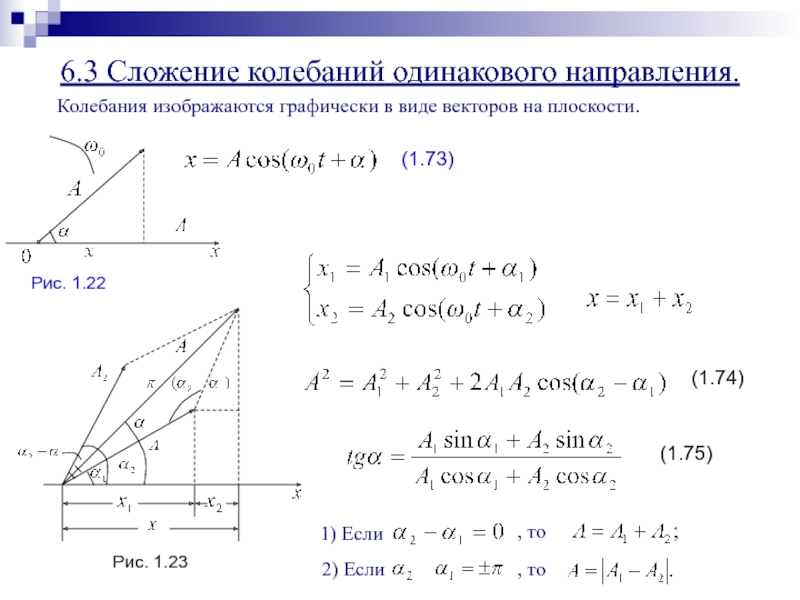
Слайд 336.3 Сложение колебаний одинакового направления.
Колебания изображаются графически в виде векторов
на плоскости.
(1.73)
(1.74)
(1.75)
Слайд 346.4. Сложение взаимноперпендикулярных колебаний.
Частоты определяются первого колебания:
а) одинаковая частота
1)
2)
3)
Рис. 1.24
(1.76)
второго колебания:
Слайд 366.5. Затухающие колебания
и
Решение уравнения (1) будем искать в виде
Продифференцируем (2)
по t и найдем и
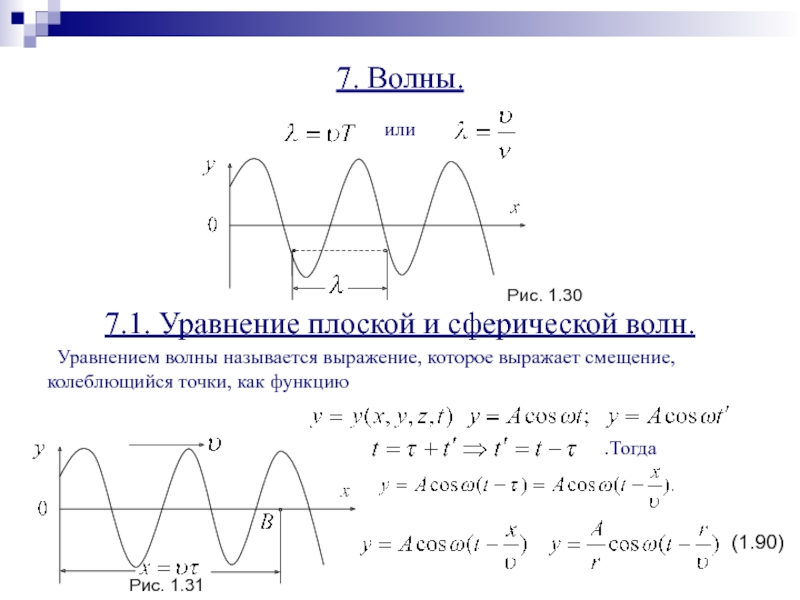
Слайд 417. Волны.
7.1. Уравнение плоской и сферической волн.
Уравнением волны называется выражение,
которое выражает смещение, колеблющийся точки, как функцию
или
.Тогда
Рис. 1.30
Рис. 1.31
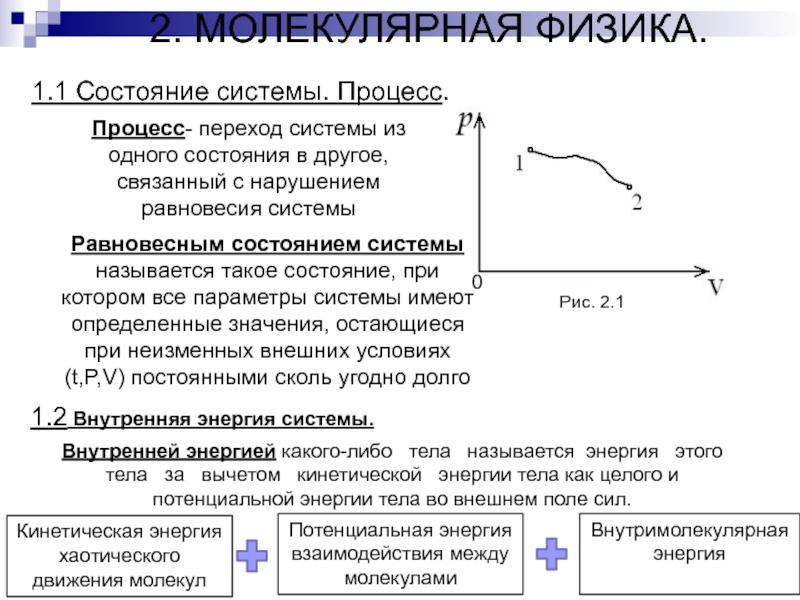
(1.90)Слайд 431.1 Состояние системы. Процесс.
Рис. 2.1
2. МОЛЕКУЛЯРНАЯ ФИЗИКА.
Равновесным состоянием системы называется
такое состояние, при котором все параметры системы имеют определенные значения,
остающиеся при неизменных внешних условиях (t,P,V) постоянными сколь угодно долгоПроцесс- переход системы из одного состояния в другое, связанный с нарушением равновесия системы
1.2 Внутренняя энергия системы.
Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил.
Кинетическая энергия хаотического движения молекул
Потенциальная энергия взаимодействия между молекулами
Внутримолекулярная энергия
0
Слайд 441.3 Температура.
1.4 Уравнение состояния идеального газа.
(2.3)
(2.2)
(2.1)
Соотношение, дающее связь между
параметрами какого-либо тела, называется уравнением состояния этого тела
Слайд 45Закон Гей-Люссака.
Закон Бойля-Мариотта.
Закон Шарля.
(V=const). Изохорный процесс.
(2.4)
(2.6)
(2.5)
(P=const). Изобарный процесс.
P1V1=P2V2
(T=const).
Изотермический процесс
Слайд 47где В – постоянная для данной массы газа величина.
(2.7)
(2.8)
(2.9)
(2.10)
- Уравнение
Клайперона
- уравнение Менделеева-Клайперона
Слайд 481.5 Уравнение кинетической теории газов для давления.
(2.11)
(2.12)
(2.13)
(2.14)
- постоянная Больцмана
Слайд 491.6 Распределение молекул газа по скоростям.
Функция распределения молекул по
скорости была найдена теоретически Максвеллом и носит его имя. Она
имеет следующий вид:(2.15)
где А – множитель, не зависящий от υ
m – масса молекулы,
k – постоянная Больцмана
Слайд 512. ОСНОВЫ ТЕРМОДИНАМИКИ
(2.16)
(2.18)
(2.17)
Уравнение (2.18) выражает закон сохранения энергии и представляет
собой содержание первого закона (начала) термодинамики
2.1 Первое начало термодинамики.
Слайд 53(2.19)
(2.20)
(2.21)
(2.22)
(2.23)
Складывая уравнения (2.19) и (2.20), получаем:
Тепловую машину принято характеризовать коэффициентом
полезного действия η (сокращенно к. п. д.),
К.П.Д. не может быть
больше единицы.Слайд 542.3 Второе начало термодинамики.
Второе начало термодинамики, как и первое, может
быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало
гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.Второе начало может быть также сформулировано следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла полностью в работу.
Слайд 561. Электрическое поле в вакууме.
1.2 Взаимодействие зарядов. Закон Кулона.
Рис. 3.1
1.1 Введение
.
Слайд 581.4 Линии напряженности. Поток вектора напряженности.
; т.к.
Рис. 3.3
E
En
α
α
;
Если
, то
, а если
:
(3.5)
(3.4)
Слайд 611.6 Применение теоремы Гаусса.
1) Поле бесконечной однородно заряженной плоскости.
Рис. 3.6
(3.10)
;
;
;
;
Слайд 622) Поле двух равномерно и разноименно заряженных бесконечных плоскостей.
+ s
–
s
3) Поле бесконечного заряженного цилиндра.
Рис. 3.7
Рис. 3.8
(3.11)
(3.12(а)
ε0
ε0
+
E(r)=0
(3.12(б)
;
;
;
;
Слайд 63
4) Поле заряженной сферической поверхности.
5) Поле объемно заряженной сферы.
Рис.
3.9
Рис. 3.12
Рис. 3.10
Рис. 3.11
(3.13)
(3.15)
(3.14)
Если
, то
,
;
;
;
Слайд 65B СИ и U измеряется в Вольтах:
(3.19)
(3.21)
(3.20)
ε0
ε0
ε0
;
;
1.8 Потенциал.
Разность потенциалов.
(3.18)
ε0
.
Слайд 682. Электрическое поле в диэлектриках.
2.1 Полярные и неполярные молекулы.
Рис. 3.20
Рис. 3.21
Рис. 3.19
(3.26)
(3.25)
ε0
+q
-q
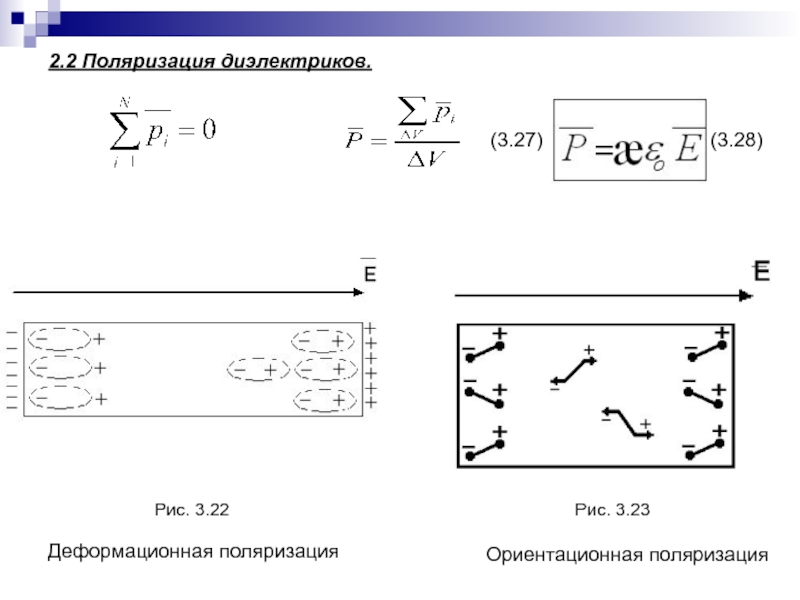
Слайд 692.2 Поляризация диэлектриков.
Деформационная поляризация
Ориентационная поляризация
Рис. 3.23
Рис. 3.22
(3.28)
(3.27)
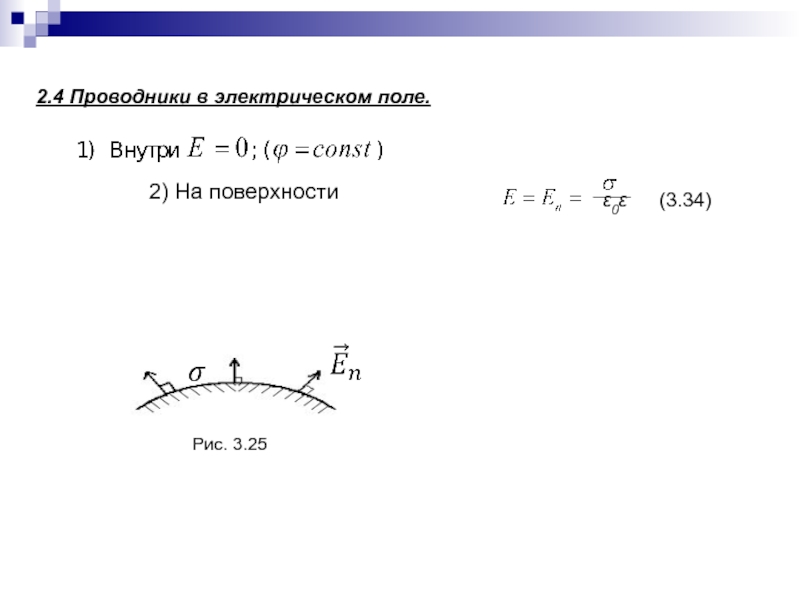
Слайд 722.5 Проводники во внешнем электрическом поле.
2.6 Электроемкость.
Рис. 3.26
(3.35)
ε
0 ε
ε0ε
ε0ε
(3.36)
ε0ε
ε0ε R
4π ε0ε R
4π ε0ε R
;
;
;
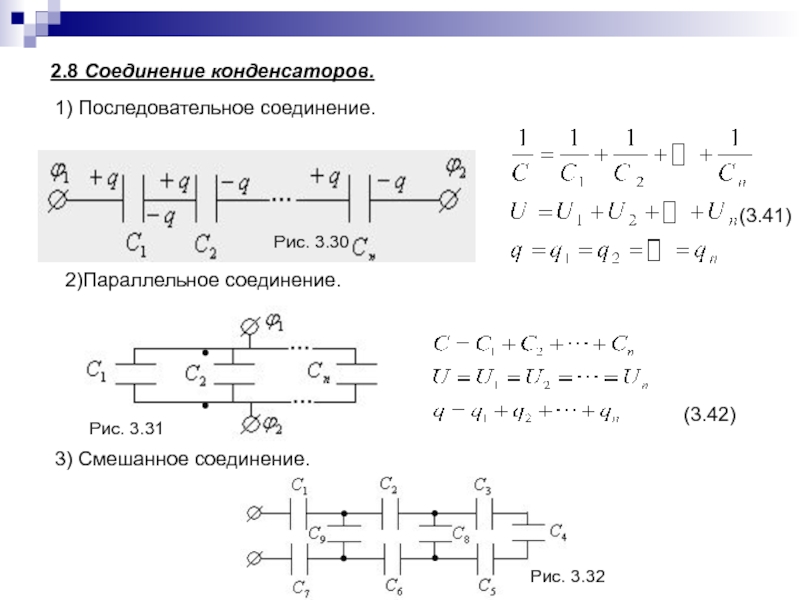
Слайд 76 2.8 Соединение конденсаторов.
Рис. 3.30
(3.41)
2)Параллельное соединение.
3) Смешанное соединение.
Рис. 3.31
Рис.
3.32
(3.42)
1) Последовательное соединение.
Слайд 824.1. Сила тока
Сила тока I есть физическая величина, численно
равная заряду, прошедшему через поперечное сечение проводника за единицу времени.
Если через поперечное сечение проводника проходят заряд Δq за время Δt, то сила тока равна.(4.1)
В системе СИ за единицу силы тока принимается ампер (А).
Слайд 83
Отсюда
тогда
Из рис 4.1 видно, что
, где
-
проекция j
на нормаль к площадке ΔS, откуда имеем:
Рис. 4.1
(4.4)
(4.3)
(4.5)
4.2. Вектор
плотности токагде Δq – заряд, прошедший через площадку за время Δt, j– плотность тока.
(4.2)
(4.6)
;
В системе СИ вектор плотности тока
измеряется в Амперах на квадратный метр, т.е.
Слайд 84
4.3. Закон Ома для однородного участка цепи.
Сопротивление проводников.
I=f(U)
I=kU
Обозначим сопротивление через R, тогда
или
(4.7)
(4.8)
Где ρ - удельное сопротивление проводника;
l - длина проводника;
S - площадь его поперечного сечения.
(4.11)
(4.10)
(4.9)
В системе СИ сопротивление измеряется в Омах.
Слайд 85где
- сопротивление этого участка.
Подставляя в равенство (4.12) последнее
равенство, имеем:
Но так как
и
, имеем
j=σE
или
в векторном видеРис. 4.2
(4.13)
(4.14)
(4.15)
(4.12)
4.4. Закон Ома в дифференциальной форме.
Слайд 864.5. Электродвижущая сила.
Закон Ома для замкнутой цепи.
Применим закон Ома для внутреннего
участка цепи, т.е.
Обозначим скачки потенциалов
через и :
Рис. 4.3
(4.16)
(4.17)
Слайд 87тогда имеем
или
Закон Ома для замкнутой цепи.
, получим из формулы (4.19):
Заметив, что
Если I=0, т.е. цепь разомкнута, то
а это значит,
что электродвижущая сила есть величина, численно равная разности потенциалов на зажимах разомкнутого элемента.
(4.18)
(4.19)
(4.20)
(4.21)
(4.22)
(4.24)
(4.23)
Если q=+1, то ε=A, т.е. ЭДС источника есть величина, численно равная работе, совершаемой при перемещении единицы заряда по замкнутой цепи.
(4.25)
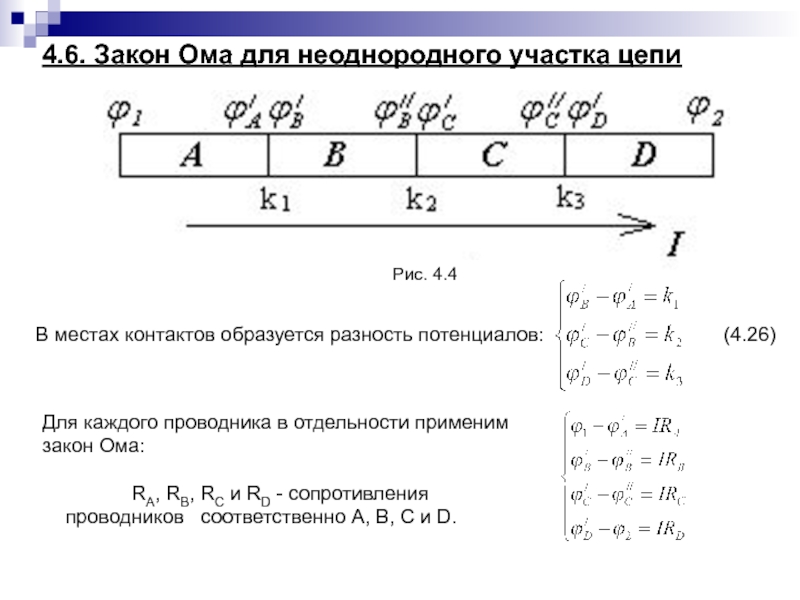
Слайд 884.6. Закон Ома для неоднородного участка цепи
Рис. 4.4
В местах
контактов образуется разность потенциалов:
(4.26)
Для каждого проводника в отдельности применим
закон Ома:
RA, RB, RC и RD - сопротивления проводников соответственно A, B, C и D.
Слайд 89Складывая последние равенства, найдем:
Здесь
где ε - ЭДС, действующая на данном
неоднородном
участке.
Полное сопротивление участка R:
R=RA+RB+RC+RD
или
Это и
есть закон Ома для неоднородного участка цепи. (4.27)
(4.28)
(4.30)
(4.29)
Слайд 90Этот закон является наиболее общим законом Ома, и из него
легко получить два других.
Для однородного участка цепи:
Слайд 914.7. Мощность, выделяемая в цепи.
Но так как по закону
Ома для замкнутой цепи
, то
(4.31)
Т.к. по закону Ома
то полную
мощность можно выразить через внешнее сопротивление, исходя из формулы(4.31)
(4.32)
Полная мощность имеет наибольшее значение при токе
короткого замыкания, т.е. при R=0:
Рис. 4.5
Слайд 92Мощность, выделенная на внешнем участке цепи,
Pa равна:
R = r
Коэффициент полезного действия источника
Коэффициент полезного действия источника η есть
величина, численно равная отношению мощности,
выделенной на внешнем участке цепи, к полной
мощности:
(4.34)
(4.33)
(4.35)
Слайд 934.8. Закон Джоуля-Ленца.
Интегральная форма закона.
Если I изменяется со
временем, то
(4.39)
(4.38)
(4.37)
(4.36)
Слайд 944.9. Закон Джоуля-Ленца
в дифференциальной форме.
Плотность тепловой мощности:
Но так
как
и
, то, подставляя
последние два равенства в формулу
(4.40), получим: где
- плотность тока.
(4.41)
(4.40)
(4.43)
(4.42)
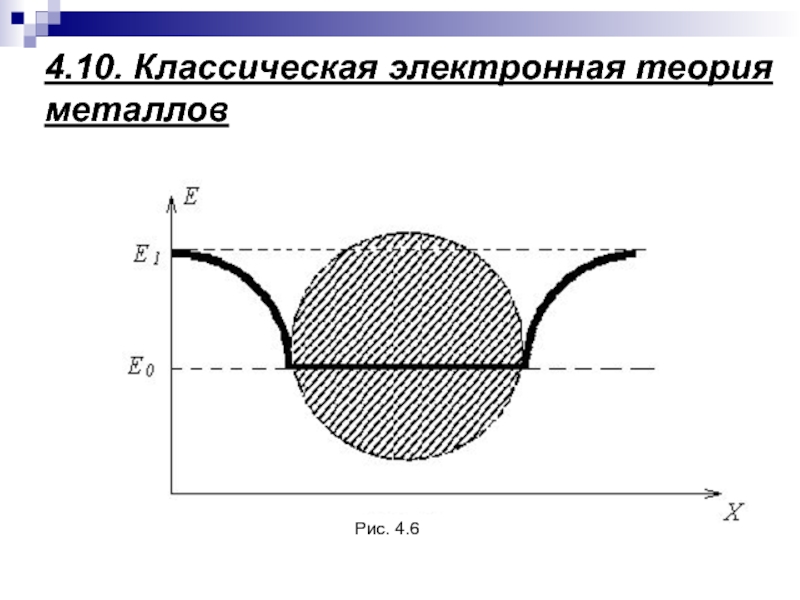
Слайд 964.11. Закон Ома с точки зрения
классической электронной теории
Как мы уже знаем плотность тока
где
q - переносимый заряд;S - площадь поперечного сечения проводника;
t - время переноса заряда.
где e - заряд электрона;
n0 - число электронов в единице объема.
(4.44)
(4.45)
Переносимый заряд равен:
Подставляя формулу (4.45) в (4.44), получим
(4.47)
(4.46)
Между столкновениями электрон движется равноускоренно, т.к. E=const, тогда
(4.48)
где a - ускорение электрона;
t - время между двумя столкновениями.
Слайд 97Где m - масса электрона.
(4.49)
По второму закону Ньютона:
- средняя
скорость беспорядочного теплового
движения, т.к. при обычных плотностях тока
(4.50)
Подставляя формулу
(4.49) и (4.50) в (4.48), а (4.48) в (4.47), получим окончательное выражение для средней скорости направленного движения(4.51)
(4.53)
(4.52)
(4.54)
Слайд 98Закон Джоуля-Ленца с точки зрения классической теории
Подсчитаем количество теплоты, выделенное
в единице
объема проводника за единицу времени.
К концу свободного пробега
электрон приобретает скорость
,как было показано выше, равную
Следовательно, кинетическая энергия, которую электрон
передаст решетке при одном столкновении, будет:
За единицу времени электрон столкнется Z раз.
Число столкновений:
(4.57)
(4.55)
(4.56)
Слайд 99Плотность тепловой мощности:
где
, окончательно имеем:
что является законом Джоуля-Ленца.
,
(4.58)
(4.59)
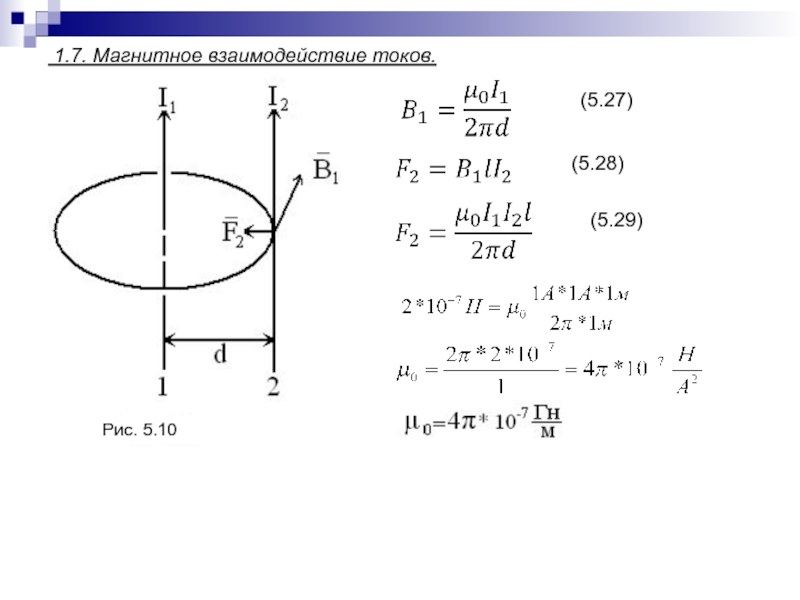
Слайд 104Применение закона Био-Савара-Лапласа.
Пример I. Магнитное поле прямого провода с током.
(5.9)
(5.10)
(5.11)
(5.12)
Слайд 107Пример 3. Магнитное поле на оси соленоида.
(5.15)
Для соленоида конечной длины
(короткий соленоид)
(5.16)
где α1 и α2 – углы между осью
соленоида и радиусом-вектором, проведенным из рассматриваемой точки к концу соленоида Рис. 5.6
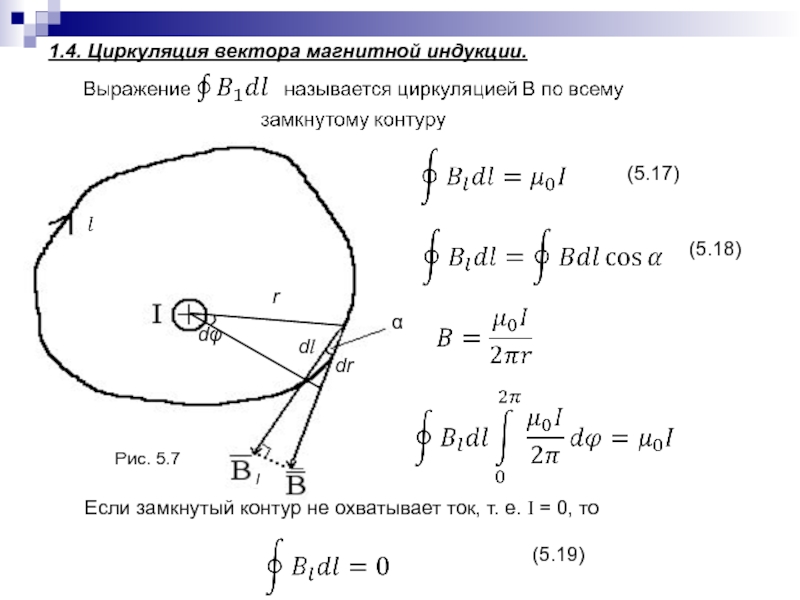
Слайд 1081.4. Циркуляция вектора магнитной индукции.
(5.17)
(5.18)
и dlcosα = rdφ
Рис. 5.7
dr
α
r
dl
l
dφ
Если
замкнутый контур не охватывает ток, т. е. I = 0,
то(5.19)
.
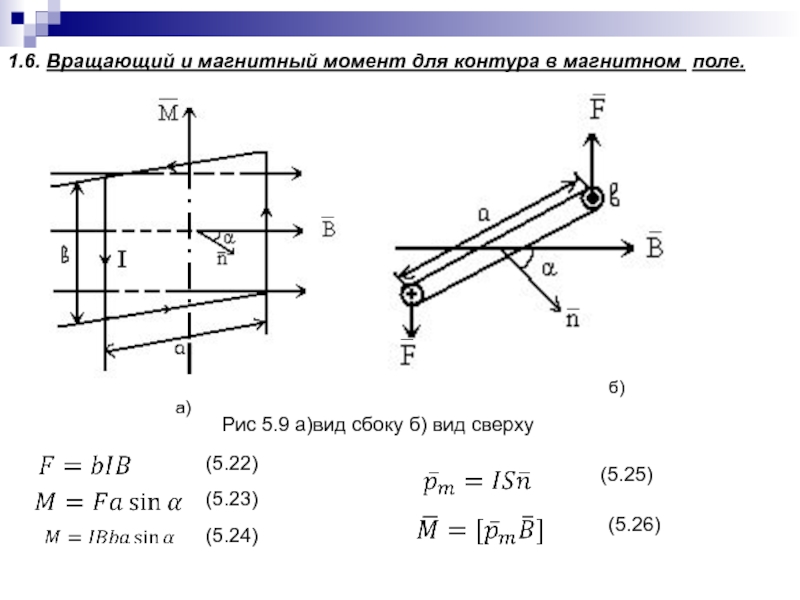
Слайд 1101.6. Вращающий и магнитный момент для контура в магнитном поле.
а)
б)
(5.22)
(5.23)
Рис 5.9 а)вид сбоку б) вид сверху
(5.24)
(5.25)
(5.26)
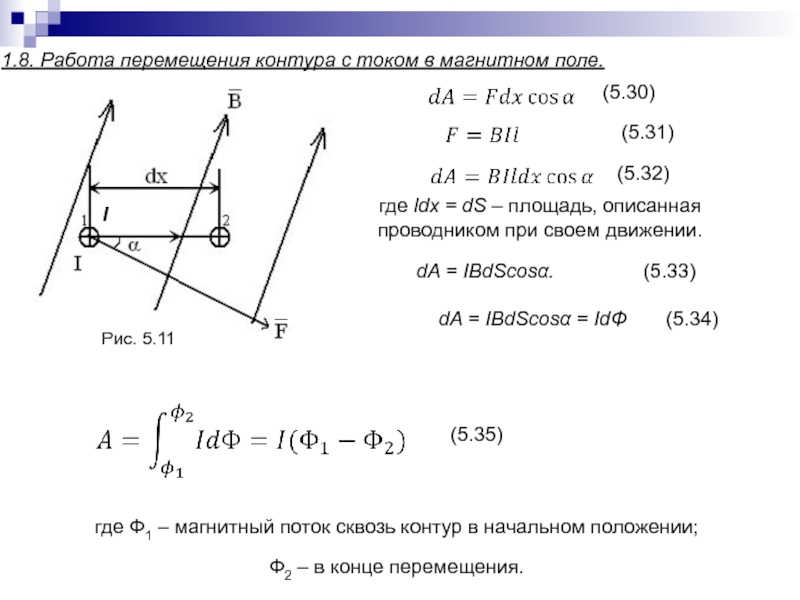
Слайд 1121.8. Работа перемещения контура с током в магнитном поле.
(5.30)
(5.31)
(5.32)
где ldx = dS – площадь, описанная
проводником при своем движении.
dA = IBdScosα. (5.33)
dA = IBdScosα = IdΦ (5.34)
(5.35)
где Ф1 – магнитный поток сквозь контур в начальном положении;
Ф2 – в конце перемещения.
Рис. 5.11
l
Слайд 1152.Магнитное поле в магнетиках.
2.1. Намагничивание веществ.
Вещества, способные намагничиваться,
называются магнетиками.
Вектор намагничивания есть величина численно равная суммарному магнитному
моменту, приходящемуся на единицу объема магнетика, т.е. (5.48)
Слайд 1162.2. Магнитное поле в магнетике. Вектор магнитной индукции.
B`=μ0ni= μ0j
(5.49)
(5.50)
(5.51)
(5.52)
(5.53)
(5.54)
(5.55)
или
где
(5.56)
(5.57)
Рис.
5.15Рис. 5.16
Слайд 118
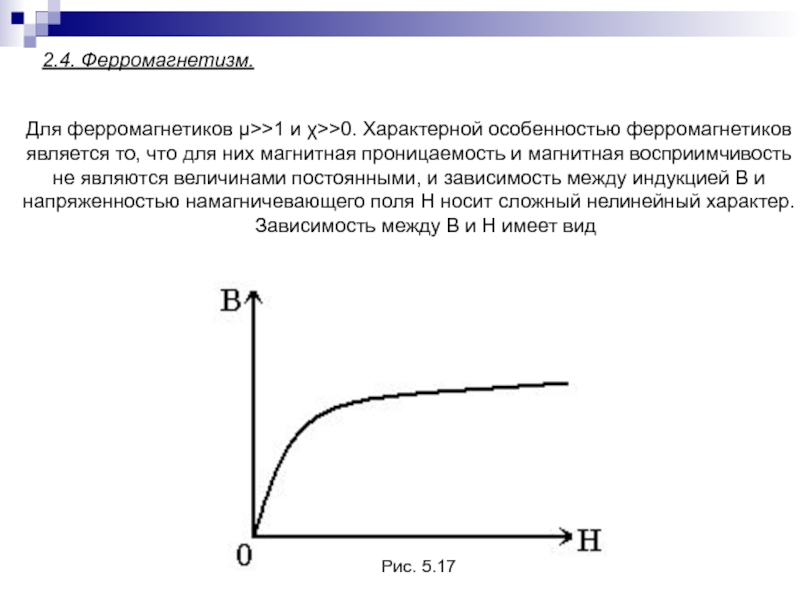
Для ферромагнетиков >>1 и >>0. Характерной особенностью ферромагнетиков является то,
что для них магнитная проницаемость и магнитная восприимчивость не являются
величинами постоянными, и зависимость между индукцией В и напряженностью намагничевающего поля Н носит сложный нелинейный характер.Зависимость между В и Н имеет вид
2.4. Ферромагнетизм.
Рис. 5.17
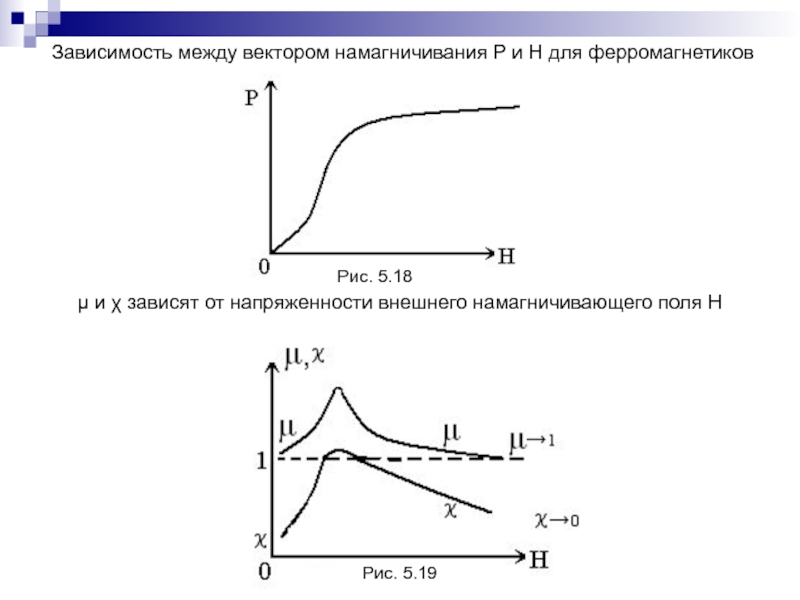
Слайд 119Зависимость между вектором намагничивания Р и Н для ферромагнетиков
и зависят от напряженности внешнего намагничивающего поля Н
Рис.
5.18Рис. 5.19
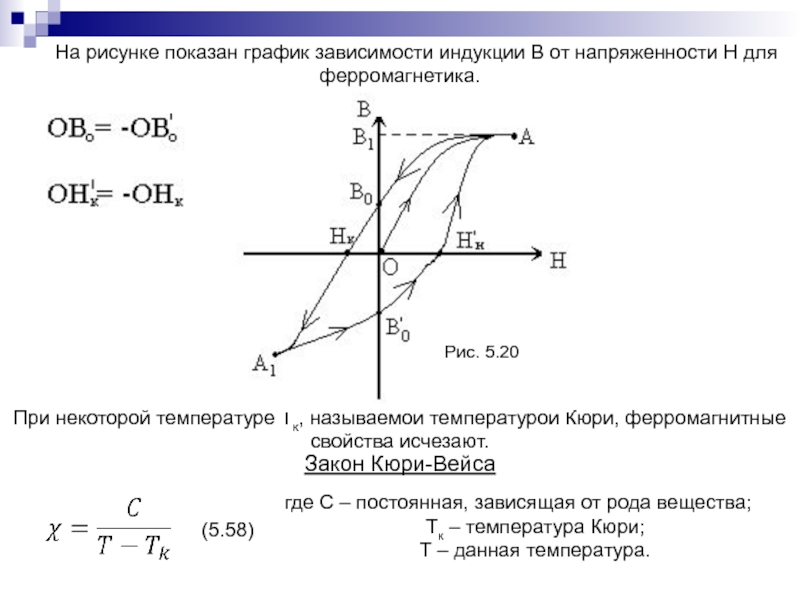
Слайд 120 На рисунке показан график зависимости индукции В
от напряженности Н для ферромагнетика.
При некоторой температуре Тк, называемой
температурой Кюри, ферромагнитные свойства исчезают. Закон Кюри-Вейса
где С – постоянная, зависящая от рода вещества;
Тк – температура Кюри;
Т – данная температура.
Рис. 5.20
(5.58)
Слайд 121 3. Электромагнитная индукция.
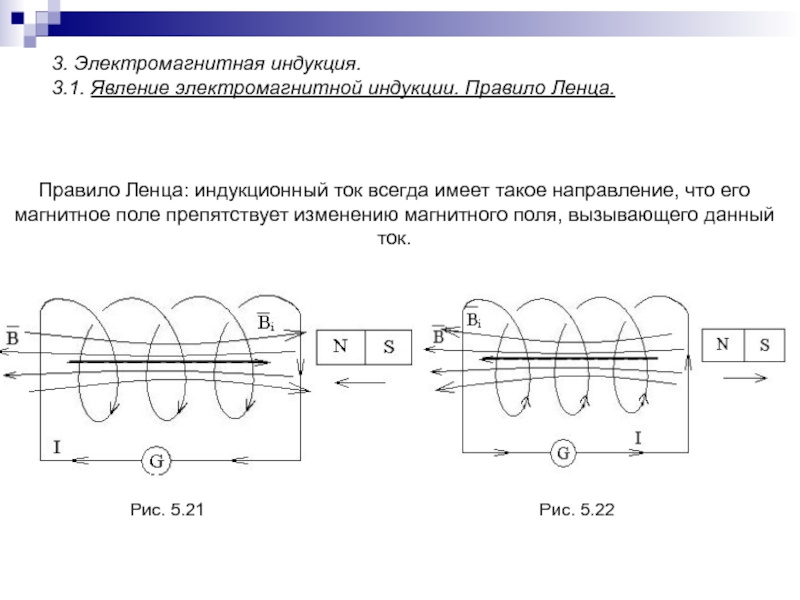
3.1. Явление электромагнитной индукции. Правило Ленца.
Правило Ленца: индукционный ток
всегда имеет такое направление, что его магнитное поле препятствует изменению магнитного поля, вызывающего данный ток.Рис. 5.21
Рис. 5.22
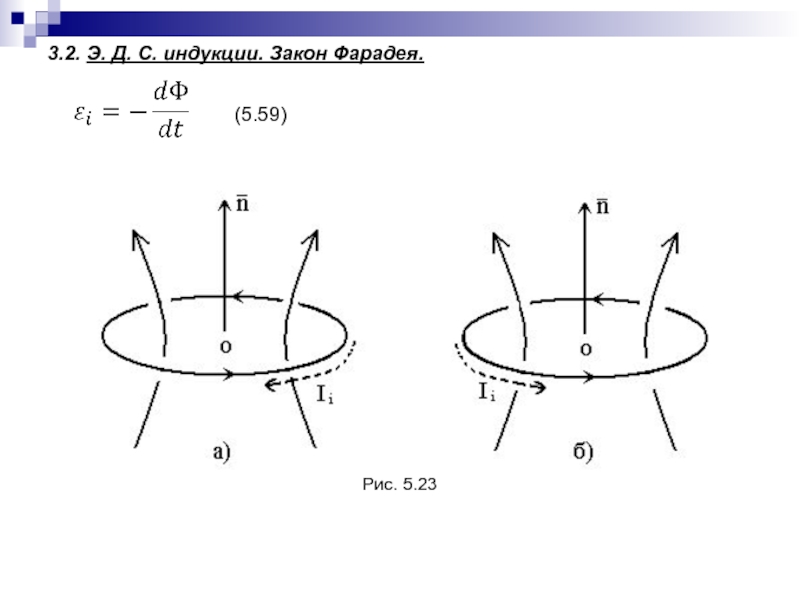
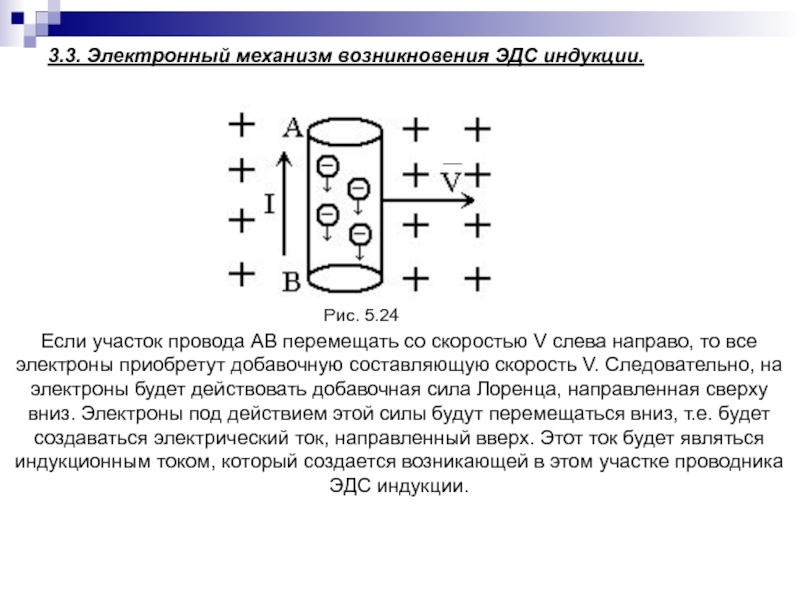
Слайд 123 3.3. Электронный механизм возникновения ЭДС индукции.
Если участок провода
АВ перемещать со скоростью V слева направо, то все электроны
приобретут добавочную составляющую скорость V. Следовательно, на электроны будет действовать добавочная сила Лоренца, направленная сверху вниз. Электроны под действием этой силы будут перемещаться вниз, т.е. будет создаваться электрический ток, направленный вверх. Этот ток будет являться индукционным током, который создается возникающей в этом участке проводника ЭДС индукции.Рис. 5.24
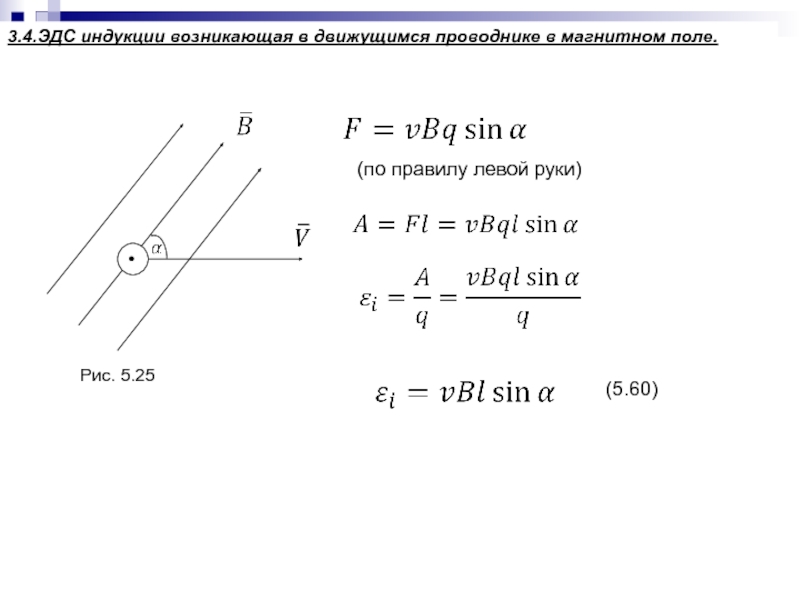
Слайд 124Рис. 5.25
(5.60)
3.4.ЭДС индукции возникающая в движущимся проводнике в магнитном поле.
(по
правилу левой руки)
Слайд 1273.7. Индуктивность соленоида.
Где n – число витков на единицу
длины соленоида;
I – ток в соленоиде;
N – полное число витков;l – длина соленоида.
(5.68)
(5.69)
Слайд 1283.8. Взаимная индукция.
(5.71)
Здесь L21 – коэффициент взаимной индукции контура
2 и контура 1.
Ф12 = L12I2
(5.72)где Ф12 – магнитный поток, создаваемый током I2 и пронизывающий контур I;
L12 – коэффициент взаимной индукции контура 1 и контура 2, и
(5.73)
Здесь Е1 – ЭДС индукции, возникающей в контуре I.
(5.74)
Рис. 5.27
Слайд 131Подставляя (5.80) в (5.78), имеем
или после интегрирования окончательно получаем
формулу энергии магнитного поля
(5.81)
Энергию магнитного поля через параметры, характеризующие это
поле (5.82)
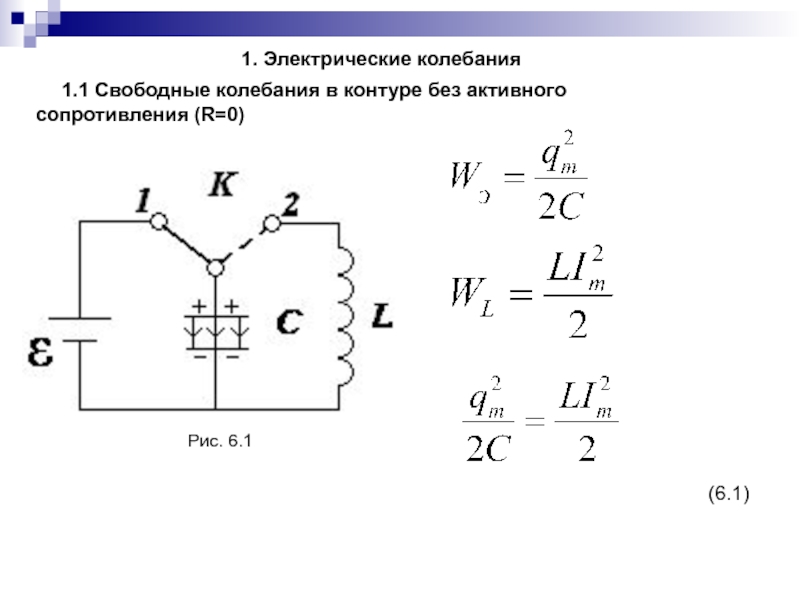
Слайд 1371.1 Свободные колебания в контуре без активного сопротивления (R=0)
(6.1)
Рис.
6.1
1. Электрические колебания
Слайд 139Для колебательного контура по 2-му правилу Кирхгофа:
(6.2)
, т.к.
, то
;
, тогда
;
(6.3)
(6.4)
(6.5)
(6.6)
(6.7)
Слайд 1483. Электромагнитные волны.
3.1. Плоская электромагнитная волна.
(6.43)
(6.45)
(6.44)
Рис. 6.7
Слайд 1521.2. Законы и квантовая теория фотоэффекта.
(7.1)
(7.2)
(7.3)
(7.4)
(7.5)
˜
Ф=const
Рис 7.4
V=const
Ф
Рис 7.5
Слайд 156С помощью тригонометрических уравнений:
Подставляем:
Вернемся к начальной системе
Подставим в выражение:
Слайд 1582. Элементы квантовой механики.
2.1. Корпускулярно-волновая двойственность свойств частиц вещества.
2.2.
Соотношения неопределенностей Гейзенберга.
(7.11)
(7.9)
(7.10)
(7.12)
(7.13)
(7.14)
(7.15)
Δ
Δ
Δ
Δ
Δ
Слайд 1593. Зонная теория твердых тел.
3.1. Энергетические уровни электронов.
Рис. 7.8
Рис. 7.8*
Рис.
7.9
(7.17)
(7.16)
(7.18)
Слайд 1613.3. Заполнение энергетических зон электронами.
Рис. 11
Рис. 7.12
(7.19)
При
Т=0. (рис. 7.12)
а) Если
Е.
б) Если Е>EF, то
.
При
а) Если Е=EF, то
.
Где Е - энергия данного уровня
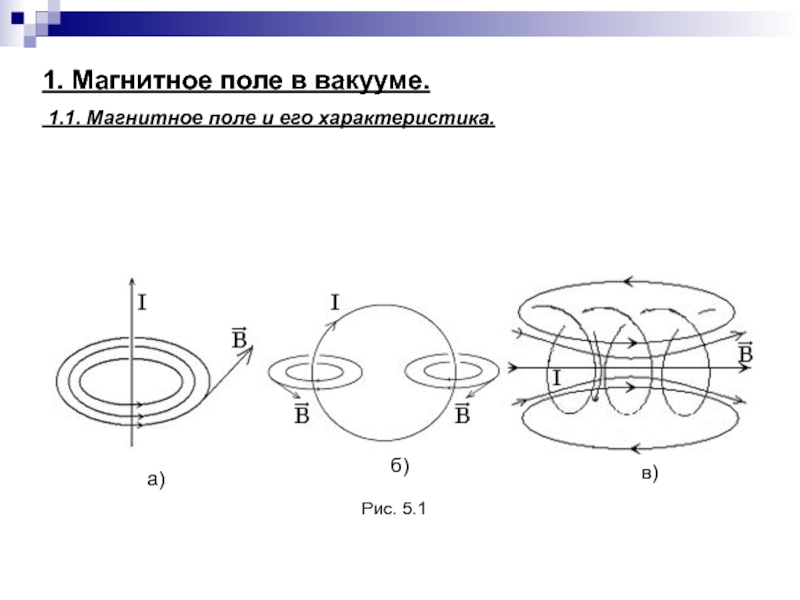
- уровень ферми
к – постоянная Больцмана
Т - температура
Слайд 166Рис 7.21
Рис 7.22
(7.20)
3.7 Вольтамперная характеристика p-n-перехода.
На рис 7.22 представлена вольтамперная
характеристика ВАХ p-n-перехода, она описывается уравнением (7.20)
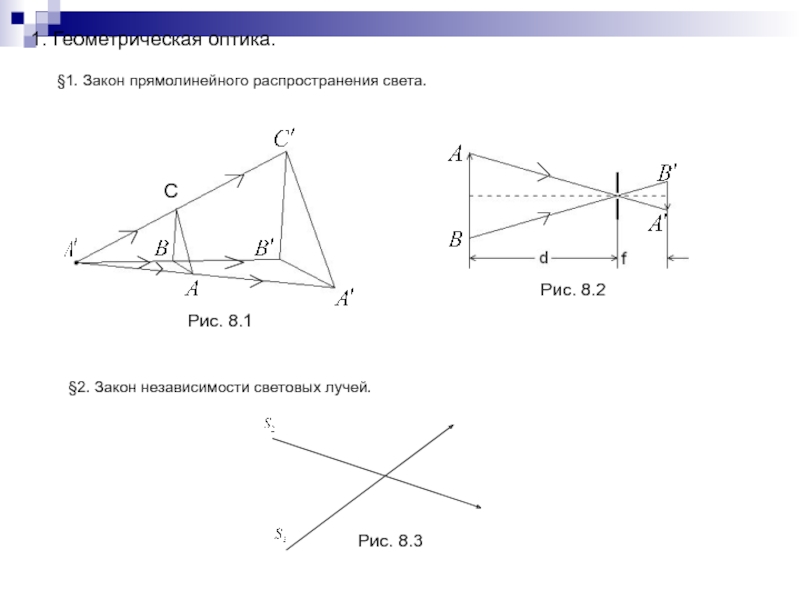
Слайд 1701. Геометрическая оптика.
§1. Закон прямолинейного распространения света.
§2. Закон независимости световых
лучей.
Рис. 8.1
Рис. 8.2
Рис. 8.3
С
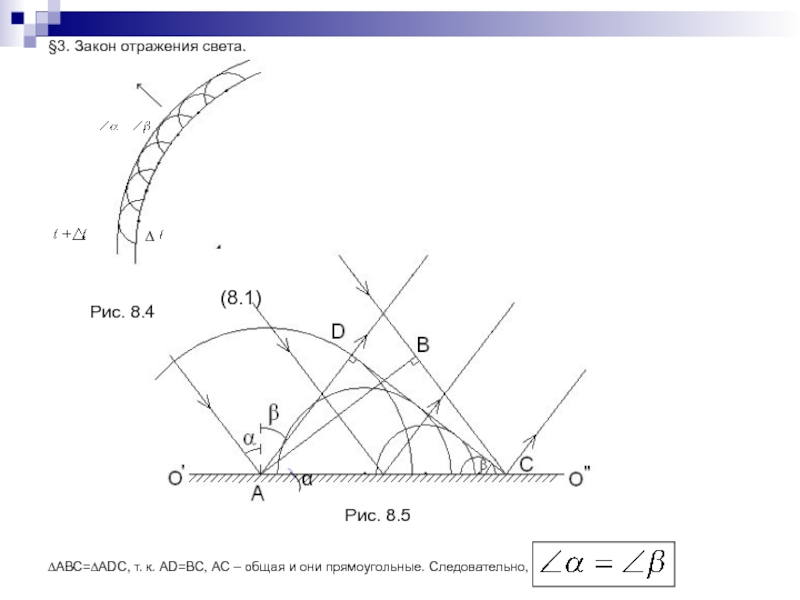
Слайд 171§3. Закон отражения света.
Рис. 8.5
Рис. 8.4
(8.1)
α
∆
∆АВС=∆ADC, т. к. AD=BC, АС
– общая и они прямоугольные. Следовательно,
.
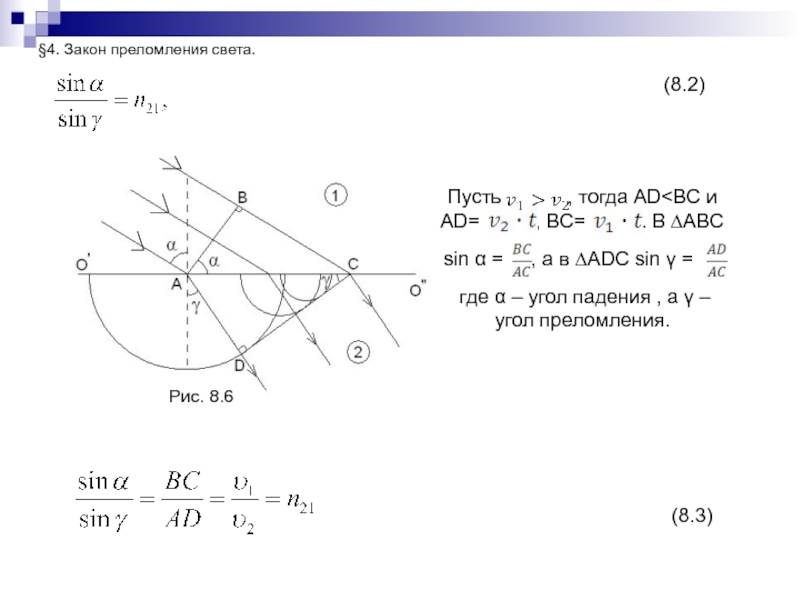
Слайд 172§4. Закон преломления света.
Рис. 8.6
(8.3)
(8.2)
Пусть
, тогда AD
BC= . B ∆ABCsin α = , а в ∆ADC sin γ = ,
где α – угол падения , а γ – угол преломления.
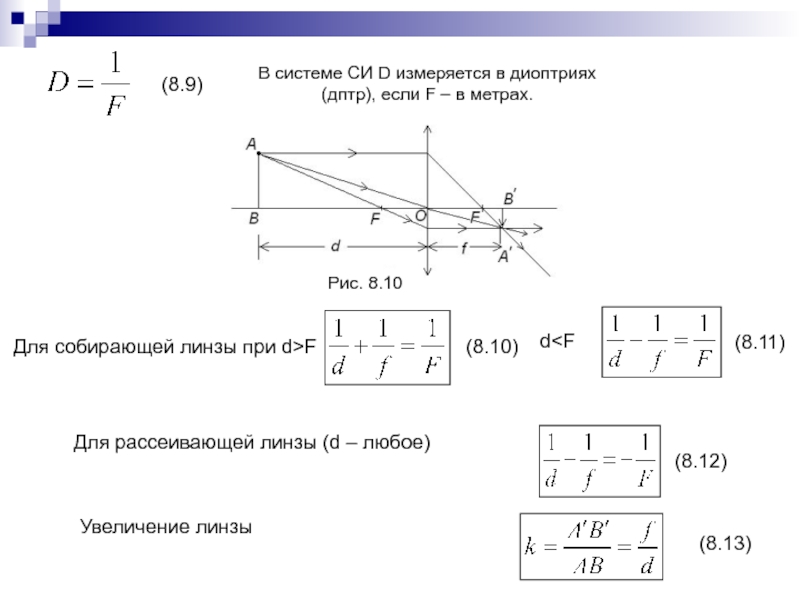
Слайд 175Рис. 8.10
(8.9)
(8.11)
(8.12)
(8.10)
(8.13)
В системе СИ D измеряется в диоптриях (дптр), если
F – в метрах.
Для собирающей линзы при d>F
d
(d – любое)Увеличение линзы
Слайд 1782. Интерференция света.
§1. Интерференция световых волн.
Рис. 8.13
(8.17)
(8.18)
(8.19)
(8.20)
(8.21)
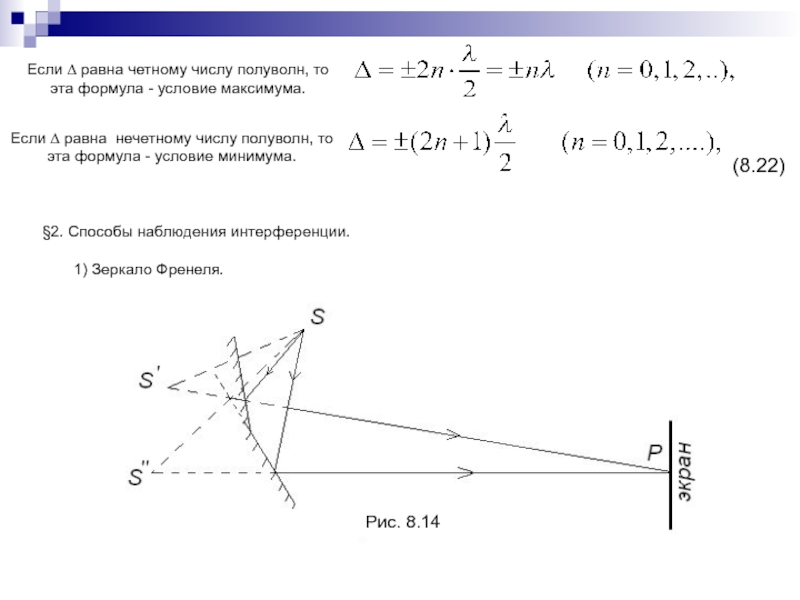
Слайд 179§2. Способы наблюдения интерференции.
1) Зеркало Френеля.
Рис. 8.14
(8.22)
Если ∆ равна четному числу
полуволн, то
эта формула - условие максимума.
Если ∆ равна нечетному числу
полуволн, тоэта формула - условие минимума.
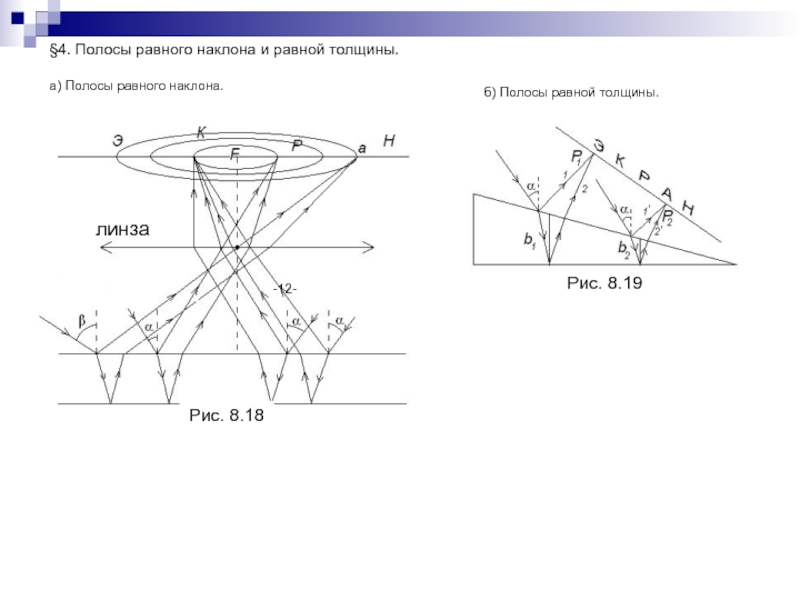
Слайд 182§4. Полосы равного наклона и равной толщины.
а) Полосы равного наклона.
-12-
б)
Полосы равной толщины.
Рис. 8.18
Рис. 8.19
линза
Слайд 186§3. Дифракция Френеля от простейших преград.
1) Дифракция от круглого отверстия.
-16-
Рис. 8.24
(8.39)
(8.40)
(8.41)
В
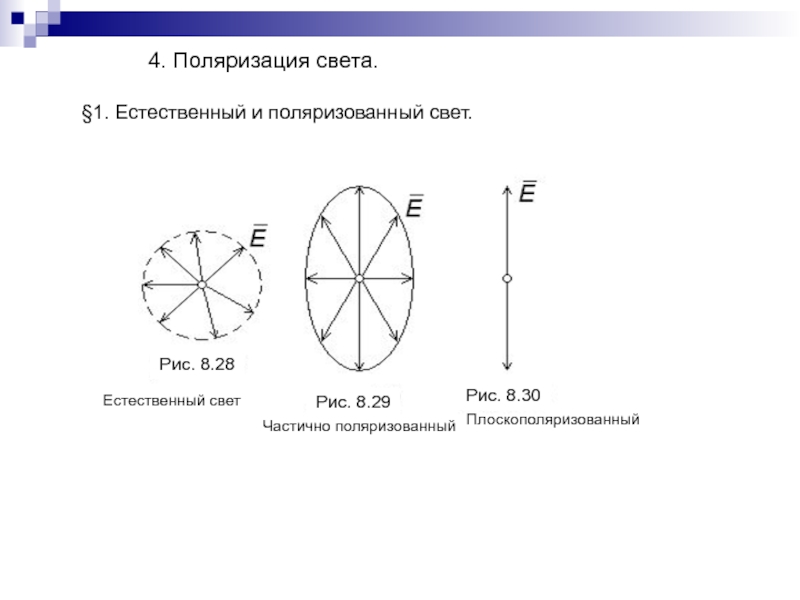
Слайд 1904. Поляризация света.
§1. Естественный и поляризованный свет.
Рис.
8.28
Рис. 8.29
Рис. 8.30
Естественный свет
Частично поляризованный
Плоскополяризованный
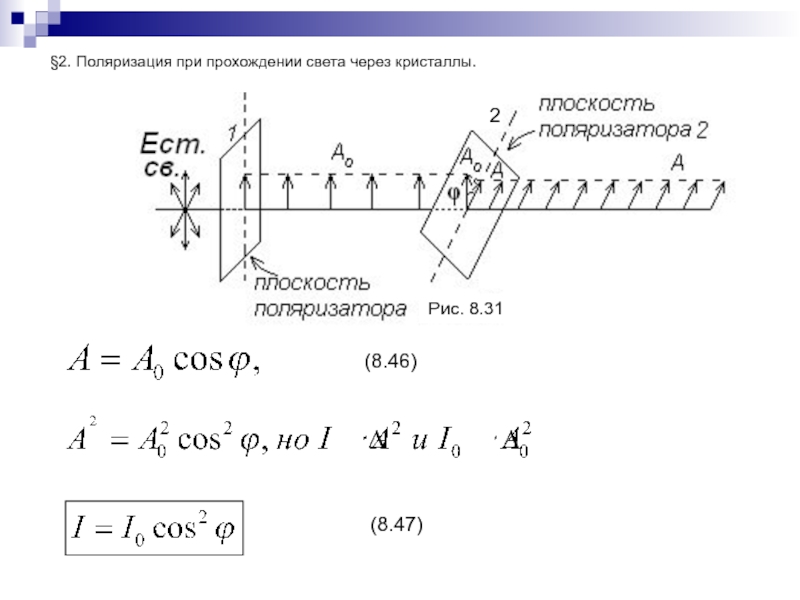
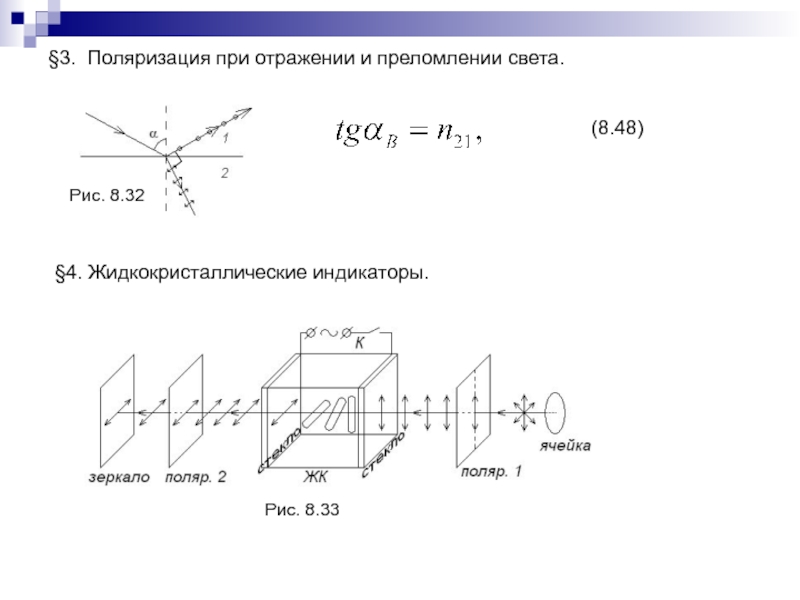
Слайд 192§3. Поляризация при отражении и преломлении света.
§4. Жидкокристаллические индикаторы.
Рис. 8.32
Рис. 8.33
(8.48)
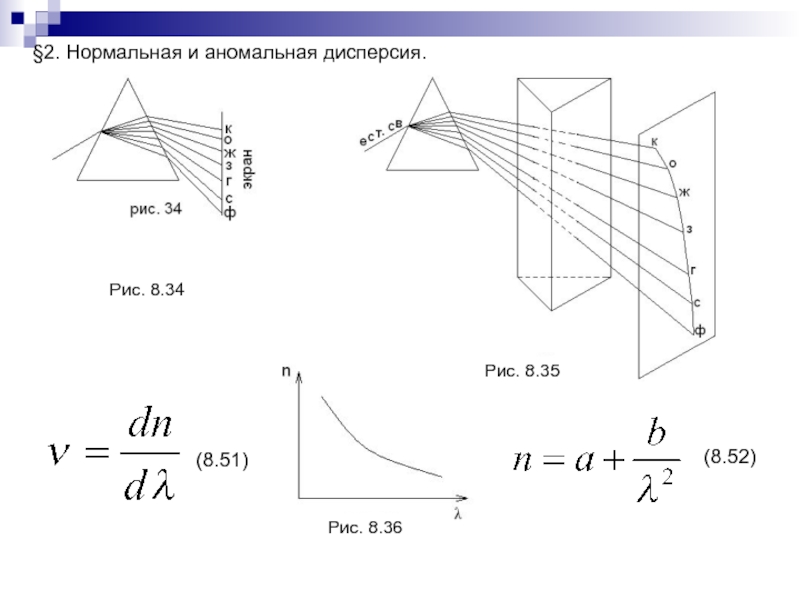
Слайд 198I. Атомная физика.
1. Боровская теория атома.
1.1. Закономерность в атомных спектрах.
(9.1)
серия
Пфунда
(9.2)
Слайд 2001.4. Постулаты Бора.
(9.3)
(9.4)
(9.5)
(9.6)
1.5 Элементарная боровская теория атома водорода
Из формулы (9.4)
Подставим
в (9.5)
Слайд 2032. Ядерная физика.
2.1. Состав и характеристика атомного ядра.
В свободном
состоянии нейтрон нестабилен.
Он спонтанно распадается, превращается в протон (р)
и испуская электрон (е-1) и антинейтрино ( ).(9.11)
N+Z=A (9.12)
Число нуклонов в ядре обозначается буквой А и называется массовым числом ядра
Символ обозначения ядер:
где Х – химический символ элемента.
Слайд 2042.2. Масса и энергия связи ядра.
(9.13)
Величина
называется дефектом массы
ядра.
2.3. Радиоактивность.
(9.15)
(9.16)
(9.17)
(9.18)
Слайд 205Имеется три вида радиоактивных излучений: α-лучи, β-лучи, γ-лучи.
α-распад протекает
по схеме:
α-лучи – поток ядер гелия
(9.19)
Пример:
β-лучи – поток
электронов. Он протекает по схеме:
(9.20)
Пример:
Слайд 2062.4. Ядерные реакции.
(9.21)
Примеры первых ядерных реакций:
2.5. Деление ядер.
Осколки претерпевают
превращения:
2.6. Термоядерные реакции.
s
s
Слайд 2073. Элементарные частицы
3.1. Классы и виды взаимодействий элементарных частиц
Известны четыре
вида взаимодействий между элементарными частицами:
- сильное
- электромагнитное
- слабое
- гравитационное
~
~
-2
-14
-39
2
-23
-21
-9
16
9
Слайд 208Элементарные частицы делятся на четыре класса.
1.Фотоны, (кванты электромагнитного
поля).
2. Лептоны : мюоны(
) , электроны( ) и нейтрино( ). 3. Адроны. Этот класс включает в себя сильно взаимодействующие частицы. Подразделяются на две подгруппы: мезоны и барионы.
Мезоны – сильно взаимодействующие нестабильные частицы. К их числу принадлежат - мезоны, К- мезоны и - мезоны.
4. Класс барионов объединяет в себе нуклоны (p, n) и нестабильные частицы с массой, большей массы нуклонов, получившие название гиперонов.