Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приемы и методы решения текстовых задач при подготовке к ОГЭ
Содержание
- 1. Приемы и методы решения текстовых задач при подготовке к ОГЭ
- 2. Одной из основных методических линий в курсе
- 3. Текст задачи – это рассказ о некоторых
- 4. Анализ текста задачи1) внимательное чтение задачи;2) первичный
- 5. Поиск способа решения задачи1) проведение вторичного (более
- 6. Оформление найденного способа решения задачи 1) оформление решения;2) запись результата решения задачи.
- 7. . Изучение найденного решения задачи1) контроль решения
- 8. Основные типы задач в ОГЭЗадачи на движение.
- 9. Задачи на проценты Решение задач на проценты
- 10. Памятка для решения задач на проценты Процентом
- 11. Задачи на «движение» Действие движения характеризуется тремя
- 12. Памятка при решении задач на движение Путь
- 13. Основными типами задач на движение являются следующие1)
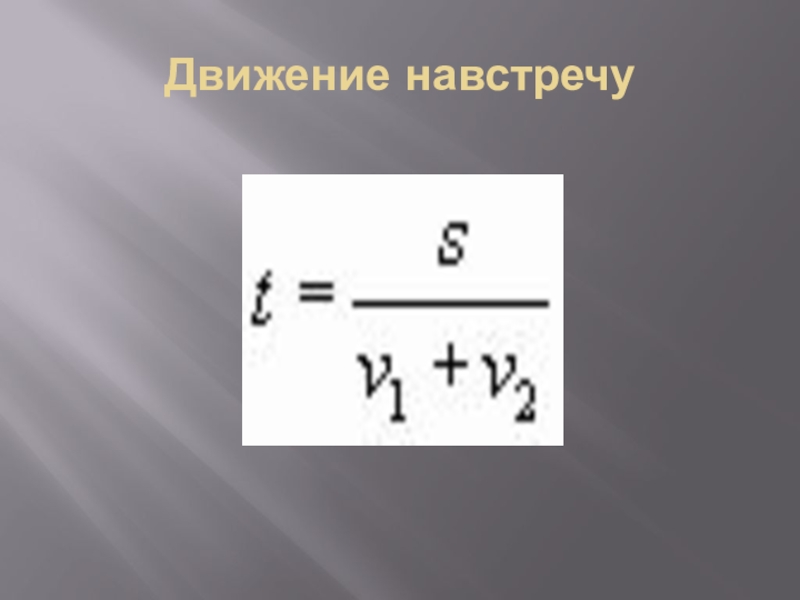
- 14. Движение навстречу
- 15. Расстояние между городами А и В
- 16. Движение вдогонку
- 17. Два пешехода отправляются из одного и того
- 18. Движение по окружности (замкнутой трассе)
- 19. Из одной точки круговой трассы, длина которой
- 20. Движение по воде От лесоповала вниз по
- 21. Решение: Пусть длина плота х км. Тогда
- 22. Средняя скорость
- 23. Путешественник переплыл море на яхте со средней
- 24. Движение протяжённых тел. Поезд, двигаясь равномерно со
- 25. Решение:65-5 =60 (км/ч)60 км/ч= м/сОтвет: 500.
- 26. Задачи на «концентрацию», на «смеси и сплавы»
- 27. Памятка для решения задач на концентрацию, смеси,
- 28. Задачи на процентное содержание влаги.При решении подобных
- 29. задачаСвежие фрукты содержат 72 % воды, а
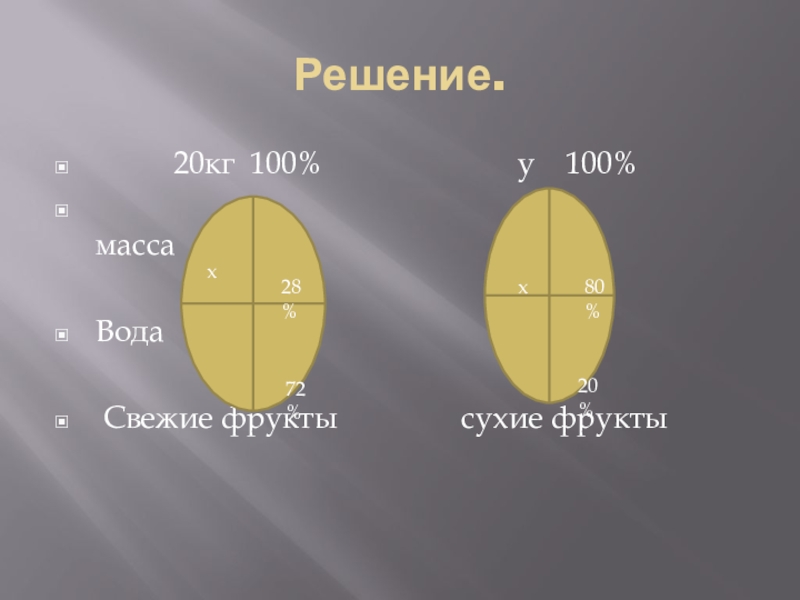
- 30. Решение. 20кг 100%
- 31. Из рисунка видим две пропорции.
- 32. Решение задач на растворы, смеси и сплавы
- 33. задачаИмеется два сплава меди и свинца. Один
- 34. схема
- 35. Старинный алгебраический метод или правило квадрата.Имеется лом
- 36. Слайд 36
- 37. Задачи «на работу» Работу характеризуют три компонента
- 38. Слайд 38
- 39. Два токаря вместе изготовили 350 деталей. Первый
- 40. Из А в В выехали одновременно два
- 41. Решение
- 42. Для выработки у учащихся внутренней потребности проверять
- 43. Способов проверки решения задачи много- Самый элементарный
- 44. Для проведения работы над задачей после ее
- 45. Спасибо за внимание
- 46. Скачать презентанцию
Одной из основных методических линий в курсе математики является линия обучения учащихся умению решать текстовые задачи. Известно, что решение текстовых задач представляет большие трудности для учащихся. Известно и то, какой именно
Слайды и текст этой презентации
Слайд 2Одной из основных методических линий в курсе математики является линия
обучения учащихся умению решать текстовые задачи.
Известно, что решение текстовых
задач представляет большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап – анализ текста задачи. Учащиеся плохо ориентируются в тексте задачи, в ее условиях и требовании
Слайд 3Текст задачи – это рассказ о некоторых жизненных фактах.
В тексте
важно все: и действующие лица, и их действия, и числовые
характеристики.При работе с математической моделью задачи (числовым выражением или уравнением) часть этих деталей опускается. Надо именно и научить умению абстрагироваться от некоторых свойств и использовать другие.
Слайд 4Анализ текста задачи
1) внимательное чтение задачи;
2) первичный анализ текста: выделение
вопроса задачи и ее условия;
3) оформление краткой записи текста задачи;
4)
выполнение чертежей, рисунков по тексту задачи.
Слайд 5Поиск способа решения задачи
1) проведение вторичного (более детального) анализа текста
задачи: выделение данных и искомых, установление связей между данными, между
данными и искомыми;2) выяснение полноты постановки задачи;
3) осуществление поиска решения, составление плана решения задачи;
4) перевод словесного текста задачи на математический язык;
5) привлечение теоретических знаний для решения задачи.
Слайд 6Оформление найденного способа решения задачи
1) оформление решения;
2) запись результата решения
задачи.
Слайд 7. Изучение найденного решения задачи
1) контроль решения задачи;
2) оценка результатов
решения;
3) анализ способов решения и их обобщение;
4) составление новых задач.
Слайд 8Основные типы задач в ОГЭ
Задачи на движение.
Задачи на работу.
Задачи на смеси и сплавы.
Задачи на проценты.
Задачи на
прогрессии.
Слайд 9Задачи на проценты
Решение задач на проценты сводится к основным
трем действиям с процентами:
нахождение процентов от числа;
нахождение числа
по его процентам; нахождение процентного отношения чисел.
Слайд 10Памятка для решения задач на проценты
Процентом числа называется его
сотая часть.
Например:
1% от числа 500 – это число
5.-нахождение процента от числа:
Найти 3 % от числа 500;15 % от числа 60. -нахождение числа по его процентам:
Найти число, 12% которого равны 30.
-нахождение % отношения чисел:
Сколько % составляет 120 от 600?
Слайд 11Задачи на «движение»
Действие движения характеризуется тремя компонентами: пройденный путь,
скорость и время.
Известно соотношение между ними:
Путь = скорость
• время
Слайд 12Памятка при решении задач на движение
Путь = скорость ·
время
При движении по реке:
Скорость по течению = собственная
скорость транспорта + скорость течения рекиСкорость против течения = собственная скорость транспорта - скорость течения реки
Слайд 13Основными типами задач на движение являются следующие
1) задачи на движение
по прямой (навстречу и вдогонку);
2) задачи на движение по замкнутой
трассе;3) задачи на движение по воде;
4) задачи на среднюю скорость;
5) задачи на движение протяжённых тел.
Слайд 15 Расстояние между городами А и В равно 580 км.
Из города А в город В со скоростью 80 км/ч
выехал автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Через сколько часов после выезда второго автомобиля автомобили встретятся?Решение:
1) 80*2=160(км) – проехал первый автомобиль
2) (580-160)/(80+60)=3(ч)
Ответ: 3
Слайд 17Два пешехода отправляются из одного и того же места в
одном направлении на прогулку по аллее парка. Скорость первого на
1 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 200 метрам?Решение:
200м = 0,2 км.; ; 0, 2 часа=12 минут
Ответ: 12.
Слайд 19Из одной точки круговой трассы, длина которой равна 10 км/ч,
одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля
равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.Решение:
Пусть скорость второго автомобиля х км/ч. Так как 40 минут = часа и это время, за которое первый автомобиль будет опережать второй на один круг, составим уравнение
; 30 = 180 – 2х; 2х = 150; х = 75
Ответ: 75.
Слайд 20Движение по воде
От лесоповала вниз по течению реки движется со
скоростью 3 км/ч плот. Плотовщик доплывает на моторке из конца
плота к его началу и обратно за 16 минут 40 секунд. Найдите длину плота, если собственная скорость моторки равна 15 км/ч. Ответ дайте в километрах
Слайд 21Решение:
Пусть длина плота х км. Тогда скорость моторки по течению
18 км/ч, а против течения 12 км/ч. Так как 16
минут 40 секунд = часа, то;
2х + 3х = 10;
5х = 10;
х = 2.
Ответ: 2
Слайд 23Путешественник переплыл море на яхте со средней скоростью 20 км/ч.
Обратно он летел на спортивном самолёте со скоростью 480 км/ч.
Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.Решение:
25t=960; t= 38,4
Ответ: 38,4.
Слайд 24Движение протяжённых тел.
Поезд, двигаясь равномерно со скоростью 65 км/ч,
проезжает мимо идущего в том же направлении параллельно путям со
скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
Слайд 26Задачи на «концентрацию», на «смеси и сплавы»
В задачах этого
типа обычно присутствуют три величины, соотношение между которыми позволяет составлять
уравнение:Концентрация (доля чистого вещества в смеси);
Количество чистого вещества в смеси (или сплаве);
Масса смеси (сплава).
Соотношение между этими величинами следующее:
Масса смеси • концентрация = количество чистого вещества
Слайд 27Памятка для решения задач на концентрацию, смеси, сплавы
концентрация(доля чистого вещества
в смеси)
-количество чистого вещества в смеси
-масса смеси.
масса
смеси · концентрация = количество чистого вещества.
Слайд 28Задачи на процентное содержание влаги.
При решении подобных задач следует определить
ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной
в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. В рассматриваемых задачах эту величину будем обозначать х.
Слайд 29задача
Свежие фрукты содержат 72 % воды, а сухие – 20
% воды. Сколько сухих фруктов получится из 20 кг свежих?
Слайд 32Решение задач на растворы, смеси и сплавы с помощью схемы.
Схему оформляют в виде прямоугольников, разделённых пополам.
Слайд 33задача
Имеется два сплава меди и свинца. Один сплав содержит 15%
меди, а другой 65% меди. Сколько нужно взять каждого сплава,
чтобы получилось 200г сплава, содержащего 30% меди?
Слайд 35Старинный алгебраический метод или правило квадрата.
Имеется лом стали двух сортов
с содержанием никеля 5% и 40%. Сколько нужно взять металла
каждого из этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?
Слайд 37Задачи «на работу»
Работу характеризуют три компонента действия:
Время работы,
Объем работы,
Производительность (количество произведенной работы в единицу времени). Существует
следующее соотношение между этими компонентами:Объем работы = время работы • производительность
Слайд 39Два токаря вместе изготовили 350 деталей. Первый токарь делал в
день 40 деталей и работал 5 дней, второй работал на
2 дня меньше. Сколько деталей в день делал второй токарь?
Слайд 40Из А в В выехали одновременно два автомобиля. Первый проехал
весь путь с постоянной скоростью. Второй проехал первую половину пути
со скоростью, меньшей скорости первого на 14 км/ч, а вторую половину пути – со скоростью 105 км/ч. Прибыли в В одновременно. Скорость первого - ? Если известно, что она больше 50 км/ч. Ответ в км/ч.
Слайд 42Для выработки у учащихся внутренней потребности проверять решение задачи необходимо
научить их:
1. При решении задачи обязательно объясните себе, почему решаете
так, а не иначе.2. После решения задачи прочитайте снова текст задачи и проверьте, все ли требования задачи выполнены, правильно ли.
3. Составьте план решения задачи. Какой пункт в решении задачи будет последним? (Работа над задачей заканчивается проверкой ее решения).
Слайд 43Способов проверки решения задачи много
- Самый элементарный – прикидка ответа
(установление границ искомого числа). Прикидка позволяет заметить неправильность рассуждения, несоответствие
между величинами, но для многих задач не применим.- Самый полезный, универсальный – составление и решение обратной задачи. Этот способ проверки развивает мышление, рассуждение, но громоздкий и отнимает много времени.
- Самый надежный способ проверки – решение задачи другим способом.
Слайд 44Для проведения работы над задачей после ее решения используют следующие
приемы: преобразование задачи, сравнение задач, самостоятельное составление аналогичных задач, обсуждение
разных способов решения задачи.
