Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прийняття рішень в умовах визначеності
Содержание
- 1. Прийняття рішень в умовах визначеності
- 2. Лекція 2. Прийняття рішень при багатьох критеріяхЗміст
- 3. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 Проблема багатокритеріальності. Змістовний аналіз
- 4. Суть багатокритеріальних задач прийняття рішень.Змістовний аналіз
- 5. Суть багатокритеріальних задач прийняття рішень.Змістовний аналіз
- 6. Суть багатокритеріальних задач прийняття рішень.Відношення Парето,
- 7. Вільфре́до Паре́то (італ. Vilfredo Pareto; *15
- 8. Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/14
- 9. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоПрипустимо,
- 10. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоВідношення
- 11. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоВідношення
- 12. Суть багатокритеріальних задач прийняття рішеньЩоб вибрати
- 13. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоЩоб вибрати
- 14. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоПарето-оптимальні
- 15. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоМайте
- 16. Відношення Парето, Парето-оптимальні рішення, безліч Парето
- 17. Відношення Парето, Парето-оптимальні рішення, безліч ПаретоКажуть,
- 18. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/202. Формальна Постановка Задачі багатокритеріальної оптимізації
- 19. /22Приклад задачі Товариство, утворене трьома засновниками,
- 20. /22 x1+x2+x3 ≤ b1 –баланс земельних угідь,гаa12x1+a22x2+a32x3
- 21. /22Задача векторного програмування Це задача знаходження
- 22. /22Задача векторного програмуванняРішення задачі векторного програмування часто
- 23. /22Задача векторного програмування в загальному виглядіЗадача математичного
- 24. /22Лінійна Задача векторного програмування в загальному виглядіЗадача
- 25. /22Задача векторного програмування в загальному вигляді Теорія Прийняття рішень © ЄА. Лавров, 2014-2019
- 26. 3.Проблеми та класифікація методів вирішення задач багатокритеріальної оптимізаціїТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 27. Проблеми та класифікація методів вирішення задач багатокритеріальної оптимізації Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 28. Проблеми та класифікація методів вирішення задач багатокритеріальної
- 29. Нормалізація (нормування) критеріївПри вирішенні багатокритеріальної задачі часто
- 30. Методи вирішення задач багатокритеріальної оптимізації.Розвиваються за трьома
- 31. /22Класифікація методів вирішення задач багатокритеріальної оптимізації Теорія Прийняття рішень © ЄА. Лавров, 2014-2019
- 32. Класифікація методів вирішення задач багатокритеріальної оптимізації. Методи,
- 33. Методи, основані на згортанні критеріїв. Адитивнана згорткаНехай
- 34. Методи, основані на згортанні критеріїв. Мультиплікативна згортка
- 35. /22 Недолік методів згортання критеріїв
- 36. /22 Метод головного критерія Вибирається основний
- 37. /22 Метод головного критерія Теорія Прийняття
- 38. /22 Метод послідовних поступок В
- 39. /22 Метод послідовних поступок В
- 40. /22 Метод послідовних поступок 2-й
- 41. /22 Метод послідовних поступок 3-й крок. Призначається
- 42. /22 Метод послідовних поступок K-й крок.
- 43. /22 Метод послідовних поступок. Основний Недолік
- 44. /22 Метод цільового програмування Назва цієї
- 45. /46 Метод цільового програмування Задачу можна
- 46. /46 Метод цільового програмування Ускладнення, зумовлені
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Лекція 2. Прийняття рішень при багатьох критеріях
Зміст лекції:
Проблема багатокритеріальності Змістовний
аналіз
Формальна Постановка Задачі багатокритеріальної оптимізації
Проблеми та класифікація методів вирішення задач
багатокритеріальної оптимізаціїТеорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 3Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Проблема багатокритеріальності. Змістовний
аналіз
Слайд 4 Суть багатокритеріальних задач прийняття рішень.Змістовний аналіз
До цих пір ми
розглядали задачі оптимізації, де 1 критерій (показник ефективності) за яким
проводиться оцінка ефективності об'єкта, тобто потрібно звернути в min (max) один єдиний показник.Такі завдання на практиці зустрічаються рідко. Коли йде мова про проектування таких об'єктів як літак, технологічний процес, то їх ефективність, як правило, не може бути повністю оцінена за допомогою єдиного показника.
Доводиться розглядати додаткові критерії (показники ефективності). Чим більше критеріїв якості вводиться в розгляд, тим більш повну характеристику достоїнств і недоліків проектованого об'єкта можна отримати.
Таким чином, завдання проектування складних систем завжди багатокритеріальні, тому що при виборі найкращого варіанту доводиться враховувати багато різних вимог, пред'явлених до системи (об'єкту).
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 5 Суть багатокритеріальних задач прийняття рішень.Змістовний аналіз
Варіанти-"кандидати" порівнюються за двома
або більше критеріями, щоб знайти оптимальний варіант
(або один з
оптимальних, якщо "перше місце" ділять різні "кандидати").Приклад: вибираємо, який вид танка вибрати на озброєння військ, критерії - захищеність, зручність екіпажу, ефективність озброєння, швидкість.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 6 Суть багатокритеріальних задач прийняття рішень.Відношення Парето, Парето-оптимальні рішення, безліч
Парето
? ЯК простим способом скоротити число варіантів, особливо якщо
таких багато. Нехай, наприклад, ми вибираємо стратегію розвитку підприємства критерії –очікуваний прибуток на рік (в сенсі мат. очікування з теорії ймовірностей),
надійність стратегії (ймовірність того, що буде прийнятний для нас прибуток, хоч скільки-небудь солідний дохід).
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 7Вільфре́до Паре́то
(італ. Vilfredo Pareto; *15 липня; *15 липня 1848;
*15 липня 1848, Франція; *15 липня 1848, Франція—† 19 серпня;
*15 липня 1848, Франція—† 19 серпня 1923; *15 липня 1848, Франція—† 19 серпня 1923, Лозанна; *15 липня 1848, Франція—† 19 серпня 1923, Лозанна, Швейцарія) — італійський економіст і соціолог, зробив важливий внесок в економіку, соціологію і моральну філософію. Він ввів поняття ефективності Парето і допоміг розвитку галузі мікроекономіки. Його теорії вплинули на Беніто Муссоліні. Його теорії вплинули на Беніто Муссоліні і розвиток Італійського фашизму.Сім'я Парето переселилась у Італію в 1858 році. У 1870 отримав ступінь інженера у Туринському Політехнічному Інституті і отримав роботу у італійськії залізниці. У 1886 читав лекції по економіці та менеджменту у Флорентійському Університеті. У 1893 був призначений лектором в Університеті Лозанни у Швейцарії де і залишився до кінця життя.
В 1906 році, він зробив добре відоме спостереження, що 20 % населення володіють 80 % власності у Італії, пізніше узагальнене (Джозефом М. Юраном та іншими) у так званий принцип Парето (для багатьох явищ 80 % наслідків спричинені 20 % причин), ще пізніше узагальнене у понятті розподілу Парето.
Індекс Парето — це міра нерівномірності розподілу доходу.
Діаграма ПаретоДіаграма Парето — це спеціальний тип гістограмиДіаграма Парето — це спеціальний тип гістограми, яка використовується щоб розглядати причини подій в порядку спадання від найбільшої до найменшої. Це статистичний інструмент, що графічно інтерпретує правило 80-20.
Парето написав роботу про соціальну політику «Розум і суспільство».
Заснував теорію еліт.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 9 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Припустимо, у нас є
5 стратегій:
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Стратегія 2 дає
більше прибутку, ніж стратегія 1, при тій же надійності. стратегія 1 не може бути кращою. Стратегія 3 по очікуваного прибутку рівноцінна стратегії 2, але надійніше. стратегія 2 теж невигідна.
Стратегія 3 прибутковіше стратегії 4 при тій же надійності.
стратегія 4 теж невиправдана
Залишаються лише стратегії 3 і 5. За одним критерієм перевершує одна, по іншому - інша. Ми не змогли прийти до 1-го варіанту, але усунули більшість завідомо негідних.
Слайд 10 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Відношення Парето.
Варіант x
краще варіанта y по відношенню Парето
(далі: x> y), якщо
x хоча б за одним критерієм краще, ніж y,
а по решті критеріїв x не гірше, ніж y.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 11 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Відношення Парето.
Варіант x
краще варіанту y по відношенню Парето (далі: x> y), якщо
x хоча б за одним критерієм краще, ніж y, а по решті критеріїв не гірше, ніж y.Дане відношення транзитивно (якщо x> y і y> z, то x> z), антерефлексівно (неможливо x> x), асиметрично (неможливо одночасно x> y і y> x), тобто це відношення строгого порядку.
Зауважимо, що між конкретною парою (x, y) не завжди можна встановити відношення Парето, як це було у випадку стратегій 3 і 5 в нашому прикладі.
Таке ставлення не встановлюється, якщо кожен з пари в чомусь краще, а в чомусь гірше "партнера "
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 12 Суть багатокритеріальних задач прийняття рішень
Щоб вибрати конкретне рішення з
Парето-оптимальної безлічі
(якщо в ньому більше одного варіанту),
потрібні якісь
додаткові дані, наприклад, відомості про пріоритети критеріїв.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 13Відношення Парето, Парето-оптимальні рішення, безліч Парето
Щоб вибрати конкретне рішення з
Парето-оптимального безлічі (якщо в ньому більше одного варіанту), потрібні якісь
додаткові дані, наприклад, відомості про пріоритети критеріїв.Припустимо, у Васі вибір - з якою дівчиною зустрічатися:
Катя красива, але не дуже розумна,
Маша розумна, але не дуже красива шна,
Дуся і не розумна, і некрасива
Васі потрібна дівчина розумніше і красивіше.
Парето-оптимальна безліч: {Катя, Маша}. Далі Парето не помічник, тут вже що важливіше - розум чи краса?
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
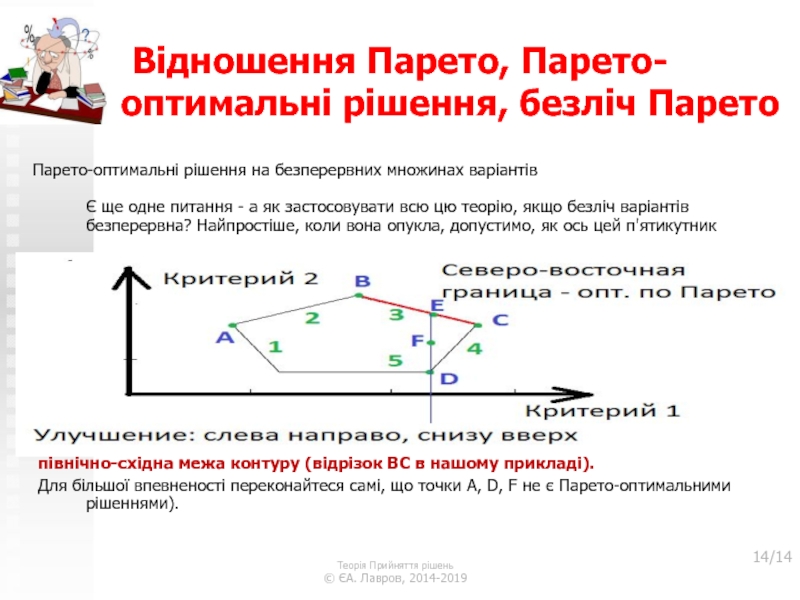
Слайд 14 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Парето-оптимальні рішення на безперервних
множинах варіантів Є ще одне питання - а як застосовувати
всю цю теорію, якщо безліч варіантів безперервна? Найпростіше, коли вона опукла, допустимо, як ось цей п'ятикутникНеважко переконатися, що Парето-оптимальна безліч –
північно-східна межа контуру (відрізок BC в нашому прикладі).
Для більшої впевненості переконайтеся самі, що точки A, D, F не є Парето-оптимальними рішеннями).
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 15 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Майте на увазі: це
правило вірно, якщо нам потрібно, щоб величини критерії були якомога
більше. Останнє не завжди буває так. Наприклад, вартість придбання, витрата палива повинні зводитися до мінімуму.В цьому випадку потрібно замінити "мін" на "макс" аналоги,
наприклад, витрата - на економію,
ймовірність збою - на ймовірність безперебійного функціонування ...
Скажімо, якщо ймовірність збою = 0,02, то надійність становить 0,98.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 16 Відношення Парето, Парето-оптимальні рішення, безліч Парето
якщо безліч неопукла
Зрозуміло, що
знову поза північно-східного кордону не може бути Парето-оптимальних варіантів. Отже,
Парето-оптимальні варіанти можуть бути тільки на ламаній ABCD, але й тут є "негідні" варіанти.Залишається їх відсіяти.
Провівши побудови, як на малюнку, бачимо, що безліч Парето утворюється з двох груп варіантів.
Відрізок AE, виключаючи точку E (оскільки C> E), за рахунок високих показників по другому критерію.
Відрізок CD - за рахунок високих показників за першим критерієм.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 17 Відношення Парето, Парето-оптимальні рішення, безліч Парето
Кажуть, що ресурси розподілені
оптимально по Парето, коли ніхто не може поліпшити становище без
того, щоб в результаті для кого-небудь воно не погіршилося.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 18Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
2. Формальна Постановка Задачі
багатокритеріальної оптимізації
Слайд 19/22
Приклад задачі
Товариство, утворене трьома засновниками, має на меті максимізацію
прибутку кожного із засновників.
Перший засновник за свій рахунок орендує
для товариства землю (b1), а привласнює тільки виручку від реалізації зерна. Другий купує за свій рахунок добрива (b2), а привласнює тільки виручку від реалізації картоплі.
Третій отримує і оплачує кредит (b3), присвоює виручку від реалізації капусти.
Відомі потреби культур в добривах і в оборотному капіталі (A), ціни культур (c) і ресурсів (d).
Площі під названими культурами - x1, x2 і x3 відповідно.
Знайти план, при якому кожен з учасників товариства отримує максимальний прибуток
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 20/22
x1+x2+x3 ≤ b1 –баланс земельних угідь,га
a12x1+a22x2+a32x3 ≤ b2 –
баланс добрив, т
a13x1+a23x2+a33x3 ≤ b3 – баланс оборотного капіталу, тис
грн. max c1x1 – d1b1 – прибуток першого засновника, тис. грн.
max c2x2 – d2b2 – прибуток друго засновника, тис. грн.
max c3 x3 – d3b3 - прибуток третього засновника, тис. грн.
При таких обставинах майже завжди існує безліч рішень, при яких кожна цільова функція виявляється в оптимумі.
Але ці рішення не рівноцінні з позицій кожного з учасників товариства.
Один з них вважатиме за краще одне рішення, інший - інше.
Не існує формального правила вирішення цього конфлікту,
якщо тільки учасники самі не домовляться про яке-небудь правило
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Приклад задачі
Слайд 21/22
Задача векторного програмування
Це задача знаходження оптимуму
двох або більше
функцій,
що задовольняє умовам, заданим у формі рівнянь і нерівностей.
Рішенням задачі векторного програмування вважається
вектор таких значень її змінних,
при яких не можна поліпшити
значення жодної цільової функції інакше,
ніж за рахунок погіршення іншої цільової функції.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 22/22
Задача векторного програмування
Рішення задачі векторного програмування
часто називають оптимумом по
Парето (На честь видатного італійського економіста XIX століття, який вперше
сформулював таку задачу запропонував принцип непогіршення цільових функцій).Всю сукупність різних оптимумів по Парето задачі векторного програмування часто називають
МножиноюПарето або поверхнею Парето
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 23/22
Задача векторного програмування в загальному вигляді
Задача математичного програмування:
max z(x)
f(x) ≤
b
x ≥ 0
Задача векторного програмування:
max z(x)
f(x) ≤ b
x ≥ 0
Скаляр
Вектор
Теорія
Прийняття рішень © ЄА. Лавров, 2014-2019
Слайд 24/22
Лінійна Задача векторного програмування в загальному вигляді
Задача лінійного програмування:
max cx
Ax
≤ b
x ≥ 0
Лінійна задача векторного програмування:
max Cx
Ax ≤ b
x
≥ 0Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 25/22
Задача векторного програмування в загальному вигляді
Теорія Прийняття рішень
©
ЄА. Лавров, 2014-2019
Слайд 26
3.Проблеми та класифікація методів вирішення задач багатокритеріальної оптимізації
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 27Проблеми та класифікація методів вирішення задач багатокритеріальної оптимізації
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 28Проблеми та класифікація методів вирішення задач багатокритеріальної оптимізації
При вирішенні задач
БКО доводиться вирішувати специфічні питання, пов'язані з невизначеністю цілей і
несумірністю критеріїв.основні проблеми, що виникають при розробці методів МКО. 1. Проблема нормалізації критеріїв, тобто приведення критеріїв до єдиного (безрозмірного) масштабом виміру. 2. Проблема вибору принципу оптимальності, тобто встановлення, в якому сенсі оптимальне рішення краще за всіх інших рішень. 3. Проблема врахування пріоритетів критеріїв, що виникає в тих випадках, коли з фізичного змісту ясно, що деякі критерії мають пріоритет над іншими. 4. Проблема обчислення оптимуму задачі МКО. Йдеться про те, як використовувати методи лінійної, нелінійної, дискретної оптимізації для обчислення оптимуму задач з певною специфікою
Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Слайд 29Нормалізація (нормування) критеріїв
При вирішенні багатокритеріальної задачі часто виникає необхідність нормалізації
(нормування) критеріїв
тобто приведення всіх критеріїв до єдиного масштабу і
безрозмірного вигляду. Надалі будемо вважати, що всі критерії невід'ємні, тобто для всіх .
Найбільш часто використовується заміна критеріїв їх безрозмірними відносними величинами: , де Нормалізовані критерії мають двома важливими властивостями: по-перше, вони є безрозмірними величинами, і, по-друге, вони задовольняють нерівності для будь-якого .
Ці властивості дозволяють порівнювати критерії між собою.
Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
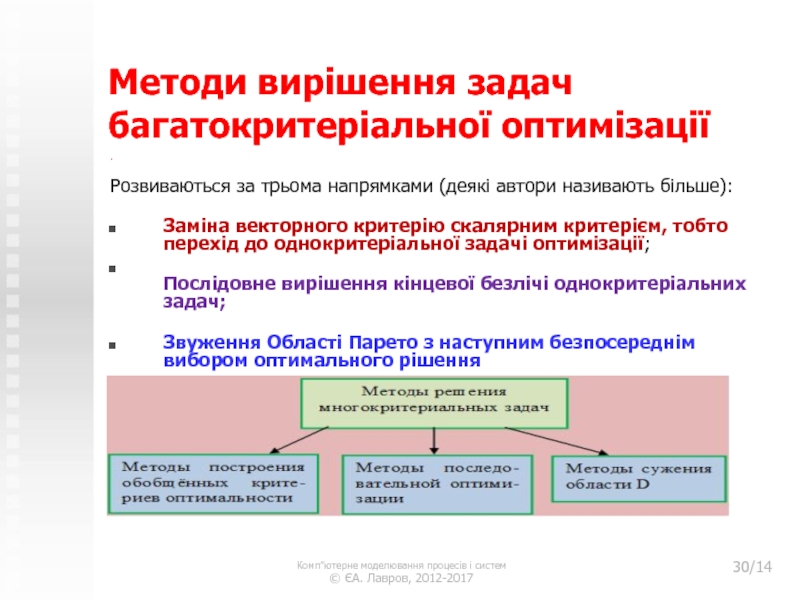
Слайд 30Методи вирішення задач багатокритеріальної оптимізації
.
Розвиваються за трьома напрямками (деякі автори
називають більше):
Заміна векторного критерію скалярним критерієм, тобто перехід до
однокритеріальної задачі оптимізації; Послідовне вирішення кінцевої безлічі однокритеріальних задач;
Звуження Області Парето з наступним безпосереднім вибором оптимального рішення
Комп”ютерне моделювання процесів і систем
© ЄА. Лавров, 2012-2017
/14
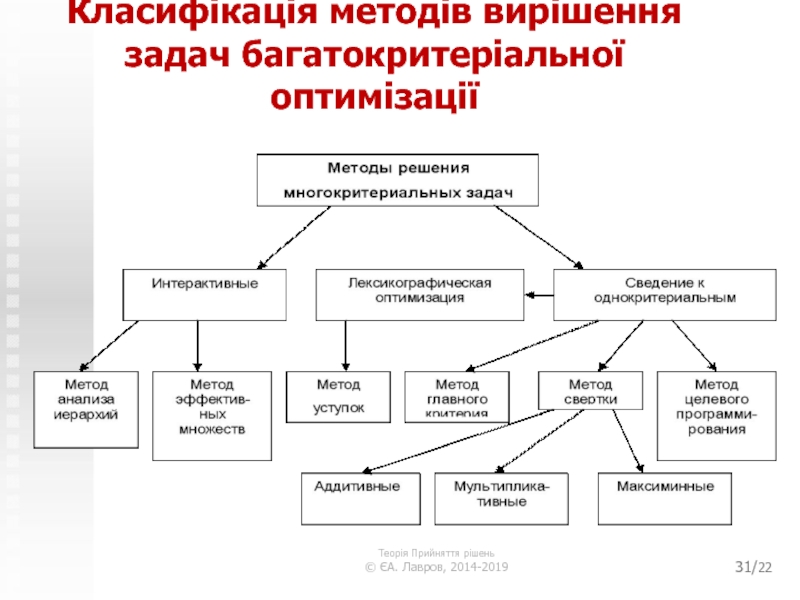
Слайд 31/22
Класифікація методів вирішення задач багатокритеріальної оптимізації
Теорія Прийняття рішень
©
ЄА. Лавров, 2014-2019
Слайд 32Класифікація методів вирішення задач багатокритеріальної оптимізації. Методи, основані на згортанні
критеріїв
Замість часткових критеріїв
розглядається один скалярний критерій,
отриманий шляхом комбінації часткових критеріїв. Розрізняють
адитивний і
мультиплікативний
методи згортання критеріїв.
Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Слайд 33Методи, основані на згортанні критеріїв. Адитивнана згортка
Нехай критерії співмірні, наприклад,
нормовані та визначено вектор вагових коефіцієнтів критеріїв
, що характеризують важливість відповідного критерію.Це значить, що , якщо критерій має пріоритет над критерієм . при цьому
Для адитивного методу будується нова цільова функція
і вирішується задача оптимізації скалярного критерію за умови
Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Слайд 34Методи, основані на згортанні критеріїв. Мультиплікативна згортка
Для мультиплікативного методу підхід
до вирішення аналогічний, тільки цільова функція має вигляд
Причому.
Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Слайд 35/22
Недолік методів згортання критеріїв
Основний і дуже суттєвий
Недолік
суб'єктивність вибору коефіцієнтів
!!!!!!!!!!!!!!
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 36/22
Метод головного критерія
Вибирається основний (головний) серед критеріїв. Нехай це,
наприклад
.Всі інші цільові функції переводяться в розряд обмежень:
Відповідно до вимог ОПР на всі критерії накладаються певні обмеження, яким вони повинні задовольняти. Вводиться система контрольних показників , щодо яких за всіма критеріями мають бути досягнуті значення, що не менше заданих значень
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 37/22
Метод головного критерія
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Після
вибору основного критерію і встановлення нижніх меж для решти критеріїв
вирішується задача однокритеріальної оптимізації::при умовах
Слайд 38/22
Метод послідовних поступок
В цьому методі критерії нумеруються в
порядку убування важливості. Нехай критерії
записані в порядку зменшення їх
важливості. Тоді повинні бути виконані наступні дії. 1-й крок. Вирішується однокритеріальна задача по 1-му критерію:
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 39/22
Метод послідовних поступок
В этом методе критерии нумеруются в
порядке убывания важности. Пусть критерии
записаны в порядке уменьшения их
важности. Тогда должны быть выполнены следующие действия.1-й шаг. Решается однокритериальная задача по 1-му критерию:
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 40/22
Метод послідовних поступок
2-й крок. Призначається розумна з інженерної
точки зору поступка ,
Ставиться і вирішується нова задача оптимізації по 2-му критерію
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 41/22
Метод послідовних поступок
3-й крок. Призначається поступка для 2-го критерію
, складається і вирішується задача оптимізації
по 3-му критерію:Процес призначення поступок по кожному критерію та рішення однокритеріальних задач триває, поки не дійдемо до
останнього K - го кроку.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 42/22
Метод послідовних поступок
K-й крок. Призначається поступка для
K-1 –
го критерію,
складається і вирішується задача оптимізації за останнім К
- м критерієм :Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 43/22
Метод послідовних поступок. Основний Недолік
полягає в
суб'єктивності вибору
контрольних показників
поступок.
При використанні методу послідовних поступок слід пам'ятати, що поступки
можуть бути несумірні між собою, тому треба попередньо організувати нормалізацію критеріїв.
Крім того, в загальному випадку вже з 2-го кроку рішення може виявитися не оптимальним за Парето.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 44/22
Метод цільового програмування
Назва цієї групи методів пов'язані з тим,
що ОПР задає певні цілі
для кожного критерія.Задача БКО перетвориться в задачу мінімізації суми відхилень з деяким показником P :
де – вагові коефіцієнти, що характеризують важливість того чи іншого критерія.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
Слайд 45/46
Метод цільового програмування
Задачу можна конкретизувати залежно від значень параметра
P і заданих цілей. Зокрема,при та
отримаємо задачу мінімізації суми квадратів відхилень :в якій мінімізується евклідова відстань від множини досяжності F до «абсолютного максимума» в просторі критеріїв. Тут
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019