Слайд 1Применение булевых функций
к релейно-контактным схемам
Слайд 2Релейно-контактные (переключательные) схемы
РКС (или ПС) устройство, состоящее из
проводников и
двухпозиционных контактов. Оно предназначается для
соединения
или разъединения полюсов источника тока с
некоторым потребителем. Контакты РКС могут быть двух
типов: замыкающие и размыкающие.
Контакты подключены к реле (переключателю).
Каждому реле ставится в соответствие своя булева
переменная xi , принимающая значение 1, при включении
реле, и 0 при его отключении.
Замыкающий контакт обозначаем через xi , размыкающий
Слайд 3Функция проводимости РКС
Всей РКС ставится в соответствие булева
функция F,
зависящая от булевых переменных x1, x2 ,
…, xn , сопоставленным
тем реле, которые имеются в схеме.
Если схема проводит ток, то функция F принимает значение 1,
в противном случае считаем, что F = 0.
Каждая РКС, в которой n независимых реле, определяет
некоторую булеву функцию F от n переменных x1, x2 , …, xn.
Функция F называется функцией проводимости этой РКС.
Теория булевых функций позволяет построить математические
модели работы реальных физических РКС.
Слайд 4Простейшие РКС и их функции проводимости
Пусть схема состоит
из двух последовательно соединенных
независимых контактов x и y
(рис.1).
Схема проводит электрический ток Û, когда оба контакта x, y
замкнуты, т.е. когда x = y = 1. Следовательно, функция
проводимости схемы конъюнкция x y.
Вторая схема состоит из двух параллельно соединенных
независимых контактов x и y (рис.2).
Очевидно функция проводимости
схемы дизъюнкция x Ú y.
Слайд 5Реализация булевых функций с помощью РКС
С помощью РКС можно
реализовать операции отрицание,
конъюнкцию и дизъюнкцию. Поэтому всякая булева
функция
может быть реализована с помощью РКС, как функция
проводимости соответствующей РКС.
Пример. Реализовать с помощью РКС эквиваленцию x y.
Представим эквиваленцию в СКНФ:
x y =
Соответствующая РКС состоит из двух последовательно
соединенных ветвей, реализующих дизъюнкии :
Слайд 6Две задачи теории РКС
1. Составление РКС с заданными условиями
работы
задача синтеза РКС.
2. Построение для заданной
булевой функции самой
простой РКС (упрощение РКС) задача анализа
РКС.
Две РКС называются равносильными, если они
имеют одинаковые функции проводимости.
Упрощая функцию проводимости РКС с помощью
равносильных преобразований, можно построить затем
более простую РКС.
Слайд 7Пример решения задачи синтеза РКС
Задача. Построить простейшую РКС по заданной
функции проводимости: F(0,0,0) = F(1,0,1) =1, иначе F =
0.
Решение: используя СДНФ, построим формулу для
функции проводимости и упростим ее:
F(x,y,z) = = .
Этой формуле соответствует РКС, изображенная на рис.4:
Слайд 8Пример решения задачи анализа РКС
Задача: упростить РКС.
Функция проводимости РКС:
F
=
=
=
Упрощенная равносильная РКС
изображена на рис. 6 .
Слайд 9Базовые логические элементы компьютера
Любые устройства компьютера, производящие обработку
или хранение
информации могут быть собраны из трех
базовых логических элементов, реализующих
коньюнкцию,
дизьюнкцию и отрицание.
На входы A и B логического элемента И,
реализующего коньюнкцию, подаются сигналы значений двух
переменных, на выходе получается значение коньюнкции:
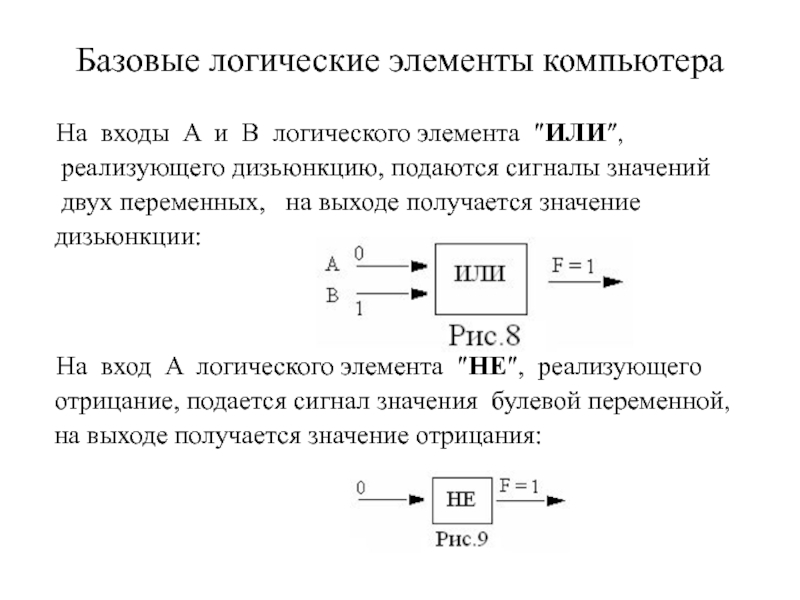
Слайд 10Базовые логические элементы компьютера
На входы A и B логического
элемента ИЛИ,
реализующего дизьюнкцию, подаются сигналы значений
двух
переменных, на выходе получается значение
дизьюнкции:
На вход A логического элемента НЕ, реализующего
отрицание, подается сигнал значения булевой переменной,
на выходе получается значение отрицания:
Слайд 11Двоичный полусумматор
Главной частью процессора является сумматор, выполняющий
сложение
двоичных чисел. При сложении цифр A и B из
первого разряда получается цифра S и возможный перенос P
во второй разряд. Таблица истинности функций S и P такова:
Очевидно, что перенос реализуется коньюнкцией: P = A B.
Используя алгоритм вычисления СКНФ для функции S,
Получаем: S = (A B) ( ) = (A B) .
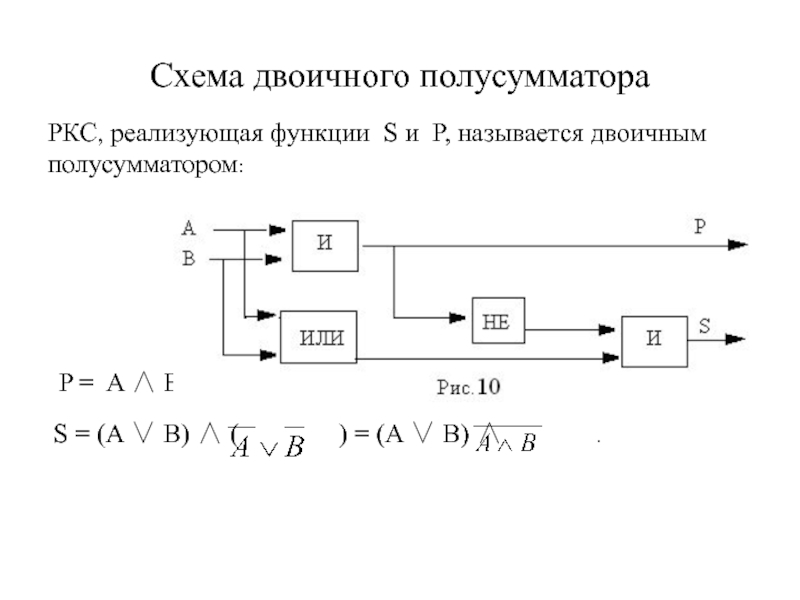
Слайд 12Схема двоичного полусумматора
РКС, реализующая функции S и P, называется двоичным
полусумматором:
P = A B.
S = (A B) ( ) = (A B) .
Слайд 13Одноразрядный сумматор
Одноразрядный сумматор должен иметь три входа:
A, B
слагаемые и перенос Pi-1 из предыдущего разряда
и
два выхода: сумма S и перенос Pi.
Pi = A B A Pi-1 B Pi-1.
S = Pi-1
Σ
сумма
перенос
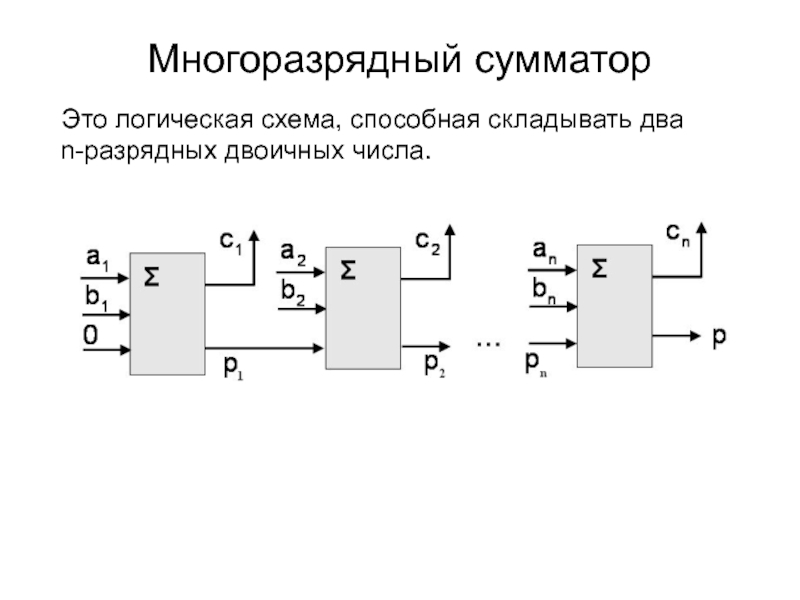
Слайд 14Многоразрядный сумматор
Это логическая схема, способная складывать два
n-разрядных двоичных числа.
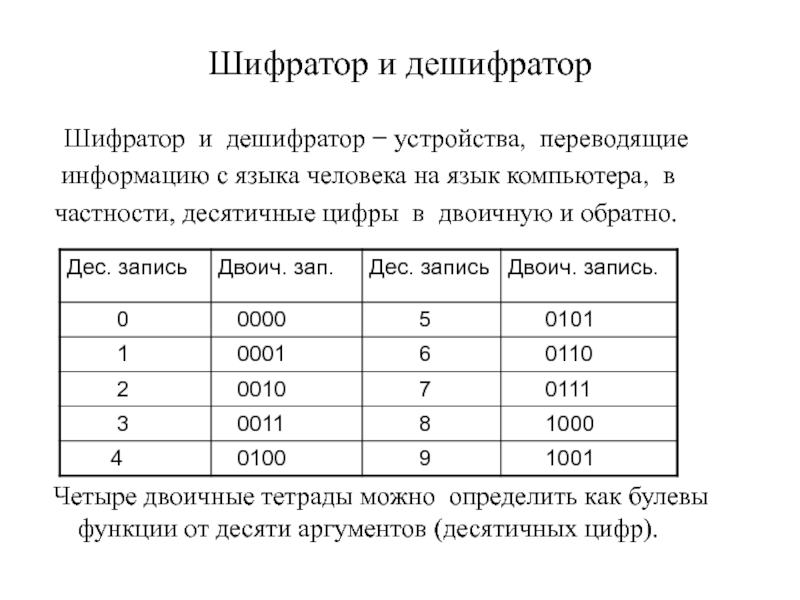
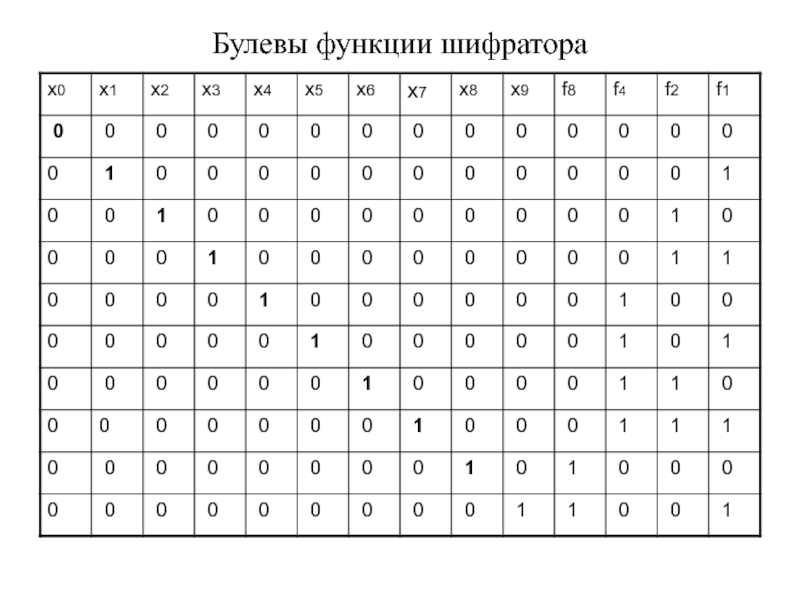
Слайд 15Шифратор и дешифратор
Шифратор и дешифратор устройства, переводящие
информацию с языка человека на язык компьютера, в
частности, десятичные цифры в двоичную и обратно.
Четыре двоичные тетрады можно определить как булевы функции от десяти аргументов (десятичных цифр).
Слайд 17Булевы функции в теории распознавания
Различные заболевания Т1, Т2,
…, Тn сопровождаются
симптомами S1, S2, …,
Sm. Определим булевы переменные:
Тогда связь между симптомами заболеваний и заболеваниями
может быть выражена на языке алгебры логики. Например,
если заболевание Тj всегда сопровождается симптомами
S2 и S3, то булева функция F = уj (х2 х3) = 1 (ТИ).
Слайд 18Булевы функции в теории распознавания
Пример:
Анализ таблицы
показывает, что во всех строках
соответствующих симптомам больного, есть
заболевание у3
и нет заболевания у1, а заболевание у2 в одних строках
есть, а в других нет. Из этого можно сделать вывод, что
относительно заболевания у2 требуются дополнительные
исследования.
Подобные ситуации встречаются в геологии, биологии
криминалистике и в других областях.
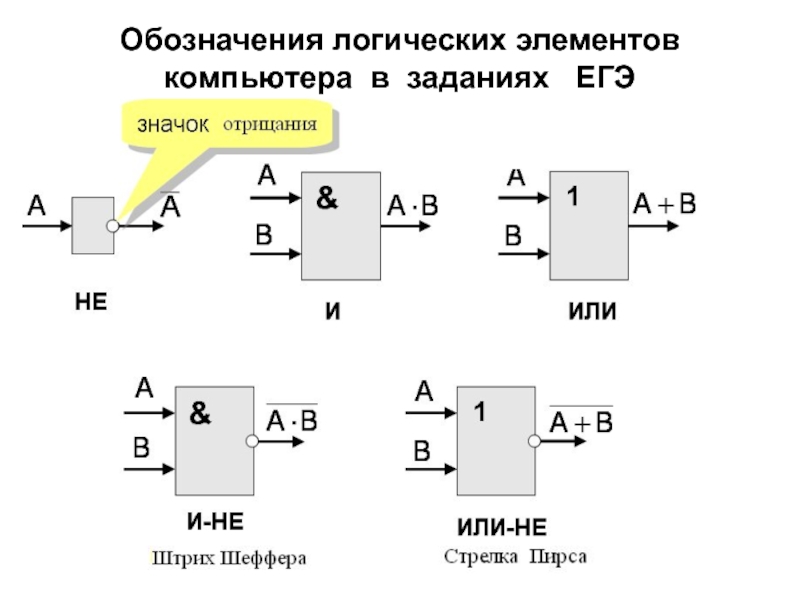
Слайд 19Обозначения логических элементов компьютера в заданиях ЕГЭ
(Штрих Шеффера)
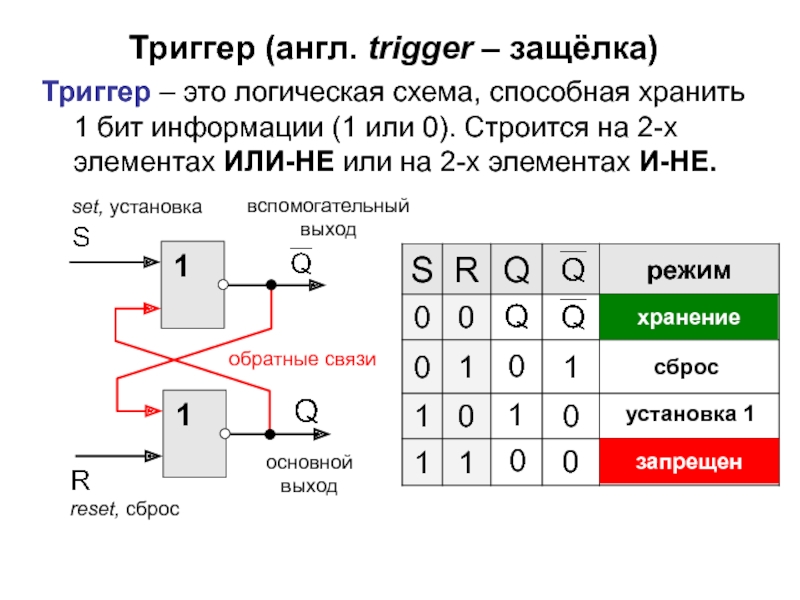
Слайд 20Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная
хранить 1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
основной
выход
вспомогательный
выход
reset, сброс
set, установка
обратные связи
1
1
0
0
0
0
Слайд 21Задача о голосовании
На соревнованиях по тяжелой атлетике каждый из трех
судей голосует “за”, нажимая на кнопку.
Постройте, по возможности,
простую схему, с помощью которой лампочка, сигнализирующая, что вес взят, зажигалась бы тогда и только тогда, когда не менее двух судей голосуют “за”.