с осями координат
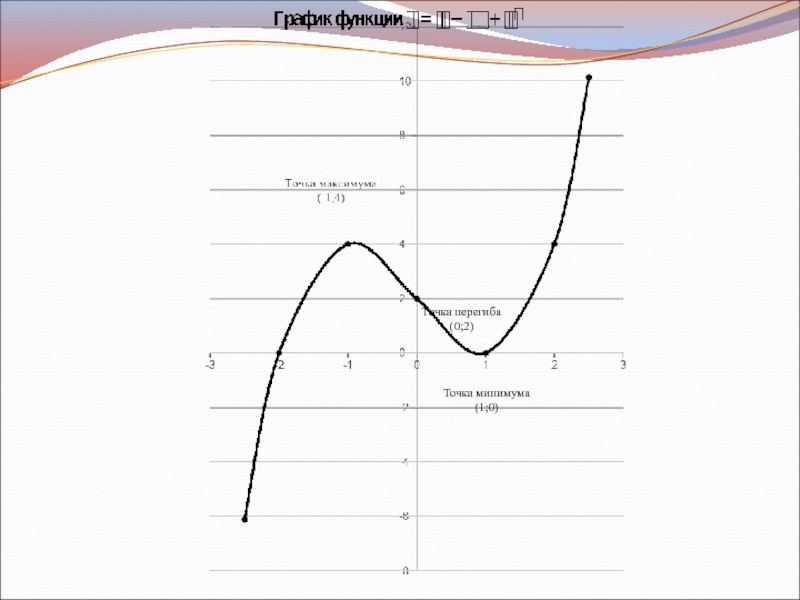
Промежутки возрастания и убывания функции; экстремумы функции
Промежутки выпуклости
и вогнутости функции; точки перегибаДополнительные точки, построение графика
Уравнение касательной в точке перегиба