Разделы презентаций

Пример -2 решения задачи № 12 контрольной работы Тема: позиционные задачи на

Содержание

Заданы поверхность прямого кругового конуса и отрезок прямой общегоположения АВS2S1A2A1B2B1

Слайды и текст этой презентации

Слайд 1Пример-2 решения задачи № 12 контрольной работы

Тема: позиционные задачи на

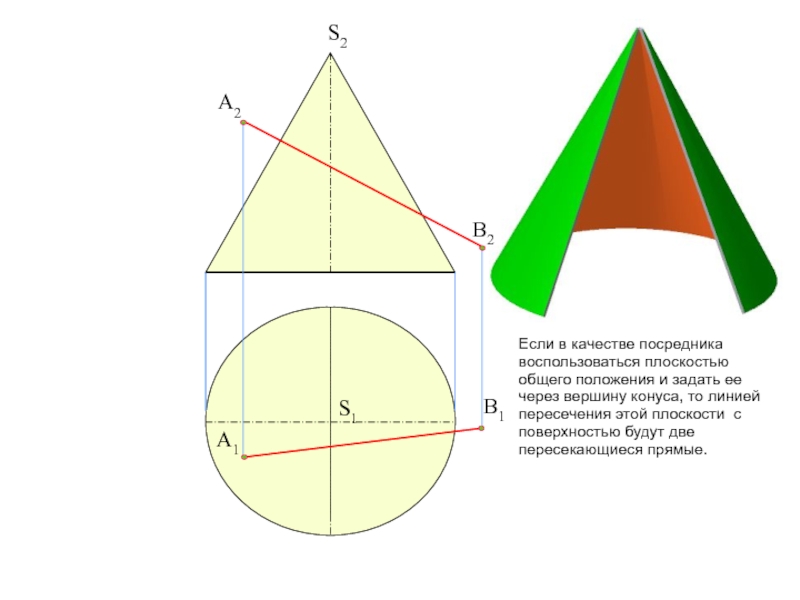
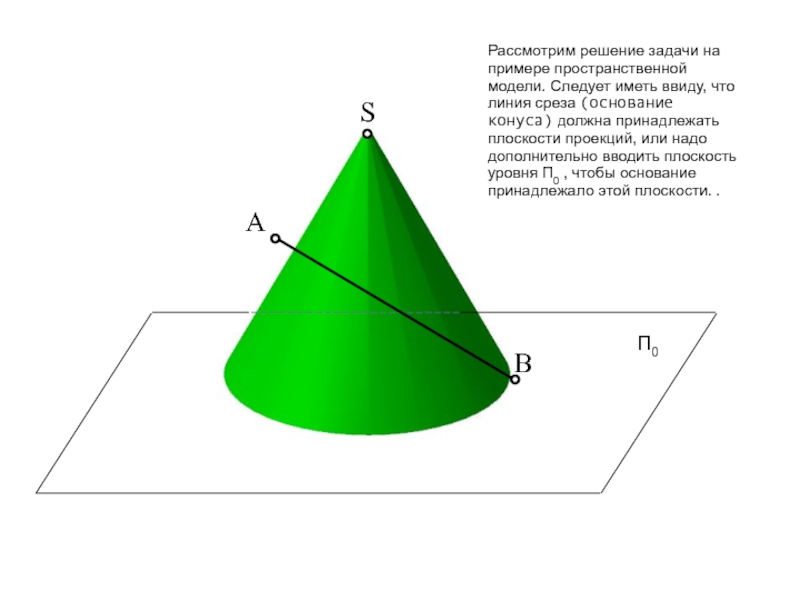
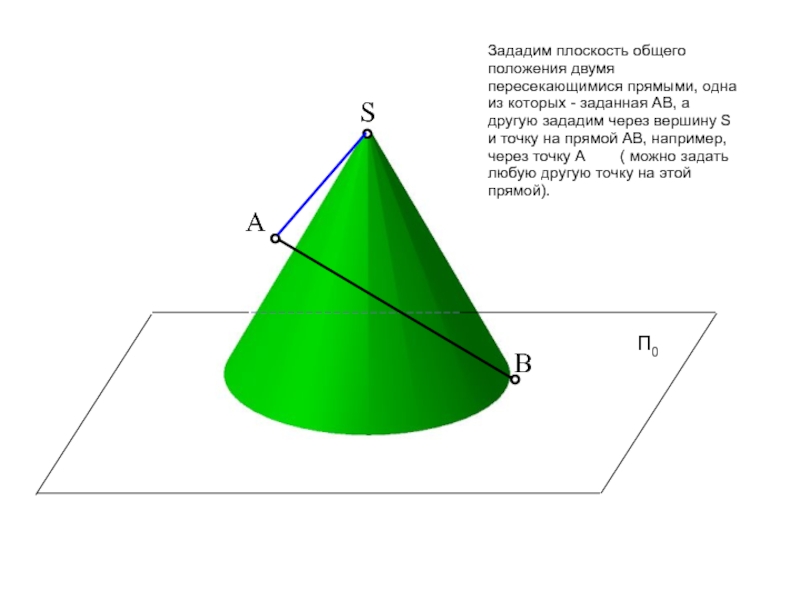
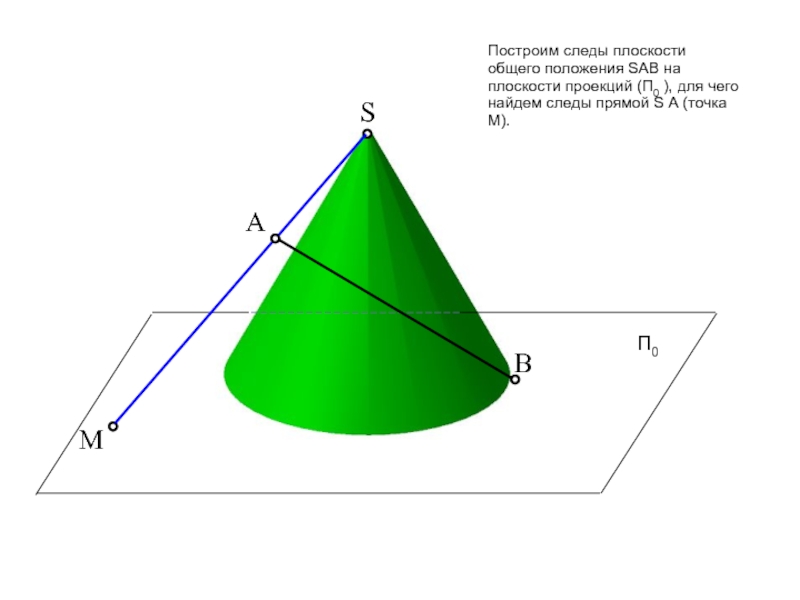
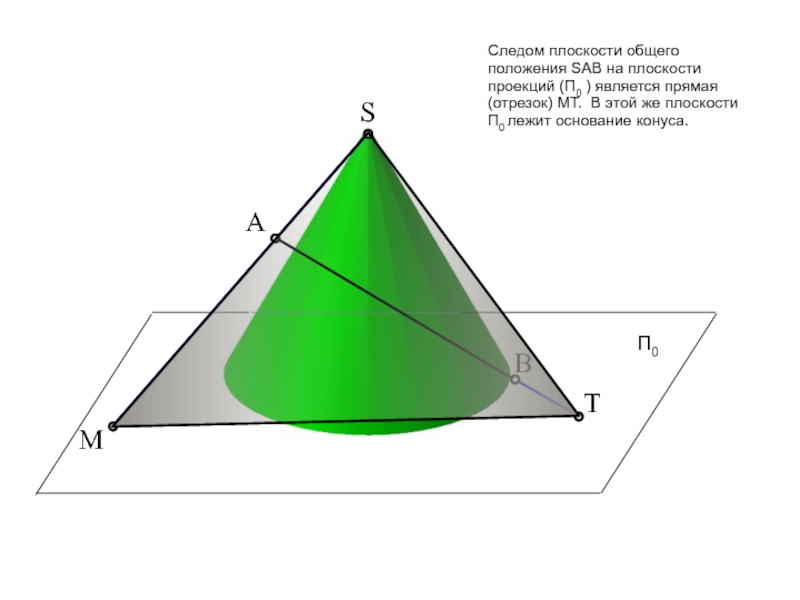
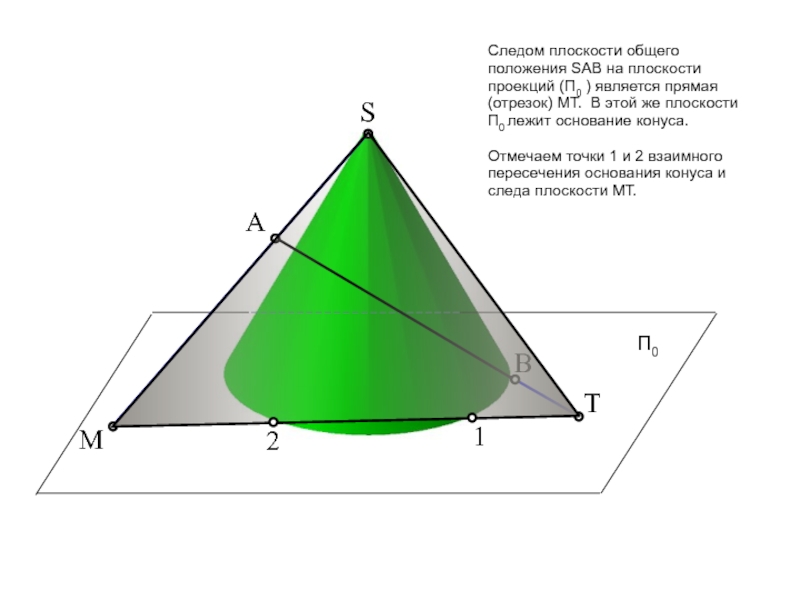
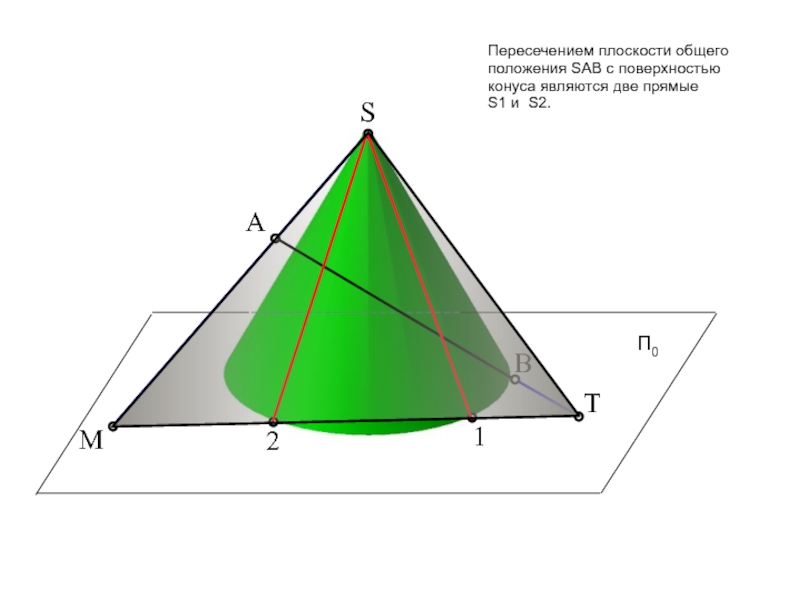
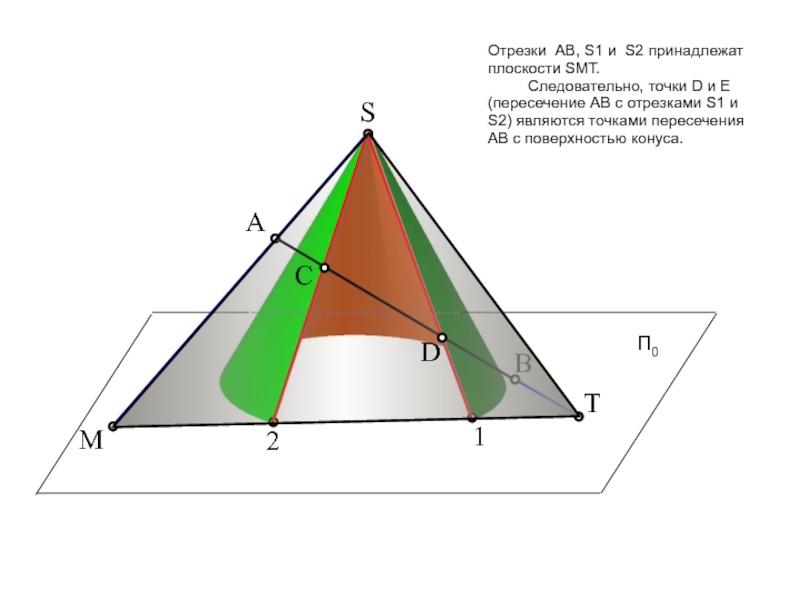
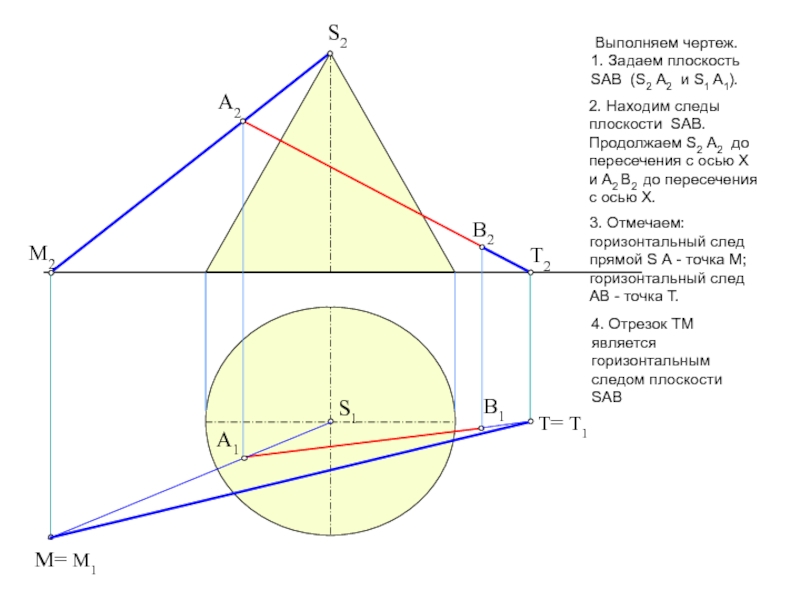
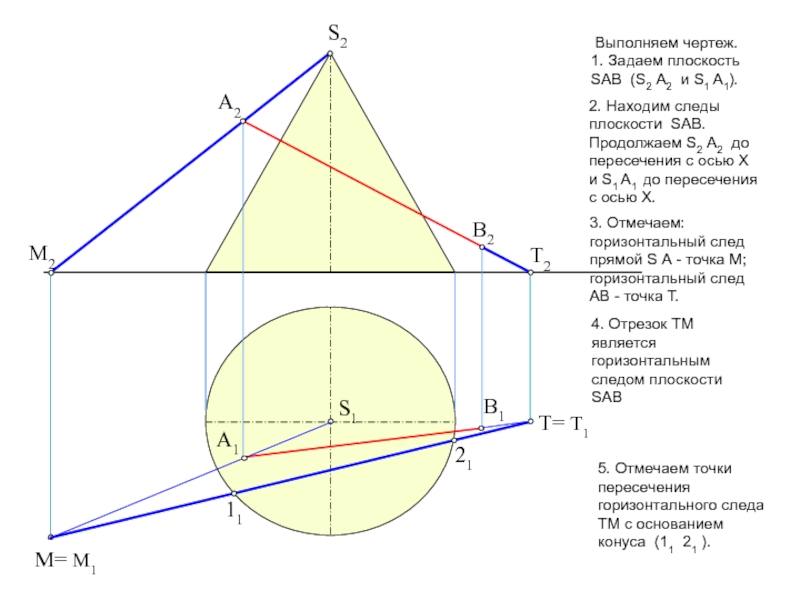
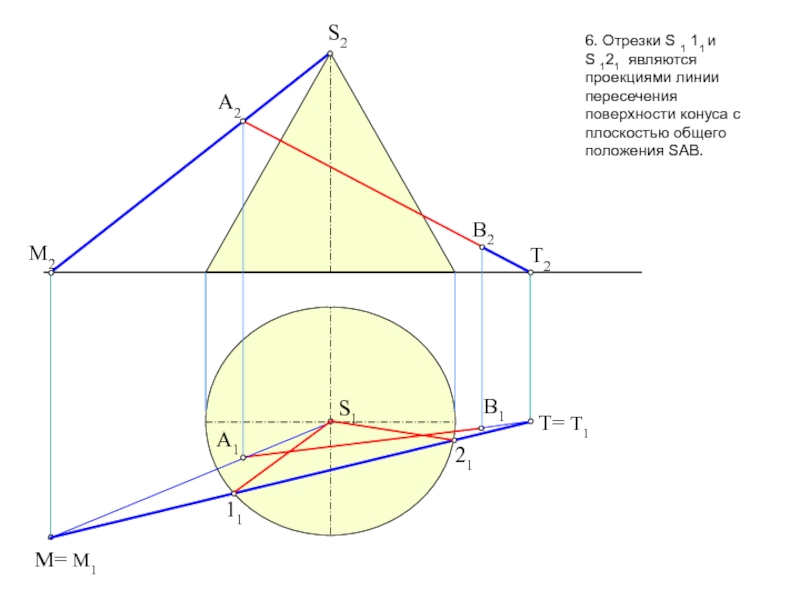
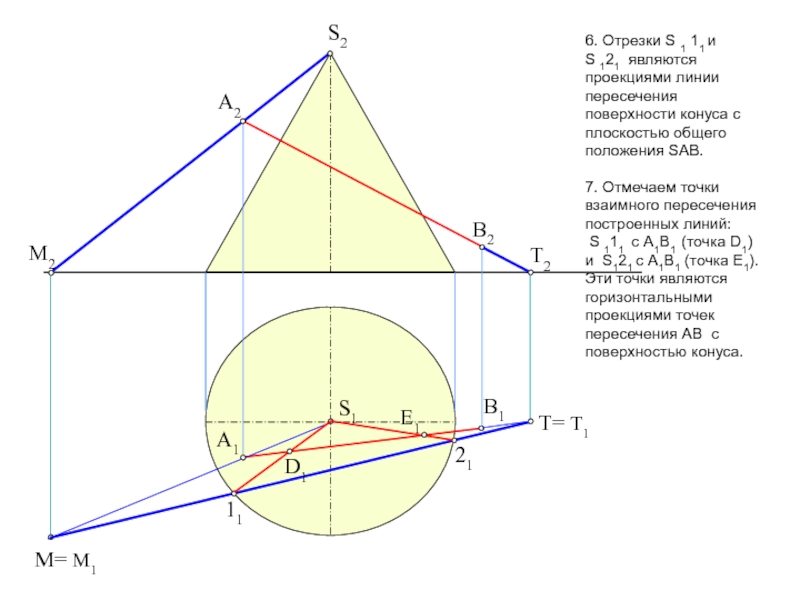
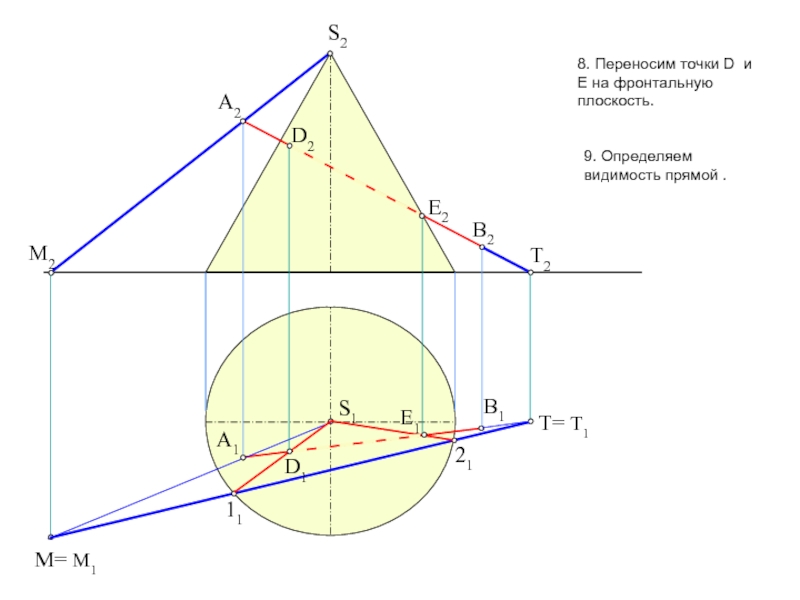
пересечение фигур. Прежде, чем приступить к решению задачи рекомендую проработать

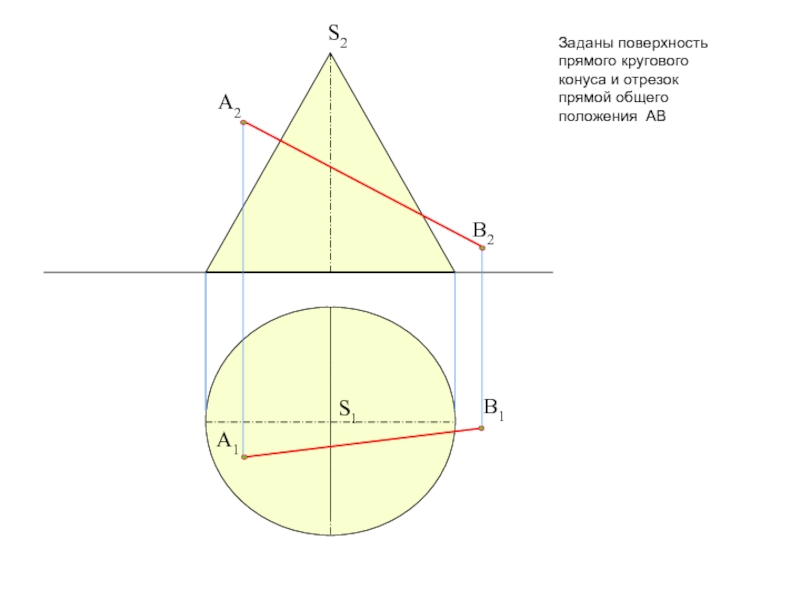
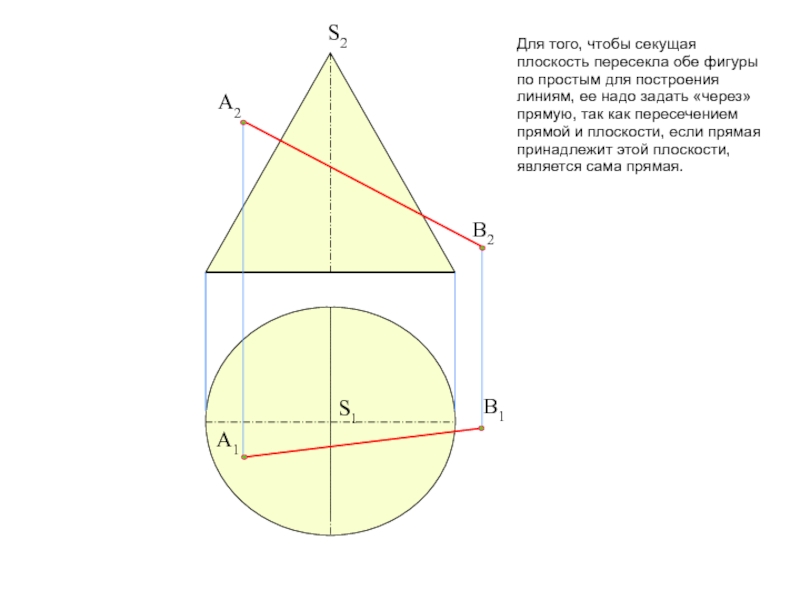
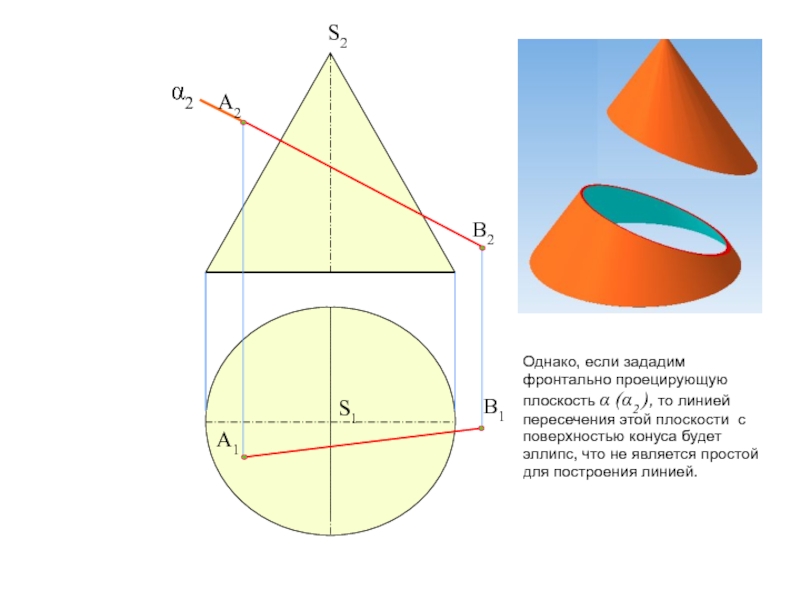
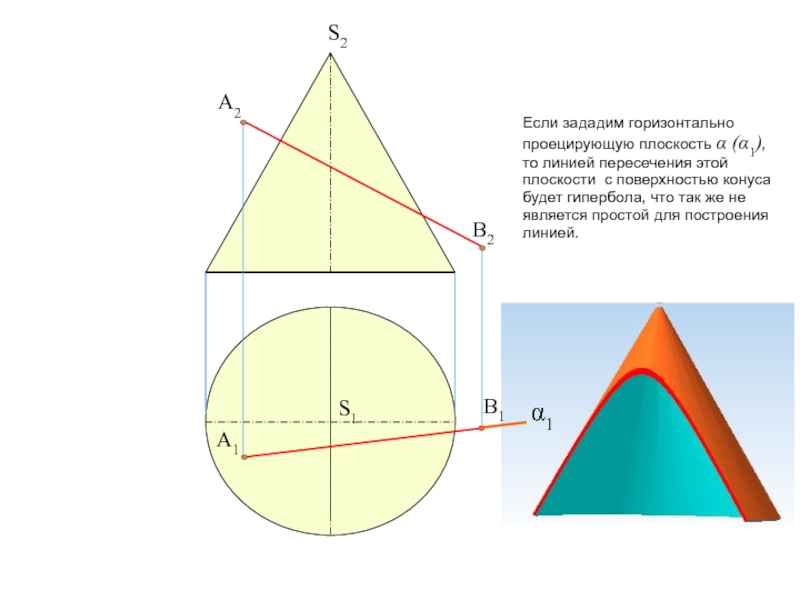
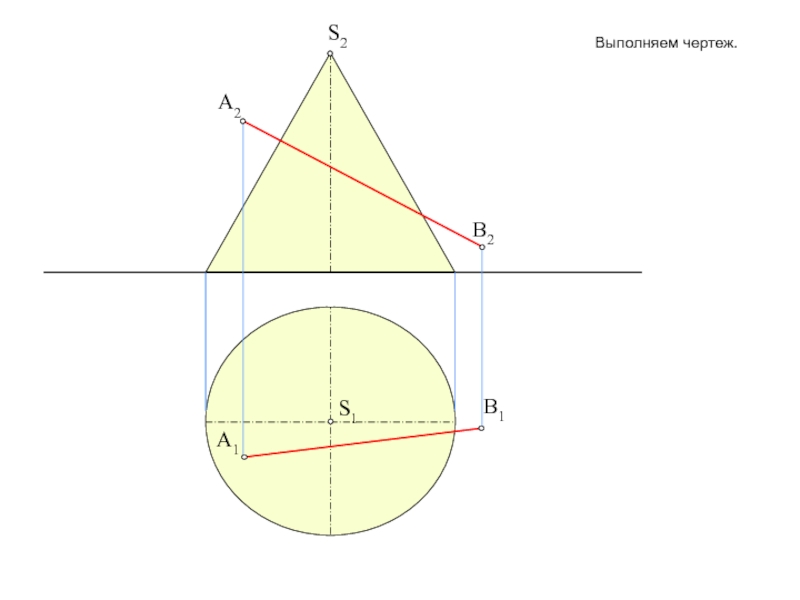
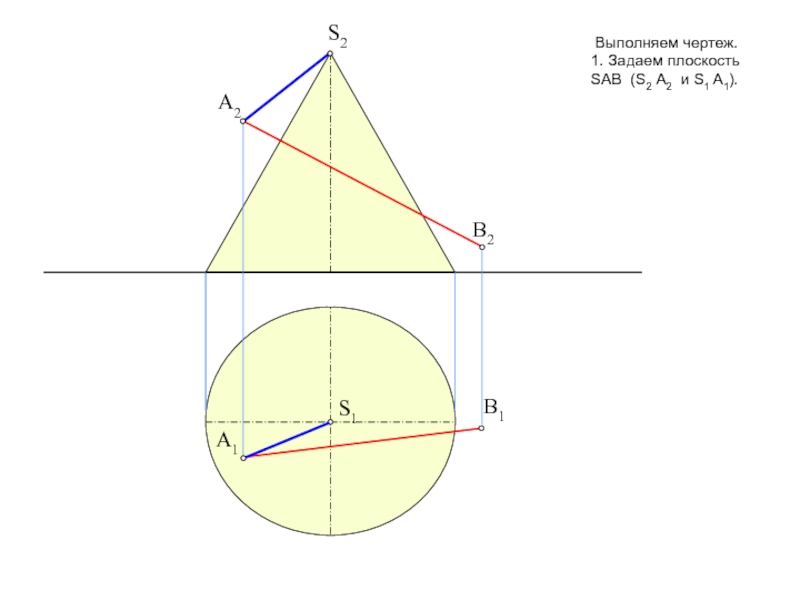
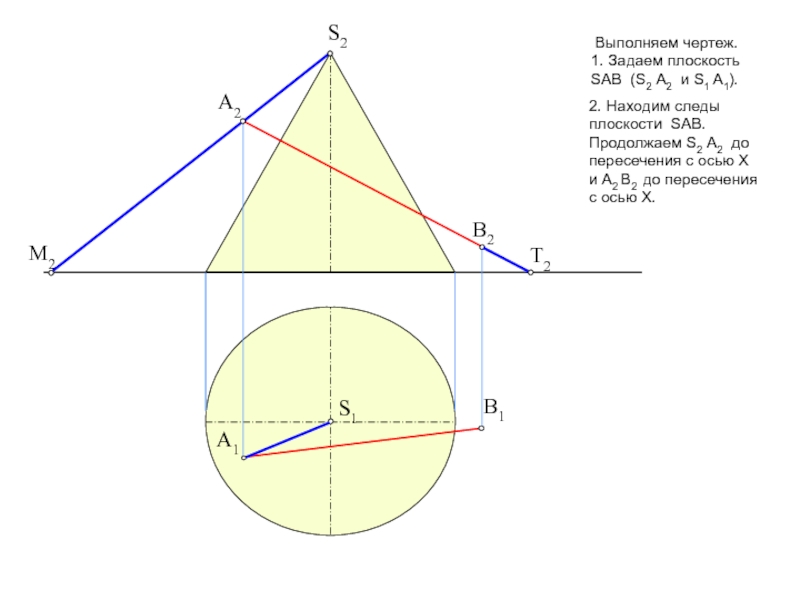
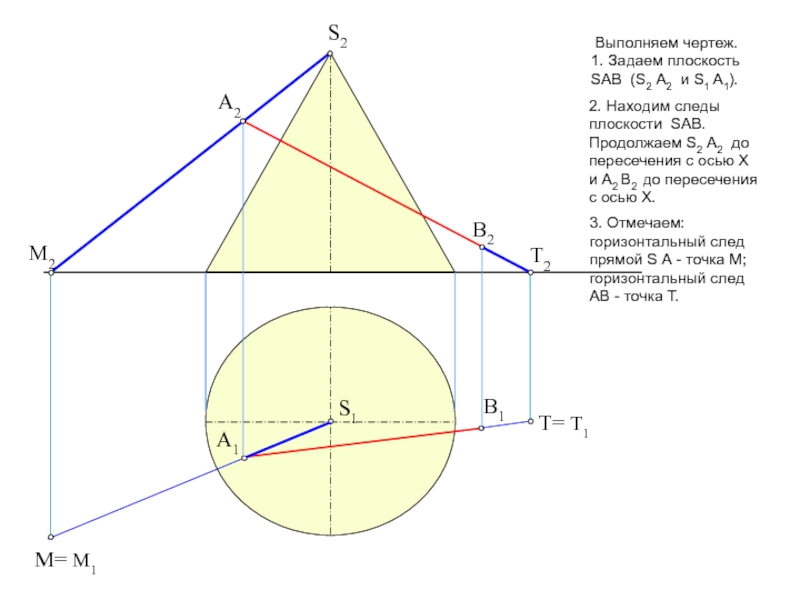
тему на форуме: «Общий алгоритм решения позиционных задач на пересечение».

Условие задачи: Определить точки пересечения прямой, заданной отрезком АВ, с поверхностью. Решить вопрос видимости прямой.
Пример-2 решения задачи № 12 контрольной работыТема: позиционные задачи на пересечение фигур. Прежде, чем приступить к решению

Слайд 2Заданы поверхность
прямого кругового
конуса и отрезок
прямой общего
положения АВ
S2
S1
A2
A1
B2
B1

Заданы поверхность прямого кругового конуса и отрезок прямой общегоположения АВS2S1A2A1B2B1

Слайд 3Для того, чтобы секущая плоскость пересекла обе фигуры по простым

для построения линиям, ее надо задать «через» прямую, так как

пересечением прямой и плоскости, если прямая принадлежит этой плоскости, является сама прямая.

S2

S1

A2

A1

B2

B1

Для того, чтобы секущая плоскость пересекла обе фигуры по простым для построения линиям, ее надо задать «через»

Слайд 4Однако, если зададим фронтально проецирующую плоскость α (α2 ), то

линией пересечения этой плоскости с поверхностью конуса будет эллипс, что

не является простой для построения линией.

α2

S2

S1

A2

A1

B2

B1

Однако, если зададим фронтально проецирующую плоскость α (α2 ), то линией пересечения этой плоскости с поверхностью конуса

Слайд 5α1
Если зададим горизонтально проецирующую плоскость α (α1), то линией пересечения

этой плоскости с поверхностью конуса будет гипербола, что так же

не является простой для построения линией.

S2

S1

A2

A1

B2

B1

α1Если зададим горизонтально проецирующую плоскость α (α1), то линией пересечения этой плоскости с поверхностью конуса будет гипербола,

Слайд 6Если в качестве посредника воспользоваться плоскостью общего положения и задать

ее через вершину конуса, то линией пересечения этой плоскости с

поверхностью будут две пересекающиеся прямые.

S2

S1

A2

A1

B2

B1

Если в качестве посредника воспользоваться плоскостью общего положения и задать ее через вершину конуса, то линией пересечения

Слайд 7S
A
B
Рассмотрим решение задачи на примере пространственной модели. Следует иметь ввиду,

что линия среза (основание конуса) должна принадлежать плоскости проекций, или

надо дополнительно вводить плоскость уровня П0 , чтобы основание принадлежало этой плоскости. .

П0

SABРассмотрим решение задачи на примере пространственной модели. Следует иметь ввиду, что линия среза (основание конуса) должна принадлежать

Слайд 8S
A
B
Зададим плоскость общего положения двумя пересекающимися прямыми, одна из которых

- заданная АВ, а другую зададим через вершину S и

точку на прямой АВ, например, через точку А ( можно задать любую другую точку на этой прямой).

П0

SABЗададим плоскость общего положения двумя пересекающимися прямыми, одна из которых - заданная АВ, а другую зададим через

Слайд 9S
A
B
M
Построим следы плоскости общего положения SАВ на плоскости проекций (П0

), для чего найдем следы прямой S А (точка М).


П0

SABMПостроим следы плоскости общего положения SАВ на плоскости проекций (П0 ), для чего найдем следы прямой S

Слайд 10S
A
B
Т
M
Построим следы плоскости общего положения SАВ на плоскости проекций (П0

), для чего найдем следы прямой S А (точка М).

И следы прямой АВ (точка Т).

П0

SABТMПостроим следы плоскости общего положения SАВ на плоскости проекций (П0 ), для чего найдем следы прямой S

Слайд 11S
A
B
Т
M
Следом плоскости общего положения SАВ на плоскости проекций (П0 )

является прямая (отрезок) МТ. В этой же плоскости П0 лежит

основание конуса.

П0

SABТMСледом плоскости общего положения SАВ на плоскости проекций (П0 ) является прямая (отрезок) МТ. В этой же

Слайд 12S
A
B
Т
M
П0
1
2
Следом плоскости общего положения SАВ на плоскости проекций (П0 )

является прямая (отрезок) МТ. В этой же плоскости П0 лежит

основание конуса.

Отмечаем точки 1 и 2 взаимного пересечения основания конуса и следа плоскости МТ.
SABТMП012Следом плоскости общего положения SАВ на плоскости проекций (П0 ) является прямая (отрезок) МТ. В этой же

Слайд 13S
A
B
Т
M
П0
1
2
Пересечением плоскости общего положения SАВ с поверхностью конуса являются две

прямые
S1 и S2.

SABТMП012Пересечением плоскости общего положения SАВ с поверхностью конуса являются две прямые S1 и S2.

Слайд 14S
A
B
Т
M
П0
1
2
Отрезки АВ, S1 и S2 принадлежат
плоскости SМТ.
Следовательно, точки D

и Е (пересечение АВ с отрезками S1 и S2) являются

точками пересечения АВ с поверхностью конуса.

C

D

SABТMП012Отрезки АВ, S1 и S2 принадлежатплоскости SМТ. Следовательно, точки D и Е (пересечение АВ с отрезками S1

Слайд 15S
A
B
Т
M
1
2
C
D
Отрезки АВ, S1 и S2 принадлежат
плоскости SМТ.
Следовательно, точки D

и Е (пересечение АВ с отрезками S1 и S2) являются

точками пересечения АВ с поверхностью конуса.

SABТM12CDОтрезки АВ, S1 и S2 принадлежатплоскости SМТ. Следовательно, точки D и Е (пересечение АВ с отрезками S1

Слайд 18 Выполняем чертеж.
S2
S1
A2
A1
B2
B1

Выполняем чертеж. S2S1A2A1B2B1

Слайд 19S2
S1
A2
A1
B2
B1
Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).

S2S1A2A1B2B1 Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1).

Слайд 20 Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).
S2
S1
A2
A1
B2
B1
M2
2. Находим следы плоскости SАВ. Продолжаем

S2 А2 до пересечения с осью Х
и А2 В2 до пересечения с осью Х.
Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1). S2S1A2A1B2B1M22. Находим следы плоскости

Слайд 21 Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).
S2
S1
A2
A1
B2
B1
M2
2. Находим следы плоскости SАВ. Продолжаем

S2 А2 до пересечения с осью Х
и А2 В2 до пересечения с осью Х.

T2

Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1). S2S1A2A1B2B1M22. Находим следы плоскости

Слайд 22 Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).
S2
S1
A2
A1
B2
B1
M2
T2
3. Отмечаем: горизонтальный след прямой S А

- точка М; горизонтальный след АВ - точка Т.

T= T1

M= M1

2. Находим следы плоскости SАВ. Продолжаем S2 А2 до пересечения с осью Х
и А2 В2 до пересечения с осью Х.

Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1). S2S1A2A1B2B1M2T23. Отмечаем: горизонтальный след

Слайд 23 Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).
S2
S1
A2
A1
B2
B1
M2
T2
3. Отмечаем: горизонтальный след прямой S А

- точка М; горизонтальный след АВ - точка Т.

T= T1

M= M1

4. Отрезок ТМ является горизонтальным следом плоскости SАВ

2. Находим следы плоскости SАВ. Продолжаем S2 А2 до пересечения с осью Х
и А2 В2 до пересечения с осью Х.

Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1). S2S1A2A1B2B1M2T23. Отмечаем: горизонтальный след

Слайд 24 Выполняем чертеж.
1. Задаем плоскость SАВ (S2 А2

и S1 А1).
S2
S1
A2
A1
B2
B1
M2
2. Находим следы плоскости SАВ. Продолжаем

S2 А2 до пересечения с осью Х
и S1 А1 до пересечения с осью Х.

T2

3. Отмечаем: горизонтальный след прямой S А - точка М; горизонтальный след АВ - точка Т.

T= T1

M= M1

21

11

5. Отмечаем точки пересечения горизонтального следа ТМ с основанием конуса (11 21 ).

4. Отрезок ТМ является горизонтальным следом плоскости SАВ

Выполняем чертеж. 1. Задаем плоскость SАВ (S2 А2 и S1 А1). S2S1A2A1B2B1M22. Находим следы плоскости

Слайд 25S2
S1
A2
A1
B2
B1
M2
T2
T= T1
M= M1
21
11
6. Отрезки S 1 11 и
S 121

являются проекциями линии пересечения поверхности конуса с плоскостью общего положения

SАВ.
S2S1A2A1B2B1M2T2T= T1M= M121116. Отрезки S 1 11 и S 121 являются проекциями линии пересечения поверхности конуса с

Слайд 26S2
S1
A2
A1
B2
B1
M2
T2
T= T1
M= M1
21
11
D1
E1
7. Отмечаем точки взаимного пересечения построенных линий:

S 111 с А1В1 (точка D1) и S121 с

А1В1 (точка Е1). Эти точки являются горизонтальными проекциями точек пересечения АВ с поверхностью конуса.

6. Отрезки S 1 11 и
S 121 являются проекциями линии пересечения поверхности конуса с плоскостью общего положения SАВ.

S2S1A2A1B2B1M2T2T= T1M= M12111D1E17. Отмечаем точки взаимного пересечения построенных линий: S 111 с А1В1 (точка D1) и

Слайд 27S2
S1
A2
A1
B2
B1
M2
T2
T= T1
M= M1
21
11
D1
E1
D2
E2
8. Переносим точки D и Е на фронтальную

плоскость.

S2S1A2A1B2B1M2T2T= T1M= M12111D1E1D2E28. Переносим точки D и Е на фронтальную плоскость.

Слайд 28S2
S1
A2
A1
B2
B1
M2
T2
T= T1
M= M1
21
11
D1
E1
D2
E2
9. Определяем видимость прямой .
8. Переносим точки

D и Е на фронтальную плоскость.

S2S1A2A1B2B1M2T2T= T1M= M12111D1E1D2E29. Определяем видимость прямой . 8. Переносим точки D и Е на фронтальную плоскость.

Похожие презентации

Особенности современных художественно-спортивных праздников Особенности современных художественно-спортивных праздников 218
SURFACE LAYER SURFACE LAYER 260
Зимин В.В машинист Турбинный цех ТЭЦ 4 автор: Зимин Илья 15 лет Зимин В.В машинист Турбинный цех ТЭЦ 4 автор: Зимин Илья 15 лет 220
Владимир Соловьев. Философия всеединства (1853 - 1900) Владимир Соловьев. Философия всеединства (1853 - 1900) 488
Аминокислоты входящие в состав Аминокислоты входящие в состав 360
Свёкла обыкновенная (Béta vulgáris) Свёкла обыкновенная (Béta vulgáris) 305
НОРМАЛЬНАЯ ЭКГ НОРМАЛЬНАЯ ЭКГ 264
Бронхиальная астма Бронхиальная астма 251
Памятка студента по подготовке к командированию в Задарский университет ( Памятка студента по подготовке к командированию в Задарский университет ( 245
ОБЩИЕ ПОНЯТИЯ ПОДТВЕРЖДЕНИЯ СООТВЕТСТВИЯ ОБЩИЕ ПОНЯТИЯ ПОДТВЕРЖДЕНИЯ СООТВЕТСТВИЯ 248
Обязанности : Математическое моделирование технологических процессов с помощью Обязанности : Математическое моделирование технологических процессов с помощью 179
Творчество Микеланджело Творчество Микеланджело 260
Строение атома Строение атома 657
Гора Петр Васильевич (1919-1988) Гора Петр Васильевич (1919-1988) 202
синусоидальный ток синусоидальный ток 888
Всероссийский конкурс молодежных проектов ЕСЛИ БЫ Я БЫЛ ПРЕЗИДЕНТОМ Всероссийский конкурс молодежных проектов ЕСЛИ БЫ Я БЫЛ ПРЕЗИДЕНТОМ 216
Аберрации Аберрации 983
Округ № 9 объединяет: 106 МКД, 10300 жителей старше 18 лет. пл. Металлургов, Округ № 9 объединяет: 106 МКД, 10300 жителей старше 18 лет. пл. Металлургов, 232
РАБОТА ФОРМИРОВАНИЙ МСГО ПРИ ВЕДЕНИИ СПАСАТЕЛЬНЫХ РАБОТ В ОЧАГАХ ПОРАЖЕНИЯ РАБОТА ФОРМИРОВАНИЙ МСГО ПРИ ВЕДЕНИИ СПАСАТЕЛЬНЫХ РАБОТ В ОЧАГАХ ПОРАЖЕНИЯ 328
История сел Стрельцы и Пушкари История сел Стрельцы и Пушкари 546

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика