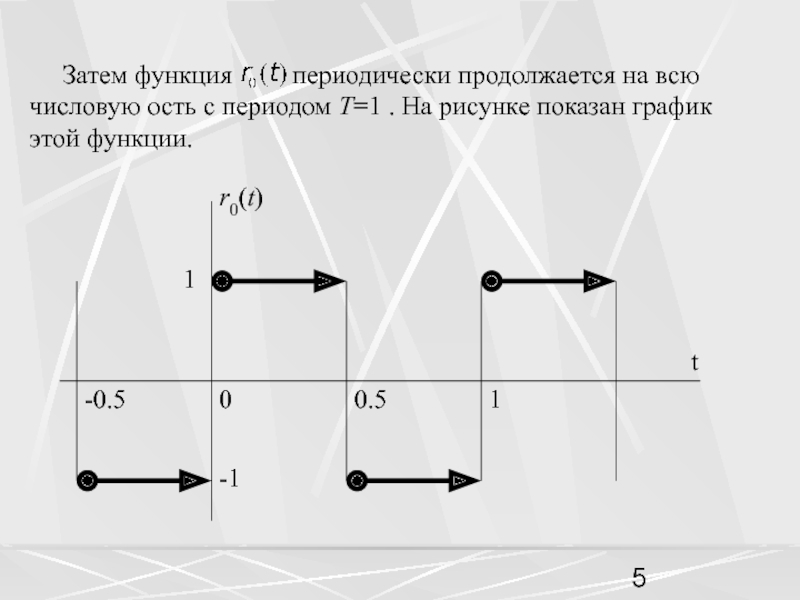
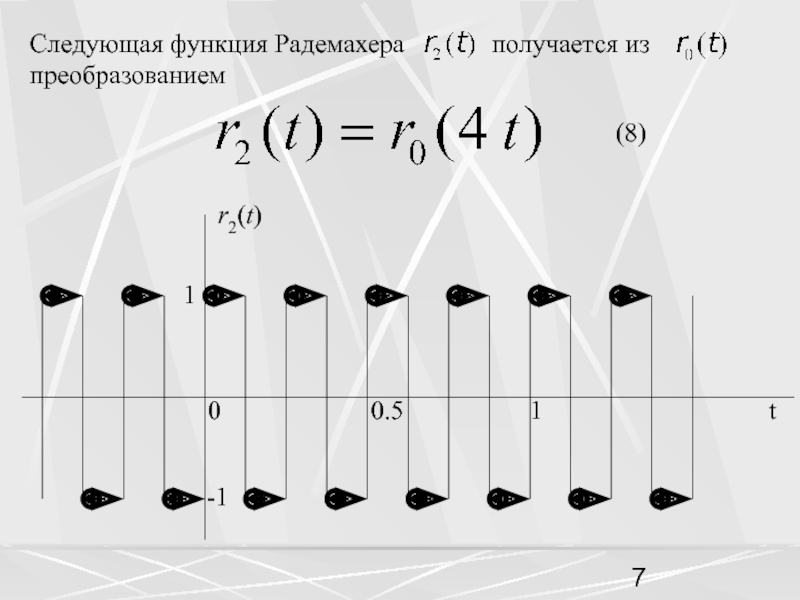
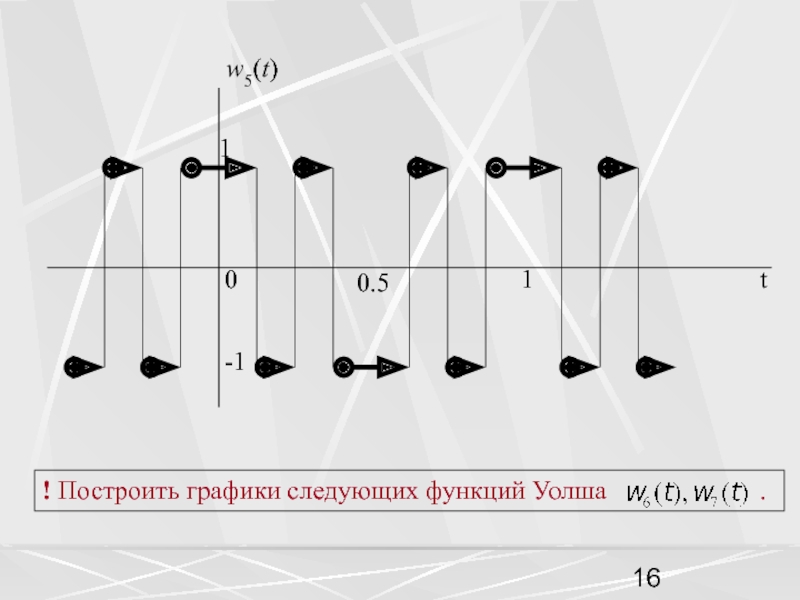
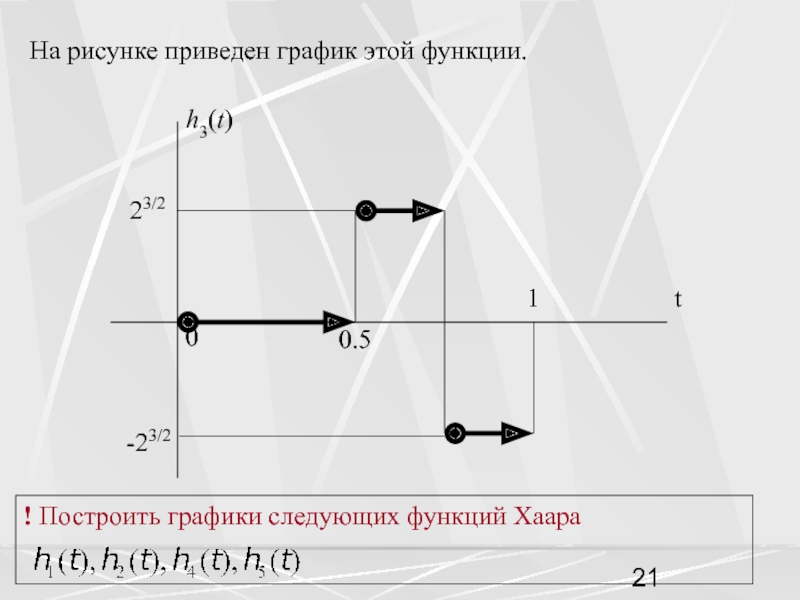
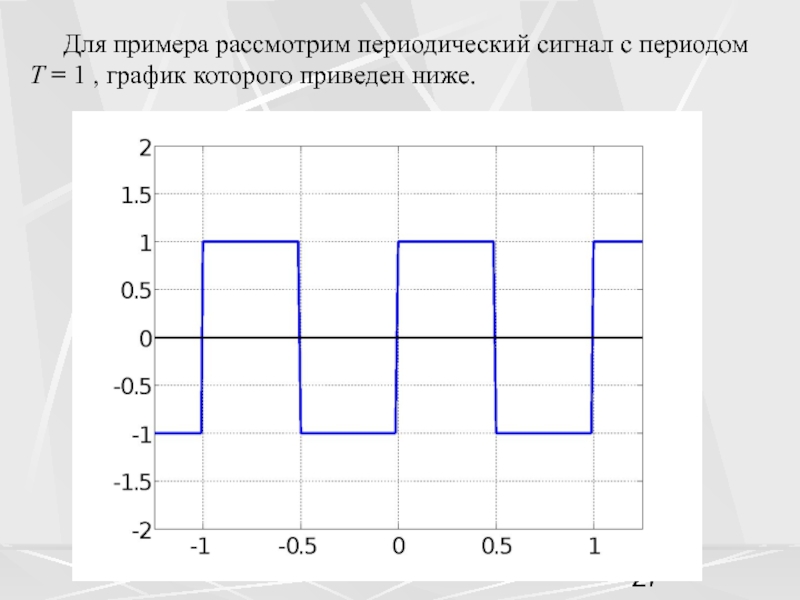
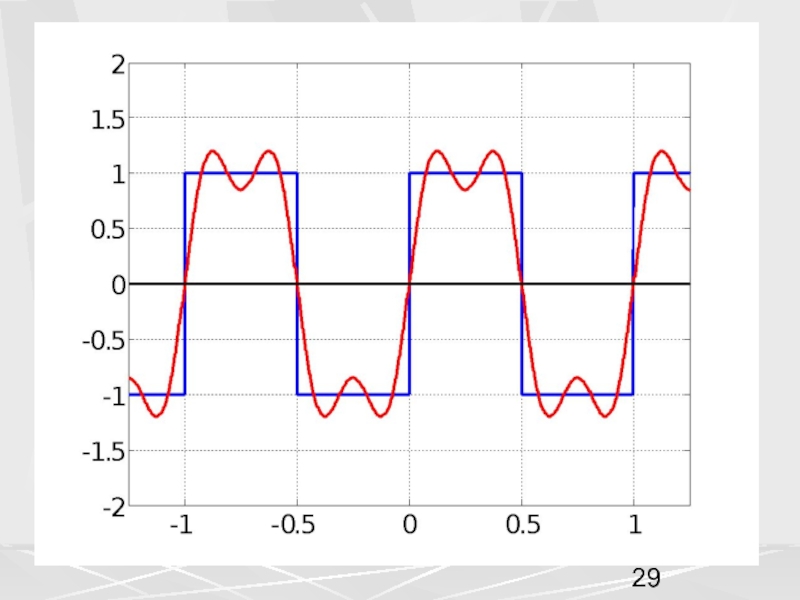
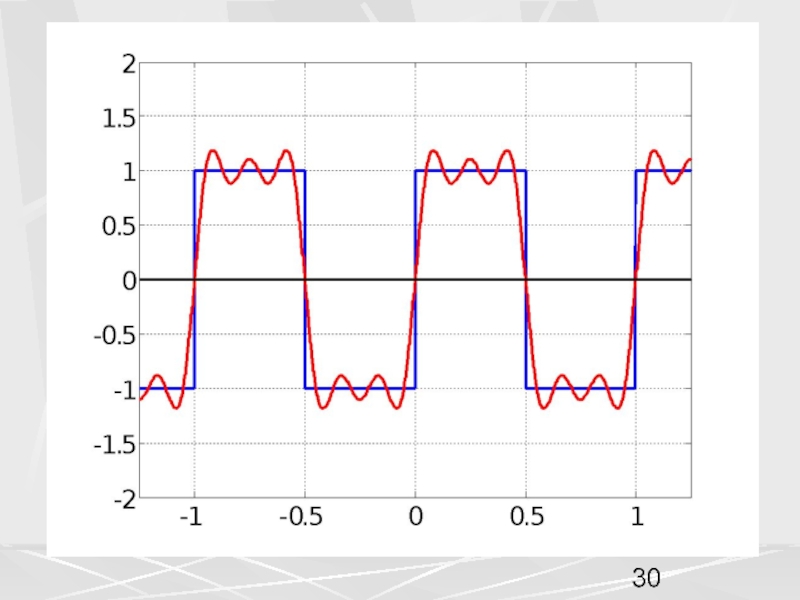
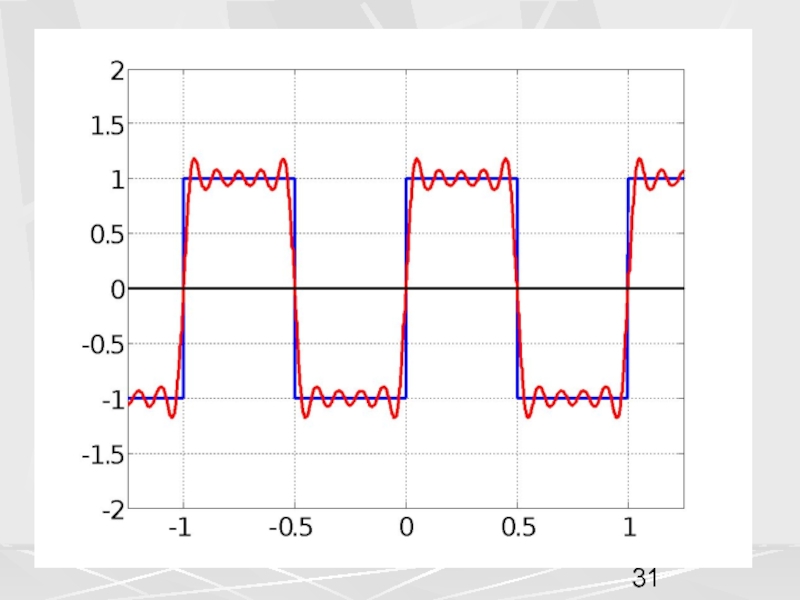
Примеры ортогональных систем в пространстве

Содержание

1. Примеры ортогональных систем в пространстве
2. Каждой функции f(t) из пространства
3. Когда говорят, что функция f(t) равна ряду
4. Система функций Радемахера В качестве
5. Затем функция
6. Следующая функция Радемахера
7. Следующая функция Радемахера получается из преобразованием (8) -1
8. Как видно график функции
9. Свойства системы Функций Радемахера 1) Система функций
10. 2) Система функций Радемахера не является полной.
11. Таким образом, система функций
12. Система функций Уолша Систему функций Уолша
13. Тогда функции системы Уолша выражаются
14. Таким образом, функция Уолша
15. На рисунках приведены графики двух функций Уолша
16. t! Построить графики следующих функций Уолша
17. Свойства системы Функций Уолша1) Система функций Уолша
18. Система функций Хаара Систему функций
19. Далее введем следующие интервалы.(16)
20. Тогда функции Хаара будут определяться следующими соотношениями (17)Например, функция задается соотношениями
21. На рисунке приведен график этой функции.! Построить графики следующих функций Хаара
22. Свойства системы Функций Хаара 1) Система функций Хаара
23. Тригонометрические ряды Фурье Рассмотрим
24. В точках разрыва ряда
25. Свойства тригонометрических рядов Фурье1) Если функция
26. 2) Если функция f(t) нечетная, то
27. Для примера рассмотрим периодический
28. Функция f(t) описывающая этот
29. Слайд 29
30. Слайд 30
31. Слайд 31
32. Слайд 32
33. Отметим следующие свойства ряда
34. 3) Вблизи точек разрыва наблюдаются пульсации, которые
35. ! Найти коэффициенты ряда Фурье для периодической
36. Комплексная форма рядов Фурье В
37. Возьмем вещественную форму ряда
38. то ряд Фурье (28) примет вид.(30)где коэффициенты
39. ! Используя формулы (22) для коэффициентов
40. Интегральное преобразование Фурье Рассмотрим переход
41. Введем дискретную частоту (33)Тогда расстояние между соседними
42. Кроме того, введем функцию
43. Далее в формулах (37) совершаем предельный переход.В результате получаем: (38)
44. В математическом анализе доказывается,
45. Спектральный анализ и преобразование Фурье
46. Из спектра S( f
47. Здесь звездочка означает комплексное
48. Третье, если сигнал вещественная нечетная функция времени,то
49. Сигнал s(t) и его
50. Свойства преобразования Фурье Кроме рассмотренных
51. 2) Изменение масштаба. Если у сигнала временной
52. Докажем второе свойство:
53. 3) Задержка сигнала. Сдвиг сигнала во времени
54. 4) Свертка сигналов. Сигнал являющийся сверткой
55. Докажем четвертое свойство:
56. 5) Произведение сигналов. Сигнал являющийся произведением двух
57. 6) Равенство Парсеваля для преобразования Фурье.
58. 7) Дифференцирование по временной области. Сигнал
59. Докажем седьмое свойство, с помощью интегрирования по частям:
60. 8) Дифференцирование в частотной области. Сигнал
61. Обобщенное преобразование Фурье Нахождение преобразования
62. Выход из этого положения
63. Далее используем интегральное представление дельта-функции.(41) Поэтому спектр сигнала есть суперпозиция дельта-функций.
64. Рассматриваемый сигнал есть действительная
65. Возьмем в качестве гармонического сигнала нечетную функцию.В этом случае получаем следующий спектр сигнала.
66. Рассматриваемый сигнал есть действительная
67. Если рассматривать произвольный периодический
68. Скачать презентанцию

Каждой функции f(t) из пространства можно поставить в соответствие ряд Фурье.где коэффициенты Фурье определяются формулами(2)(3)

Главная
Разное
Примеры ортогональных систем в пространстве

Слайды и текст этой презентации

Слайд 1Лекция 4

Примеры ортогональных систем в пространстве
Линейным

пространством называется пространство функций,

кусочно-непрерывных на отрезке t∈[a, b]. В этом пространстве скалярное произведение и норма определяются следующими формулами

Пространство является гильбертовым пространством. Это означает, что в этом пространстве существуют полные ортогональные системы функций , k=1,2,…,∞.

(1)

Лекция 4Примеры ортогональных систем в пространстве Линейным пространством называется

Слайд 2Каждой функции f(t) из пространства

можно поставить в соответствие ряд Фурье.

где коэффициенты Фурье

определяются формулами

(2)

(3)

Каждой функции f(t) из пространства можно поставить в соответствие ряд Фурье.где

Слайд 3Когда говорят, что функция f(t) равна ряду Фурье (2)

то

имеют в виду, что существует следующий предел

(4)
(5)

Слайд 4Система функций Радемахера
В качестве ортогональной системы

функций можно взять систему функций Радемахера. Система функций Радемахера

, k = 0,1,2,…,∞ является системой кусочно-постоянных функций, и определяется следующим образом. Функция на интервале t∈[0, 1) задается следующим образом.

(6)

Система функций Радемахера В качестве ортогональной системы функций можно взять систему функций Радемахера. Система функций

Слайд 5 Затем функция периодически

продолжается на всю числовую ость с периодом T=1 . На

рисунке показан график этой функции.

Затем функция периодически продолжается на всю числовую ость с периодом

Слайд 6Следующая функция Радемахера получается из функции

простым преобразованием

(7)

На рисунке показан график этой функции

Следующая функция Радемахера получается из функции

Слайд 7Следующая функция Радемахера получается

из преобразованием
(8)
-1

Слайд 8 Как видно график функции

получен из графика функции

сжатием последнего в четыре раза вдоль оси t . Отсюда получаем общее правило – функция Радемахера k-ого порядка получается из функции Радемахера нулевого порядка с помощью преобразования

(9)

а график функция Радемахера k-ого порядка получается из графика функции Радемахера нулевого порядка с помощью сжатия последнего в раз.

Как видно график функции получен из графика функции

Слайд 9Свойства системы Функций Радемахера
1) Система функций Радемахера

, k=0,1,2,…,∞ ортонормированна на отрезке t∈[0, 1]

. Другими словами, все функции Радемахера ортогональны между собой, а норма каждой из них равна единице

(10)

! Показать на частном примере k = 0, m = 1 выполнение соотношений (10)

Свойства системы Функций Радемахера 1) Система функций Радемахера , k=0,1,2,…,∞ ортонормированна

Слайд 102) Система функций Радемахера не является полной. Оказывается можно найти

элемент ψ(t) пространства

, который не совпадает ни с одной функцией Радемахера, и в тоже время ортогонален любой из функций Радемахера. Это означает, что для системы функций Радемахера не выполняется равенство Парсеваля – Стеклова . Откуда по теореме 9 (лекция 3) получаем утверждение - система функций Радемахера не является полной в пространстве . Можно показать, что в качестве элемента ψ(t) подойдет следующая функция

(11)

2) Система функций Радемахера не является полной. Оказывается можно найти элемент ψ(t) пространства

Слайд 11 Таким образом, система функций Радемахера не может

служить базисом в пространстве

, т.е. эта система функций не может использоваться для разложения в ряд Фурье.

! Показать , что для функции (11) выполняются следующие соотношения ортогональности

Таким образом, система функций Радемахера не может служить базисом в пространстве

Слайд 12Система функций Уолша
Систему функций Уолша

, n=0,1,2,…,∞ определим следующим образом. Представим целое

число n ≥ 0 в виде двоичного разложения:

(12)

Например, для числа n = 19 это будет означать следующее

Система функций Уолша Систему функций Уолша , n=0,1,2,…,∞ определим следующим

Слайд 13 Тогда функции системы Уолша выражаются при помощи функций

Радемахера как

(13)
Например, для числа n = 19 получаем следующую

функцию Уолша.

Тогда функции системы Уолша выражаются при помощи функций Радемахера как (13)Например, для числа n =

Слайд 14 Таким образом, функция Уолша

определяется как произведение функций Радемахера с номерами,

которые соответствуют единичным индексам в двоичном разложении числа n.
В таблице показан способ построения первых пяти функций Уолша.

! Найти следующие пять функций Уолша.

Таким образом, функция Уолша определяется как произведение функций

Слайд 15На рисунках приведены графики двух функций Уолша

Слайд 16t
! Построить графики следующих функций Уолша

.

Слайд 17Свойства системы Функций Уолша
1) Система функций Уолша

, k=0,1,2,…,∞ ортонормированна на отрезке

t∈[0, 1]. Поэтому имеют место соотношения

(14)

2) Система функций Уолша полна в пространстве (без доказательства).

Свойства системы Функций Уолша1) Система функций Уолша , k=0,1,2,…,∞

Слайд 18Система функций Хаара
Систему функций Хаара

, n=0,1,2,…,∞ определим на интервале

t∈[0, 1) следующим образом. Положим . Номер n следующих функций Хаара представим в виде

(15)

Формула (15) однозначно определяет числа k , m по заданному номеру n . Например,

Система функций Хаара Систему функций Хаара , n=0,1,2,…,∞ определим

Слайд 19
Далее введем следующие интервалы.

(16)

Слайд 20Тогда функции Хаара будут определяться следующими соотношениями

(17)
Например, функция

задается соотношениями

Слайд 21На рисунке приведен график этой функции.
! Построить графики следующих функций

Хаара

Слайд 22Свойства системы Функций Хаара
1) Система функций Хаара

, k=0,1,2,…,∞ ортонормированна на интервале t∈[0, 1]. Поэтому

имеют место соотношения

(18)

2) Система функций Хаара полна в пространстве (без доказательства).

Свойства системы Функций Хаара 1) Система функций Хаара , k=0,1,2,…,∞ ортонормированна на

Слайд 23Тригонометрические ряды Фурье
Рассмотрим тригонометрическую систему функций.

(19)
Как хорошо известно, из курса специальных разделов

математического анализа, такая система является полной на любом отрезке t∈[a, a+T] длины T.
Если функция f(t) имеет период T и является кусочно-гладкой функцией на периоде, то ее ряд Фурье сходится к f(t) в каждой ее точке непрерывности.

(20)

Тригонометрические ряды Фурье Рассмотрим тригонометрическую систему функций. (19) Как хорошо известно, из

Слайд 24 В точках разрыва ряда Фурье сходящегося к

среднему значению функции в этих точках.

(21)
Коэффициенты Фурье находятся по формулам:

(22)

В точках разрыва ряда Фурье сходящегося к среднему значению функции в этих точках.(21)Коэффициенты Фурье

Слайд 25Свойства тригонометрических рядов Фурье
1) Если функция f(t) четная, то

из интегралов (22) видно, что коэффициенты

, и возникает разложение по косинусам

(23)

Свойства тригонометрических рядов Фурье1) Если функция f(t) четная, то из интегралов (22) видно, что коэффициенты

Слайд 262) Если функция f(t) нечетная, то из интегралов (22)

видно, что в этом случае коэффициенты

, и возникает разложение по синусам

(24)

2) Если функция f(t) нечетная, то из интегралов (22) видно, что в этом случае коэффициенты

Слайд 27 Для примера рассмотрим периодический сигнал с периодом

T = 1 , график которого приведен ниже.

Для примера рассмотрим периодический сигнал с периодом T = 1 , график которого приведен

Слайд 28 Функция f(t) описывающая этот сигнал является, во-первых,

нечетной функцией, во-вторых, она имеет разрывы в точках t =

n/2 , n ∈ Z. Поэтому ряд Фурье для этой функции будем вычислять по синусам (24). Коэффициенты разложения в этом случае равны

(25)

Рассмотрим, как описывают частные суммы ряда Фурье выбранный сигнал.

(26)

Функция f(t) описывающая этот сигнал является, во-первых, нечетной функцией, во-вторых, она имеет разрывы в

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33 Отметим следующие свойства ряда Фурье, которые видны

из этих графиков
1) С увеличением числа членов N частные

суммы все точнее описывают сигнал, за исключением областей вблизи точек разрыва.
2) Выполняется свойство, о котором говорилось выше – в точке разрыва ряд Фурье сходится к среднему значению в точке разрыва. Например, в точке t = 0 мы имеем

Отметим следующие свойства ряда Фурье, которые видны из этих графиков1) С увеличением числа

Слайд 343) Вблизи точек разрыва наблюдаются пульсации, которые не пропадают с

увеличением числа членов ряда N , пульсации лишь сжимаются, приближаясь

к точке разрыва. Это явление, присущее рядам Фурье для любых сигналов с разрывами первого рода (скачками), называется эффектом Гиббса.

! Найти коэффициенты ряда Фурье для периодической f(t) функции с периодом T = 1 , и заданной на периоде следующими соотношениями.

Написать программу в пакете MATLAB и построить графики частных сумм ряда Фурье.

3) Вблизи точек разрыва наблюдаются пульсации, которые не пропадают с увеличением числа членов ряда N , пульсации

Слайд 35! Найти коэффициенты ряда Фурье для периодической f(t) функции с

периодом T = 1 , и заданной на периоде следующим

соотношением.

Написать программу в пакете MATLAB и построить графики частных сумм ряда Фурье.

! Найти коэффициенты ряда Фурье для периодической f(t) функции с периодом T = 1 , и заданной на периоде следующим соотношением.

Написать программу в пакете MATLAB и построить графики частных сумм ряда Фурье.

! Найти коэффициенты ряда Фурье для периодической f(t) функции с периодом T = 1 , и заданной

Слайд 36Комплексная форма рядов Фурье
В радиотехнике наиболее употребительной

является комплексная форма ряда Фурье. Эта форма возникает из вещественной

формы ряда Фурье, если использовать формулы Эйлера.

(27)

Комплексная форма рядов Фурье В радиотехнике наиболее употребительной является комплексная форма ряда Фурье. Эта форма

Слайд 37 Возьмем вещественную форму ряда Фурье (20) и

подставим в нее формулы (27).

(28)
Если ввести следующие обозначения:

(29)

Возьмем вещественную форму ряда Фурье (20) и подставим в нее формулы (27).(28)Если ввести следующие

Слайд 38то ряд Фурье (28) примет вид.

(30)
где коэффициенты

комплексного ряда Фурье будут определяться формулой.

(31)

Слайд 39! Используя формулы (22) для коэффициентов ,

вещественного ряда Фурье, показать справедливость формулы (31) для коэффициентов

комплексного ряда Фурье.
! Найти коэффициенты комплексного ряда Фурье для периодической f(t) функции с периодом T = 1 , и заданной на периоде следующими соотношениями.

! Найти коэффициенты комплексного ряда Фурье для периодической f(t) функции с периодом T = 1 , и заданной на периоде следующим соотношением.

! Используя формулы (22) для коэффициентов , вещественного ряда Фурье, показать справедливость формулы

Слайд 40Интегральное преобразование Фурье
Рассмотрим переход от ряда Фурье

в комплексной форме (30, 31) к интегральному преобразованию Фурье с

помощью предельного перехода, когда период стремиться к бесконечности T → ∞. Перепишем комплексный ряд Фурье, заменив функцию f(t) на функцию s(t) – так мы на первых лекция обозначали сигнал, а буквой f будем обозначать частоту.

(32)

Интегральное преобразование Фурье Рассмотрим переход от ряда Фурье в комплексной форме (30, 31) к интегральному

Слайд 41Введем дискретную частоту

(33)
Тогда расстояние между соседними частотами Δf будет

равно

(34)
Когда период T стремиться к бесконечности, величина

Δf стремиться к нулю. Поэтому дискретная частота в пределе будет меняться непрерывным образом на всей числовой оси. Поэтому в пределе T → ∞ мы заменим дискретную частоту на непрерывную частоту f .

(35)

Введем дискретную частоту (33)Тогда расстояние между соседними частотами Δf будет равно(34) Когда период T стремиться

Слайд 42 Кроме того, введем функцию

от дискретной частоты по формуле

(36)
Подставляя

соотношения (33, 34, 36) в формулы ряда Фурье в комплексной форме (32), получаем.

(37)

Кроме того, введем функцию от дискретной частоты по

Слайд 43Далее в формулах (37) совершаем предельный переход.

В результате получаем:

(38)

Слайд 44 В математическом анализе доказывается, что преобразование Фурье

(38) справедливо для функций s(t) удовлетворяющих следующим условиям.
1) Функция

s(t) должна быть абсолютно интегрируемой на всей числовой оси, т.е.

2) Функция должна быть кусочно-гладкая на любом конечном интервале.

В математическом анализе доказывается, что преобразование Фурье (38) справедливо для функций s(t) удовлетворяющих следующим

Слайд 45Спектральный анализ и преобразование Фурье
Кроме временного представления

сигналов, где сигнал это функция времени s( t ), при

анализе и обработке сигналов, используется также частотное представление сигнала в виде функции частоты S( f ) . Функции s( t ) и S( f ) связаны друг с другом преобразованием Фурье. (38)
Здесь второе выражение называется прямое преобразование Фурье, а первое выражение называется обратное преобразование Фурье. Функция S( f ) называется спектром сигнала s( t ).
Функция S( f ) является комплексной функцией, и может быть представлена в алгебраической и показательной форме.

Спектральный анализ и преобразование Фурье Кроме временного представления сигналов, где сигнал это функция времени s(

Слайд 46 Из спектра S( f ) можно получить

амплитудно-частотную характеристику (АЧХ) A( f ) и фазово-частотную характеристику (ФЧХ) ϕ( f

) сигнала, с помощью соотношений.

(39)

Отметим некоторые из свойств, преобразования Фурье. Первое, если сигнал вещественная функция, то для спектра S( f ) выполняются следующие соотношения четности

Из спектра S( f ) можно получить амплитудно-частотную характеристику (АЧХ) A( f ) и фазово-частотную характеристику

Слайд 47
Здесь звездочка означает комплексное сопряжение. Из этих

соотношений видно, что для вещественного сигнала, АЧХ - четная функция,

а ФЧХ – нечетная функция.
Второе, если сигнал вещественная четная функция времени

то для спектра выполняются следующие соотношения

Здесь звездочка означает комплексное сопряжение. Из этих соотношений видно, что для вещественного сигнала, АЧХ

Слайд 48Третье, если сигнал вещественная нечетная функция времени

,
то для спектра выполняются

следующие соотношения

Здесь действительная часть спектра равна нулю.

Третье, если сигнал вещественная нечетная функция времени,то для спектра выполняются следующие соотношенияЗдесь действительная часть спектра равна нулю.

Слайд 49 Сигнал s(t) и его частотный спектр S(f)

взаимно однозначно соответствуют друг другу через прямое и обратное преобразование

Фурье. Это соответствие будем обозначать следующим образом

Сигнал s(t) и его частотный спектр S(f) взаимно однозначно соответствуют друг другу через прямое

Слайд 50Свойства преобразования Фурье
Кроме рассмотренных выше свойств

спектра, преобразование Фурье обладает целым рядом полезных свойств для прикладных

задач.
1) Линейность. Линейной комбинации сигналов, соответствует линейная комбинация спектров.

Свойства преобразования Фурье Кроме рассмотренных выше свойств спектра, преобразование Фурье обладает целым рядом полезных свойств

Слайд 512) Изменение масштаба. Если у сигнала временной масштаб уменьшается в

a раз, то у спектра частотный масштаб возрастает в a

раз.

Слайд 52Докажем второе свойство:

Слайд 533) Задержка сигнала. Сдвиг сигнала во времени приводит к умножению

спектра на фазовый множитель.

! Доказать свойство линейности преобразования Фурье.
! Доказать

свойство задержки сигнала в преобразовании Фурье.

3) Задержка сигнала. Сдвиг сигнала во времени приводит к умножению спектра на фазовый множитель.! Доказать свойство линейности

Слайд 544) Свертка сигналов. Сигнал являющийся сверткой двух других сигналов

имеет спектр равный произведению спектров исходных сигналов.

Слайд 55Докажем четвертое свойство:

Слайд 565) Произведение сигналов. Сигнал являющийся произведением двух других сигналов имеет

спектр равный свертке спектров исходных сигналов

! Доказать свойство произведения сигналов

в преобразовании Фурье.

5) Произведение сигналов. Сигнал являющийся произведением двух других сигналов имеет спектр равный свертке спектров исходных сигналов! Доказать

Слайд 576) Равенство Парсеваля для преобразования Фурье. Для преобразования Фурье

имеет место следующее интегральное равенство (равенство Парсеваля).

(40)
Докажем шестое свойство:

6) Равенство Парсеваля для преобразования Фурье. Для преобразования Фурье имеет место следующее интегральное равенство (равенство Парсеваля).

Слайд 587) Дифференцирование по временной области. Сигнал являющийся производной от

другого сигнала имеет спектр равный спектру исходного сигнала умноженному на

частоту и коэффициент (2 π i ) .

7) Дифференцирование по временной области. Сигнал являющийся производной от другого сигнала имеет спектр равный спектру исходного

Слайд 59 Докажем седьмое свойство, с помощью интегрирования по

частям:

Слайд 608) Дифференцирование в частотной области. Сигнал являющийся произведением другого

сигнала на время и коэффициент (– 2 π i )

имеет спектр равный производной по частоте от спектра исходного сигнала.

! Доказать восьмое свойство преобразования Фурье.

8) Дифференцирование в частотной области. Сигнал являющийся произведением другого сигнала на время и коэффициент (– 2

Слайд 61Обобщенное преобразование Фурье
Нахождение преобразования Фурье для периодических

сигналов вызывает некоторые затруднения. Дело в том, что любой периодический

сигнал является инфинитным, т.е. отличен от нуля на всем временном интервале −∞ < t < ∞ .
Поэтому нарушается основное условие существования преобразования Фурье:

Обобщенное преобразование Фурье Нахождение преобразования Фурье для периодических сигналов вызывает некоторые затруднения. Дело в том,

Слайд 62 Выход из этого положения состоит в переходе

к обобщенному преобразованию Фурье, где используется дельта-функция. Покажем это на

примере.
Рассмотрим спектр периодического сигнала. Пусть это будет гармонический сигнал с частотой .

Используя формулу Эйлера просто получить спектр этого сигнала.

Выход из этого положения состоит в переходе к обобщенному преобразованию Фурье, где используется дельта-функция.

Слайд 63Далее используем интегральное представление дельта-функции.

(41)
Поэтому спектр сигнала есть суперпозиция

дельта-функций.

Слайд 64 Рассматриваемый сигнал есть действительная четная функция, поэтому

по всем правилам мнимая часть спектра равна нулю, действительная часть

показана на рисунке.

Рассматриваемый сигнал есть действительная четная функция, поэтому по всем правилам мнимая часть спектра равна

Слайд 65Возьмем в качестве гармонического сигнала нечетную функцию.

В этом случае получаем

следующий спектр сигнала.

Слайд 66 Рассматриваемый сигнал есть действительная нечетная функция, поэтому

действительная часть спектра равна нулю, мнимая часть спектра показана на

рисунке

Рассматриваемый сигнал есть действительная нечетная функция, поэтому действительная часть спектра равна нулю, мнимая часть

Слайд 67 Если рассматривать произвольный периодический сигнал, то, как

известно, его можно разложить в ряд Фурье. Поэтому любой периодический

сигнал есть суперпозиция синусов и косинусов с разными частотами и спектр любого периодического сигнала есть сумма дельта-функций с разными частотами и разными амплитудами. График спектра в этом случае представляет собой набор стрелок разной длины и направленных вверх или вниз. Такой спектр называют линейчатым спектром.
Рассмотренные ранее спектры называют сплошным спектром. Для линейчатого спектра не имеет смысл ФЧХ как функция частоты ϕ( f ). АЧХ периодических сигналов имеет линейчатую структуру.

Если рассматривать произвольный периодический сигнал, то, как известно, его можно разложить в ряд Фурье.

Скачать презентацию

Разделы презентаций