Слайд 1Лекция № 6
Примеры разработки параллельных алгоритмов (реальная оптимизация)
Слайд 2Распараллеливание циклов
Как правило в любом программном коде основным объектом распараллеливания
являются циклы.
Поэтому крайне важно тщательно изучать структуру этих циклов,
определяя, какие из них можно распараллелить, а какие нет.
Рассмотрим конкретные примеры циклов, используя как пример процедуры оптимизации языка Фортран
Слайд 3Распараллеливание циклов
Оптимизируются, как правило, следующие операции параллельного и векторного режимов:
операции
с массивами, выполняемые в векторно-параллельном (ВП) режиме
интерактивные циклы DO вида
DO i = 1,N.
Такие циклы не должны содержать ни операторов, ни зависимостей данных, ограничивающих оптимизацию выполнения цикла векторно-параллельном режиме.
Циклы DO в зависимости от определенных ограничений могут выполняться в векторном, скалярном параллельном или скалярном режимах.
Циклы DO могут быть представлены в виде нескольких циклов, некоторые из которых реализуются в скалярном режиме, а другие в зависимости от ограничений подвергаются оптимизации определенного вида
Слайд 4Распараллеливание циклов
циклы DO WHILE, не содержащие недопустимых операторов и зависимостей
данных выполняются в скалярном параллельном режиме.
все другие программы выполняются в
скалярном режиме. Отметим, что последовательность скалярных операций с элементами некоторого массива не оптимизируется.
Пример программы, которая не будет выполняться ни в параллельном, ни в векторном режимах:
A(1) = A(1)+S
A(2) = A(2)+S
A(3) = A(3)+S
A(4) = A(4)+S
Слайд 5Режимы выполнения программ
Скалярный режим. В этом режиме операции выполняются
последовательно.Возможно для ускорения использовать преимущества конвейризации вычислений
Векторный режим. В этом
режиме операции выполняются аппаратно по специальным векторным командам на группами, состоящими из элементов, максимальное число которых определяется длиной вектора.
Параллельный (скалярный параллельный режим. В этом режиме операция различных итераций одного и того же цикла выполняются параллельно рядом вычислительных элементов (ВЭ).
Векторный параллельный режим. Операции в этом режиме выполняются параллельно несколькими ВЭ над группой из элементов, максимальное число которых определяется длиной вектора.
Слайд 6Возможные режимы расчета массива A(I):
Пусть в цикле, работающим с
этим массивом, производится 8192 арифметические операции с двойной точностью.
Пусть
наш компьютер очень медленный, и длительность такта составляет 170 нс (производительность 0,39 миллионовопераций с плавающей точкой в секунду).
Тогда время выполнения цикла в скалярной режиме составит 0,02 с, и цикл осуществиться за 122472 такта.
Слайд 7Возможные режимы расчета массива A(I):
Скалярный:
Векторный:
122472 такта
241842 такта
24184 такта
В векторном режиме,
если длина вектора будет равна 32, длительность цикла составит 0,0041с
(24184 такта)
Слайд 8Скалярно-параллельный режим
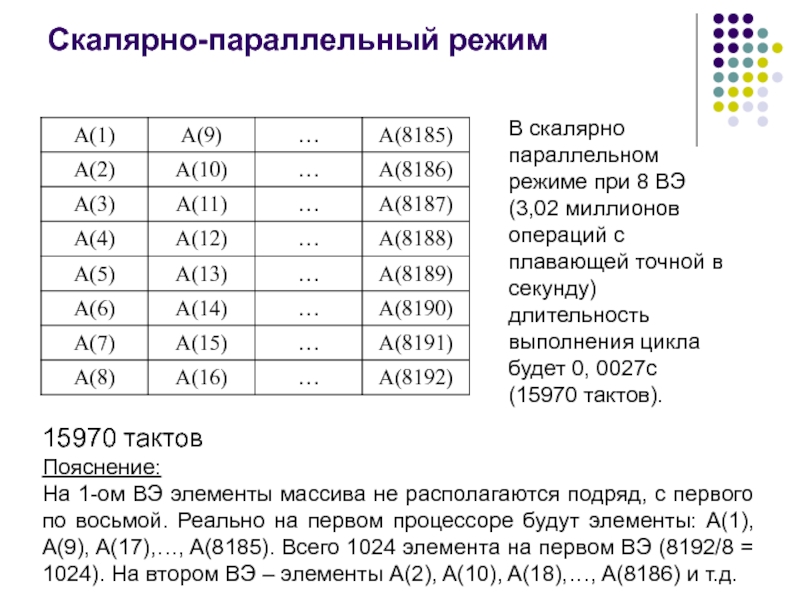
15970 тактов
Пояснение:
На 1-ом ВЭ элементы массива не располагаются подряд,
с первого по восьмой. Реально на первом процессоре будут элементы:
A(1), A(9), A(17),…, A(8185). Всего 1024 элемента на первом ВЭ (8192/8 = 1024). На втором ВЭ – элементы A(2), A(10), A(18),…, A(8186) и т.д.
В скалярно параллельном режиме при 8 ВЭ (3,02 миллионов операций с плавающей точной в секунду) длительность выполнения цикла будет 0, 0027с (15970 тактов).
Слайд 9Векторно – параллельный режим
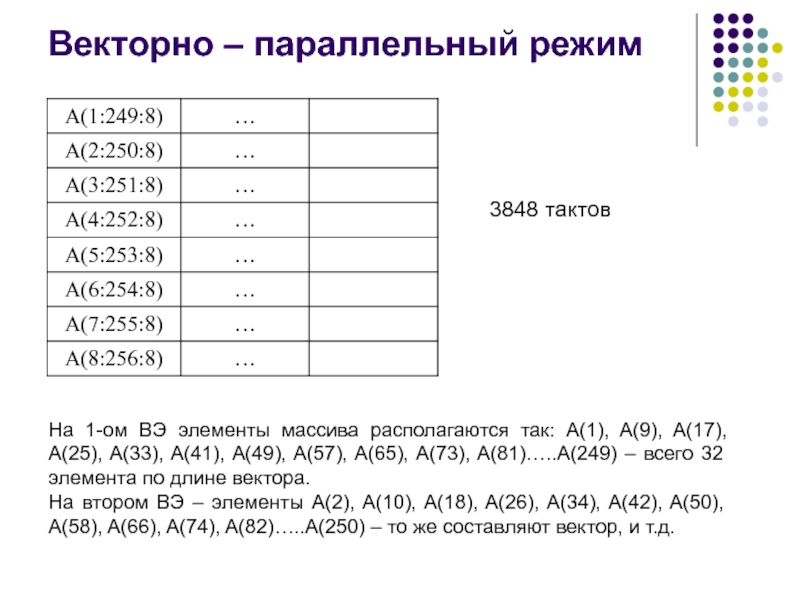
3848 тактов
На 1-ом ВЭ элементы массива располагаются
так: A(1), A(9), A(17), A(25), A(33), A(41), A(49), A(57), A(65),
A(73), A(81)…..А(249) – всего 32 элемента по длине вектора.
На втором ВЭ – элементы A(2), A(10), A(18), A(26), A(34), A(42), A(50), A(58), A(66), A(74), A(82)…..А(250) – то же составляют вектор, и т.д.
Слайд 10Вложенные циклы
В случае вложенных циклов внутренний цикл выполняется в векторном
режиме, а внешний – в параллельном.
Если один цикл вложен
в другой, то говорят, что такая конструкция выполняется в режиме «внешний – параллельно, внутренний - векторно» (ВПВВ).
В следующем примере итерации цикла по J выполняются параллельно, а итерации по I внутри каждого цикла по J – в векторном режиме:
DO 11 J = 1, L
DO 12 I = 1,N
A(I,J) = A(I,J) +S
END DO
END DO
Слайд 11Операция с массивом в цикле. Операции с многомерными массивами
Операция с
массивом в цикле также выполняется в режиме ВПВВ.
При этом
операция с массивом векторизуется, а итерации цикла выполняются параллельно.
Следующая программа эквивалентна программе, представленной выше:
DO J = 1, L
A(1:N,J) = A(1:N,J) +S
END DO
Операции с многомерными массивами также выполняются в режиме ВПВВ.
Цикл по самому левому индексу векторизуется, циклы по следующим индексам реализуются в параллельном режиме.
Следующая программа эквивалентна программе, представленной выше:
A(1:N, 1:J) = A(1:N, 1:J) +S
Слайд 12Ограничения параллелизации циклов
Оптимизация цикла путем выполнения его в параллельном
режиме или посредством векторизации ограничена в следующих случаях:
Не оптимизируется пустой
цикл.
Цикл, реализующийся в векторном, векторно-параллельном режиме или ВПВВ режиме, может содержать только операторы следующих типов:
оператор присваивания
комментарии
CONTINUE
GOTO c передачей управления вперед на метку, содержащуюся в цикле
блок IF, ELSE, END IF
логический оператор IF
Следует отметить, что представленный перечень не содержит операторов ввода-вывода
Слайд 13Ограничения параллелизации циклов
Включение в цикл DO следующих операторов:
ELSE IF
блок IF
с вложенностью, превышающей 3
оператор GO TO с передачей управления вперед
на метку, находящуюся за пределами цикла
RETURN
STOP
запрещает векторизацию, но допускает параллельное выполнение.
Включение символьных переменных в цикл запрещает параллельную реализацию и векторизацию.
Слайд 14Ограничения параллелизации циклов
Использование в цикле ссылок на функции-операторы и встроенные
функции не препятствует оптимизации.
Ссылки в цикле на внешние процедуры
препятствуют оптимизации, если только пользователь явно не разрешает это сделать.
Использование в цикле ссылок на функции-операторы и встроенные функции не препятствует оптимизации.
Ссылки в цикле на внешние процедуры препятствуют оптимизации, если только пользователь явно не разрешает это сделать.
Слайд 15Векторные конструкции
В оптимизируемой программе рассматриваются следующие данные:
Вектор – последовательность
элементов. Вектор может быть образован посредством операций над массивами или
с помощью операций цикла, в которых используются элементы массива.
Например, в следующей программе используется вектор, состоящий из N последовательных элементов массива А:
A(1:N) = A(1:N) +S
или
DO I = 1, N
A(I) = A(I) +S
END DO
Слайд 16Скаляры цикла
Скаляры цикла – это отдельные элементы, используемые в векторной
операции.
Скаляр цикла - ссылка на скалярную переменную или на
отдельный элемент массива. Примеры:
DO I = 1, N
A(I) = A(I) + B(J)+S
END DO
B(J), S – скаляры цикла
Слайд 17Индекс – отдельный целочисленный элемент, значение которого изменяется на постоянное
приращение для каждого элемента вектора.
Целочисленная величина постоянного приращения (ЦПП)
в пределах некоторого цикла определяется следующим образом:
рекуррентная ЦПП – переменная плюс или минус некоторое выражение, инвариантное в пределах цикла
ЦПП, определяемая по предшествующей ЦПП, ранее встречавшаяся в цикле ЦПП, связанная знаком сложения, вычитания или умножения с выражением, инвариантным в пределах этого цикла.
Пример:
DO 16 I = 1, N
J = J+1
K = I*2+3
A(J) = B(K)
CONTINUE
K – ЦПП, поскольку I определено ранее, J – не ЦПП, поскольку ранее не определено
Слайд 18Косвенная адресация
Косвенная адресация реализуется тогда, когда индекс сам является
элементом индексируемого массива. Из-за косвенной адресации снижается эффективность программ. Затраты
времени могут значительно возрасти, если будет делаться попытка выполнения двух операций записи в один и тот же элемент массива.
Замена скалярной переменной
Скалярная переменная, используемая в некотором оптимизируемом цикле вместе с элементами массивов, может быть временно (на время выполнения цикла) заменена на вектор, что позволяет реализовать векторный параллельный режим вычислений
Слайд 19Отказ от оптимизации
В некоторых случаях использование векторизации или распараллеливание
циклов может привести к резкому снижению производительности.
В таких случаях
специальные директивы позволяют отказаться от оптимизации
Слайд 20Отказ от векторизации
Отказ от векторизации может повысить производительность в следующих
ситуациях:
Циклы с небольшим числом итераций. Если число итераций цикла не
превосходит 3-х (длина векторов равна числу итераций), то отказ от векторизации обычно приводит к уменьшению времени выполнения программы
Наличие в цикле условных операторов, используемых для обработки массивов. В таких циклах во время выполнения команд может оказаться мало вычислений.
Слайд 21Отказ от векторизации
Разветвление типа «выбор». Если в каждом цикле выбирается
одна из нескольких возможных ветвей, невозможно эффективно сгруппировать скалярные операции
в целях векторизации
Неравномерно нагруженные итерации. Если в теле цикла число ветвей не велико (как, например, в простом блоке IF … ELSE), а ветвь, в которой используются элементы массива, выбирается очень редко, то от векторизации целесообразно отказаться .
Чтобы быть уверенным в повышении эффективности программы с помощью векторизации, следует измерить время ее выполнения как с векторизацией, так и без нее.
Слайд 22Можно отказаться от распараллеливания циклов, в которых большая часть кода
не может быть оптимизирована вследствие зависимостей данных.
Следует отказаться от
распараллеливания коротких циклов с небольшим числом итераций (однако не менее 5).
При определенных обстоятельствах можно изменить стандартный метод обработки (внешний – параллельно, внутренний – векторно) вложенных циклов.
Отказ от режима параллельной обработки
Слайд 23Зависимость данных
Зависимость данных между итерациями цикла (она также называется рекурсией
данных, или обратной связью по данным) означает, что вычисления в
некоторой итерации цикла зависят от результатов вычислений, полученных на предыдущей итерации, так что должен поддерживаться нужный порядок выполнения операций.
Зависимость данных может оказаться причиной запрета векторизации и распараллеливания цикла.
Слайд 24Рекурсивное использование скалярных переменных
Скалярная переменная, на которую в теле
цикла есть ссылка и значение которой после этого изменяется, называется
рекурсивно используемой скалярной переменной, поскольку ее значение устанавливается в одной итерации цикла и используется в следующей итерации. Например:
S = 0
DO 17 I = 1, N
S = S*A(I) + B(I)
CONTINUE
Слайд 25Исключение рекурсивное используемых скалярных переменных
В определенных ситуациях рекурсивно используемые
скалярные переменные могут быть исключены. Например (не связан с предыдущим!):
T
= 0
DO I = 1, N
S = A(I) + B(I)
C(I) = S +T
T = S
END DO
В этом случае рекурсивно используемая переменная не накапливается и не вычисляет рекурсивно данные, она просто сохраняет результат, вычисленный в предыдущей итерации.
Слайд 26Исключение рекурсивное используемых скалярных переменных
Или (альтернативная запись предыдущего примера):
C(1) =
A(1) * B(1)
DO I = 1, N
C(I) = A(I) *
B(I) + A(I-1) * B(I-1)
END DO
В этом примере в каждой итерации дополнительно выполняется умножение, зато цикл удается полностью оптимизировать.
Несмотря на дополнительную операцию умножения, этот цикл выполняется при полной оптимизации в несколько раз быстрее предыдущего.
Слайд 27Исключение рекурсивное используемых скалярных переменных
Рекурсивные вычисления могут быть заменены явными
не рекурсивными вычислениями, которые не эффективны в скалярном режиме, но
допускают полную оптимизацию.
Пусть матрица:
Храниться в памяти в виде вектора (где отсутствуют повторяющиеся значения, поэтому длина вектора не 16, а 10):
Слайд 28Исключение рекурсивное используемых скалярных переменных
В следующей программе при обращении к
диагональным элементам матрицы A(J) используется рекурсивное определение индекса.
Эта программа
из-за такой рекурсии не может быть векторизована или распараллелена.
J = 0
DO I = 1, N
J = J+I
A(J) = A(J) + B(I) + T
END DO
Однако рекурсивное вычисление может быть заменено явной формулой (формулой для вычисления суммы ряда).
DO I = 1, N
J = (I*I+I)*0.5
A(J) = A(J) + B(I) + T
END DO
Слайд 29Обратные ссылки на элементы массива:
Обратная ссылка на элемент массива
происходит тогда, когда элемент массива определяется во время одной итерации,
а значение его используется в следующей итерации.
Если определение значения и ссылка на тот же элемент массива происходят параллельно, то будет получен результат, отличающийся от того, который был бы получен при последовательных действиях.
(Если распараллеливать итерации цикла, то они могут происходить не синхронно, и, если один ВЭ хочет высчитать новое значение с использованием того, которое должен был вычислить другой ВЭ, а тот еще этого сделать не успел, то будет не понятно что)
Слайд 30Обратные ссылки на элементы массива:
Например:
Часто для достижения того же результата
могут быть использованы не рекурсивные методы, допускающие оптимизацию.
Если в
приведенном выше примере целью является присвоение значения 1.0 каждому элементу сегмента массива А(1:N), то рекурсивная программа может быть заменена простым присваиванием массиву нужного значения:
A(1:N) = 1.0
Слайд 31Обратные ссылки на элементы массива:
Для присваивания нужного значения можно использовать
следующий цикл:
DO I = 1, N
A(J) = 1.0
END DO
Слайд 32Обратные ссылки на элементы массива:
Присваивание одному элементу массива значения другого
элемента массива не обязательно приводят к обратным ссылкам из одной
итерации к другой итерации.
Например, при записи в предыдущий элемент оптимизация допустима:
DO I = 1,N
A(I) = A(I+1)
CONTINUE
где А = (1, 2, 3, 4) (т.е. заранее известны)
A(1) = A(2) = 2
A(2) = A(3) = 3
A(3) = A(4) = 4
При определенном шаге перекрытия нет.
Слайд 33Обратные ссылки на элементы массива:
DO I = 1,N,2
A(I+1) =
A(I)
CONTINUE
где А = (1, 2, 3, 4, 5,6)
A(2) = A(1)
= 1
A(4) = A(3) = 3
A(6) = A(5) = 5
или:
DO I = 1,N,3
A(I+3) = A(I)
CONTINUE
где А = (1, 2, 3, 4, 5,6)
A(4) = A(1) = 1
A(5) = A(2) = 2
A(6) = A(3) = 3
Слайд 34Обратные ссылки на элементы массива:
В некоторых ситуациях обратные ссылки могут
возникать или не возникать во время выполнения программы в зависимости
от значений переменных. Если существует уверенность в том, что обратные ссылки не возникают, то оптимизацию следует разрешить.
Те циклы, которые не оптимизируются или оптимизируются частично, должны быть проанализированы с целью определения возможности преобразования их к виду, допускающему оптимизацию.
Например, следующий цикл не оптимизируется, так как элементы массива А, определенные в одной итерации, используются в следующей итерации.
DO I = 2, N
S(I) = A(I -1) + B(I)
А(I) = А(I) + C(I)
END DO
Слайд 35Обратные ссылки на элементы массива:
Однако те же самые действия можно
выполнить с использованием двух циклов, в которых уже не возникают
обратные ссылки.
DO I = 2, N
А(I) = А(I) + C(I)
END DO
DO 25 I = 1, N
S(I) = A(I -1) + B(I)
CONTINUE
Некоторые циклы, частично оптимизированные для векторно-параллельного режима, выполняются значительно быстрее в скалярно-параллельном режиме.
Слайд 36Повторная запись в элемент массива
Распараллеливание (но не векторизация) запрещается,
если существует возможность записи нескольких значений в один и тот
же элемент массива, поскольку в таком случае должен быть сохранен порядок записи значений.
Такая адресация возможна, если при работе с массивом возможна косвенная адресация.
В нижеследующем примере индекс элемента массива А не может быть определен во время компиляции программы.
DO I = 1, N
A(J(I)) = B(I)
END DO
Однако, если известно, что во время выполнения программы не может произойти повторная запись в какой-либо элемент массива, например известно, что все элементы массива имеют различные значения, то оптимизация возможна.
Слайд 37Синхронизация параллельных операций
Потенциально работа в векторно-параллельном и скалярно-параллельном режимах
при последовательной записи значений в массивы может приводить к искажению
результатов записи.
Предположим, например, что выполняется следующий цикл:
DO I = 1,N
A(I) = A(I+1)
END DO
Если нулевой вычислительный элемент ВЭ0 выполняет пересылку A(32) = A(33) в то время, как ВЭ1 выполняет пересылку A(33) = A(34), то прежде чем ВЭ1 изменит значение A(34), ВЭ0 должен произвести запись значения A(32) в A(33). Необходимо произвести соответствующую синхронизацию.
Слайд 38Условное присваивание значений скалярным и индексным переменным
Если в цикле есть
скалярная переменная, значение которой изменяется в условном операторе и используется
затем в том же цикле, то она является рекурсивно используемой скалярной переменной.
Такие циклы оптимизировать запрещено.
В следующем цикле значение скалярной переменной S изменяется в условном операторе и затем используется в следующем операторе присваивания, что препятствует оптимизации.
DO I = 1,N
IF (A(I).GT.X) S = B(I) +2
A(I) = S
CONTINUE
Слайд 39Условное присваивание значений скалярным и индексным переменным
Если изменение скалярной переменной
и ее последующее использование производится в одном условном операторе, то
цикл, содержащий такой оператор, оптимизируется.
Например:
DO I = 1,N
IF (A(I).GT.X) THEN
S = B(I) +2
A(I) = S
END IF
CONTINUE
Слайд 40Параллельные независимые подпрограммы
Цикл DO может использоваться для выполнения отдельных
подпрограмм или независимых вызовов подпрограмм параллельно, если каждый отдельный вызов
подпрограммы осуществлять по условию в определенной итерации цикла.
Если одна подпрограмма вызывается повторно, гарантировано, что она рекурсивна.
Слайд 41Внешние процедуры
По умолчанию векторизуемые или распараллеливаемые циклы не могут содержать
вызовы внешних процедур, поскольку в таких случаях нельзя произвести проверку
зависимости данных.
Слайд 42Предостережения
Необходимо уделять большое внимание обработке нелокальных данных в подпрограммах, вызываемых
в параллельном цикле, поскольку такая параллельная программа будет выполняться асинхронно
на нескольких процессорах.
В частности, нельзя обращаться к одному и тому же элементу данных в памяти класса COMMON или EQUIVALENCE при «наложении» аргументов, т.е. при передаче одного и того же элементы данных двум различным формальным параметрам, если только этот элемент данных не определяется в подпрограмме.
Слайд 43Предостережения
Т.е. если, например, в цикле вызывается подпрограмма, внутри которой определяется
глобальная переменная, а цикл распараллеливается, то на разных ВЭ при
работе с подпрограммой будут вычисляться различные значения глобальной переменной, и этот процесс необходимо будет синхронизировать.
Программист должен быть уверен в том, что подпрограмма не вводит в программу не обнаруживаемой зависимости данных.
Во избежание этой опасности рекомендуется использовать чистые функции. (В чистой функции никакие аргументы не определяются: определяется лишь возвращаемое значение).