Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРИЗМА
Содержание
- 1. ПРИЗМА
- 2. ОглавлениеОпределениеЭлементы призмыСвойства призмыВиды призмПризмы в сооружениях
- 3. ОпределениеПризма -многогранник, две грани которогоявляются конгруэнтными многоугольниками,
- 4. Элементы призмыОснования - две грани, являющиеся конгруэнтными
- 5. Диагональное сечение - пересечение призмы и диагональной
- 6. Свойства призмыОснования призмы являются равными многоугольниками.Боковые грани
- 7. Виды призмПрямая призма - это призма, у
- 8. Правильная призма - это призма в основании
- 9. Слайд 9
- 10. Скачать презентанцию
ОглавлениеОпределениеЭлементы призмыСвойства призмыВиды призмПризмы в сооружениях
Слайды и текст этой презентации
Слайд 3Определение
Призма -многогранник, две грани которого
являются конгруэнтными многоугольниками,
лежащими в параллельных
плоскостях, а остальные
этими многоугольниками.Слайд 4Элементы призмы
Основания - две грани, являющиеся конгруэнтными многоугольниками, лежащими в
параллельных плоскостях (ABCDE, KLMNP).
Боковые грани - все грани, кроме оснований.
Каждая боковая грань обязательно является параллелограммом (ABLK, BCML, CDNM, DEPN, EAKP).Боковая поверхность - объединение боковых граней.
Полная поверхность - объединение оснований и боковой поверхности.
Боковые ребра - общие стороны боковых граней (AK, BL, CM, DN, EP).
Высота - отрезок, соединяющий основания призмы и перпендикулярный им (KR).
Диагональ - отрезок, соединяющий две вершины призмы, не принадлежащие одной грани (BP).
Диагональная плоскость - плоскость, проходящая через боковое ребро призмы и диагональ основания.
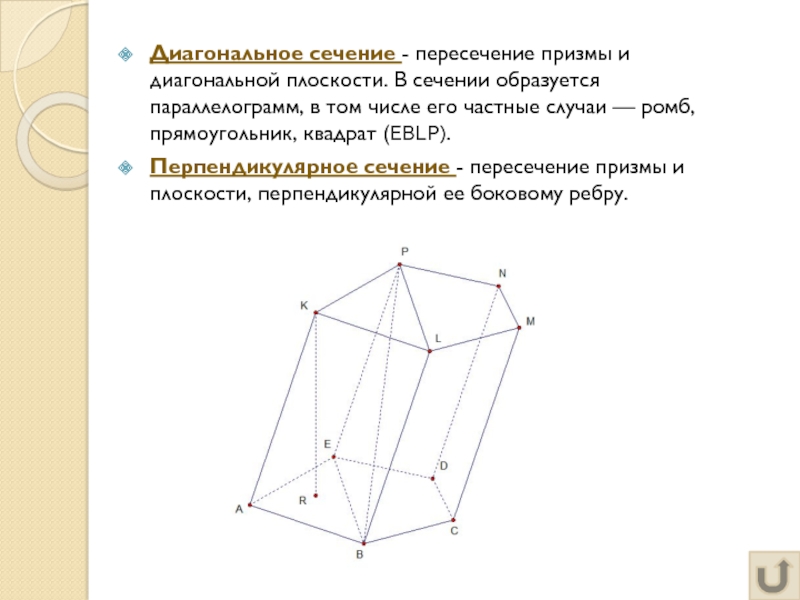
Слайд 5Диагональное сечение - пересечение призмы и диагональной плоскости. В сечении
образуется параллелограмм, в том числе его частные случаи — ромб,
прямоугольник, квадрат (EBLP).Перпендикулярное сечение - пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Слайд 6Свойства призмы
Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые
ребра призмы параллельны и равны.
Объём призмы равен произведению её высоты
на площадь основания: V = S ∙ h
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Площадь боковой поверхности произвольной призмы S = P ∙ l , где P - периметр перпендикулярного сечения, l - длина бокового ребра.
Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Слайд 7Виды призм
Прямая призма - это призма, у которой все боковые
ребра
перпендикулярны основанию, в противном
случае призма называется наклонной.
Площадь боковой
поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или высоту).В прямой призме боковые ребра являются высотами.
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
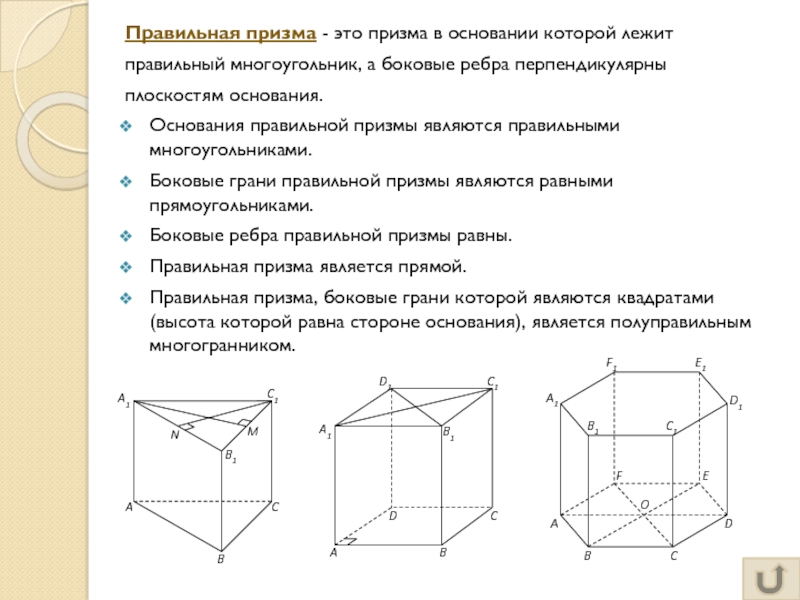
Слайд 8Правильная призма - это призма в основании которой лежит
правильный многоугольник,
а боковые ребра перпендикулярны
плоскостям основания.
Основания правильной призмы являются правильными
многоугольниками.Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.