Признаки равенства Прямоугольных треугольников

=
B1
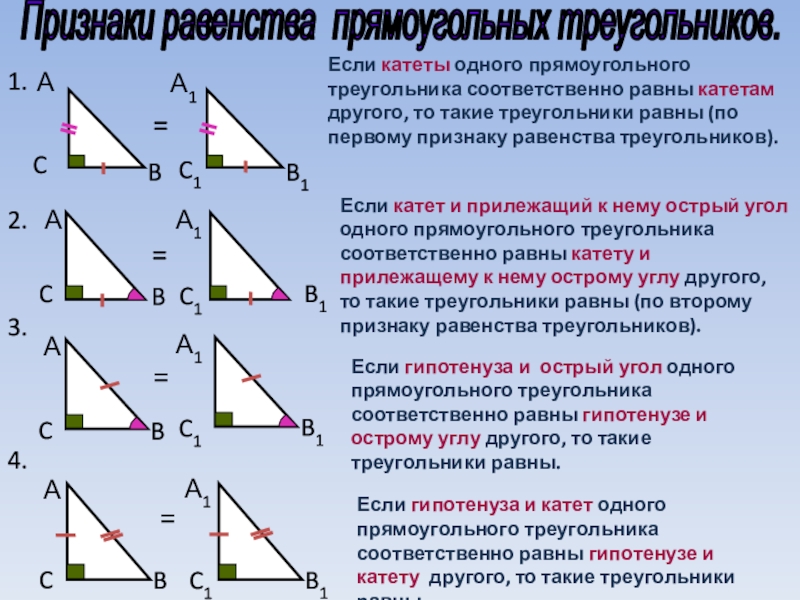
Если катеты одного прямоугольного треугольника соответственно равны катетам другого,

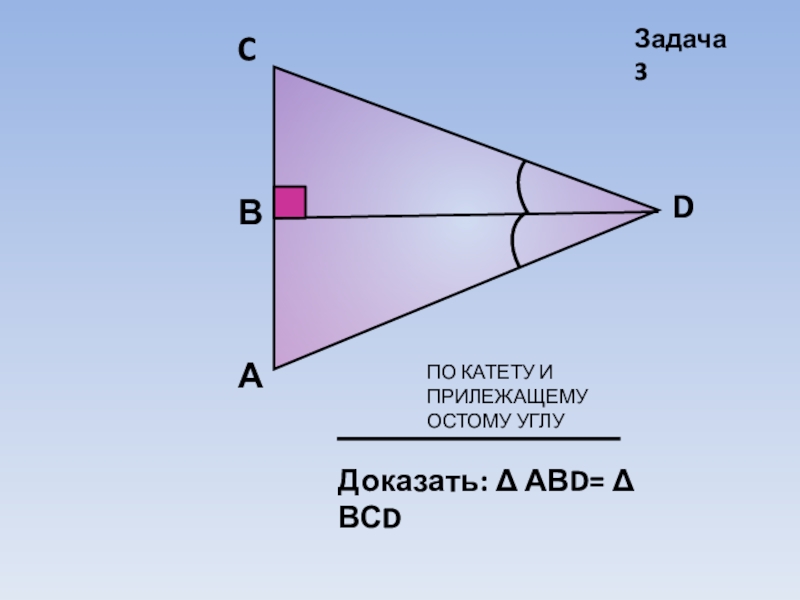
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны (по второму признаку равенства треугольников).

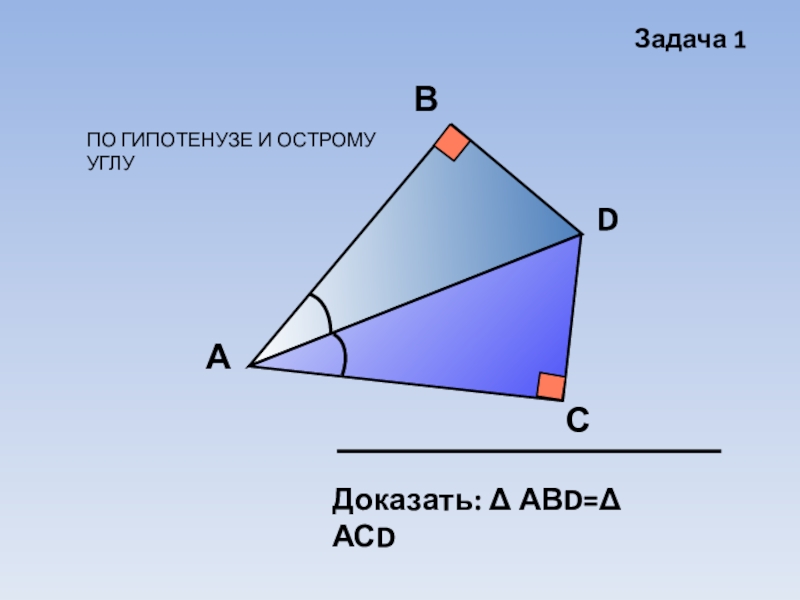
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

А

C

B

А1

C1

B1

4.

3.

А1

C1

B1

=

=

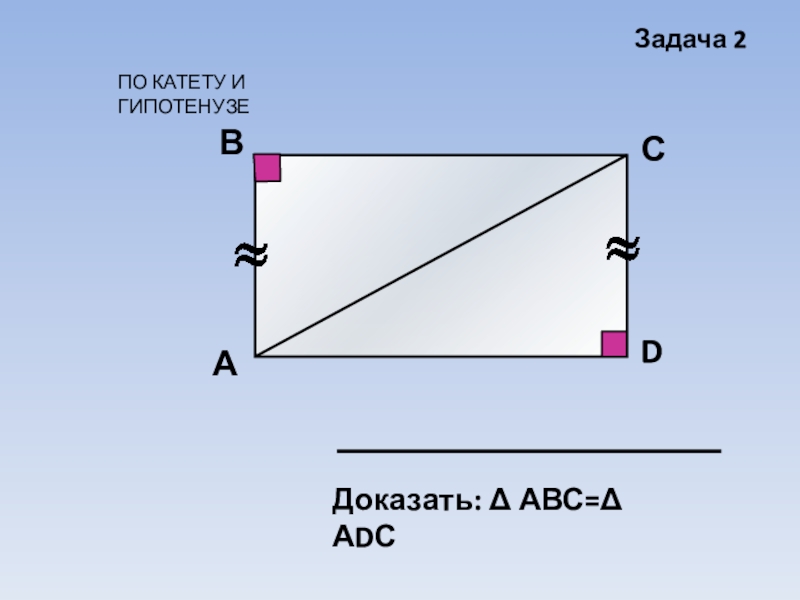
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

УГЛУ

∆АВD = ∆ BDC
Дано: ∆MNK,
NQ – высота, MN = NK
Доказать:

2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р

Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A

1 вариант

2 вариант

1.

2.

= DC
Доказать: ∆АВD = ∆ BDC
Доказательство: АD = DC по

Дано: ∆MNK,
NQ – высота, MN = NK
Доказать: ∆MNQ = ∆ NKQ

2. Дано: ∆PKM-прямоугольный,
PMN = 150
Найти: Р

Дано: ∆АВС-прямоугольный,
СВD = 120
Найти: A

∆АВD = ∆ BDC по
катетам.

1.

1.

2.

1 вариант

2 вариант

Доказательство:MN= NK по условию, NQ – общий катет.

∆MNQ = ∆ NKQ по гипотенузе и катету.

PMN = 180°-150 = 30°, как смежные углы.

Р = 90° - 30° = 60°, как сумма острых углов прямоугольного треугольника.
Ответ: 60°

Решение:

Решение:

АВС = 180°-120 = 60°,
как смежные углы.

А = 90° - 60° = 30°, как сумма острых углов прямоугольного треугольника.
Ответ: 30°