Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проекционно-сеточные методы решения уравнений математической физики
Содержание
- 1. Проекционно-сеточные методы решения уравнений математической физики
- 2. 08/13/2019Цель курса: Освоение методологии вычислительного эксперимента на
- 3. 08/13/2019Литература Калиткин Н.Н. Численные методы. – М:
- 4. 08/13/2019Введение: система – средство достижения цели человекомВ
- 5. 08/13/2019Введение: Задачи анализа и синтезаДля достижения своих
- 6. 08/13/2019Примеры технических системДвижение планет и космических объектовДинамика
- 7. 08/13/2019Тема 1 Математические модели и численные
- 8. 08/13/2019Как исследуются физические явления и решаются задачиИмеется
- 9. 08/13/2019Математическая модель - это описание исследуемого объекта
- 10. 08/13/2019Пример: Модель конденсатора+-Простейшая модельНе учитывает краевых эффектовБолее сложная модельС учетом краевых искажений поля
- 11. 08/13/2019Методы (алгоритмы) решения математических задачРешить задачу -
- 12. 08/13/2019Как оценивается погрешность вычислений?Погрешность обычно оценивают одним
- 13. 08/13/2019Нормированное пространство Множество элементов в котором каждому
- 14. 08/13/2019Пространство непрерывных функций С[ab]Множество непрерывных функций {f(x),
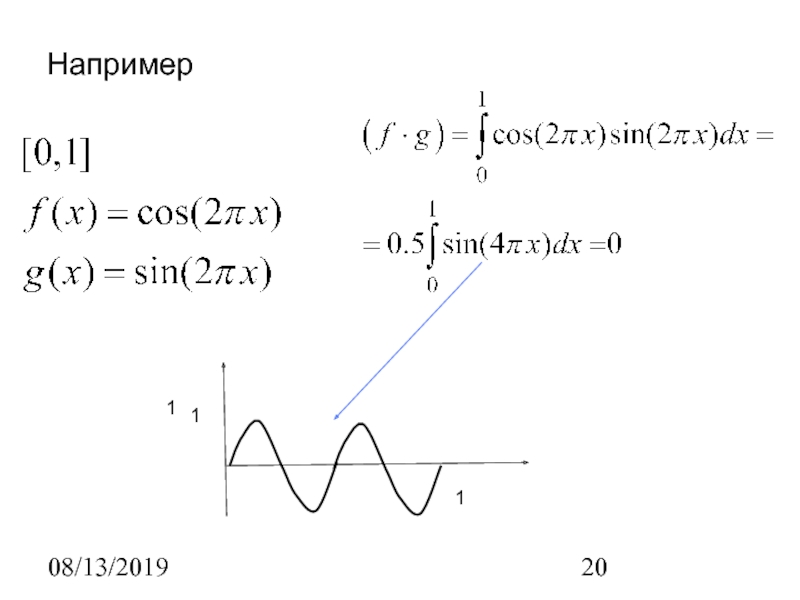
- 15. 08/13/2019Например11
- 16. 08/13/2019Пространство Лебега L2[a, b] интегрируемых
- 17. 08/13/2019Например11
- 18. 08/13/2019Заметим, что функции f и g на
- 19. 08/13/2019Скалярное произведение в L2[a,b] Ортогональными называются две функции из L2, если (f, g)=0.
- 20. 08/13/2019Например111
- 21. 08/13/2019Пространство Соболева Множество функций, имеющих интегрируемые с
- 22. 08/13/2019Виды погрешностейАбсолютная погрешность ΔX между точным X
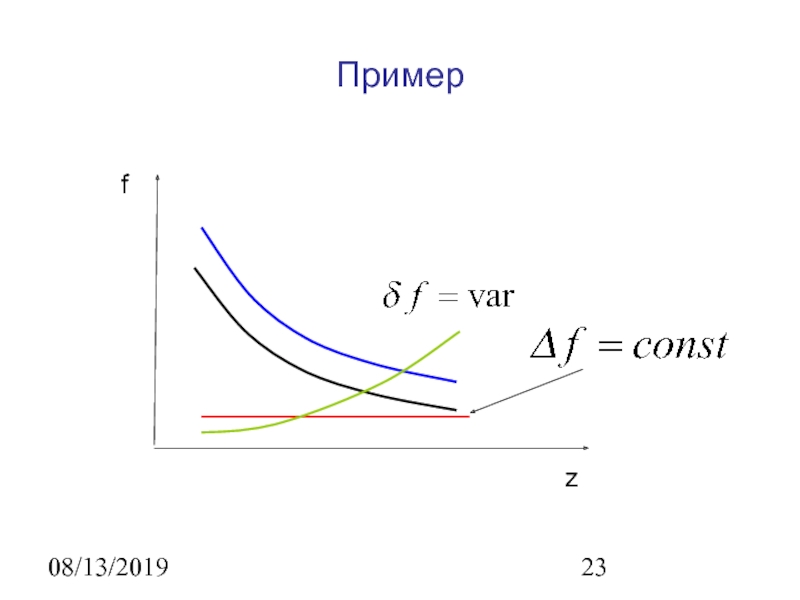
- 23. 08/13/2019Примерzf
- 24. 08/13/2019Откуда возникают погрешности расчетов? Есть четыре источника
- 25. 08/13/2019Неточность математической моделиЛюбая модель является определенной идеализацией
- 26. 08/13/2019Погрешность исходных данныхИсходные данные обычно получаются из
- 27. 08/13/2019Погрешность методаПри построении вычислительного алгоритма обычно точное
- 28. 08/13/2019Например, метод вычисления y=e-x при x>0 Метод – несколько первых членов рядаПогрешность:
- 29. 08/13/2019Ошибки округленийВсе расчеты на ЭВМ производятся с
- 30. 08/13/2019Итерационные методы решения задач Задача: Итерационные методы
- 31. 08/13/2019Процесс вычисленийЗадают начальное приближение и по формуле
- 32. 08/13/2019Пример простого итерационного методаПриводим уравнение к видуМожно
- 33. 08/13/2019Конец темы 1Задавайте Ваши вопросы
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 108/13/2019
Курс Основы информационных технологий
Раздел
Проекционно-сеточные методы решения уравнений математической физики
Професcор
Синицын
412 – 5к)Слайд 208/13/2019
Цель курса: Освоение методологии вычислительного эксперимента на базе моделей сплошной
среды, используемых для поддержки принятия решений при проектировании технических систем
Слайд 308/13/2019
Литература
Калиткин Н.Н. Численные методы. – М: Наука, 1978.
Болсун
А.И., Гронский В.К., Бейда А.А. Методы математической физики. – Мн.:
Выш. Шк., 1988.Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. – М.: Наука, 1981.
Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь, 1988.
Марчук Г.И. Методы вычислительной математики. – М.: - Наука, 1980.
Синицын А.К. Современные информационные технологии. Проекционно-сеточные методы решения уравнений математической физики. Конспект лекций для аспирантов и магистрантов Мн.: БГУИР, 2004.
Синицын А.К. ,Навроцкий А.А. Алгоритмы вычислительной математики. Учебно-методическое пособие. Мн.: БГУИР, 2007
Слайд 408/13/2019
Введение: система – средство достижения цели человеком
В качестве средства достижения
цели человек создает (или приспосабливает имеющуюся) некую
систему – т.е.
набор связанных элементов, образующих целостный объект. Например, машина, телевизор, система производства, система нагрева, экономическая, общественная, мировоззренческая,…
Первые системы – рука-палка, колесо-телега, катапульта,..
Чтобы создать нужную систему он должен:
Предугадывать результаты действий системы.
Придумывать, как она должна быть устроена.
Слайд 508/13/2019
Введение: Задачи анализа и синтеза
Для достижения своих целей, в частности
при создании полезных систем, человеку приходится постоянно решать две задачи
–Экспертную и конструктивную.
Э.З. ставится следующим образом - «Что будет, если…». Как ведет себя система(объект) в тех или иных условиях?
Это задача анализа.
К.З. ставится следующим образом – «Как сделать, чтобы…». Как сконструировать систему (объект) с заданными свойствами?
Это задача синтеза.
Слайд 608/13/2019
Примеры технических систем
Движение планет и космических объектов
Динамика атмосферы и океана
Техника
генерации, усиления, передачи и приема электромагнитных волн
Элементы компьютерной техники- элементы
памяти, записи, преобразования сигналовТехнологические установки выращивания кристаллов с заданными свойствами
Установки сушки, термообработки и охлаждения материалов
Устройства автоматического управления
Все эти и многие другие системы объединяет то, что они описываются дифференциальными уравнениями.
Поэтому, чтобы их спроектировать, необходимо решить ДУ и найти оптимальные условия работы.
Большая доля современных пакетов программ и систем программирования для этого предназначена.
Слайд 708/13/2019
Тема 1 Математические модели и численные методы
Как исследуются
физические явления и решаются задачи
Как оценивается погрешность вычислений?
Откуда
возникают погрешности расчетов? Итерационные методы решения задач
Слайд 808/13/2019
Как исследуются физические явления и решаются задачи
Имеется два способа решения
инженерных и физических задач:
экспериментальный и теоретический.
Экспериментальный метод, как правило,
связан с большими материальными затратами, а иногда в принципе невозможен.Теоретический метод, или математическое моделирование, опирается на знание фундаментальных законов природы, используя которые строят математическую модель исследуемой системы.
Слайд 908/13/2019
Математическая модель - это описание исследуемого объекта (системы) с помощью
математических символов и операций над ними
Требования к модели:
Адекватность. - В
модели реализуется отображение существенных свойств объекта при его изучении.Экономичность. Бритва Оккама- отбрасываются незначительные факторы.
Принцип дополнительности. Использовать несколько моделей по возможности.
Математическая постановка задачи -предполагает описание математической модели и указание цели ее исследования.
найти max f(x);
найти x, при котором f(x)=0, и др.
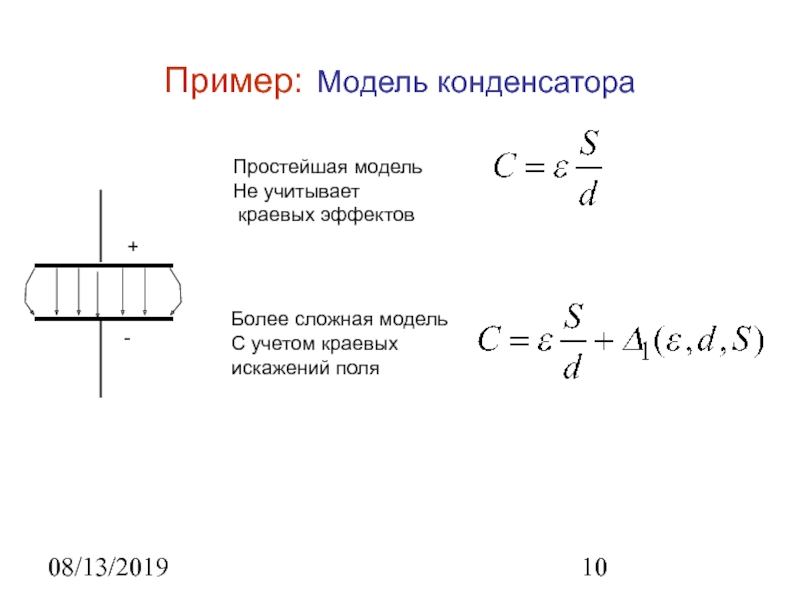
Слайд 1008/13/2019
Пример: Модель конденсатора
+
-
Простейшая модель
Не учитывает
краевых эффектов
Более сложная модель
С учетом
краевых
искажений поля
Слайд 1108/13/2019
Методы (алгоритмы) решения математических задач
Решить задачу - это значит указать
алгоритм (т.е. строгую последовательность действий) для получения требуемого результата из
исходных данныхК точным методам относятся алгоритмы, позволяющие за конечное число действий получить в принципе (если нет ошибок округления) точное решение. Обычно оно получается в виде формулы или конечного вычислительного алгоритма.
Приближенные - это методы, позволяющие за счет некоторых допущений свести решение исходной задачи к задаче, имеющей точное решение.
Численные методы предполагают разработку вычислительного алгоритма, т.е. конечной, строгой последовательности арифметических и логических действий, обеспечивающих получение решения с заданной контролируемой погрешностью.
Слайд 1208/13/2019
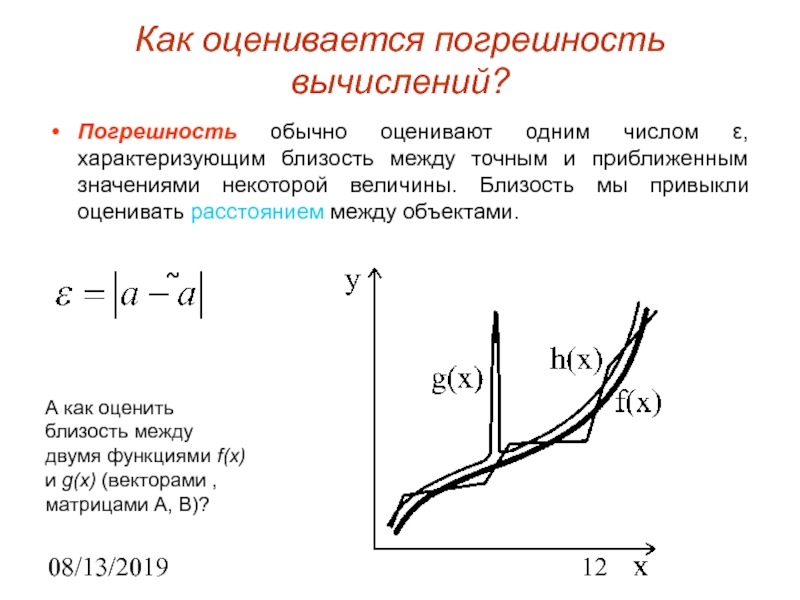
Как оценивается погрешность вычислений?
Погрешность обычно оценивают одним числом ε, характеризующим
близость между точным и приближенным значениями некоторой величины. Близость мы
привыкли оценивать расстоянием между объектами.А как оценить близость между двумя функциями f(x) и g(x) (векторами , матрицами A, B)?
Слайд 1308/13/2019
Нормированное пространство
Множество элементов в котором каждому элементу поставлено в
соответствие число ║X║ (норма X), удовлетворяющее следующим аксиомам:
1.
- норма (положительное число).2. только при X = ∅ (∅- нулевой элемент).
3. , α - число
4. - неравенство треугольника.
В качестве элементов рассматриваются функции, векторы или матрицы.
Введены обычные операции + - и умножение * на число α
Расстояние между элементами
Слайд 1408/13/2019
Пространство непрерывных функций С[ab]
Множество непрерывных функций {f(x), g(x), h(x), …},
определенных на интервале [a, b].
Норма и расстояние в C[a, b]
определяются по формулам:
Слайд 1608/13/2019
Пространство Лебега L2[a, b]
интегрируемых с квадратом функций
Множество функций,
для которых
В L2[a, b] имеются и разрывные функции,
т.е. C[a, b]⊆ L2[a, b].Норма и расстояние:
Слайд 1808/13/2019
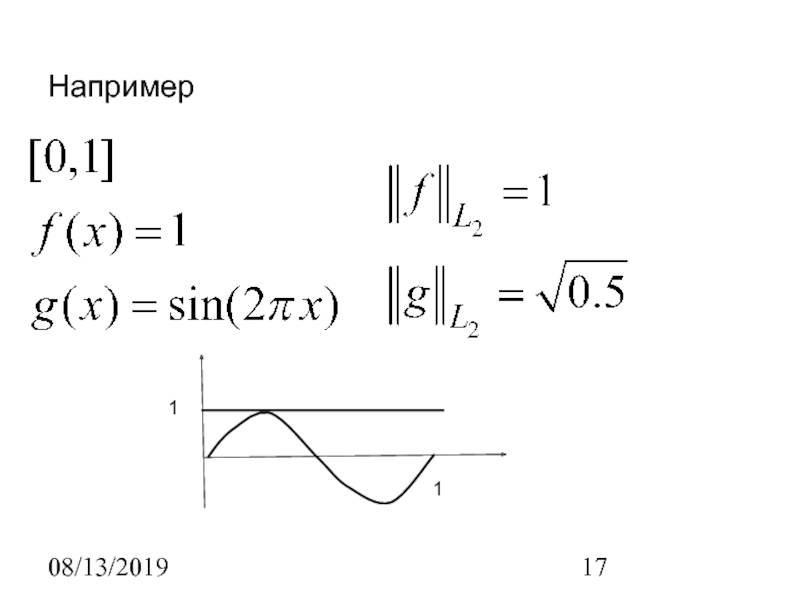
Заметим, что функции f и g на рис.
будут "близкими" в
пространстве L2
и "далекими" в пространстве С,
т.е. норма С
более «сильная»:Слайд 1908/13/2019
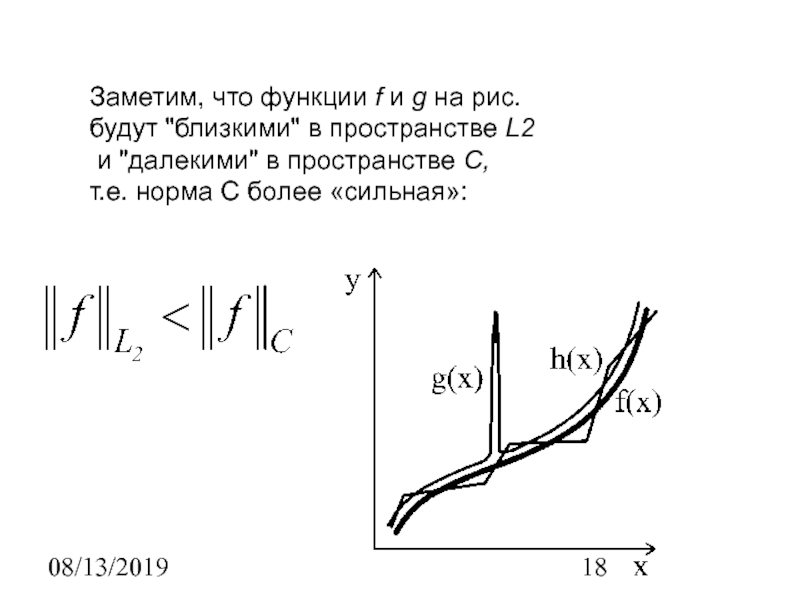
Скалярное произведение в L2[a,b]
Ортогональными называются две функции из L2,
если (f, g)=0.
Слайд 2108/13/2019
Пространство Соболева
Множество функций, имеющих интегрируемые с квадратом производные до
s порядка.
Норма определяется как
Расстояние
В этом пространстве близость
между функциями характеризует также близость их производных.Функции f и h на рис. 1.1 будут «близкими» по норме и «далекими» по норме , причем
Слайд 2208/13/2019
Виды погрешностей
Абсолютная погрешность ΔX между точным X и приближенным
значениями некоторого элемента определяется через норму разности
Относительная
погрешность δX определяется как отношение абсолютной погрешности к норме элемента
Слайд 2408/13/2019
Откуда возникают погрешности расчетов?
Есть четыре источника погрешности результата, о
которых следует помнить при выполнении расчетов
1. Неточность математической модели
2.
Погрешность исходных данных 3. Погрешность метода
4. Ошибки округлений
Слайд 2508/13/2019
Неточность математической модели
Любая модель является определенной идеализацией рассматриваемого физического явления
и описывает лишь основные факторы, существенные при решении конкретной технической
задачи.Уточнение модели за счет введения описания дополнительных факторов обычно приводит к ее усложнению и, как следствие, к трудности использования, поэтому необходим определенный компромисс (Бритва Оккама).
Выбор удачного компромисса - это творческий процесс, требующий большого опыта и инженерной интуиции.
Слайд 2608/13/2019
Погрешность исходных данных
Исходные данные обычно получаются из измерений либо -
наоборот, по этим данным затем делается устройство. В каждом случае
имеется так называемая неустранимая погрешность между исходными данными, участвующими в расчетах, и теми, которые реализуются. В результате этого получаемое решение также будет отличаться от реализуемого в устройстве.В зависимости от того, как ошибки исходных данных отражаются на результате, задачи разделяют на два класса: корректные и некорректные.
Задача называется корректной, если малые ошибки исходных данных приводят к пропорционально малым ошибкам решения.
Задача называется некорректной, если малые ошибки исходных данных приводят к большим ошибкам в результатах,.
Для решения некорректных, но правильных с физической точки зрения задач разрабатываются специальные методы
Слайд 2708/13/2019
Погрешность метода
При построении вычислительного алгоритма обычно точное решение представляется в
виде бесконечного предела последовательности арифметических и логических действий.
При ограничении
лишь конечным числом вычислений вносится погрешность, контролируемая некоторыми параметрами метода.Получение зависимости погрешности решения от параметров вычислительного метода является одной из основных задач вычислительной математики
Обычно при уменьшении некоторого параметра h метода погрешность решения εh стремится к нулю, т.е. при . . В этом случае, если выполняется оценка , где С - const и не зависит от h, считается, что порядок погрешности равен p и обозначается коротко
Слайд 2808/13/2019
Например, метод вычисления y=e-x при x>0
Метод – несколько первых
членов ряда
Погрешность:
Слайд 2908/13/2019
Ошибки округлений
Все расчеты на ЭВМ производятся с конечным числом значащих
цифр, определяемым объемом ячеек памяти. Поэтому при вычислении, например, 1/3
= 0,3333...3..., и если округление производится на седьмом знаке, то вносится ошибка ε ≈ 10-8.Когда вычислений много, то такие ошибки могут накапливаться и, наоборот, компенсироваться (положительные и отрицательные).
В зависимости от реакции на погрешность округлений вычислительные методы разделяются на устойчивые и неустойчивые.
Метод устойчив, если в процессе вычислений ошибки округлений не накапливаются, в противном случае метод неустойчив.
При увеличении количества вычислений по неустойчивому методу ошибки быстро нарастают, что приводит к переполнению ЭВМ.
Одной из задач вычислительной математики является установление условий устойчивости и разработка рекомендаций по созданию устойчивых методов.
Слайд 3008/13/2019
Итерационные методы решения задач
Задача:
Итерационные методы основаны на построении
сходящейся к точному решению x* бесконечной рекуррентной последовательности
элементов той же природы, что и x*.Последовательность называется рекуррентной порядка m, если каждый следующий ее член выражается через m предыдущих по некоторому правилу
Для реализации m-шагового метода требуется задать m первых членов, называемых начальным приближением
Слайд 3108/13/2019
Процесс вычислений
Задают начальное приближение и по формуле xm=ϕ(xm-1) последовательно находят
Процесс получения следующего k-го члена через предыдущие называется k-й итерацией.
Итерации выполняются до тех пор, пока очередной член xk не будет удовлетворять заданной точности, т.е.
Ввиду того, что точное решение x* заранее неизвестно, обычно сходимость метода определяют по близости двух последних членов, т.е. расчеты производят до тех пор, пока не выполнится условие или более точно
Получаем x*≅xk
Слайд 3208/13/2019
Пример простого итерационного метода
Приводим уравнение к виду
Можно так
Рекуррентная последовательность
Задаем начальное
условие x0 и находим x1, x2, … xk
Условие сходимости











![Проекционно-сеточные методы решения уравнений математической физики 08/13/2019Пространство непрерывных функций С[ab]Множество непрерывных функций {f(x), g(x), h(x), …}, определенных 08/13/2019Пространство непрерывных функций С[ab]Множество непрерывных функций {f(x), g(x), h(x), …}, определенных на интервале [a, b].Норма и расстояние](/img/thumbs/853fb9ae4c799165db49c5a731192fb8-800x.jpg)
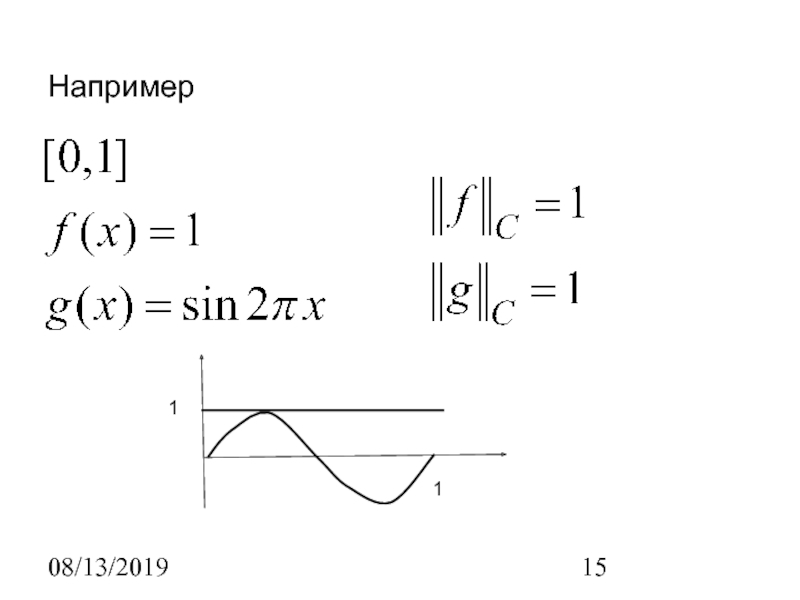
![Проекционно-сеточные методы решения уравнений математической физики 08/13/2019Пространство Лебега L2[a, b] интегрируемых с квадратом функцийМножество функций, для 08/13/2019Пространство Лебега L2[a, b] интегрируемых с квадратом функцийМножество функций, для которых В L2[a, b] имеются](/img/thumbs/4733157acceb7f38eb1582486ee2bc23-800x.jpg)
![Проекционно-сеточные методы решения уравнений математической физики 08/13/2019Скалярное произведение в L2[a,b] Ортогональными называются две функции из L2, если (f, g)=0. 08/13/2019Скалярное произведение в L2[a,b] Ортогональными называются две функции из L2, если (f, g)=0.](/img/thumbs/2f646324a65d9119c3b9bc30f8a2bc20-800x.jpg)