Слайд 1Введение в теорию графов
Область дискретной математики, предметом исследования
которой являются структуры, состоящие из точек (вершин графа) и линий,
соединяющих их произвольным образом со стрелками (дуг графа) либо линий без стрелок (ребер графа).
Теория графов позволяет построить модели для решения задач экономической и планово-производственной практики, включая календарное планирование, сетевое планирование и управление, выбор оптимальных маршрутов и потоков в сетях.
Слайд 2
Дуги - это ориентированные ребра.
Две вершины
могут быть соединены несколькими ребрами или дугами, идущими в одном
направлении.
Эти дуги (ребра) называют кратными (параллельными), а граф с кратными дугами (ребрами) – мультиграф.
Мультимножество – неупорядоченная совокупность элементов, в которой могут быть одинаковые элементы.
Граф задается множеством V и мультимножеством Е, элементом которого являются пары элементов множества V.
Слайд 3
Граф можно описать моделью G = (X,V),
где X –
непустое конечное множество вершин, а V – бинарное отношение на
нем (множество ребер и дуг – отображение X в себя,
V = FX, X = {x1, x2, …, xn}
V = { v1, v2, …, vn }
x2
x1 v1 v3
v2 x4
x3 v4
Слайд 4
Дуга обозначается (xi, xj, v), где xi, xj, и
v – начало дуги, конец и номер. Если дуга (ребро)
единственная, то можно обозначать ее без v (без номера).
Ребра, имеющие общую вершину называют смежными. Соединенные ребром (дугой) вершины – смежными вершинами.
Ребро (дуга) инцидентна вершинам xi и xj, если она их соединяет.
Вершина без дуг – изолированная.
Слайд 5
Граф неориентированный – если каждое его ребро неориентированно.
Граф ориентированный –
если все его ребра ориентированны.
Иначе – смешанный граф.
Граф из одних
изолированных вершин –
нуль граф.
Граф простой, если не содержит петель и параллельных дуг (ребер).
Граф полный, если он простой и каждая пара вершин смежна.
Полный ориентированный граф – это турнир.
Слайд 6
Граф G’ = (X’,V’), называется частью графа
G = (X,V),
(G’ ⊂ G), если Х’ ⊂ Х, а V’ ⊂
V, т. е. множество вершин Х’ графа G’ содержится в множестве вершин Х графа G и все ребра (дуги) V’ графа G’ являются ребрами (дугами) V графа G. В случае, если Х’= Х, граф называется суграфом.
Пусть А – некоторое подмножество множества вершин Х графа G. Подграфом G (А) графа G называется такая часть графа, множеством вершин которой является А, а ребрами – все ребра из V, оба конца которых лежат в А. При А=Х, подграф совпадает с G.
Слайд 7
В неориентированном (ориентированном) графе последовательность u1,u2, …,un из n ребер
(дуг), соединяющих вершины Х1 и Хn+1, называется маршрутом или цепью
длиной n, если два соседних ребра (дуги) vi и vj имеют общую концевую точку, т. е.
v1= (x1, x2), v2= (x2, x3), …, un = (хn, хn+1).
Открытая цепь называется путем (см. х6 рисунок), если все ее вершины х4 различны.
х2
Х1 х3 х5
Слайд 8
Одни и те же вершины и ребра в любом маршруте
могут встречаться несколько раз, поэтому внутренняя вершина может оказаться начальной
или конечной вершиной маршрута.
Маршрут называется открытым, если его начальная и конечная вершины различны.
Маршрут замкнут, если х1 = хn+1. Одно ребро может быть маршрутом единичной длины.
Слайд 9
Если все ребра (дуги), составляющие маршрут (ориентированный маршрут) различны, то
такой маршрут (ориентированный маршрут) называется простой цепью (простым путем).
Простая цепь,
где все вершины различны, называется элементарной.
Замкнутая цепь называется циклом (см. рисунок), если различны все ее вершины, за исключением концевых.
Граф называется связным, если каждая пара вершин может быть соединена цепью.
Максимальный связный подграф называется его компонентой связности. х3
х1
х2 х4
Слайд 10
Множество ребер, исключение которых из графа увеличивает число его компонент,
называется разрезом графа.
Связный граф называется деревом (см. рисунок), если он
не имеет циклов. Любой граф, не содержащий циклов, называется лесом, компонентами являются деревья, число ребер в дереве на 1 меньше числа его вершин.
Дерево с выделенной вершиной (корнем), называется деревом с корнем. Х5
Х1 х3
х4
х2 х6
Слайд 11
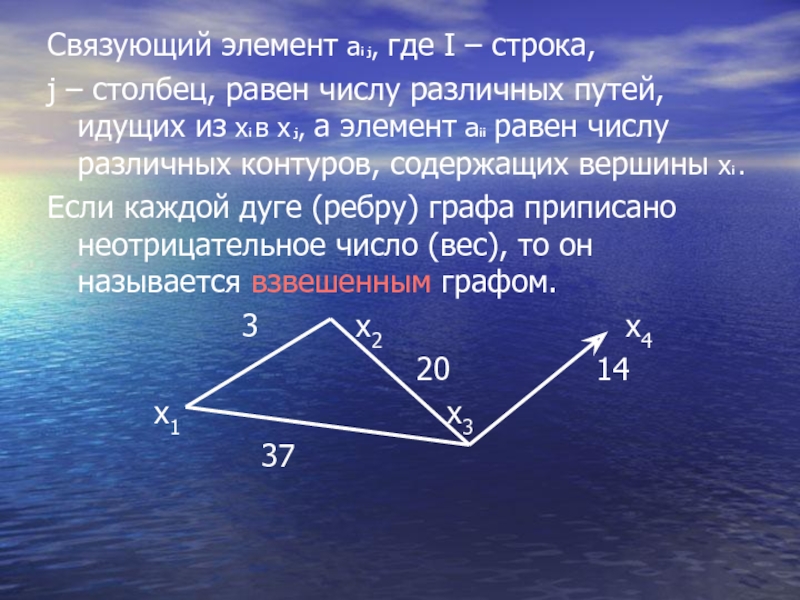
Связующий элемент аi j, где I – строка,
j –
столбец, равен числу различных путей, идущих из хi в х
j, а элемент аii равен числу различных контуров, содержащих вершины хi .
Если каждой дуге (ребру) графа приписано неотрицательное число (вес), то он называется взвешенным графом.
3 х2 х4
20 14
х1 х3
37
Слайд 12
Содержательно все ребра могут означать стоимость передачи информации между узлами,
соответствующими его концам, ее пропускную способность и т. д.
Взвешенные графы
применяются для решения различных транспортных задач, в них часто используют понятие разреза графа.
Задание графа описанием его составляющих V и Е не всегда является оптимальным для решения на компьютере задач о его свойствах, поэтому графы часто представлены матрицами.
Слайд 13
Матрица графа
х1 х2 х3 х4
х1
1 3 3 0
А = 3 0 2 1
3 2 0 1 х3
0 1 1 0 х2
Элемент аi j, где i – строка, а х4
J – столбец, равен числу различных путей, идущих из хi в хj (например элемент а23 = 2, так как из х2 в х3 идут 2 пути.).
Слайд 14
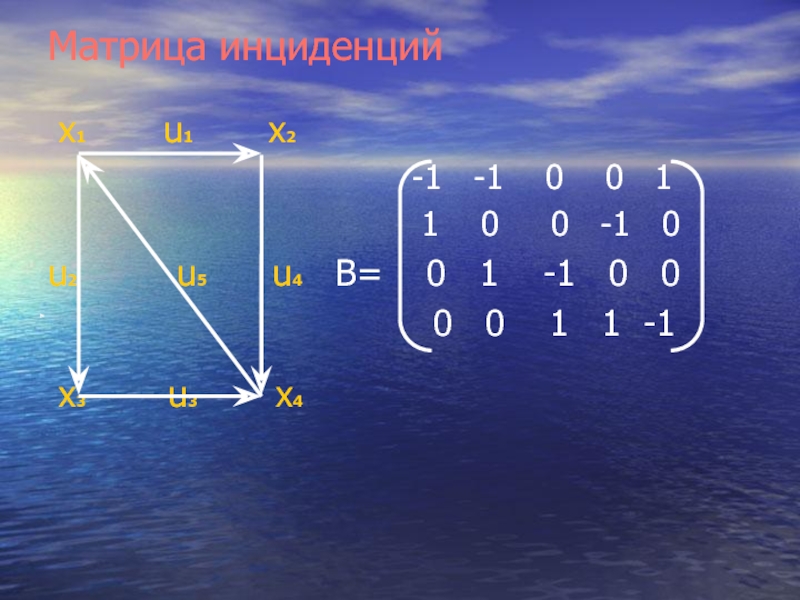
Матрицей инциденций (n x m) В = || bi j
|| для неориентированного графа с n вершинами и m ребрами
называется матрица, строки которой соответствуют вершинам, а столбцы – ребрам. Элемент bi j = 1, если вершина xi инцидентна ребру, иначе bi j = 0.
Слайд 15Матрица инциденций
x1
u1 х2
-1 -1 0 0 1
1 0 0 -1 0
u2 u5 u4 B= 0 1 -1 0 0
0 0 1 1 -1
х3 u3 х4
Слайд 16
Матрица смежности. Граф с n вершинами задается булевой квадратной (n,
n) матрицей, в которой элемент пересечения I строки и J
столбца равен 1, если существует пара (xi, xj) (иначе этот элемент равен 0). Степень вершины xi равна сумме элементов I строки.
Слайд 17
Матрица смежности.
х1 х2
х3
0 1
0 х1
С = 1 0 1
0 1 0
х2
х3
Есть еще и матрицы циклов, матрицы разрезов, матрицы нулей и др. формы матричного представления графов.
Слайд 18
Для ориентированного графа элемент bi j = 1, если
вершина инцидентна дуге и является начальной вершиной дуги (дуга исходит
из нее), и b I j = 1, если дуга входит в вершину.
Если вершина не инцидентна дуге, то элемент
bi j = 0.
Неориентированный граф без петель называется полным, если каждая его вершина смежна со всеми остальными вершинами, полный граф с n вершинами имеет n(n – 1)/2 ребер.
Если множество вершин графа можно разбить на 2 подмножества, все вершины каждого из которых не являются смежными, то граф называется двудольным, в двудольном графе каждое ребро соединяет вершины из разных подмножеств.
Слайд 19
Сети. Обозначим FX i множество вершин, в которое можно перейти
из вершины xi, a F-1X i – множество вершин, из
которых можно попасть в вершину xi.
Ориентированный связный граф с конечным числом вершин без циклов, имеющий одну и только одну вершину х0, для которой F-1X i = Ø, а также одну и только одну вершину Z, для которой Fz = Ø, называется сетью, выделенные вершины в нем называются полюсами.
Вершина х0 - есть вход сети, а вершина Z – выход сети.
Слайд 20
Задачи, решаемые с использованием графов:
Найти кратчайший путь на графе (с
каждым ребром связано конкретное значение) и тогда следует минимизировать сумму
дуг между конкретными вершинами а и в.
Найти критический путь на графе (т. е. самый длинный путь). В реальных задачах планирования – это гарантированный максимальный срок выполнения проекта.
Исследование потоков на сетях.
Дерево решений.