Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проектирование комбинационных схем
Содержание
- 1. Проектирование комбинационных схем
- 2. Цели и задачиПрименение ранее изученных знаний:булева алгебра,логические
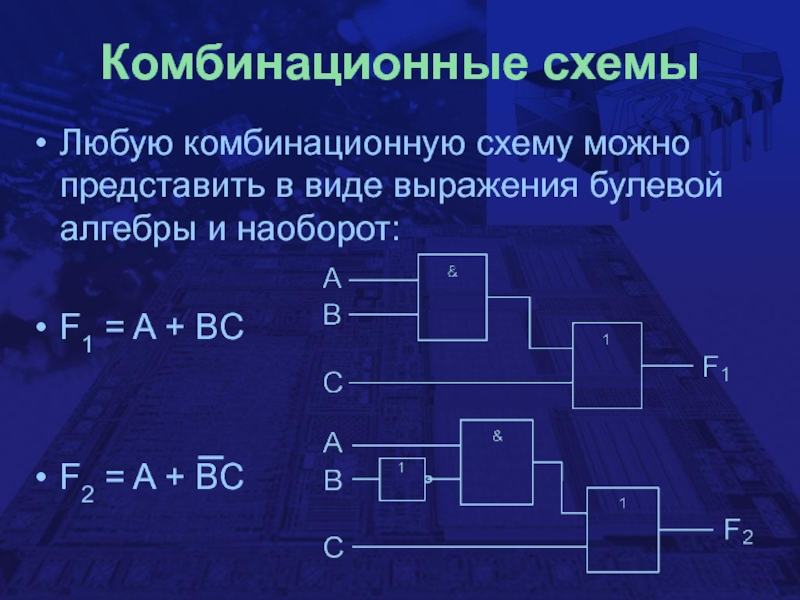
- 3. Комбинационные схемыЛюбую комбинационную схему можно представить в
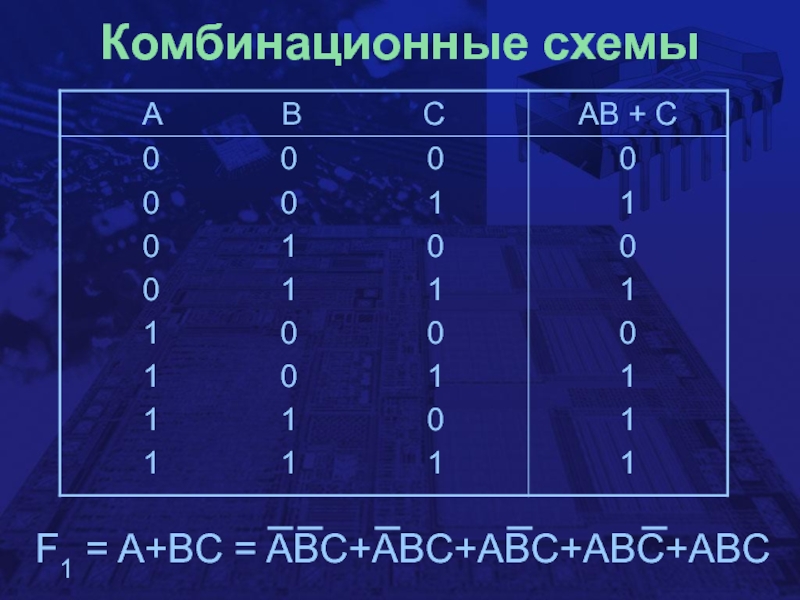
- 4. Комбинационные схемыF1 = A+BC = ABC+ABC+ABC+ABC+ABC
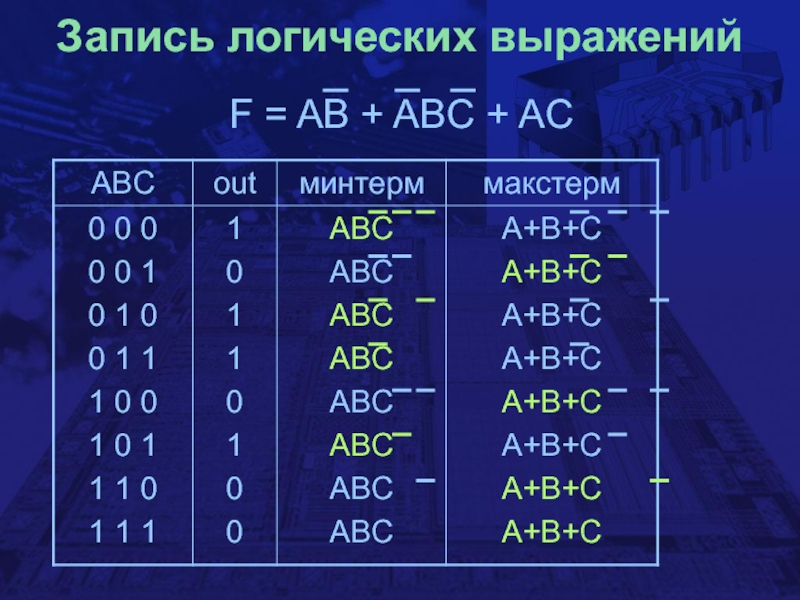
- 5. Запись логических выраженийF = AB + ABC + AC
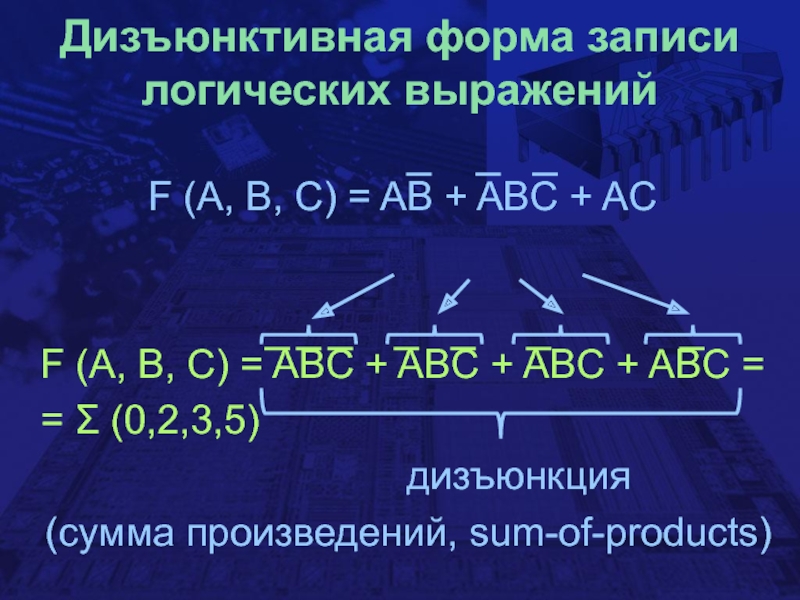
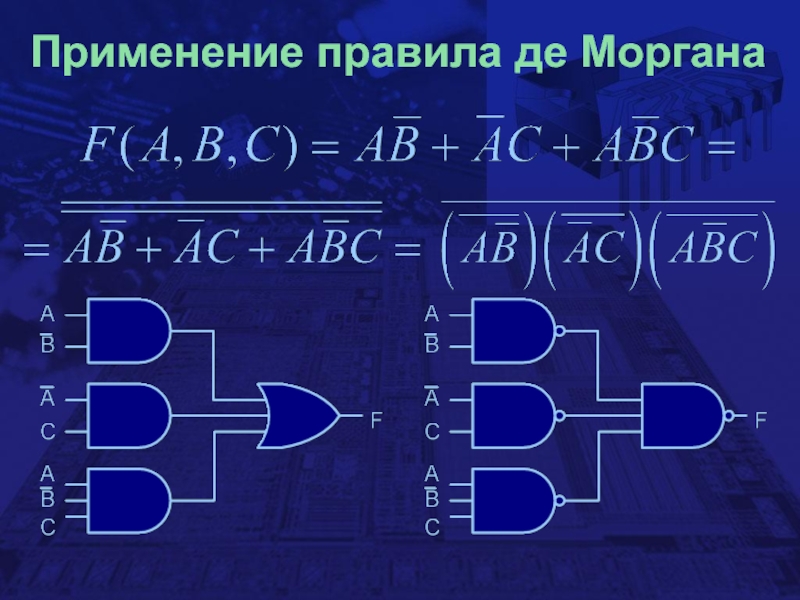
- 6. Дизъюнктивная форма записи логических выраженийF (A, B,
- 7. Дизъюнктивная форма записи логических выраженийДизъюнктивная нормальная форма
- 8. Дизъюнктивная форма записи логических выраженийF (A, B,
- 9. Конъюнктивная форма записи логических выраженийКонъюнктивная нормальная форма
- 10. Пример перехода от ДНФ к СДНФ
- 11. Применение правила де Моргана
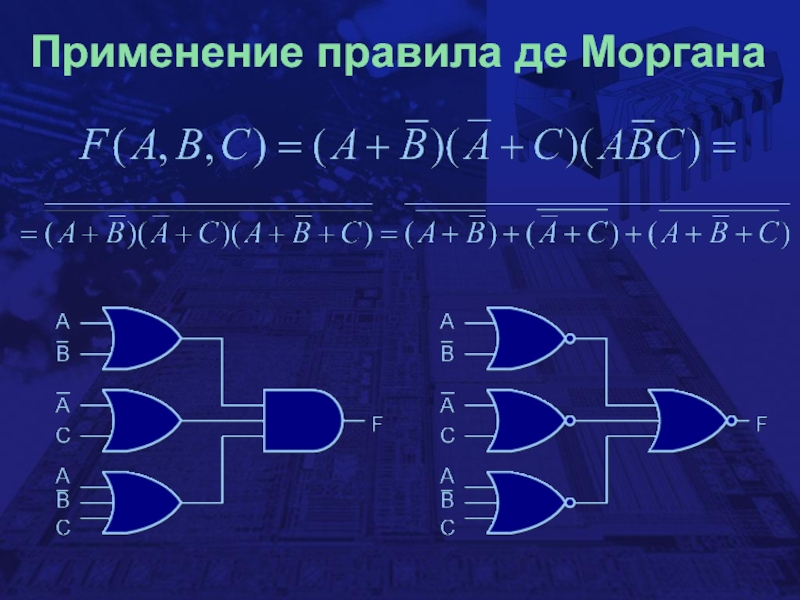
- 12. Применение правила де Моргана
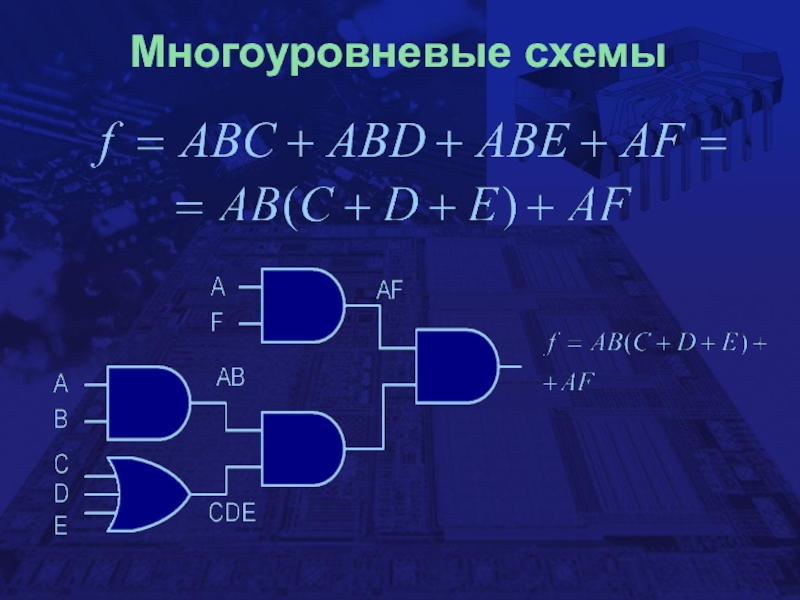
- 13. Многоуровневые схемы
- 14. Алгебраическое упрощение булевых выражений Группировка членов с
- 15. Группировка членовЗакон ассоциативности.Сокращение выражений за счет использования
- 16. Группировка членов
- 17. Приведение в СДНФ или СКНФУмножение на множители
- 18. Приведение в СДНФ или СКНФ
- 19. Использование теоремы де Моргана
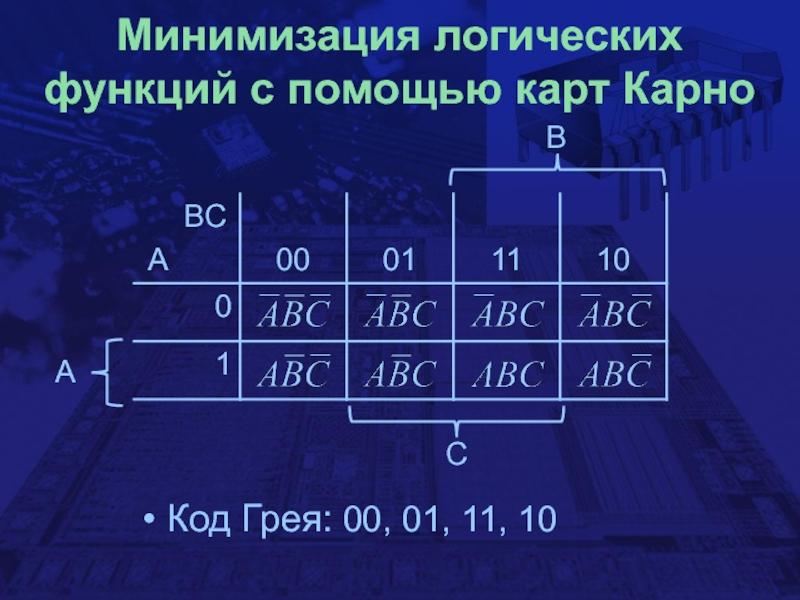
- 20. Минимизация логических функций с помощью карт КарноBCAКод Грея: 00, 01, 11, 10
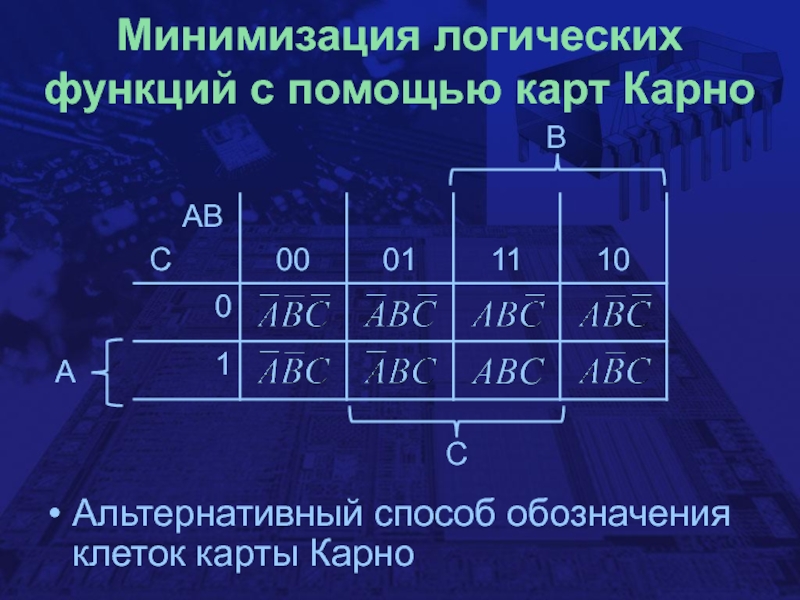
- 21. Минимизация логических функций с помощью карт КарноBCAАльтернативный способ обозначения клеток карты Карно
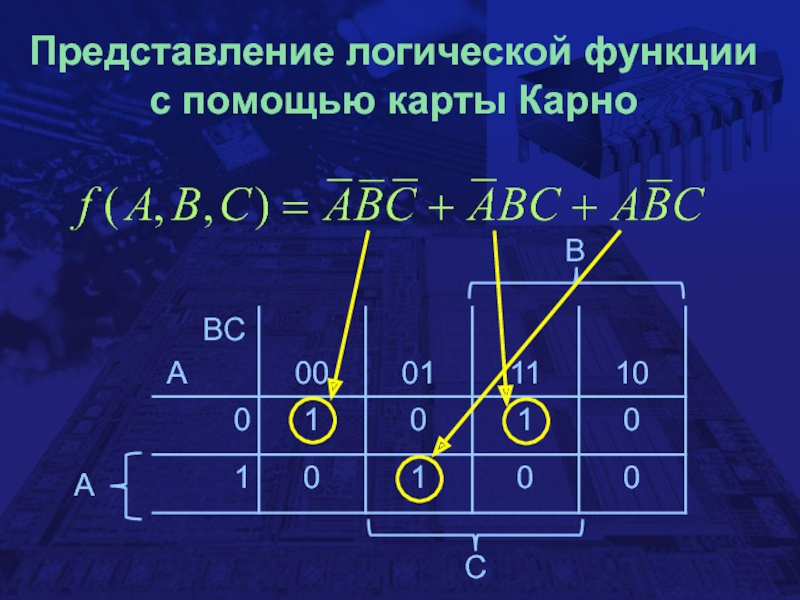
- 22. Представление логической функции с помощью карты КарноBCA
- 23. Алгоритм минимизации логических функций с помощью карт
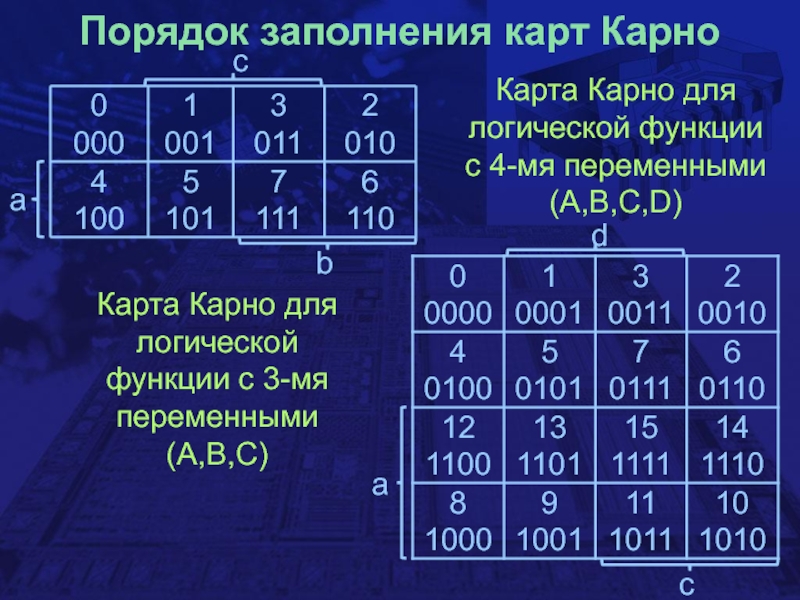
- 24. Порядок заполнения карт КарноКарта Карно для логической
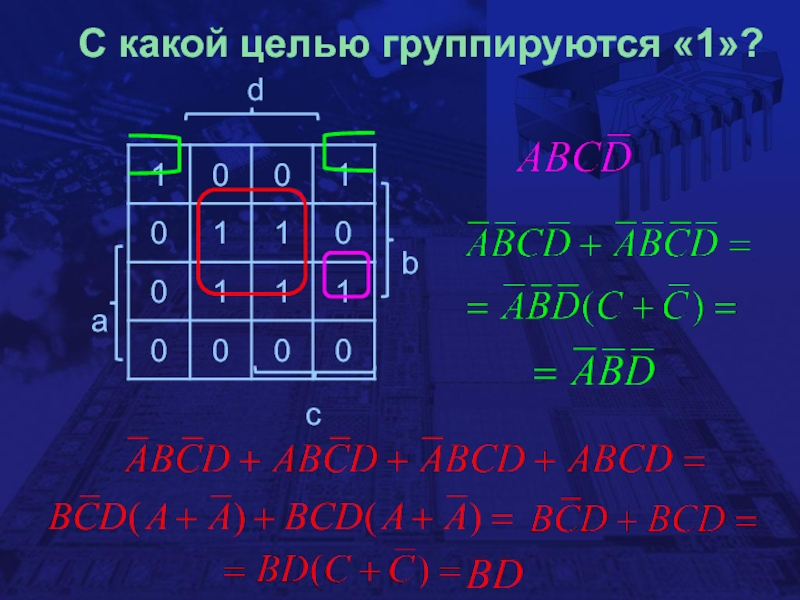
- 25. С какой целью группируются «1»?
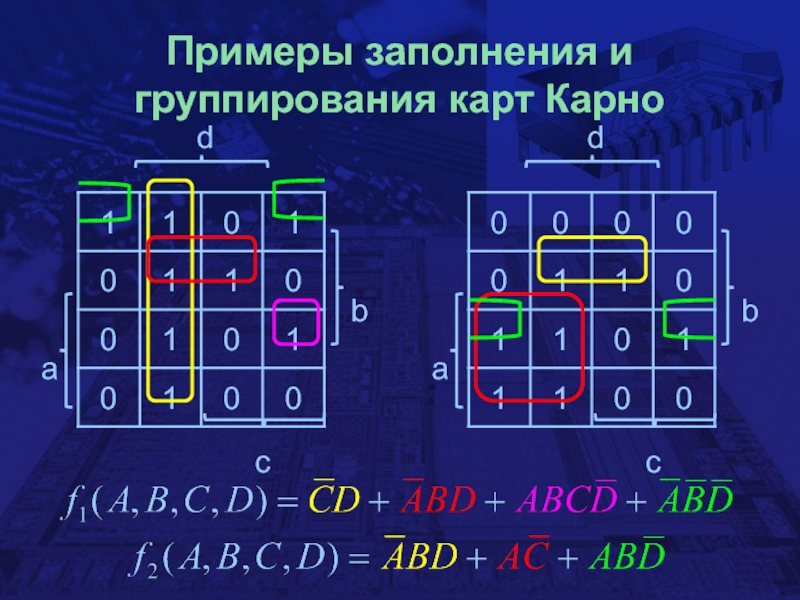
- 26. Примеры заполнения и группирования карт Карно
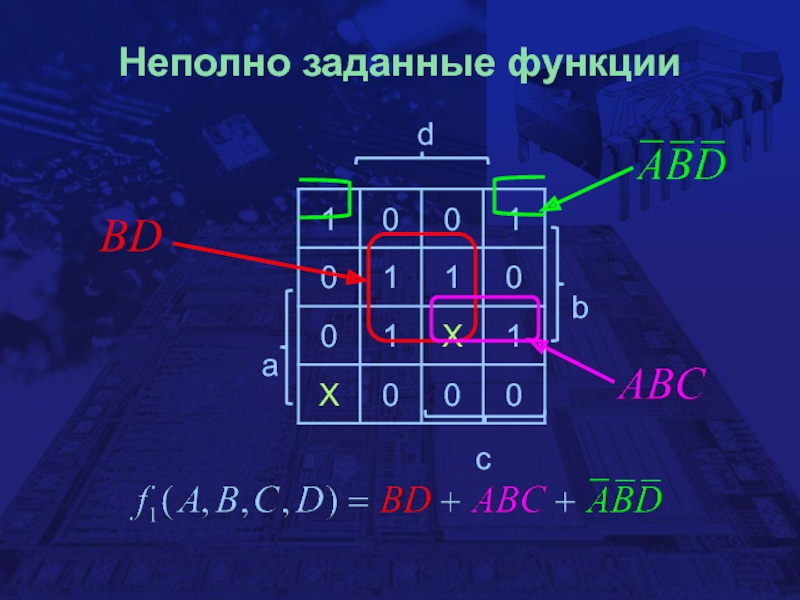
- 27. Неполно заданные функции
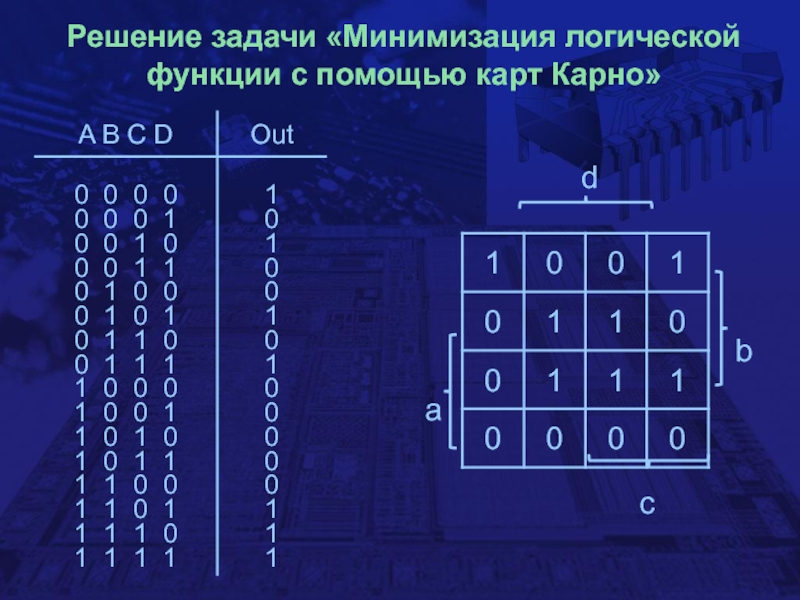
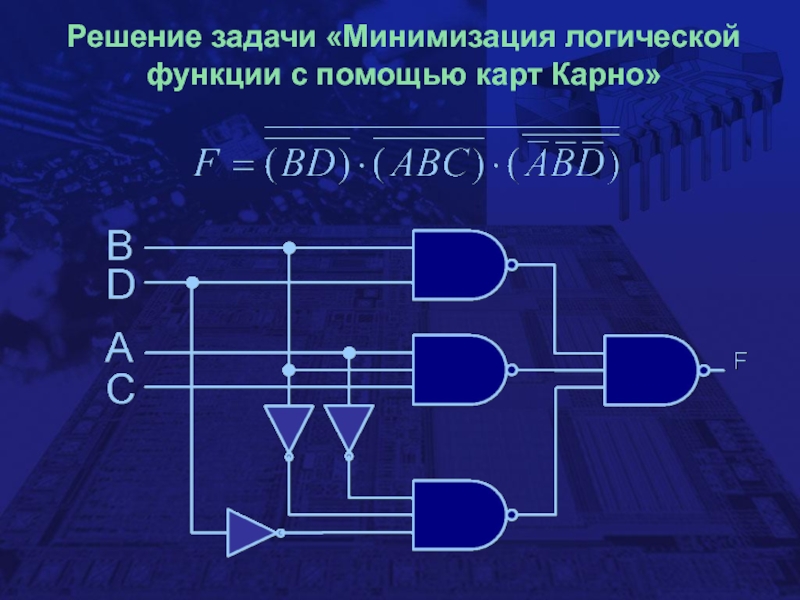
- 28. Решение задачи «Минимизация логической функции с помощью карт Карно»
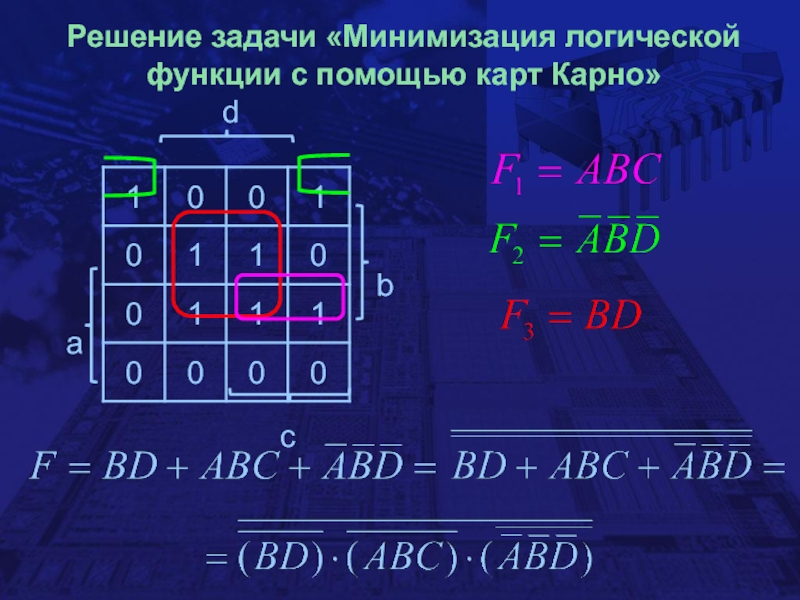
- 29. Решение задачи «Минимизация логической функции с помощью карт Карно»
- 30. Решение задачи «Минимизация логической функции с помощью карт Карно»
- 31. Итоги:В ходе лекции изучены:Представление логических функций в
- 32. Скачать презентанцию
Цели и задачиПрименение ранее изученных знаний:булева алгебра,логические вентили для проектирования несложных комбинационных схем.Минимизация (упрощение) комбинационных схем с помощью упрощения логических выражений и карт Карно
Слайды и текст этой презентации
Слайд 2Цели и задачи
Применение ранее изученных знаний:
булева алгебра,
логические вентили
для
проектирования несложных комбинационных схем.
логических выражений и карт Карно
Слайд 3Комбинационные схемы
Любую комбинационную схему можно представить в виде выражения булевой
алгебры и наоборот:
F1 = A + BC
F2 = A +
BC
Слайд 6Дизъюнктивная форма записи логических выражений
F (A, B, C) = AB
+ ABC + AC
F (A, B, C) = ABC + ABC + ABC + ABC =
= Σ (0,2,3,5)
дизъюнкция
(сумма произведений, sum-of-products)
Слайд 7Дизъюнктивная форма записи логических выражений
Дизъюнктивная нормальная форма (ДНФ):
F (A,
B, C) = AB + ABC + AC
Совершенная дизъюнктивная
нормальная
форма (СДНФ):F (A, B, C) = ABC + ABC + ABC + ABC
Слайд 8Дизъюнктивная форма записи логических выражений
F (A, B, C) = (A+B+C)(A+B)(A+C)
F (A, B, C) = макстермы
= (A+B+C)(A+B+C)(A+B+C)
== П (2,5,6) конъюнкция
(произведение сумм, product-of-sums)
Слайд 9Конъюнктивная форма записи логических выражений
Конъюнктивная нормальная форма (КНФ):
F (A,
B, C) = (A+B+C)(A+B)(A+C)
Совершенная конъюнктивная нормальная форма (СКНФ):
F (A,B,C) =
(A+B+C)(A+B+C)(A+B+C) 
Слайд 14Алгебраическое упрощение булевых выражений
Группировка членов с последующим применением тождеств
Приведение
выражения в каноническую форму с последующим упрощением
Использование теоремы де Моргана
Слайд 15Группировка членов
Закон ассоциативности.
Сокращение выражений за счет использования тождеств.
Один член можно
использовать для группирования несколько раз.
Теорема о непротиворечивости (Consensus Theorem):
Слайд 17Приведение в СДНФ или СКНФ
Умножение на множители типа
Перегруппировка с целью
получения упрощенного выражения
Для упрощения выражений в конъюнктивной форме необходимо преобразовать
по теореме де Моргана, получить инверсную дизъюнктивную функцию – упростить ее по известным правилам.
Слайд 21Минимизация логических функций с помощью карт Карно
B
C
A
Альтернативный способ обозначения клеток
карты Карно
Слайд 23Алгоритм минимизации логических функций с помощью карт Карно
Заполнить карту Карно.
Объединить
все рядом лежащие «1»-цы в группы (кубы) наибольшего размера. Размер
куба может быть только 2n, где n=0,1,2,3….Записать все новые минтермы, соответ-ствующие выделенным группам (кубам).
Записать минимизированную функцию равную логической сумме полученных минтермов.
Слайд 24Порядок заполнения карт Карно
Карта Карно для логической функции с 3-мя
переменными (A,B,C)
Карта Карно для логической функции с 4-мя переменными (A,B,C,D)
Слайд 31Итоги:
В ходе лекции изучены:
Представление логических функций в виде:
выражений булевой алгебры
логических
схем
карт Карно
Упрощение булевых выражений
с использованием алгебраических методов
с использованием карт Карно
