Слайд 1Проектирование реакционного узла для жидкофазных реакторов
Слайд 2Математические модели изотермических реакторов
Обозначения:
V – объём жидкости в реакторе: л,м3;
q
– объёмный расход реакционной массы: л,м3;
co, co – концентрация компонента
на входе в реактор, моль/л;
c – концентрация на выходе из реактора, моль/л;
τ – время пребывания (заполнения) реактора;
t – время;
L (l) – длина реактора;
r, r(c) – скорость химической реакции;
w – линейная скорость.
Слайд 3Пусть в реакторе протекает одна химическая реакция:
А + ……. →
….. продукты
c – концентрация компонента А исходного сырья.
1. Модель реактора
периодического действия:
Слайд 42. Модель реактора идеального смешения:
Слайд 53. Модель реактора идеального вытеснения:
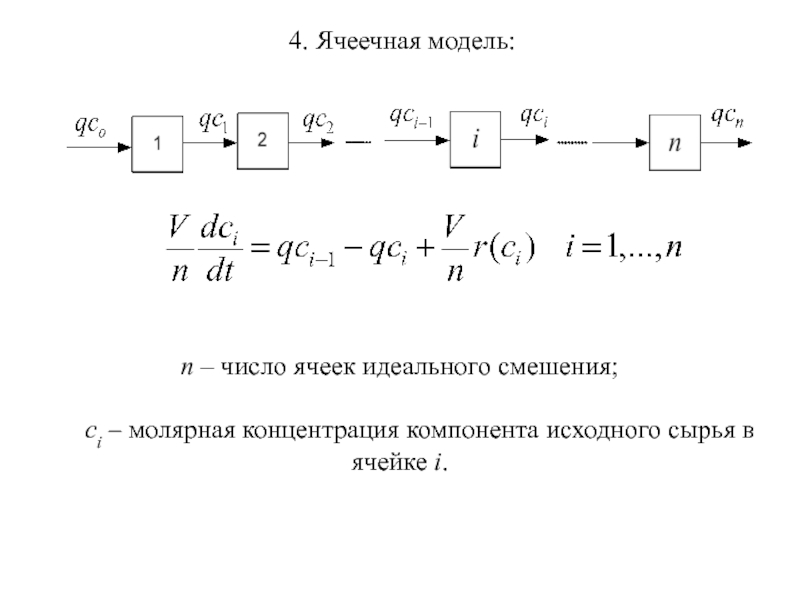
Слайд 64. Ячеечная модель:
n – число ячеек идеального смешения;
ci – молярная
концентрация компонента исходного сырья в ячейке i.
Слайд 75. Однопараметрическая диффузионная модель:
Слайд 86. Двухпараметрическая диффузионная модель:
Слайд 97. Реакция идёт с изменением объёма:
7.1 Реактор периодического действия (V
≠ const)
Слайд 107.2 Реактор идеального вытеснения (V ≠ const)
Слайд 11Выбор конструкции жидкофазного реактора
1. Селективность.
2. Удельная производительность.
3. Концентрация целевого продукта
на выходе
1. Параллельные реакции первого порядка.
- селективность не зависит от
типа аппарата и от степени превращения, а зависит только от условий проведения процесса: температура, соотношение реагентов и др.
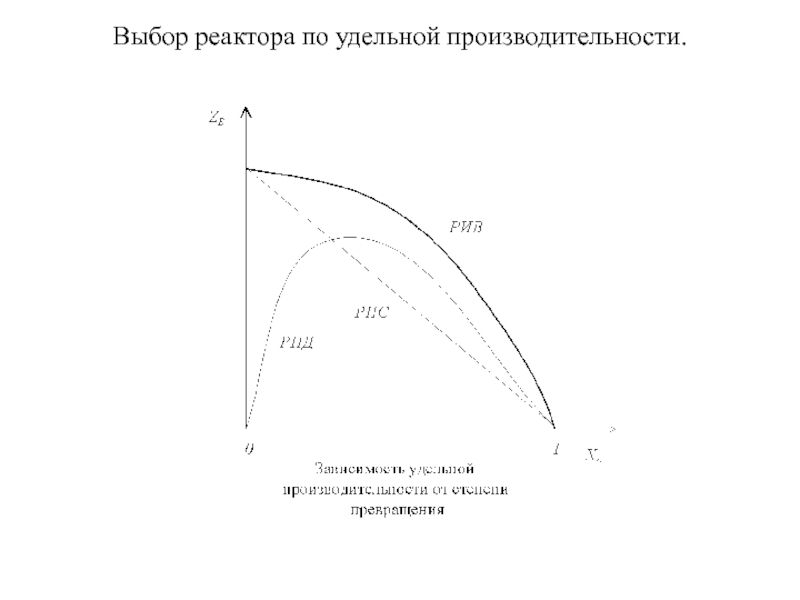
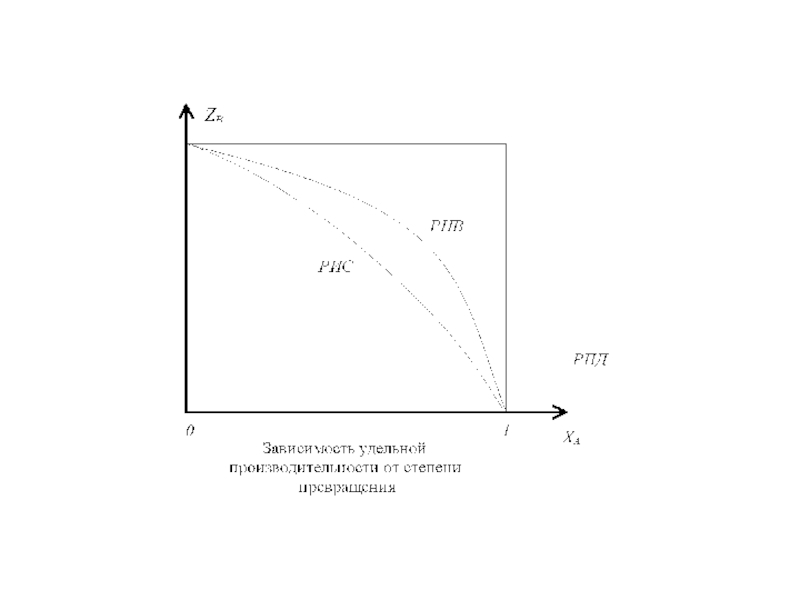
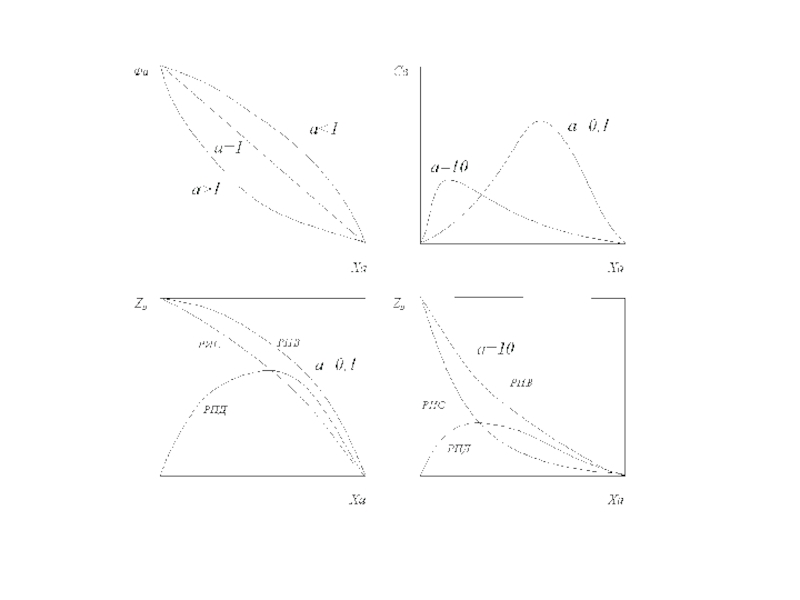
Слайд 12Выбор реактора по удельной производительности.
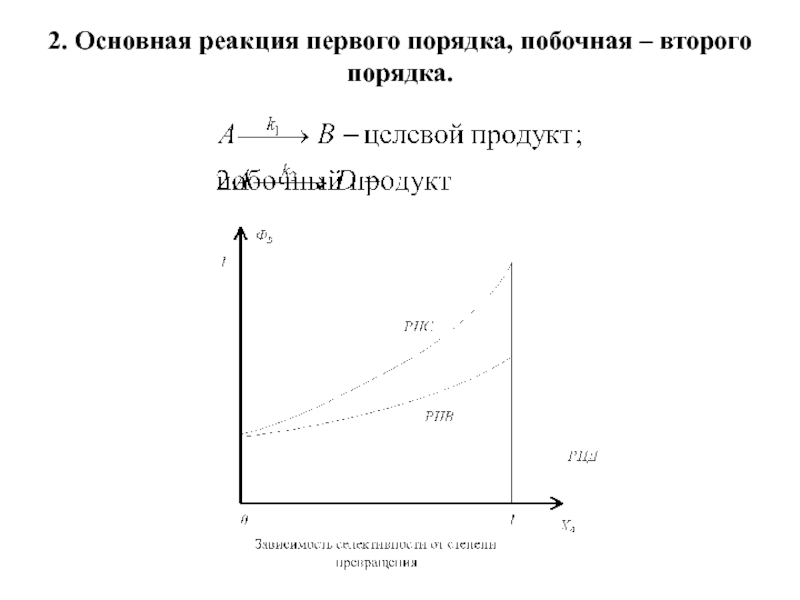
Слайд 132. Основная реакция первого порядка, побочная – второго порядка.
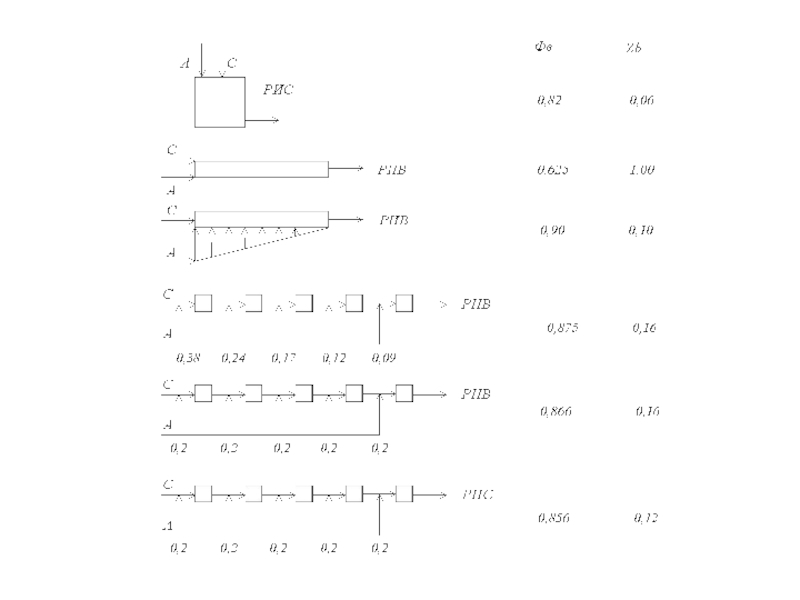
Слайд 15Пример. Варианты аппаратурного оформления реакционного узла.
(С - в избытке,
реакция псевдопервого порядка)
Слайд 173. Последовательные реакции первого порядка
Селективность уменьшается с увеличением степени превращения
и всегда больше в реакторе идеального вытеснения.
Удельная производительность всегда
больше в реакторе идеального вытеснения.
Слайд 19Расчёт жидкофазных реакторов.
(в реакторе протекает одна химическая реакция)
Расчёт жидкофазного реактора
с использованием модели идеального вытеснения.
Слайд 20Исходные данные: q, co, c (или x), r(c) (одна химическая
реакция). Найти: d и L
Слайд 21Расчёт жидкофазного реактора с использованием модели идеального смешения.
Исходные данные: q,
co, c (или x), r(c) (одна химическая реакция).
Найти: V
Слайд 22Расчёт каскада реакторов идеального смешения
Исходные данные: q,co,V, протекает одна реакция
ri(ci) , i=1,2,…,n, cn
сырьевого компонента на выходе из каскада.
Рассчитать: n – число реакторов в каскаде.
Уравнение материального баланса для реактора под номером i:
Слайд 23Расчёт проводим в следующей последовательности:
1. Рассчитываем время пребывания:
2. Рассчитываем первый
реактор, i =1:
Решаем уравнение (в общем случае нелинейное) и находим
концентрацию на выходе из первого реактора – с1.
Слайд 24и так далее.
Если с2 < смах, то расчёт закончен (в
каскаде два реактора). Если с2 > смах, полагаем i =3
и продолжаем расчёт.
Если в системе протекает M реакций, то на каждой итерации решается система в общем случае нелинейных уравнений порядка М.
3. Сравниваем полученное значение с смах:
Если с1 < смах, то расчёт закончен (в каскаде один реактор). Если с1 > смах, полагаем i =2 и продолжаем расчёт:
Слайд 25Расчёт жидкофазного реактора с использованием ячеечной модели
n – число ячеек
идеального смешения;
ci – молярная концентрация компонента исходного сырья в ячейке
i.
Пусть в реакторе протекает одна химическая реакция:
А + ……. → ….. продукты.
Исходные данные: q, co, cn , r(c)
Необходимо рассчитать: cn, L, d.
Слайд 26Алгоритм расчёта:
Выбираем режим движения жидкости, задавшись значением критерия Рейнольдса (Re).
Зная
объёмный расход q, рассчитываем диаметр реактора d (см. расчёт реактора
по модели идеального вытеснения).
3. Рассчитываем коэффициент продольной диффузии
Задаёмся длиной реактора L (длина будет корректироваться в ходе расчёта).
5. Рассчитываем диффузионный критерий Пекле:
Слайд 27Рассчитываем значение числа ячеек идеального смешения n по тем или
иным эмпирическим формулам, зная Pe.
Решаем систему уравнений материального баланса и
находим концентрацию на выходе из реактора – cpn.
Сравниваем расчетное значение концентрации cpn с заданным значением с. Если они не совпадают с заданной степенью точности, то корректируем длину реактора и повторяем расчёт с пункта 5. Так как n – целое число, достаточно, чтобы расчётная концентрация на выходе из реактора была немного меньше, чем заданное.
9. В результате расчёта получаем длину L и d - диаметр аппарата.
Слайд 28Расчёт жидкофазного реактора с использованием однопараметрической диффузионной модели
Слайд 29Рассмотрим статический режим работы реактора:
Слайд 30На графике приведена зависимость концентрации компонента с по длине реактора
l:
Введём новую переменную (y) и преобразуем уравнение материального баланса к
следующему виду:
Граничные условия:
Слайд 31Исходные данные: q, co, ck , r(c)
Необходимо рассчитать: lk ,
d.
Расчёт проводим в следующей последовательности:
Выбираем режим движения жидкости, задав значение
критерия Рейнольдса – Re.
Рассчитываем диаметр реактора и линейную скорость движения жидкости: d и w.
Задаёмся длиной реактора lk=L.
4. Рассчитываем коэффициент продольной диффузии
Задаёмся концентрацией при cl=0 = c*. В ходе расчёта концентрация будет корректироваться.
Слайд 326. Рассчитываем y при l=0:
7. Интегрируем систему дифференциальных уравнений
материального баланса от l=0 до l=lk при начальных условиях: сl=0
до yl=0 и рассчитываем профиль концентраций по длине реактора.
8. Проверяем условие:
Если «нет» – корректируем значение cl=0 и повторяем расчёт с пункта 6. Если «да» - идём к пункту 9.
9. Проверяем условие:
Если «нет» - корректируем значение lk и повторяем расчёт с пункта 5. Если «да» - расчёт закончен. Принимаем значение lk на текущей итерации, диаметр реактора рассчитан в п.2.
Слайд 33Общий алгоритм расчёта реактора при произвольном числе реакций
Обозначения:
- qj –
объёмный расход одного из компонентов исходного сырья – j;
- хk
- степень превращения одного из компонентов к исходного сырья;
- φs - селективность образования целевого компонента по компоненту s исходного сырья;
- ri(с1,c2,...,cn) - скорость образования или исчезновения компонента i по всем химическим реакциям.
- d - диаметр реактора;
- L - длина реактора;
- V - объем реактора;
- ci - молярная концентрация компонента i.
Слайд 34Исходные данные: - qj, φk, хk, ri(с1,c2,...,cn), состав исходного сырья
и др. Рассчитать: d,L,V, ci
1. Задаемся значениями факторов, влияющих на
селективность образования целевого продукта (температура, соотношение между реагентами, степень превращения компонентов исх. сырья и др);
2. Рассчитываем объемный расход реакционной массы q и начальные концентрации компонентов cio.
3. Задаемся временем пребывания реакционной массы в реакторе - τ (это отношение V/q).
4. Для модели идеального смешения рассчитываем объём реактора: V=qτ.
5. Для модели идеального вытеснения задаёмся диаметром аппарата d и рассчитываем площадь сечения реактора S=πd2/4, линейную скорость движения жидкости w=q/S и длину реактора L=wτ.
Слайд 356. Для реального аппарата выбираем режим движения жидкости в реакторе,
задавшись соответствующим значением критерия Re. Рассчитываем диаметр d=4qρ/Reπμ, площадь сечения
S=πd2/4, линейную скорость, w=q/S и длину реактора L=wτ.
При использовании для расчёта ячеечной модели рассчитываем параметр ячеечной модели m – число ячеек идеального смешения.
При использовании для расчёта диффузионной модели рассчитываем параметры модели – коэффициенты диффузии в продольном Dl и (или) радиальном направлении Dr.
7. Решаем систему уравнений материального баланса (составленных для каждого компонента) и рассчитываем концентрации всех компонентов на выходе из реактора.
8. Рассчитываем степень превращения компонента k исходного сырья хk и селективность образования целевого продукта по компоненту s исходного сырья - φs.
Слайд 369. Если степень превращения компонента k не равна заданной, то
корректируем время пребывания реакционной массы и повторяем расчёт с пункта
4. Если совпадает с определённой точностью, переходим к пункту 10.
10. Если селективность образования целевого продукта по компоненту s исходного сырья не равняется заданной φs, то корректируем значения факторов, влияющих на селективность процесса и повторяем расчёт с пункта 2.
Если значение селективности равно заданному (с определённой точностью), то расчёт закончен.
Результаты расчёта: d, L, V, сi - концентрации компонентов на выходе из реакторов.
Слайд 37Расчёт реакторов периодического действия
Исходные данные:
- В реакторе протекает одна реакция;
Qс – суточная производительность по сырью;
сo – начальная концентрация
ключевого компонента исходного сырья в реакционной массе;
с – конечная концентрация ключевого компонента;
r(c) – зависимость скорости химической реакции от концентрации.
Необходимо рассчитать:
- объём реактора (объём реакционной массы в реакторе);
- число реакторов.
Слайд 38Расчёт проводим в следующей последовательности:
1. Рассчитывают период периодического процесса (Δτ)
– время от начала одной операции до начала последующей операции:
-
загрузка исходных веществ - τ1;
- нагрев - τ 2;
- химическое превращение - τ 3;
- охлаждение реакционной массы - τ 4;
- выгрузка продуктов - τ 5;
- подготовка реактора к следующей операции - τ 6.
2. Δτ = 1+ τ 2+ τ 3+ τ 4+ τ 5+ τ 6;
Слайд 393. Для расчёта объёма реактора составляем пропорцию:
За 24 часа
необходимо переработать сырья (1+ z)Qс
За Δτ - всё сырьё, которое
находится в реакторе, т.е. φnV,
число реакторов объема V
число операций в сутки
где φ - коэффициент заполнения реактора (0,4 - 0,9), z-запас производительности (5 - 20%).
Слайд 404. Проводим теплотехнический расчёт по стадиям и находим количество
тепла, которое нужно подвести или отвести на каждой стадии.
τ- время
проведения стадии охлаждения или нагрева.
Δtcp- средняя разность температур.
К – коэффициент теплопередачи.
F – площадь поверхности теплообмена.
Для процесса охлаждения:
где Т1 и Т2 – начальная и конечная температуры охлаждаемой жидкости;
t1 и t2 – начальная и конечная температура нагреваемой жидкости (хладогента).
Слайд 41Для процесса нагрева:
где t1 и t2 – начальная и конечная
температуры нагреваемой жидкости;
T1 и T2 – начальная и конечная температура
охлаждаемой жидкости (теплоносителя).
5. Рассчитываем количество теплоносителей, подаваемых в реактор на каждой стадии.