Профессор Е.Ю.Клименко Криогенные и сверхпроводящие электроэнергетические

Двухжидкостная модель (Гортер (1907-1980), Казимир (1909-2000)
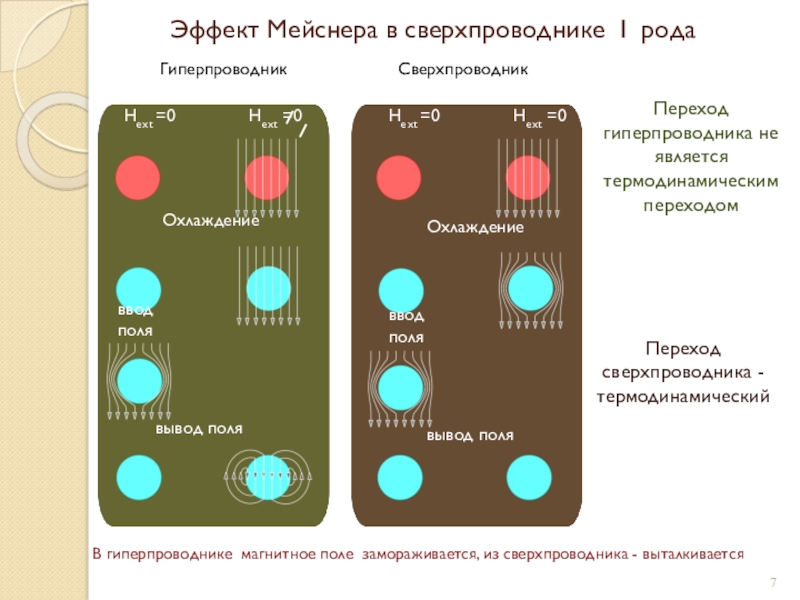
1933- Эффект Мейснера (1882-1974)-Оксенфельда (1901-1993

)
1935- Уравнение Лондонов Фриц (1903-1953), Хайнц (1907-1970)
1953 – Нелокальная теория А.Пипард ( 1920-2008)
1957 – БКШ теория Бардин (1908-1991), Купер (1930), Шриффер (1931)

Камерлинг Оннес Хейке

Казимир Хендрикс

Гортер Корнелис Якоб

Мейснер, Вальтер Фриц

Оксенфельд Роберт

Лондоны Фриц и Хайнц

Пиппард Альфред Брайан

Шриффер Джон Роберт
Бардин Джон, Купер Леон

температуры при приближении к абсолютному нулю. Получив в 1908

жидкий гелий , Камерлинг-Оннес взялся за проверку этих гипотез и открыл сверхпроводимость.

Температурный ход сопротивления ртути

вводят постоянные магниты,
которые удаляют после охлаждения колец,
индуцируя в

них токи одного направления.
Закручивая нить, выводят кольца из одной
плоскости. За углом скручивания наблюдают
с помощью закрепленного на нити зеркальца.
Пока в кольцах есть ток, они
стремятся вернуться в одну плоскость.
Затухание тока можно бы
обнаружить по перемещению зайчика,
но не обнаружено



Уменьшая L и s и увеличивая время наблюдения,
можно получать все более точные оценки r
сверху:
Камерлинг_Оннес и Тюин (1924) R< 10-15Rкомн
Куинн и Иттнер (1962) r<4.10-23Ом см

Сейчас неприлично полагать, что сопротивление
сверхпроводника не равно тождественно нулю.

чтобы состояние материала не зависело от пути, которым он переведен

в это состояние.

Рассмотрим два пути из состояния А в состояние В:
Охлаждение в нулевом поле с последующим подъемом поля.
Охлаждение в магнитном поле

Hext =0
Комнатная температура
Hext =0

Hext =0

Охлаждение

Охлаждение

ввод
поля

ввод
поля

вывод поля

вывод поля

В гиперпроводнике магнитное поле замораживается, из сверхпроводника - выталкивается

Переход гиперпроводника не является термодинамическим переходом

Переход сверхпроводника -термодинамический

проникает в металл.
Из уравнений Максвелла и , взяв ротор из первого, получаем
или ,

поскольку

Уравнение для Bz



Решение:

т.к.


Амплитуда поля убывает экспоненциально. Имеется сдвиг по фазе по мере углубления в металл.
Если в гиперпроводнике , то ток должен течь по поверхности при толщине слоя равной нулю !

До 1933 г. было известно единственное свойство сверхпроводника – бесконечная проводимость.

H e l l e r и F. S a

u t e r в 1933 г. рассмотрели случай гиперпроводника
детальней: Если нет сопротивления, то электроны ускоряются электрическим

полем: причем , тогда

где Взяв ротор от обеих частей последнего уравнения

и, воспользовавшись уравнением Максвелла , получим:

Проинтегрировав его по времени получим

т.е. изменение поля проникает на глубину . А В0 – поле, существовавшее в материале до изменения внешнего поля.
После открытия Мейснером явления выталкивания магнитного поля из сверхпроводника Лондонам не оставалось ничего иного, как положить B0=0

и
в сочетании с материальным уравнением материала.
Для нормальных металлов материальное уравнение – закон Ома.
Для сверхпроводников I рода – уравнения Лондонов:
описывает ускорение носителей электрическим полем

описывает выталкивание поля из объема сверхпроводника.

Действительно, если взять ротор от первого из уравнений Максвелла,
Получим:

) exp(-x/ )
J= Hвнеш = j(0)lL

Индуктивность соленоида (поток Ф в образце) зависит от глубины проникания поля в образец.
Индуктивность с высокой точностью определяется по частоте колебаний в LC-контуре.

СП образец

Характер проникания поля и тока в полубесконечный сверхпроводник с плоской границей

Измерение глубины проникания

переход в промежуточное состояние
Так быть не может !

полученная методом ферромагнитных порошков. Тёмные полосы - выход на поверхность

n-доменов, светлые - S-доменов.

При Нвн <Нс возможны ситуации, когда свободная энергия полностью экранированного сверхпроводника больше свободной энергии нормального состояния, а свободная энергия нормального металла с проникшим полем больше свободной энергии сверхпроводника . В этом случае возникает промежуточное состояние: сверхпроводник разбивается на нормальные и сверхпроводящие области. Тонкость разбиения ограничивается тем, что энергия границы в сверхпроводниках
1 рода положительна.

в проволоке из СПI создает на её поверхности критическое поле.

Поле

на поверхности проволоки при симметричном распределении тока отсюда .

Вычислим плотность критического тока. Он течет на глубине проникания .

У олова Bc = 0.0305 Тл, =5.1Е-8 м получаем jc = 4.76 E11 А/м2.
Эта величина соответствует критической скорости носителей и называется «током распаривания»
Если рассчитать плотность тока на полное сечение проволоки
то для проволоки диаметром 1 мм получим 9.7Е7 А/м2.

У технических сверхпроводников эта величина на два порядка выше.

магнитным полем, нет нужды вводить третье измерение (ток) в фазовую

диаграмму.

При описании технических сверхпроводников нам потребуется трехмерное пространство T-B-j.
Увидим, что переход технического сверхпроводника с током в нормальное состояние не является термодинамическим (результат зависит от пути).

Гиббса

. Две фазы находятся в равновесии, когда равны их гиббсовские потенциалы.
Для простоты рассматривают длинный цилиндр в продольном поле, т.е. в отсутствие промежуточного состояния. Отсутствие поля в объеме

сверхпроводника означает, что оно совершило работу



Если в нормальном состоянии металл не магнетик, то

Получаем для определения критического поля

Дифференцируя по температуре (поскольку ), получаем



В нулевом поле энтропии равны, т.е. переход 2 рода без выделения тепла.
В магнитных полях переход 1 рода с поглощением тепла.

T=Tс и в нулевом поле



Эксперимент показывает, что при

критической температуре имеется
скачок теплоемкости.
Описанный подход позволяет рассчитать
механические эффекты при
сверхпроводящем переходе,
Установить связь между магнитными и
Тепловыми свойствами сверхпроводника,
Но это за пределами курса, так как нас
будут интересовать технические
сверхпроводники .

предсказал, что магнитный поток дискретен:Ф=nh/e=nФo.
В действительности нужно иметь в

виду , что ток переносится парами электронов

Фo=h/2e= 2,067833636(81)Е(-15) Вб.


В июне 1961 года две группы экспериментаторов – Б.С.Дивер и У.М.Фэрбенк (Стенфордский ун-т, Калифорния, США), и Р.Долл и М.Нёбауэр (Баварская Академия наук, Германия) объявили об открытии квантования магнитного потока.

говоря, сила, действующая на трубочку во внешнем магнитном поле, перпендикулярном

ее оси. Трубочка, напыленная на кварцевую нить, подвешивалась на крутильном подвесе. В перпендикулярном направлении прикладывалось переменное магнитное поле Нx , величина которого была известна. Это поле создавало переменный  
момент силы, который приводил систему в колебание. Частота изменений поля автоматически подбиралась равной собственной частоте колебаний системы. Зная декремент затухания, который измерялся предварительно по затуханию свободных колебаний, и измеряя амплитуду колебаний, можно было определить
величину момента силы и вычислить магнитный момент трубочки и величину потока через нее.

Эксперимент Р.Долла и М.Нёбауэра

оловянные трубочки с внутренним диаметром порядка 1,5・10-3 см и длиной

около 1 см. При этом магнитное поле внутри трубочки, если магнитный поток через нее был равен одному кванту Ф0 равнялось примерно 0,1 гс. Это довольно значительное поле. (Магнитное поле Земли составляет 0,5 гс.) Возле концов трубочки помещались маленькие катушки, предназначенные для измерения создававшегося трубочкой магнитного поля. Каждая из катушек имела 10 000 витков. Во время измерения трубочка колебалась с амплитудой в 1 мм и частотой 1000 гц вдоль своей оси. При этом в измерительных катушках возбуждалась электродвижущая сила, которая и измерялась. Прибор предварительно калибровался так, что величина ЭДС прямо давала значение поля в трубочке. Оказалось, что в пределах точности эксперимента магнитный поток в трубочке действительно мог меняться только скачком