Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Программирование
Содержание
- 1. Программирование
- 2. Алгоритмы являются принципиально важным компонентом информатики, т.
- 3. Модель вычислений RAM Разработка машинно-независимых алгоритмов основывается
- 4. Анализ сложности наилучшего, наихудшего и среднего случая
- 5. Анализ сложности наилучшего, наихудшего и среднего случая
- 6. Асимптотические обозначения Намного легче работать с верхней
- 7. Асимптотические обозначения
- 8. Анализ наихудшего случая и асимптотические обозначения являются инструментами, которые существенно упрощают задачу сравнения эффективности алгоритмов.
- 9. Слайд 9
- 10. Слайд 10
- 11. Скорость роста и отношения доминированияИспользуя асимптотические обозначения,
- 12. Скорость роста основных функций Время исполнения f(n)
- 13. Отношения доминирования факториальные показательные кубические квадратичные суперлинейные линейные логарифмические функции-константы
- 14. Сложение и умножение функций n3+n2+n+1 = O(n3)
- 15. Слайд 15
- 16. Оценка эффективностиСортировка методом выбора: При сортировке этим
- 17. Оценка эффективности
- 18. Умножение матриц
- 19. Оценка эффективности
- 20. Логарифмы и их примененияЛогарифм – это функция,
- 21. Логарифмы и двоичный поискДвоичный (бинарный) поиск (также известен
- 22. Быстрое возведение в степеньДопустим, что нужно вычислить
- 23. Логарифмы и система уголовного судопроизводстваРекомендуемые наказания в
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Модель вычислений RAM
Разработка машинно-независимых алгоритмов основывается на гипотетическом компьютере,
называющемся машиной с произвольным доступом к памяти (Random Access Machine)
или RAM-машиной. Согласно этой модели наш компьютер работает таким образом:для исполнения любой простой операции (+, *, -, =, if) требуется ровно один временной шаг;
циклы и подпрограммы не считаются простыми операциями, а состоят из нескольких простых операций. Нет смысла считать подпрограмму сортировки одношаговой операцией, т. к. для сортировки 1 000 000 элементов потребуется определенно намного больше времени, чем для сортировки десяти элементов. Время исполнения цикла или подпрограммы зависит от количества итераций или специфического характера подпрограммы;
каждое обращение к памяти занимает один временной шаг. Кроме этого, наш компьютер обладает неограниченным объемом оперативной памяти. Кэш и диск в модели RAM не применяются.
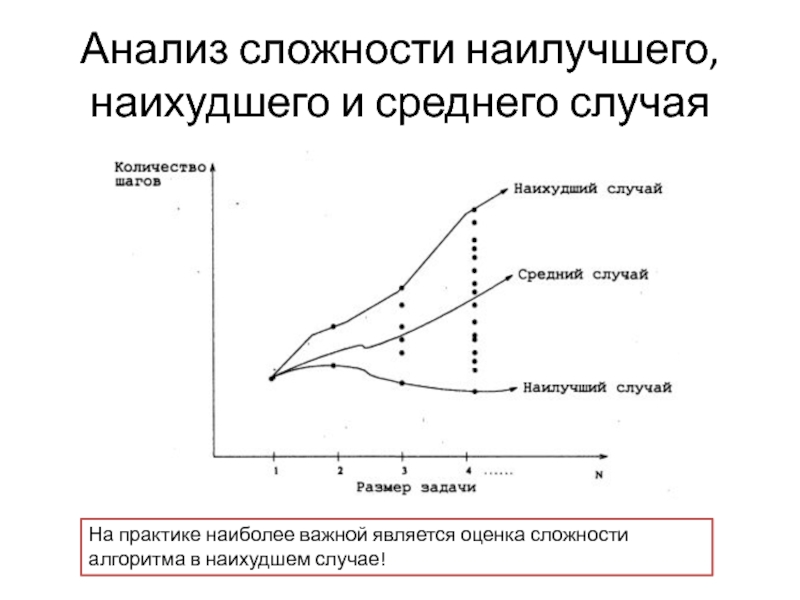
Слайд 4Анализ сложности наилучшего, наихудшего и среднего случая
С помощью RAM-модели
можно подсчитать количество шагов, требуемых алгоритму для исполнения любого экземпляра
задачи. Но чтобы получить общее представление о том, насколько хорошим или плохим является алгоритм, нам нужно знать, как он работает со всеми экземплярами задачи.Чтобы понять, что означает наилучший, наихудший и средний случай сложности алгоритма (т. е. время его исполнения в соответствующем случае), нужно рассмотреть исполнение алгоритма на всех возможных экземплярах входных данных. В случае задачи сортировки множество входных экземпляров состоит из всех возможных компоновок ключей n по всем возможным значениям n.
Слайд 5Анализ сложности наилучшего, наихудшего и среднего случая
На практике наиболее
важной является оценка сложности алгоритма в наихудшем случае!
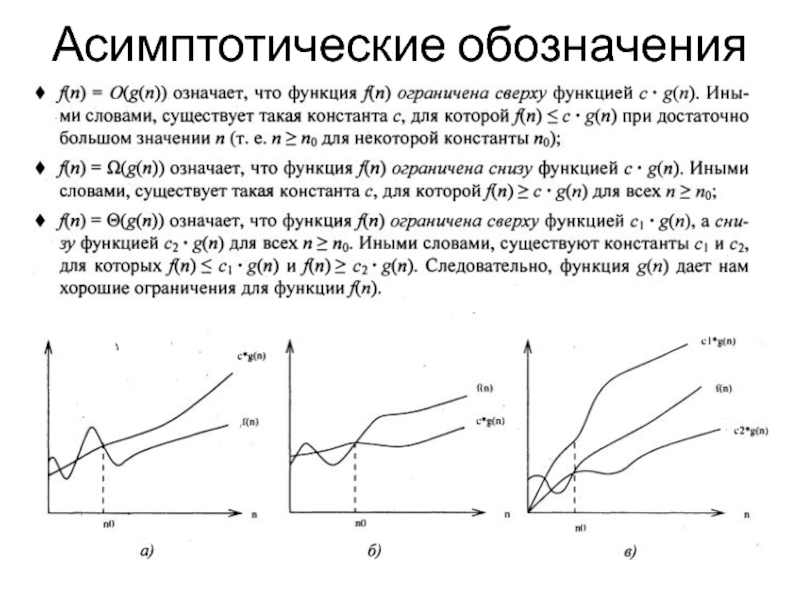
Слайд 6Асимптотические обозначения
Намного легче работать с верхней и нижней границами
функций временной сложности, используя для этого асимптотические обозначения ( -большое
и - большое соответственно).- Неудобно пользоваться
Слайд 8Анализ наихудшего случая и асимптотические обозначения являются инструментами, которые существенно
упрощают задачу сравнения эффективности алгоритмов.
Слайд 11Скорость роста и отношения доминирования
Используя асимптотические обозначения, мы пренебрегаем постоянными
множителями, не учитывая их при вычислении функций.
При таком подходе
функции f(n) = 0,001n2 и g(n) = 1000n2 для нас одинаковы, несмотря на то, что значение функции g(n) в миллион раз больше значения функции f(n) для любого n. Слайд 12Скорость роста основных функций
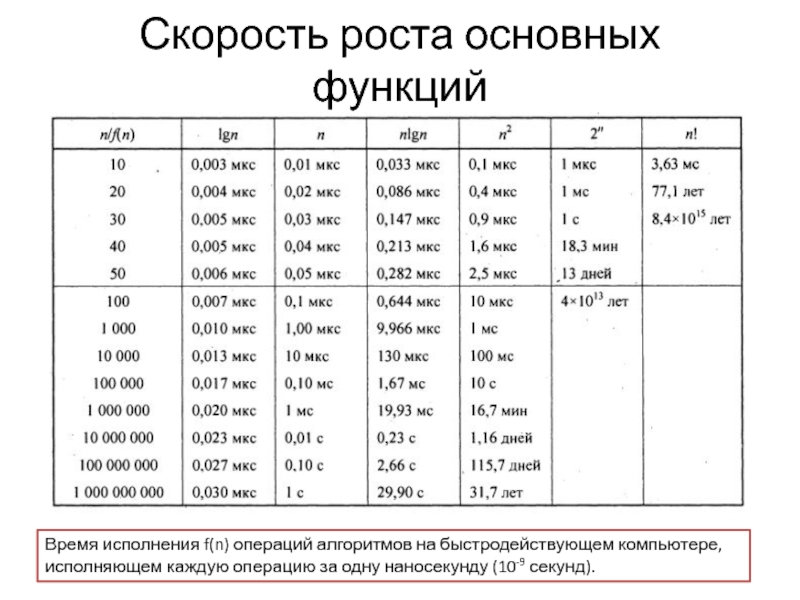
Время исполнения f(n) операций алгоритмов на
быстродействующем компьютере, исполняющем каждую операцию за одну наносекунду (10-9 секунд).
Слайд 13Отношения доминирования
факториальные
показательные
кубические
квадратичные
суперлинейные
линейные
логарифмические
функции-константы
Слайд 16Оценка эффективности
Сортировка методом выбора: При сортировке этим способом определяется наименьший
неотсортированный элемент и помещается в конец отсортированной части массива. Процедура
повторяется до тех пор, пока все элементы массива не будут отсортированы.Слайд 20Логарифмы и их применения
Логарифм – это функция, обратная показательной.
Показательные функции
возрастают чрезвычайно быстро. Соответственно, функции, обратные показательным, т.е. логарифмы, возрастают
довольно медленно.Слайд 21Логарифмы и двоичный поиск
Двоичный (бинарный) поиск (также известен как метод деления
пополам и дихотомия) — классический алгоритм поиска элемента в отсортированном массиве (векторе), использующий дробление
массива на половины.Массив разбивается пополам на каждом вызове до тех пор, пока мы не достигнем единицы. Запишем количество элементов в массиве на каждом вызове:
0-я итерация: n
1-я итерация: n / 2
2-я итерация: n / 4
3-я итерация: n / 8
…
i-я итерация: n / 2i
…
последняя итерация: 1
1 = n / 2i
2i = n
i = log(n)
Слайд 22Быстрое возведение в степень
Допустим, что нужно вычислить точное значение an
для достаточно большого значения n. Самый простой алгоритм выполняет (n-1)
операцию умножения (aa …aa). Но можно указать лучший способ решения этой задачи, приняв во внимание, что n = [n/2]+[n/2].Для вычисления конечного значения будет достаточно O(log n) операций умножения.
Слайд 23Логарифмы и система уголовного судопроизводства
Рекомендуемые наказания в федеральных судах США
за преступления финансового мошенничества
Мораль логарифмического роста функций ясна: уж если
воровать, так миллионы.Логарифмические функции возникают при решении задач с повторяющимся делением или удваиванием входных данных.