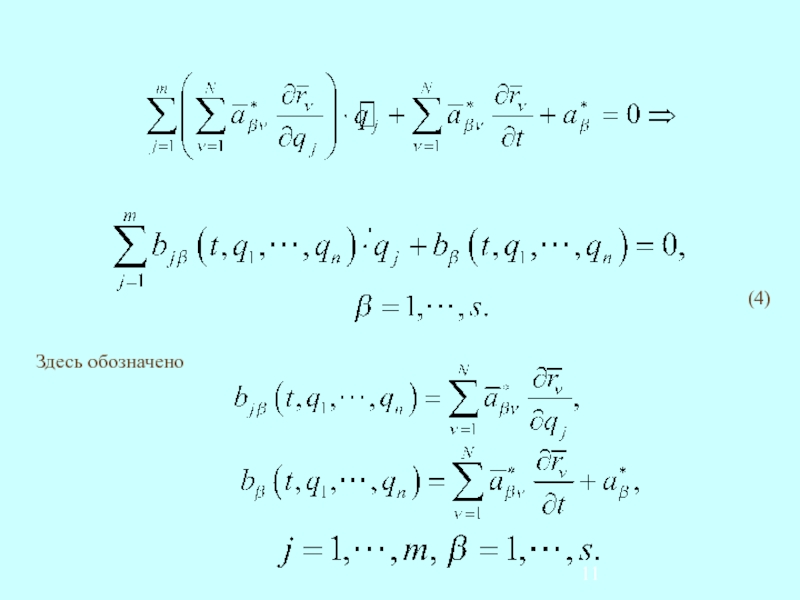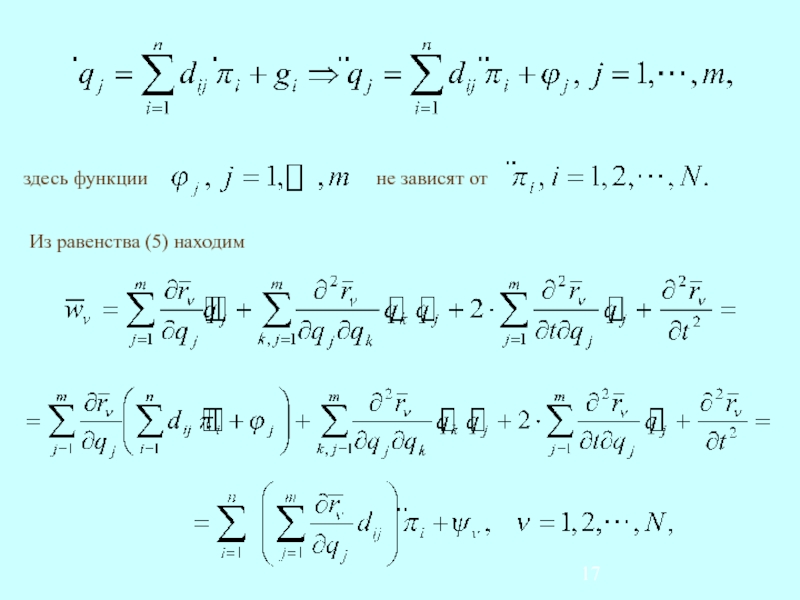Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ
Содержание
- 1. ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ
- 2. 3. ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ3.1. Обобщенные координаты. 3.2.
- 3. 3. ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ3.1. Обобщенные координаты. Очевидно, что
- 4. 2) Зависимость (1) дважды непрерывно дифференцируемая.3) Справедливо равенство
- 5. В общем случае от выполнения
- 6. Пример 3. Математический маятник.
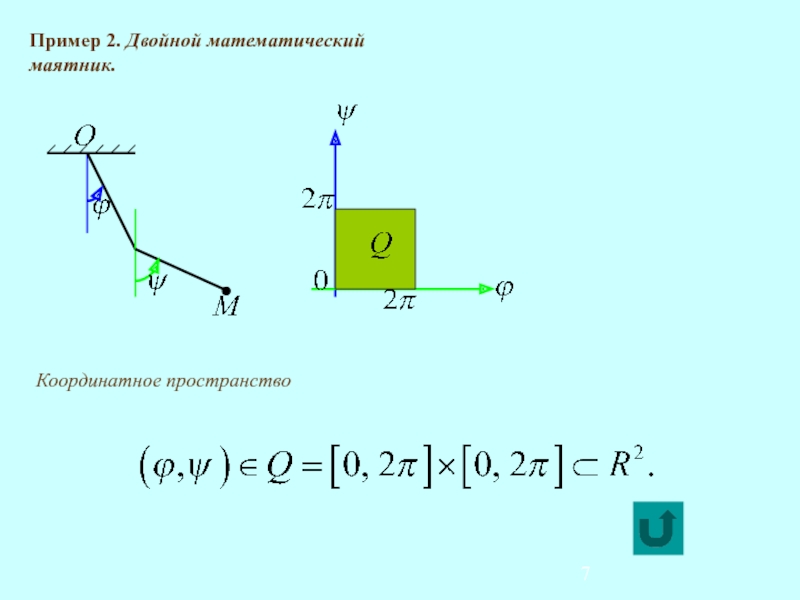
- 7. Пример 2. Двойной математический маятник. Координатное пространство
- 8. 3.3. Обобщенные скорости и ускорения.
- 9. Слайд 9
- 10. Голономные связи. Из (3) находим Неголономные связи. Из (3) и (4) находим
- 11. Здесь обозначено
- 12. Слайд 12
- 13. 3.4. Псевдокоординаты.
- 14. Слайд 14
- 15. Слайд 15
- 16. где обозначено Равенству (6) можно придать другую форму. Имеем
- 17. Из равенства (5) находим
- 18. Таким образом, равенство (6) принимает вид
- 19. Скачать презентанцию
3. ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ3.1. Обобщенные координаты. 3.2. Координатное пространство. 3.3. Обобщенные скорости и ускорения. 3.4. Псевдокоординаты.
Слайды и текст этой презентации
Слайд 2
3. ПРОСТРАНСТВО ОБОБЩЕННЫХ КООРДИНАТ
3.1. Обобщенные координаты.
3.2. Координатное пространство.
3.3.
Обобщенные скорости и ускорения.
Слайд 5 В общем случае от выполнения равенства (2) для
всех допустимых положений системы
можно отказаться. Достаточно ввести локальные обобщенные
координаты. Это означает, что для различных совокупностей возможных положений системы вводятся различные
системы обобщенных координат. При этом для каждой локальной области условие 3)
выполняется.
Заметим. что если система склерономна. То обобщенные координаты можно выбрать
так, чтобы в зависимости (1) не присутствовало время.
3.2. Координатное пространство.