Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка домашнего задания
Содержание
- 1. Проверка домашнего задания
- 2. № 6.19(а,б)уНа координатной плоскости хОу найдите точку,
- 3. № 6.20(а,б)уНа координатной плоскости хОу найдите точку,
- 4. № 6.21(а,б)На координатной плоскости хОу найдите точку,
- 5. № 6.25(а)Постройте отрезок, симметричный отрезку ВК относительно
- 6. № 6.26(а)Постройте отрезок, симметричный отрезку DM относительно оси у, если: D(4; 2), М(1; 6)DМ1D1М
- 7. № 6.27(а)Постройте отрезок, симметричный отрезку СН относительно
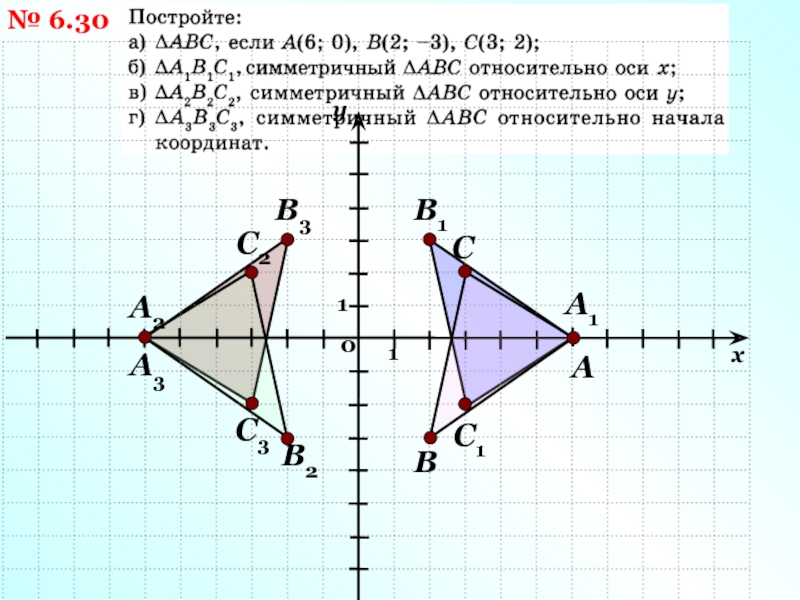
- 8. № 6.30АСВА1В1С1А2В2С2А3В3С3
- 9. К л а с с н а
- 10. РТ № 7.2Составьте аналитическую модель данной ситуации
- 11. РТ № 7.1Запишите в общем виде линейное уравнение с одной переменной:ах + b = 0
- 12. РТ № 7.2Составьте аналитическую модель данной ситуации
- 13. РТ № 7.2Составьте аналитическую модель данной ситуации
- 14. РТ № 7.5Подчеркните те уравнения, которые являются
- 15. РТ № 7.2Составьте аналитическую модель данной ситуации
- 16. 3х + 5у = 9503 · 100
- 17. РТ № 7.6Проверьте, является ли решением уравнения
- 18. РТ № 7.6Найдите ещё какие-нибудь решения уравне-ния
- 19. № 7.10(б)Для данного линейного уравнения найдите значение
- 20. № 7.11(б)Для данного линейного уравнения найдите значение
- 21. № 7.14(б)Для данного линейного уравнения найдите значение
- 22. № 7.25(а)Среди решений уравнения x + 3y
- 23. № 7.26(а)Найдите значение коэффициента a в уравнении
- 24. № 7.27(а)Найдите значение коэффициента b в уравнении
- 25. Дома:У: стр. 39 § 7З: § 7
- 26. Скачать презентанцию
№ 6.19(а,б)уНа координатной плоскости хОу найдите точку, симметричную данной точке, относительно начала координат.а) А(5; 7)б) В(0; 8)АА1А1(– 5; – 7)В1(0; – 8)
Слайды и текст этой презентации
Слайд 2№ 6.19
(а,б)
у
На координатной плоскости хОу найдите точку, симметричную данной точке,
относительно начала координат.
– 8)
Слайд 3№ 6.20
(а,б)
у
На координатной плоскости хОу найдите точку, симметричную данной точке,
относительно оси у.
а) М(– 2; 8)
б) L(– 5; 0)
М
М1
М1(2; 8)
L
L1
L1(5;
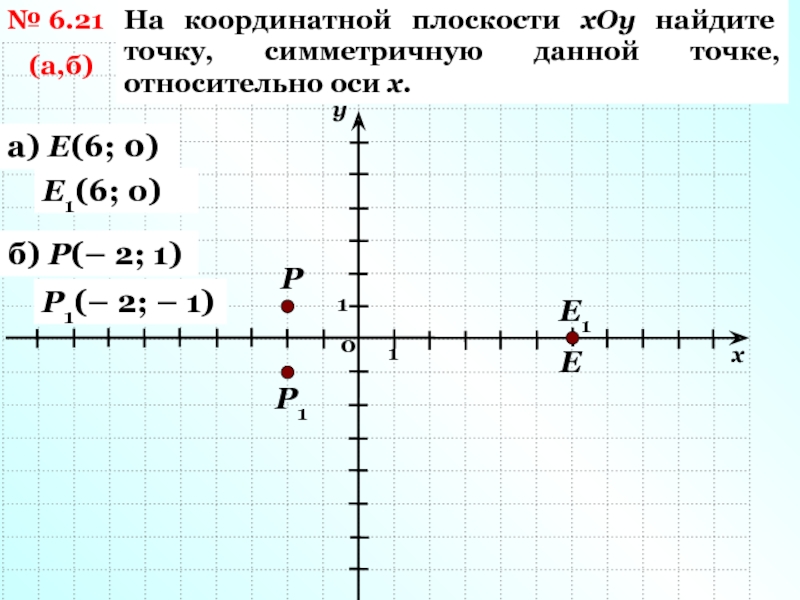
0)
Слайд 4№ 6.21
(а,б)
На координатной плоскости хОу найдите точку, симметричную данной точке,
относительно оси х.
а) Е(6; 0)
б) Р(– 2; 1)
Р
Р1
Е1(6; о)
Е
Е1
Р1(– 2;
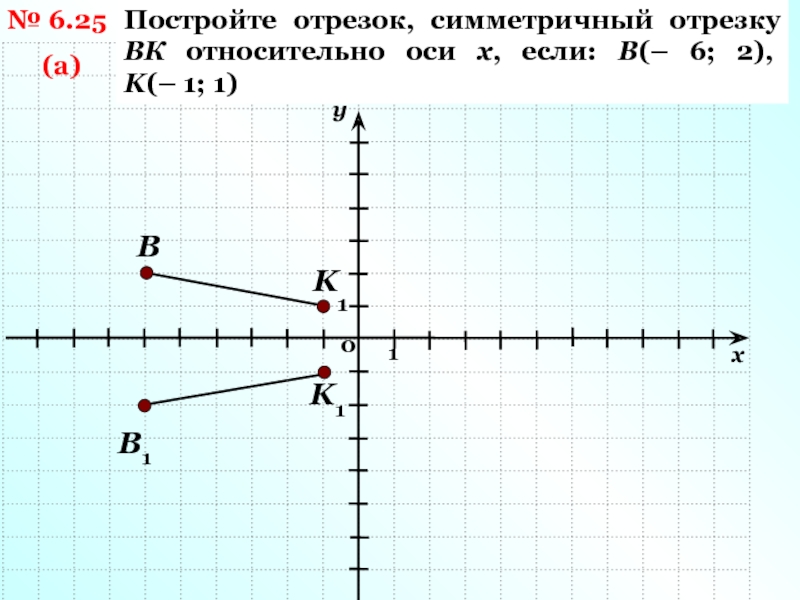
– 1)
Слайд 5№ 6.25
(а)
Постройте отрезок, симметричный отрезку ВК относительно оси х, если:
В(– 6; 2), K(– 1; 1)
K
В
В1
K1
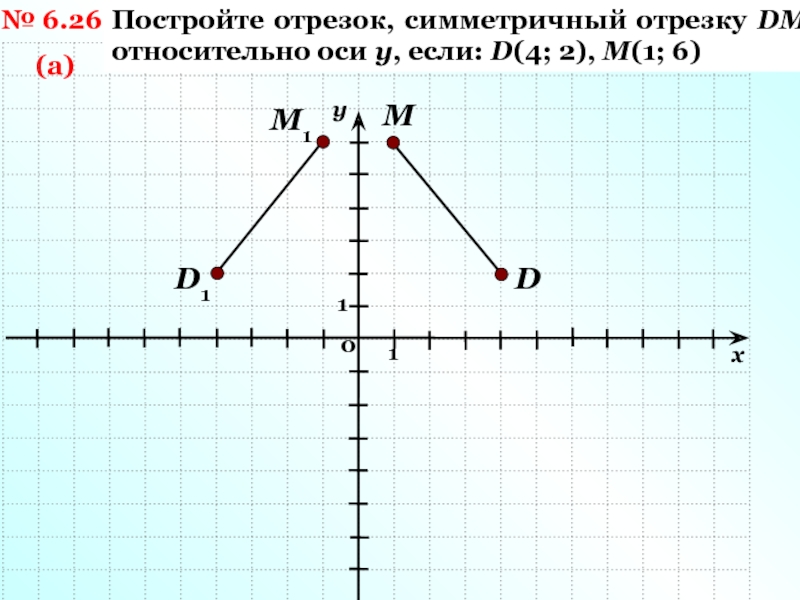
Слайд 6№ 6.26
(а)
Постройте отрезок, симметричный отрезку DM относительно оси у, если:
D(4; 2), М(1; 6)
D
М1
D1
М
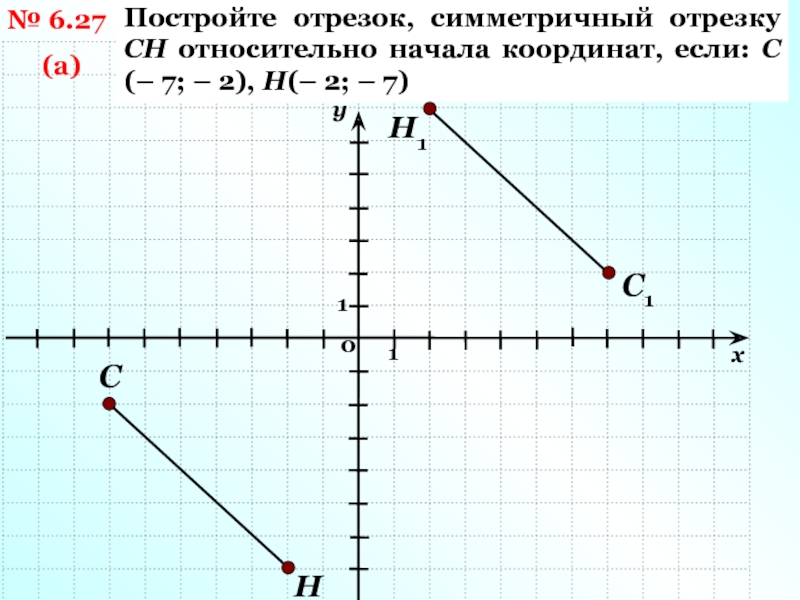
Слайд 7№ 6.27
(а)
Постройте отрезок, симметричный отрезку СН относительно начала координат, если:
С(– 7; – 2), Н(– 2; – 7)
Н
С
С1
Н1
Слайд 10РТ № 7.2
Составьте аналитическую модель данной ситуации – уравнение.
Сколько переменных
содержит полученное уравнение?
а) Мастер в час делает k деталей, а
ученик – 15. Мастер работал 4 ч, а ученик только 1 ч. Всего они сделали 135 деталей. 4k + 15 = 135
одну
Слайд 12РТ № 7.2
Составьте аналитическую модель данной ситуации – уравнение.
Сколько переменных
содержит полученное уравнение?
б) 1 кг винограда стоит х р., а
1 кг абрикосов у р. Боря купил 3 кг винограда и 5 кг аб- рикосов, заплатив за всю покупку 950 р.3х + 5у = 950
две
Слайд 13РТ № 7.2
Составьте аналитическую модель данной ситуации – уравнение.
Сколько переменных
содержит полученное уравнение?
в) Площадь квадрата со стороной р больше площади
квадрата со стороной q на 34 см2р2 – q2 = 34
две
Слайд 14РТ № 7.5
Подчеркните те уравнения, которые являются линейными уравнениями с
двумя переменными:
х – у + 4 = 0;
2х – 3у
– 4 = 0;2х + 3у = 4;
а + b + с = 0;
5m2 – 25n – 10 = 0.
Слайд 15РТ № 7.2
Составьте аналитическую модель данной ситуации – уравнение.
б) 1
кг винограда стоит х р., а 1 кг абрикосов у
р. Боря купил 3 кг винограда и 5 кг аб- рикосов, заплатив за всю покупку 950 р.3х + 5у = 950
Мог ли 1 кг винограда стоить 100 р., а 1 кг абрикосов – 130 р?
3 · 100 + 5 · 130 = 950
да
Мог ли 1 кг винограда стоить 150 р., а 1 кг абрикосов – 120 р?
3 · 150 + 5 · 120 = 950
нет
Слайд 163х + 5у = 950
3 · 100 + 5 ·
130 = 950
верно
3 · 150 + 5 · 120 =
950неверно
х = 100, у = 130
х = 150, у = 120
х = 100, у = 130 или (100; 130) – реше-ние уравнения
Слайд 17РТ № 7.6
Проверьте, является ли решением уравнения 3х + у
– 7 = 0 пара чисел:
а) (1; 4)
б) (– 2;
13)в) (1; – 100)
г) (5; – 8)
3 · 1 + 4 – 7 = 0
является
0 = 0
3 · (– 2) + 13 – 7 = 0
0 = 0
является
3 · 1 + (– 100) – 7 = 0
– 104 = 0
не является
3 · 5 + (– 8) – 7 = 0
0 = 0
является
Слайд 18РТ № 7.6
Найдите ещё какие-нибудь решения уравне-ния 3х + у
– 7 = 0.
РТ № 7.7
Запишите, сколько решений имеет линей-
ное уравнение с двумя переменными:бесконечное количество
Слайд 19№ 7.10(б)
Для данного линейного уравнения найдите значение y, соответствующее заданному
значению x.
5x – 7y – 14 = 0, если x
= 0если x = 0, то 5 · 0 – 7y – 14 = 0
– 7y – 14 = 0
– 7y = 14
y = – 2
Ответ: y = – 2
Слайд 20№ 7.11(б)
Для данного линейного уравнения найдите значение y, соответствующее заданному
значению x.
11x – 13y + 16 = 0, если x
= – 5 если x = – 5, то – 55 – 13y + 16 = 0
– 13y – 39 = 0
– 13y = 39
y = – 3
Ответ: y = – 3
Слайд 21№ 7.14(б)
Для данного линейного уравнения найдите значение x, соответствующее заданному
значению y.
23x – 9y + 5 = 0, если y
= – 2 если y = – 2, то 23x – 9 · (– 2) + 5 = 0
23x + 23 = 0
23x = – 23
x = – 1
Ответ: x = – 1
23x + 18 + 5 = 0
Слайд 22№ 7.25(а)
Среди решений уравнения x + 3y – 20 =
0 найдите такую пару, которая состоит из двух одинаковых чисел
если
x = y, то y + 3y – 20 = 0 4y – 20 = 0
4y = 20
y = 5
Ответ: (5; 5)
Слайд 23№ 7.26(а)
Найдите значение коэффициента a в уравнении ax + 5y
– 40 = 0, если известно, что решением уравнения является
пара чисел (3; 2).если x =3 y = 2, то a · 3 + 5 · 2 – 40 = 0
3a – 30 = 0
3a = 30
a = 10
Ответ: a = 10
Слайд 24№ 7.27(а)
Найдите значение коэффициента b в уравнении 6x + by
– 35 = 0, если известно, что решением уравнения является
пара чисел (0; 1).если x =0 y = 1, то 6 · 0 + b · 1 – 35 = 0
b – 35 = 0
b = 35
Ответ: b = 35
