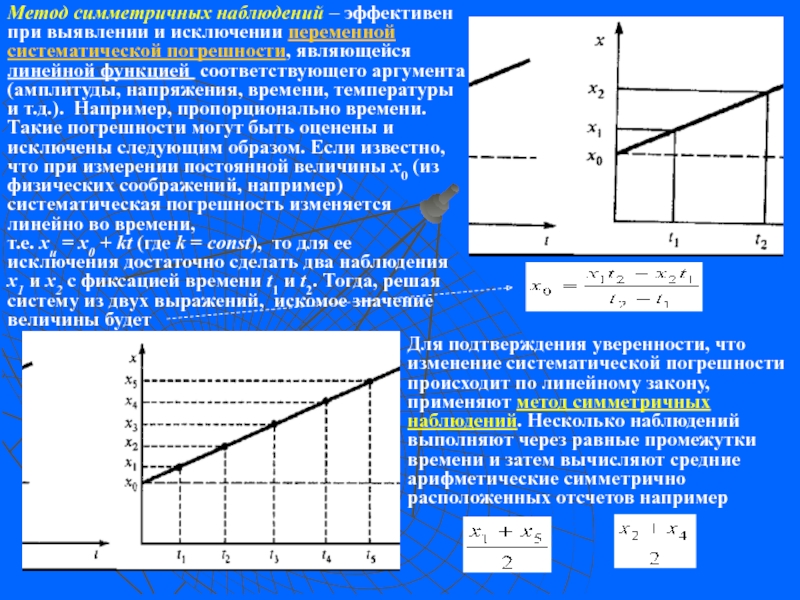
метод применяется для оценки погрешностей при совместных измерениях? Поясните суть
данного метода.
Какие условия применения метода наименьших квадратов Вы знаете?
Как, используя метод наименьших квадратов, построить экспериментальную линейную аппроксимацию? В чем суть правила нахождения коэффициентов а и b методом ?
Как осуществляется выбор средств измерений по точности?
Нормирование метрологических характеристик средств измерений. Какие задачи выполняет нормирование погрешностей?
Какие способы выражения точности измерения определены МИ 1317—86?
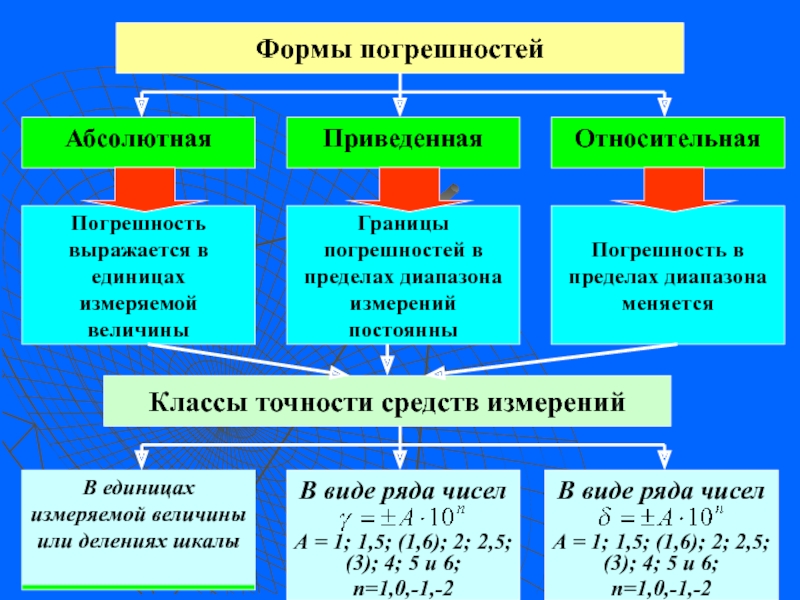
Какие виды классов точности Вы знаете? Как устанавливают класс точности на СИ, имеющих абсолютную, относительную и приведенную формы погрешностей?
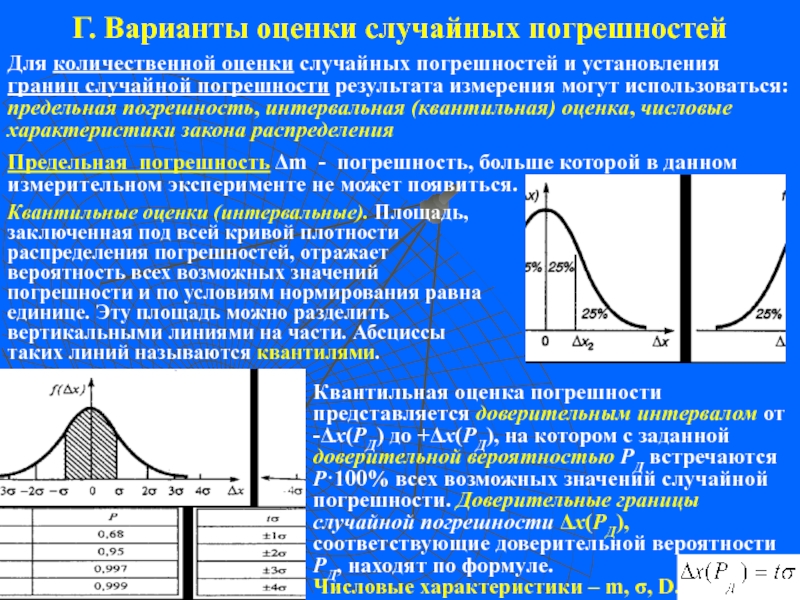
Приведите графики зависимости абсолютной и относительной погрешностей (аддитивной, мультипликативной и суммарной). Сделайте вывод о выборе вида функции нормирования СИ в зависимости от характера изменения погрешности по диапазону.
Формулы вычисления и обозначение классов точности СИ. Какую формулу применяют для обозначения цифровых СИ?
А.Г. Сергеев, М.В. Латышев, В.В. Терегеря. Метрология, стандартизация, сертификация. – М.: ЛОГОС, 2004.
[2] - А.С. Сигов, В.И. Нефедов. Метрология, стандартизация и технические измерения. – М.: Высшая школа, 2008. Стр. 137-157





![Иркутский филиал
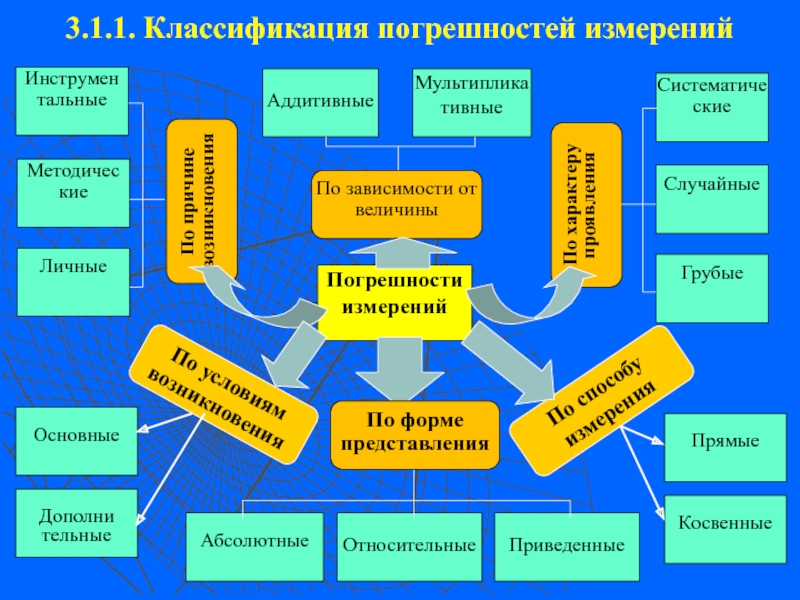
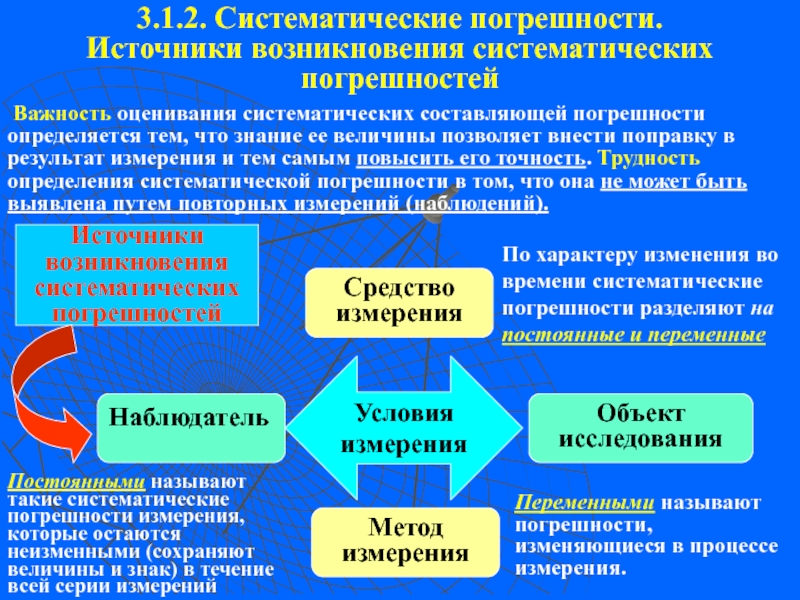
Московского государственного технического университета 3.2. Методы оценки погрешностей измерения ([2], стр.124-137)Не обнаруженная систематическая составляющая погрешности 3.2. Методы оценки погрешностей измерения ([2], стр.124-137)Не обнаруженная систематическая составляющая погрешности опаснее случайной погрешности (случайная погрешность](/img/tmb/3/249053/b4dd5d123f16e6b5467da3083ae1b4b5-800x.jpg)












![Иркутский филиал
Московского государственного технического университета 3.5. Формулы вычисления и обозначение классов точностистр. 133-134, [1] 3.5. Формулы вычисления и обозначение классов точностистр. 133-134, [1]](/img/thumbs/a4e71d2b4d848cc49310a3824c94f470-800x.jpg)