Слайд 1Рабочая тетрадь по начертательной геометрии
Тема 1:
Точка, прямая, плоскость
Слайд 2Точка
Точка в пространстве и на чертеже может быть задана:
Координатами
в прямоугольной системе координат.
Двумя пересекающимися прямыми.
Вершинами гранной фигуры.
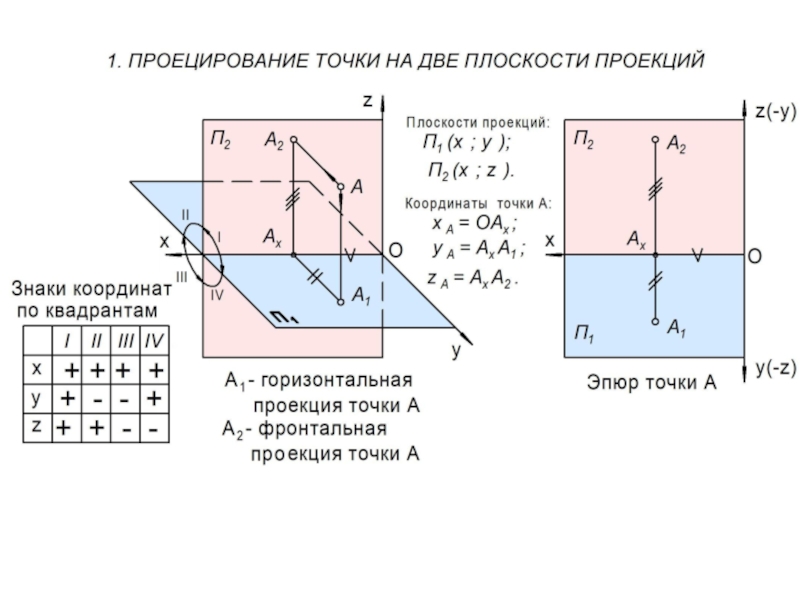
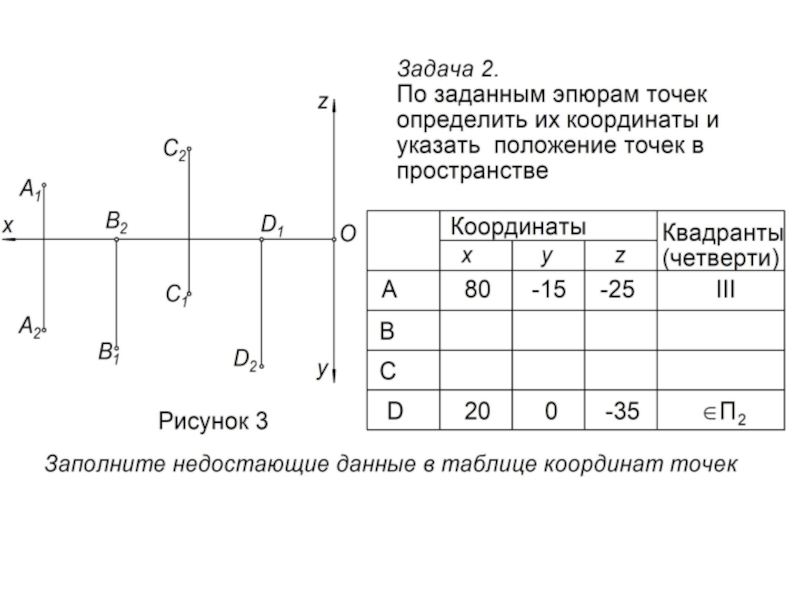
Ортогональный чертеж (эпюр) точки представляет собой совокупность двух ее ортогональных проекций, соединенных линией связи, перпендикулярной координатной оси.
Абсцисса (X) точки А – это отрезок, измеряемый в мм и откладываемый на эпюре по координатной оси 0х влево от начала координат 0.
Ордината (Y) точки А – это отрезок, измеряемый и откладываемый на эпюре по линии связи от координатной оси 0х вниз при положительном значении ординаты и вверх – при отрицательном.
Аппликата (Z) точки А – это отрезок, измеряемый и откладываемый на эпюре по линии связи от координатной оси 0х вверх при положительном значении аппликаты и вниз – при отрицательном.
Слайд 8Прямая
Прямая в пространстве и на чертеже может быть задана:
Двумя точками.
Точкой
и направлением.
Двумя пересекающимися плоскостями.
Рассматриваются:
а) прямые общего положения (они не
параллельны ни одной из трех плоскостей проекций);
б) прямые частного положения:
уровня, т.е. параллельные одной из трех плоскостей проекций, на указанные плоскости они проецируются в натуральную величину (НВ):
- горизонтальные – параллельные П1 ;
- фронтальные – параллельные П2;
- профильные – параллельные П3 .
проецирующие, т.е. перпендикулярные одной трех плоскостей
проекций: П1 ;П2 ; П3 . Эти прямые проецируются на
указанные плоскости вырождено – в виде точки.
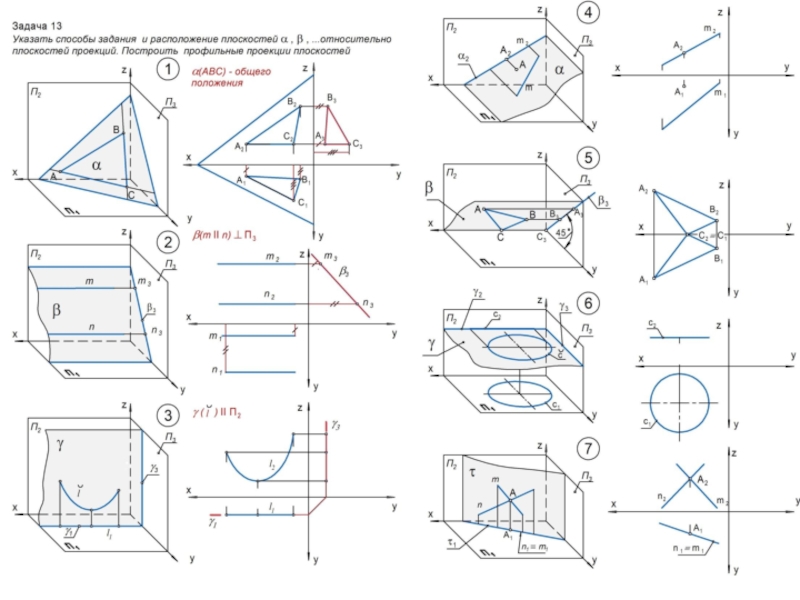
Слайд 16Плоскость
Плоскость в пространстве и на чертеже может быть задана:
1. Тремя точками, не лежащими на одной прямой: (АВС).
2. Прямой и точкой, не лежащей на этой прямой: (l, A).
3. Двумя пересекающимися прямыми: (m n).
4. Двумя параллельными прямыми: (b II c).
5. Плоской кривой ( m).
Рассматривают:
Плоскости общего положения, неперпендикулярные ни одной из трех плоскостей проекций;
Плоскости частного положения:
- проецирующие ( П1 ; П2 ; П3 ), имеющие на
указанных плоскостях вырожденные проекции в виде
прямых линий;
- уровня ( II П1 ; II П2 ; II П3 ), являющиеся дважды
проецирующими.
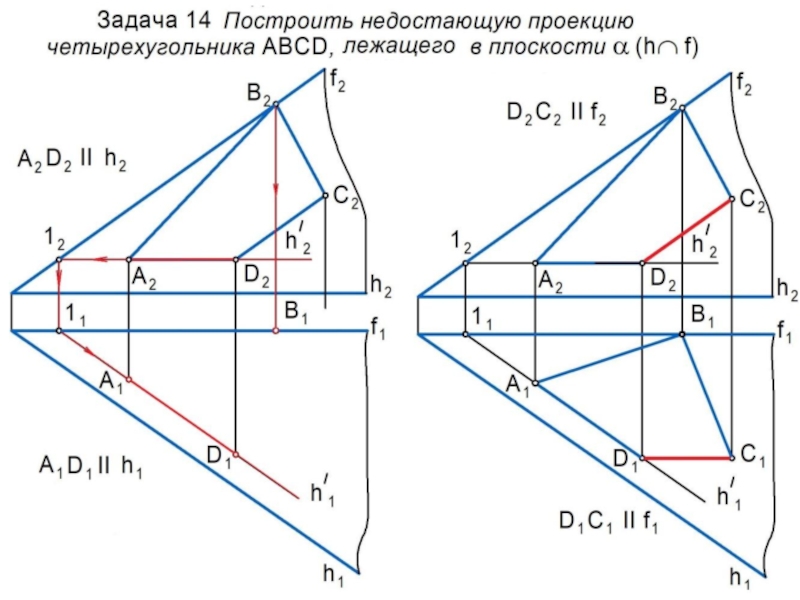
Слайд 18Принадлежность прямой и точки плоскости
Точка принадлежит прямой, если ее проекции
расположены на одноименных проекциях этой прямой: Аm, если А1m1; А2m2.
Точка
принадлежит плоскости, если она расположена на прямой, принадлежащей этой
плоскости.
Прямая принадлежит плоскости, если она:
а) проходит через две точки, принадлежащие
этой плоскости;
б) проходит через точку плоскости и
параллельна линии, лежащей в этой плоскости.
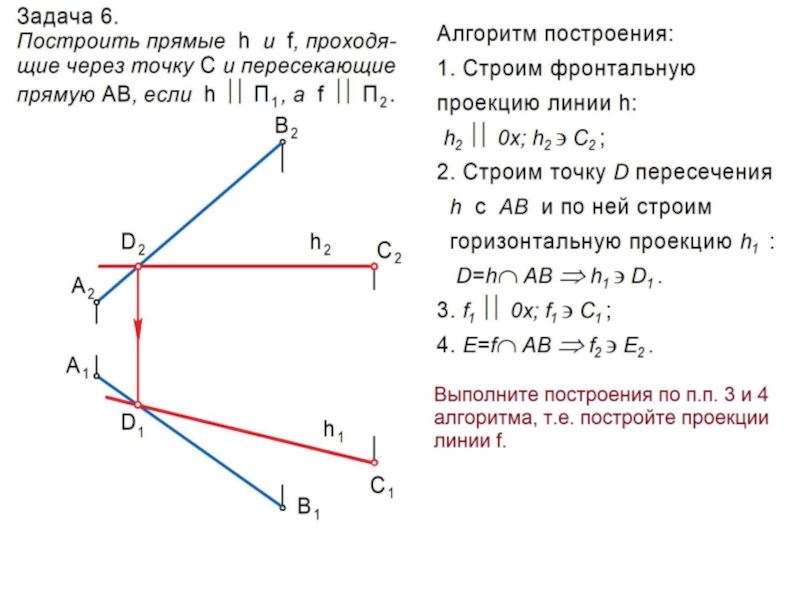
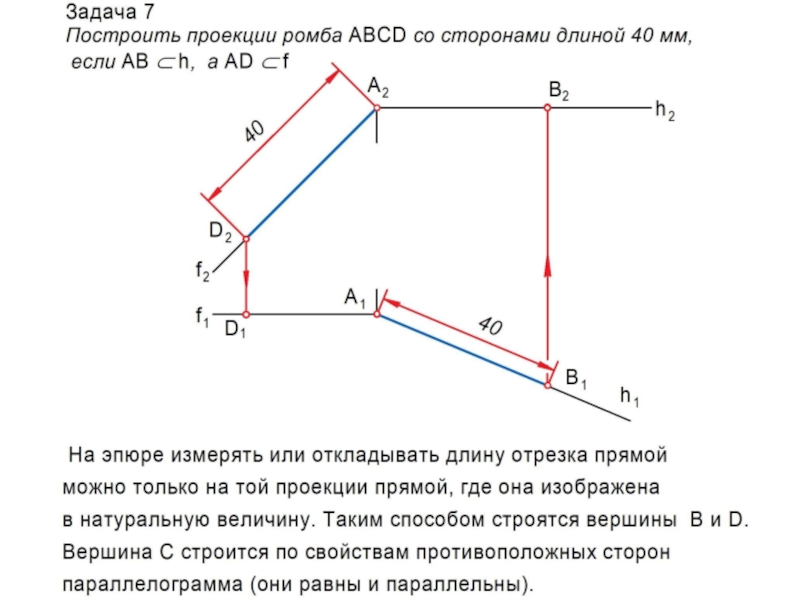
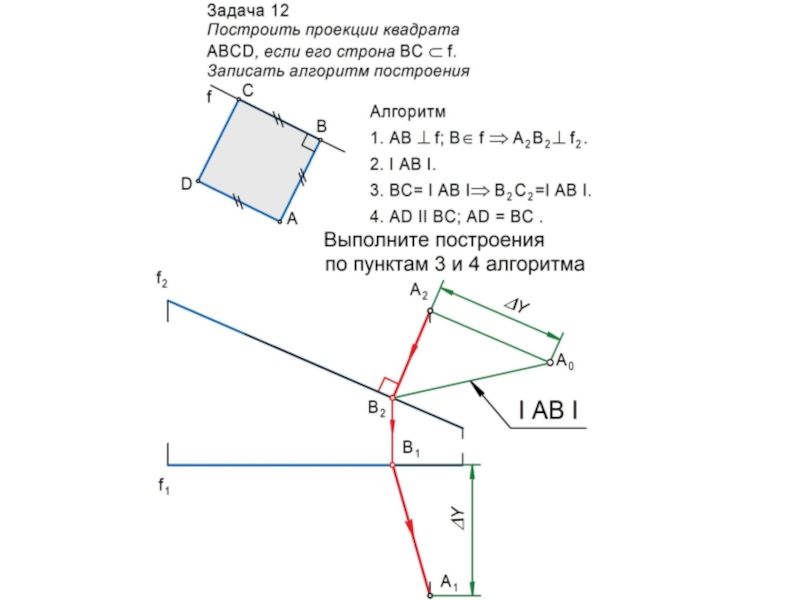
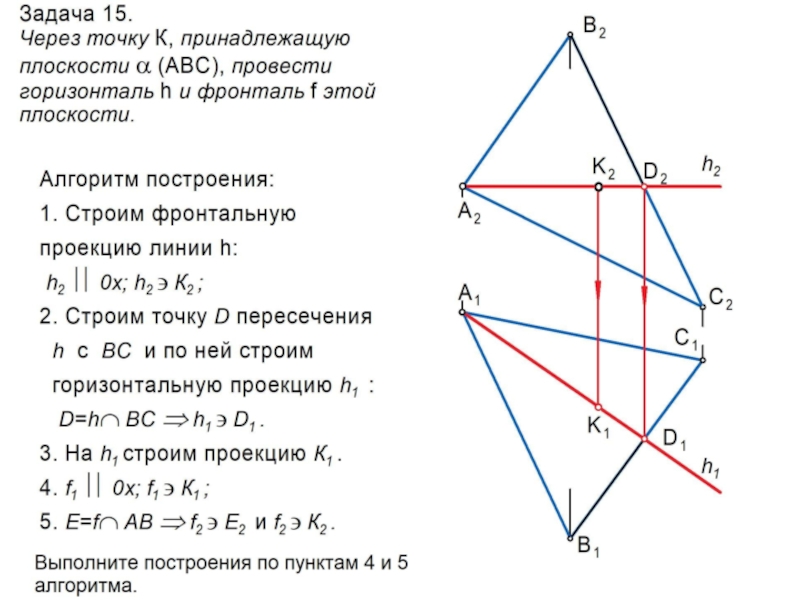
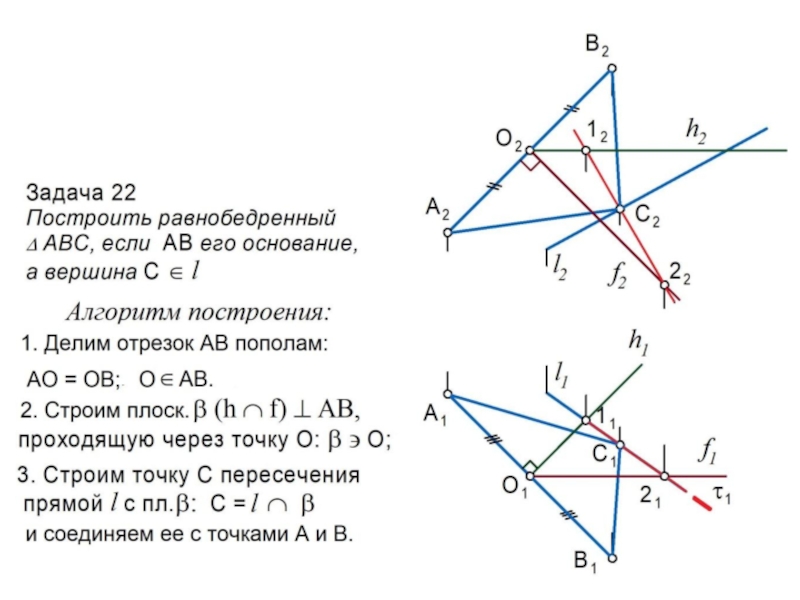
Слайд 20Главные линии плоскости
Горизонталь h – это линия, принадлежащая
плоскости и
параллельная П1 . Ее фронтальная проекция параллельна оси 0х:
h ; h II П1 h2 II 0х.
Фронталь f – это линия, принадлежащая
плоскости и параллельная П2 . Ее горизонтальная проекция параллельна оси 0х:
f ; f II П2 f1 II 0х.
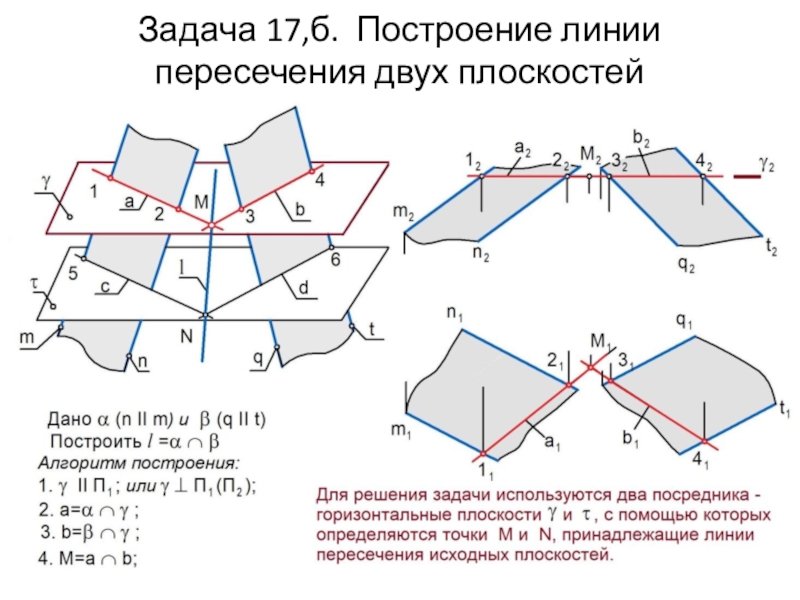
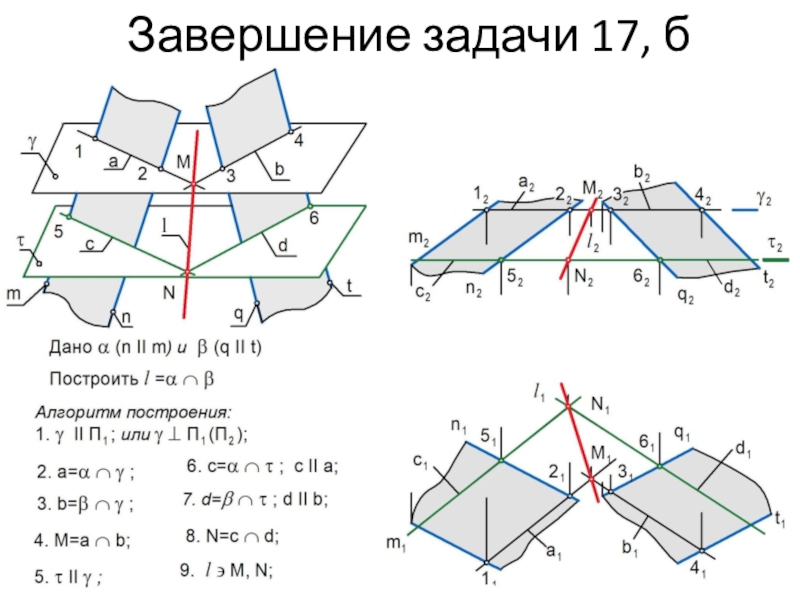
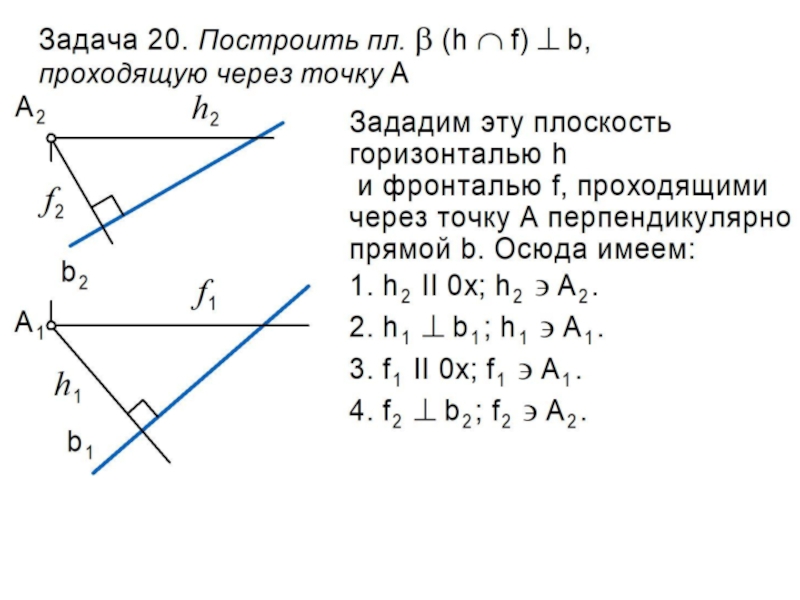
Слайд 22Алгоритм задачи на пересечение двух плоскостей
Задан эпюр двух плоскостей
и .
Необходимо построить их линию пересечения l = .
При
решении задач НГ на пересечение геометрических фигур используют посредники, чаще всего таковыми являются проецирующие плоскости.
1. Строим вспомогательную проецирующую плоскость , которая пересекает плоскость по прямой a , а плоскость – по прямой b. Поскольку обе указанные прямые лежат в плоскости , то пересекаясь они образуют точку М, принадлежащую искомой линии.
2. Для нахождения второй точки N cтроим новую вспомогательную проецирующую плоскость . Далее строим:
с = ; d = ; N = c d.
3. Через точки M и N проводим искомую линию l.
Слайд 23Задача 17,б. Построение линии пересечения двух плоскостей
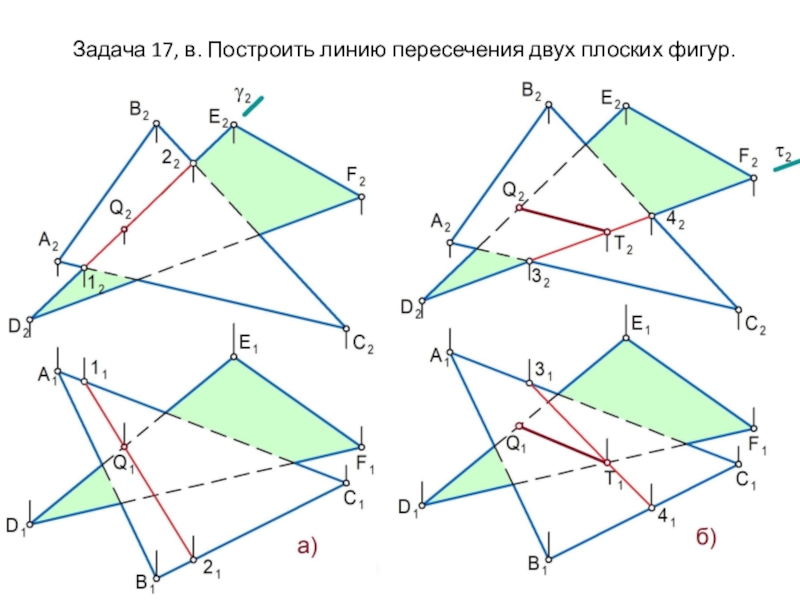
Слайд 25Задача 17, в. Построить линию пересечения двух плоских фигур.
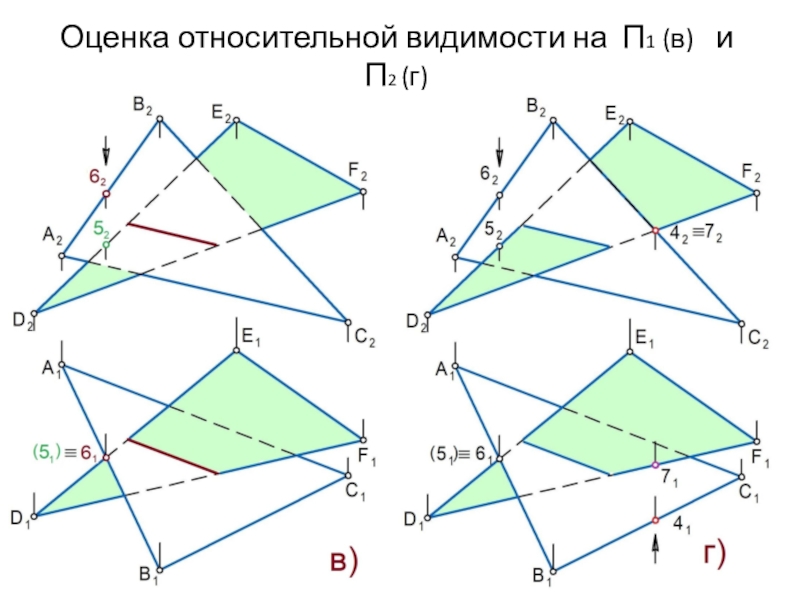
Слайд 26Оценка относительной видимости на П1 (в) и П2 (г)
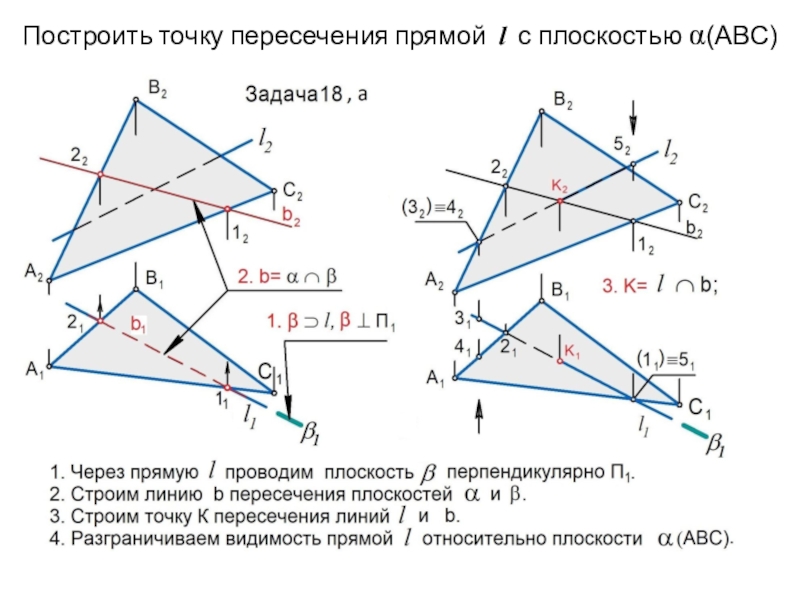
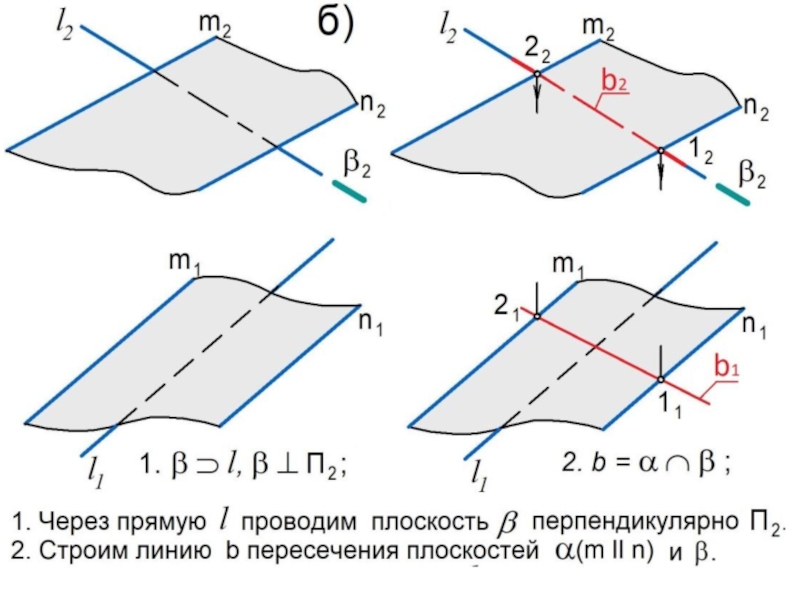
Слайд 27Алгоритм задачи на пересечение прямой и плоскости
Задан эпюр
плоскости общего положения и прямой l .
Необходимо
построить точку К их пересечения: К = l.
1. Через прямую l проводим вспомогательную проецирующую
плоскость .
2. Строим прямую b - линию пересечения плоскостей и :
b = .
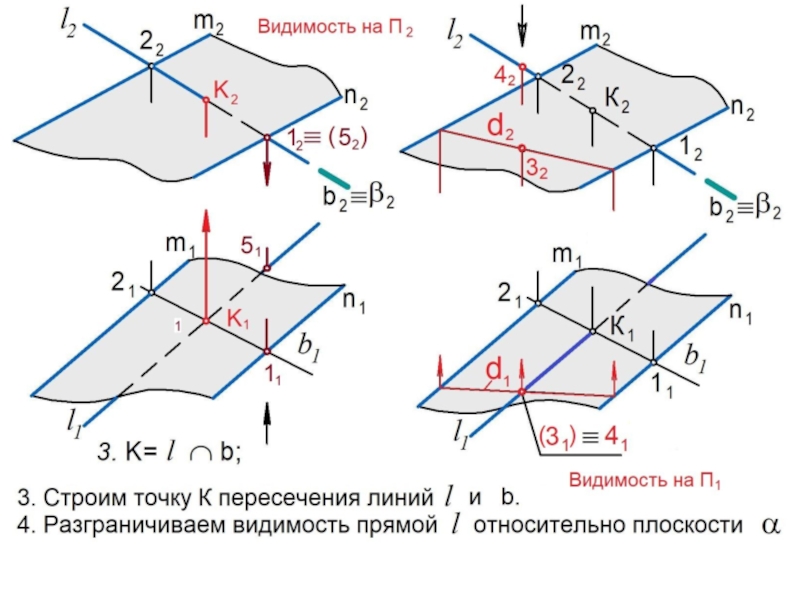
3. Находим искомую точку К, как результат пересечения прямых
l и b: K = l b.
4. Используя конкурирующие точки, разграничиваем видимость
прямой l относительно плоскости .
Слайд 28Построить точку пересечения прямой l с плоскостью (ABC)
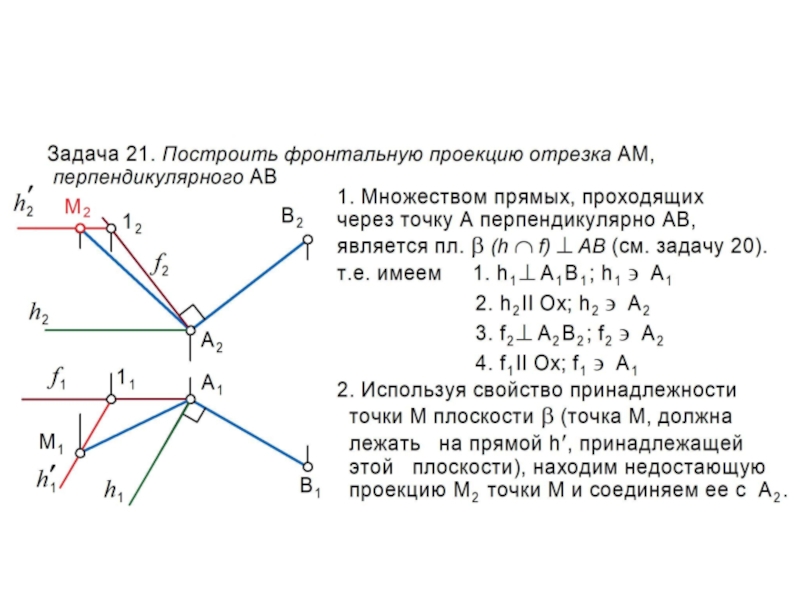
Слайд 31Перпендикуляр к плоскости
Общее геометрическое определение.
Прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым этой плоскости.
Определение для НГ.
Прямая n перпендикулярна плоскости
, если она
одновременно перпендикулярна ее горизонталям h и фронталям f:
n, если а) n h n1 h1;
б) n f n2 f2.
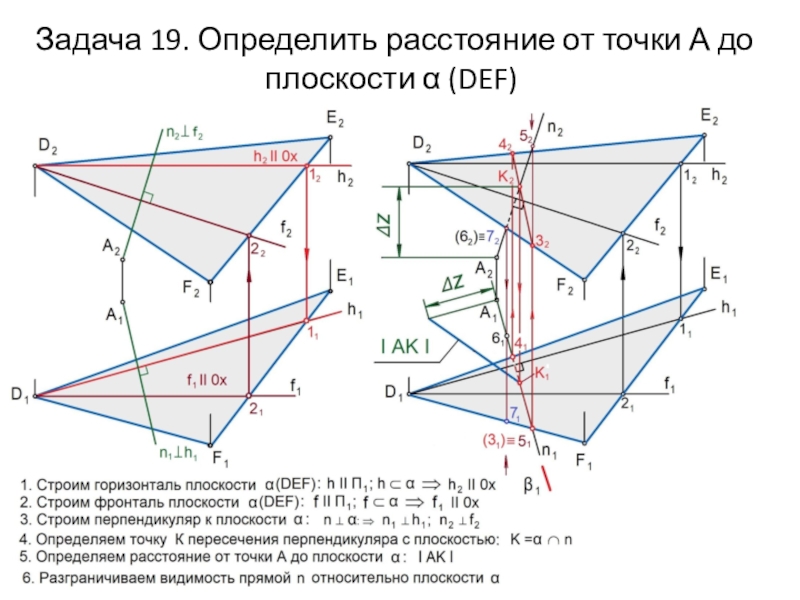
Слайд 32Задача 19. Определить расстояние от точки А до плоскости
(DEF)
Слайд 34Определения взаимно перпендикулярных плоскостей
Определение 1. Две плоскости взаимно перпендикулярны, если
одна из них проходит через перпендикуляр к другой плоскости.
Определение 2.
Две плоскости взаимно перпендикулярны, если одна из них перпендикулярна линии, принадлежащей другой плоскости.