Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 13
Содержание
- 1. РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 13
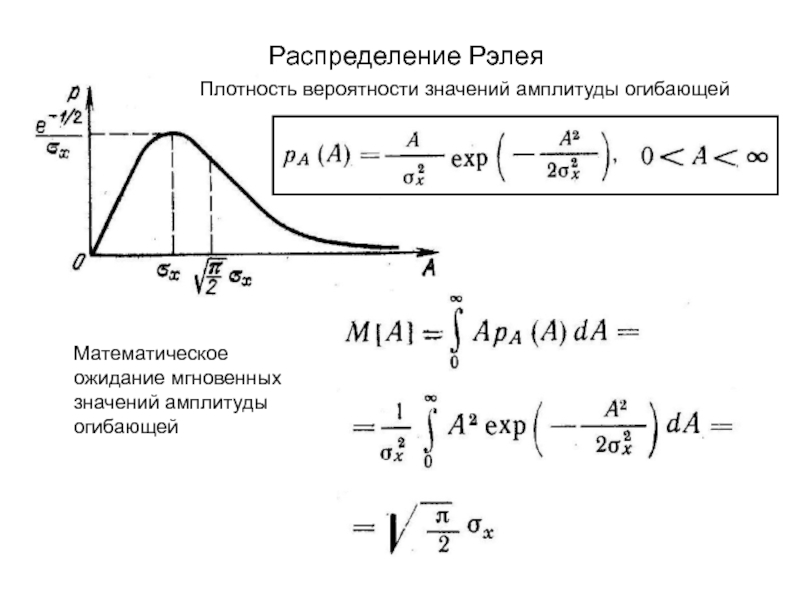
- 2. Распределение РэлеяПлотность вероятности значений амплитуды огибающейМатематическое ожидание мгновенных значений амплитуды огибающей
- 3. Распределение Рэлея
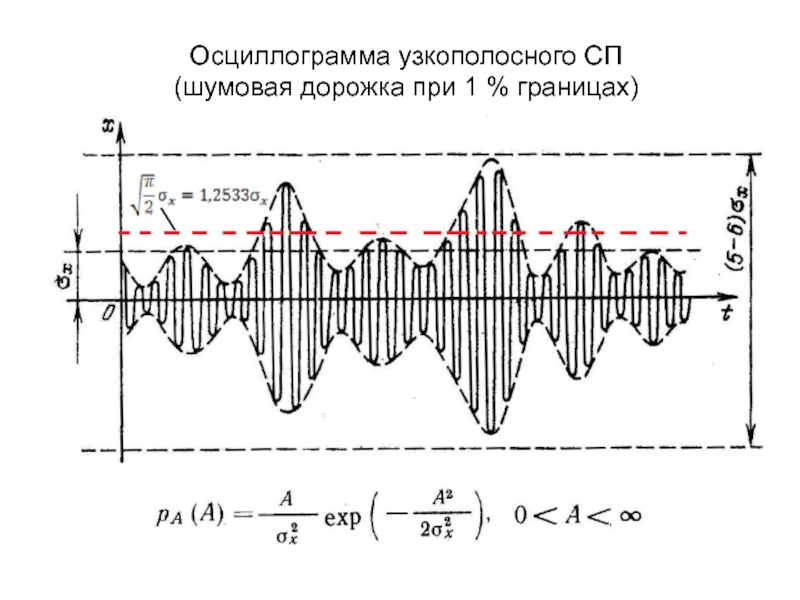
- 4. Осциллограмма узкополосного СП(шумовая дорожка при 1 % границах)
- 5. 8. Огибающая суммы гармонического сигнала и узкополосного
- 6. Огибающая суммы гармонического сигнала и узкополосного нормального
- 7. Огибающая суммы гармонического сигнала и узкополосного нормального
- 8. Огибающая суммы гармонического сигнала и узкополосного нормального
- 9. Графики плотности вероятности случайной величины, распределенной по закону Райса
- 10. Огибающая суммы гармонического сигнала и узкополосного нормального
- 11. Осциллограмма белого шума (No = 1)t = linspace(0,1e-3, 2^16);In = randn(1, 2^16);plot(t, In)t
- 12. Осциллограмма суммы гармоники и белого шума (Uo=1)f0 =1e4;wo = 2*pi*f0;Uo= 1;Is = Uo*sin(wo*t);plot(t, [(Is+In)‘ Is'])t
- 13. Осциллограмма огибающей (Uo=1)Qn = randn(1,2^16);Qs = Uo*cos(w0*t);sn = Qs+Qn+j*(Is+In);Asn = abs(sn);plot(t,Asn)t
- 14. Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n
- 15. Осциллограмма суммы гармоники и белого шума (Uo=3)f0
- 16. Осциллограмма огибающей (Uo=3)Qn = randn(1,2^16);Qs = Uo*cos(w0*t);sn = Qs+Qn+j*(Is+In);Asn = abs(sn);plot(t,Asn)t
- 17. Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n
- 18. 8.2. Интервал корреляции Числовой характеристикой, служащей
- 19. 8.3. Эффективная ширина спектра
- 20. ПримерЗдесь высокочастотный сомножитель имеет период 106 с,
- 21. 8.4. Белый шумВ радиотехнике так принято называть
- 22. Белый шум Средняя мощность
- 23. 8.5. Дифференцирование и интегрирование случайных процессовДифференциальные свойства
- 24. Дифференцирование случайных процессовПусть математическое ожидание исходного процесса
- 25. Дифференцирование случайных процессовВсе четыре слагаемых в квадратных
- 26. 8.6. Дифференцируемые и недифференцируемые случайные процессы
- 27. Дифференцируемые и недифференцируемые случайные процессы
- 28. 8.7. Спектральная плотность мощности производной
- 29. 8.8. Корреляционная связь между случайным процессом и
- 30. Корреляционная связь между случайным процессом и его
- 31. 8.9. Интеграл от случайного процесса
- 32. Интеграл от случайного процесса Однако
- 33. Интеграл от случайного процесса
- 34. Сумма от случайного процесса с равномерным распределениемR = rand(10,100);W = cumsum( (R - 0.5)‘ );plot(W)
- 35. Реализации винеровского процесса(суммы нормального белого шума )N = randn(10,100);Wn = cumsum( (N)‘ );plot(Wn)
- 36. 8.10. Шумоподобный сигнал В
- 37. Шумоподобный сигнал Шумоподобные сигналы
- 38. Формирование шумоподобного сигнала Для формирования
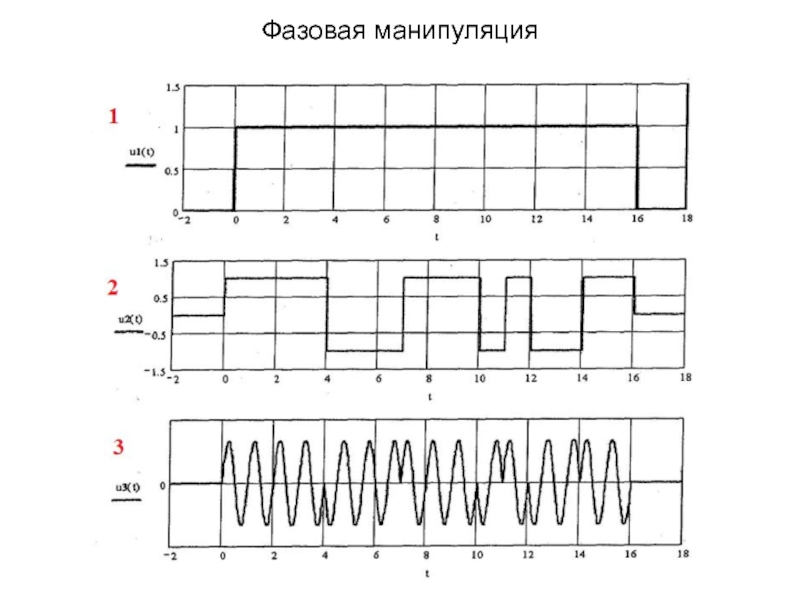
- 39. Фазовая манипуляция
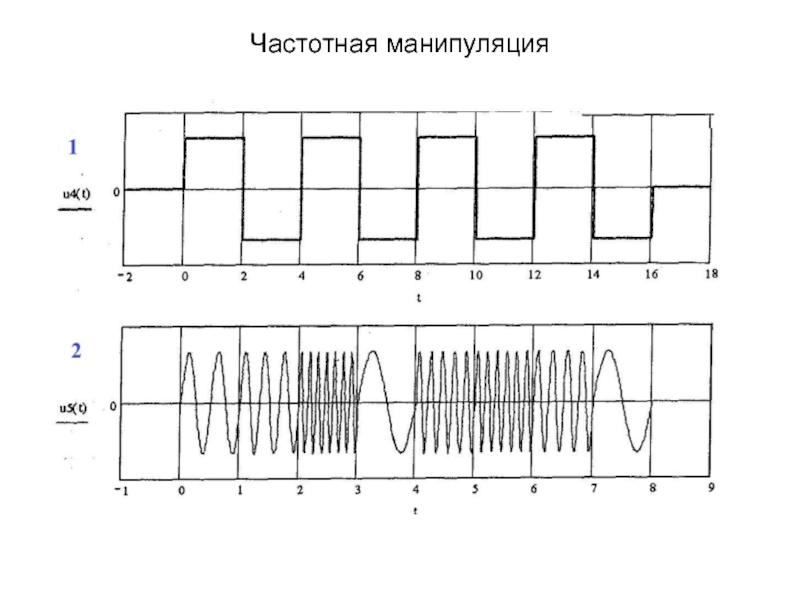
- 40. Частотная манипуляция
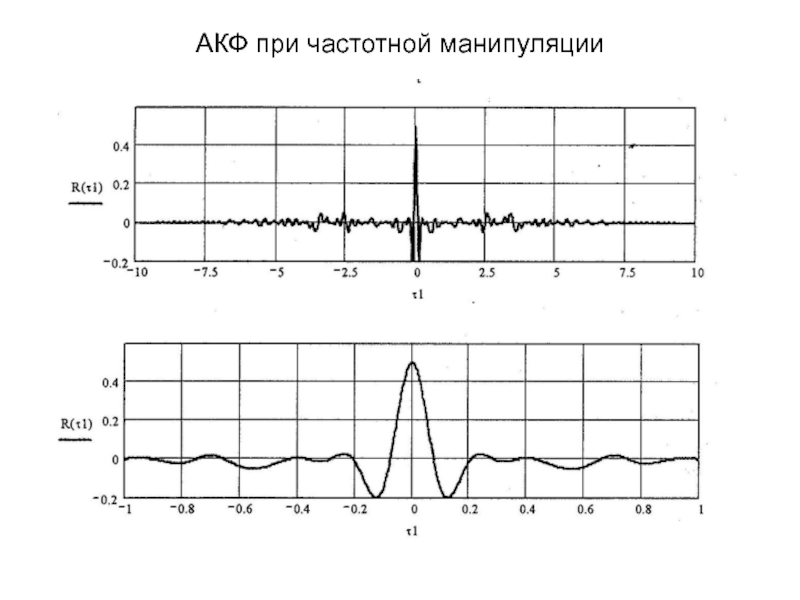
- 41. АКФ при частотной манипуляции
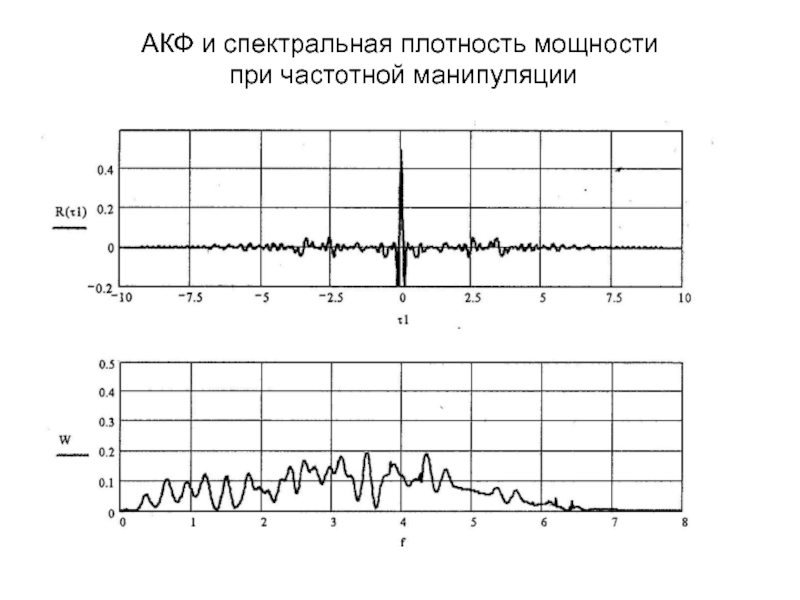
- 42. АКФ и спектральная плотность мощности при частотной манипуляции
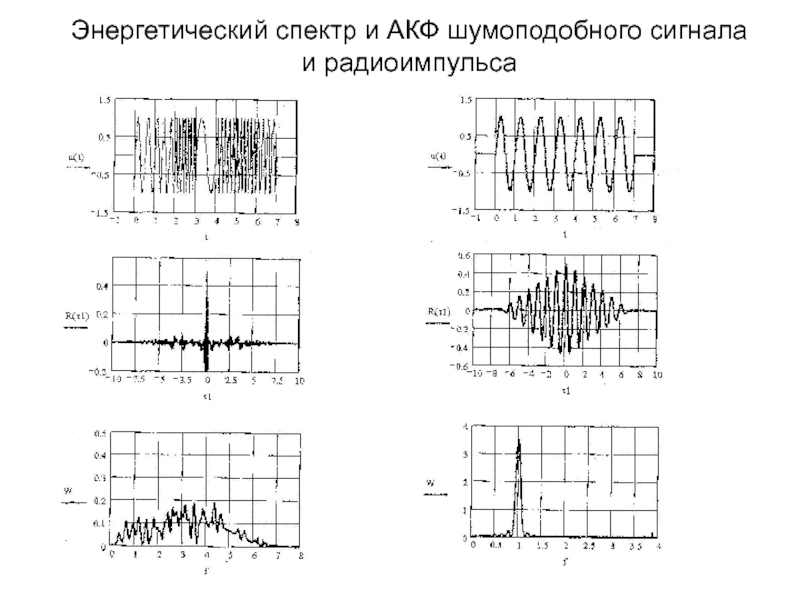
- 43. Энергетический спектр и АКФ шумоподобного сигналаи радиоимпульса
- 44. Благодарю за внимание!
- 45. Скачать презентанцию
Слайды и текст этой презентации
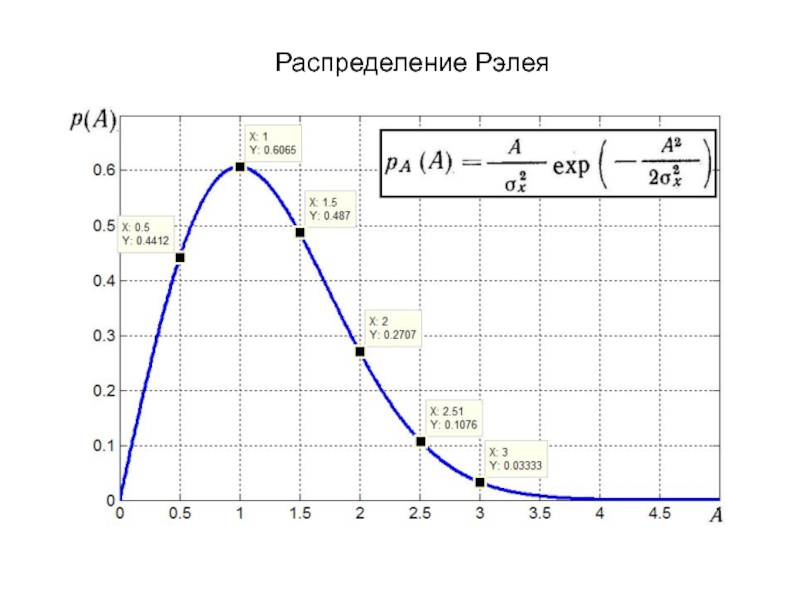
Слайд 2Распределение Рэлея
Плотность вероятности значений амплитуды огибающей
Математическое ожидание мгновенных значений амплитуды
огибающей
Слайд 58. Огибающая суммы гармонического сигнала и узкополосного нормального шума
В радиотехнике часто интересуются статистическими свойствами сигнала, наблюдаемого на
выходе некоторого частотно-избирательного устройства, например, резонансного усилителя. Будем считать, что помимо флуктуа-ционного гауссова шума с центральной частотой , равной резонансной частоте усилителя, на выходе присутствует также детерминированный гармонический сигнал с известной амплитудой Um.Определим одномерную функцию плотности вероятности огибающей суммарного колебания. Считая, что полезный сигнал s(t) = Um cos( t), в то время как шум, запишем выражение реализации суммарного процесса:
Данный случайный процесс узкополосен, поэтому его реализация может быть выражена посредством медленно меняющихся огибающей U(t) и начальной фазы :
Слайд 6
Огибающая суммы гармонического сигнала и узкополосного нормального шума
Очевидно, между парами
имеется связь:
Якобиан D этого преобразования равен U. Тогда, поскольку двумерная плотность вероятности
в новых переменных имеем
Слайд 7
Огибающая суммы гармонического сигнала и узкополосного нормального шума
Проинтегрируем правую часть
формулы по угловой координате:
в результате чего находим
Данная формула выражает закон,
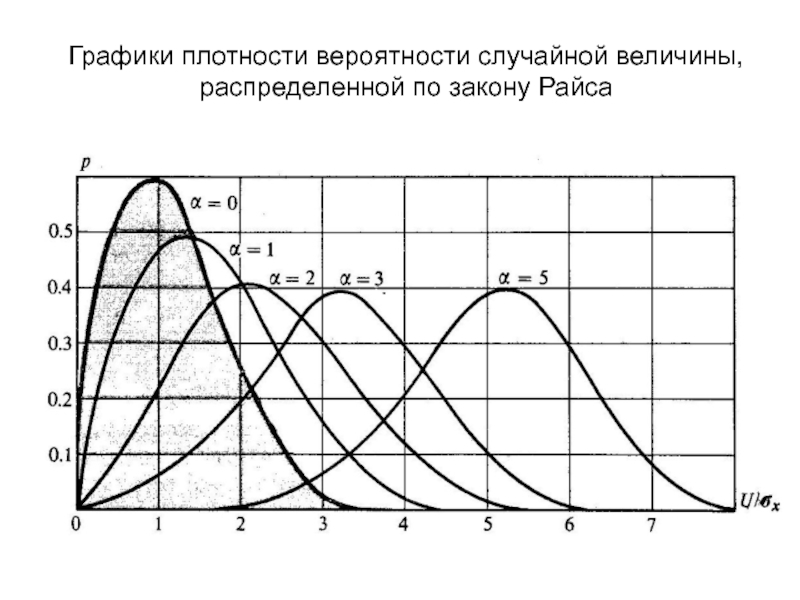
получивший в радиотехнике название закона Райса. Отметим, что при Um = 0, т. е. в отсутствие детерминированного сигнала, закон Райса переходит в закон Рэлея.Слайд 8
Огибающая суммы гармонического сигнала и узкополосного нормального шума
Ниже представлены графики
плотности вероятности случайной величины, распределенной по закону Райса при различных
отношениях.
Отметим, что если амплитуда детерминированного сигнала значительно превышает среднеквадратический уровень шума, т. е. то при можно воспользоваться асимптотическим представлением модифицированных функций Бесселя с большим аргументом:
После подстановки его в исходное соотношение, имеем
т.е. огибающая результирующего сигнала распределена в этом случае приближенно нормально с дисперсией и математическим ожиданием
Слайд 10
Огибающая суммы гармонического сигнала и узкополосного нормального шума
Практически считают, что
уже при
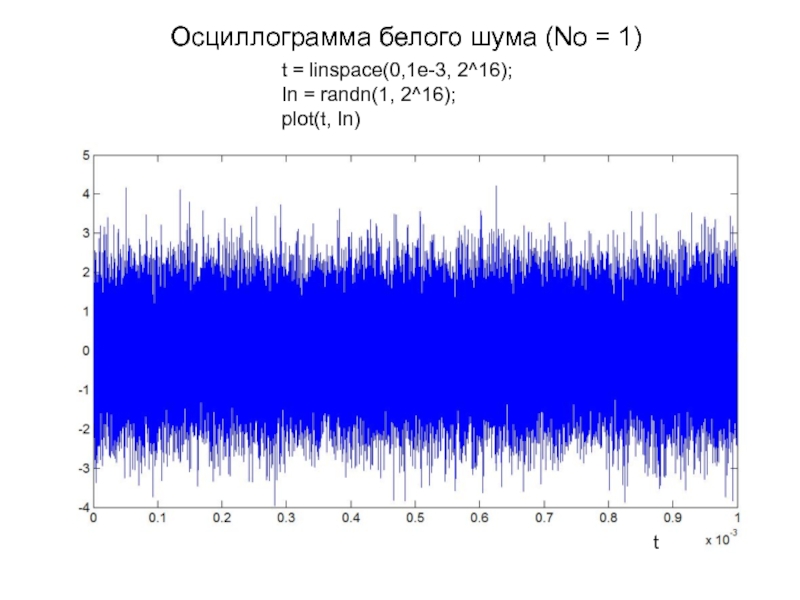
огибающая результирующего сигнала нормализуется. Полезно вспомнить, что огибающая чистого шума, распределенная по закону Рэлея, имеет дисперсию, равную Таким образом, наложение достаточно большого гармонического сигнала приводит более чем к двукратному росту дисперсии огибающей ( ). Тем не менее относительные флуктуации огибающей при этом падают. Действительно, для чистого шума величина которую удобно принять в качестве числовой оценки флуктуации, равна 0.523. При большом детер-мированном сигнале величина стремясь к нулю с ростом амплитудыСлайд 11Осциллограмма белого шума (No = 1)
t = linspace(0,1e-3, 2^16);
In =
randn(1, 2^16);
plot(t, In)
t
Слайд 12Осциллограмма суммы гармоники и белого шума (Uo=1)
f0 =1e4;
wo = 2*pi*f0;
Uo=
1;
Is = Uo*sin(wo*t);
plot(t, [(Is+In)‘ Is'])
t
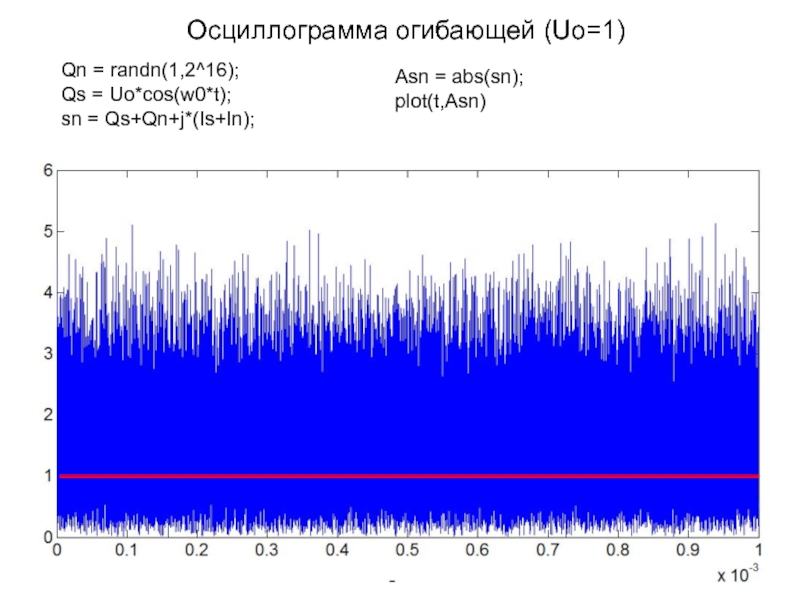
Слайд 13Осциллограмма огибающей (Uo=1)
Qn = randn(1,2^16);
Qs = Uo*cos(w0*t);
sn = Qs+Qn+j*(Is+In);
Asn =
abs(sn);
plot(t,Asn)
t
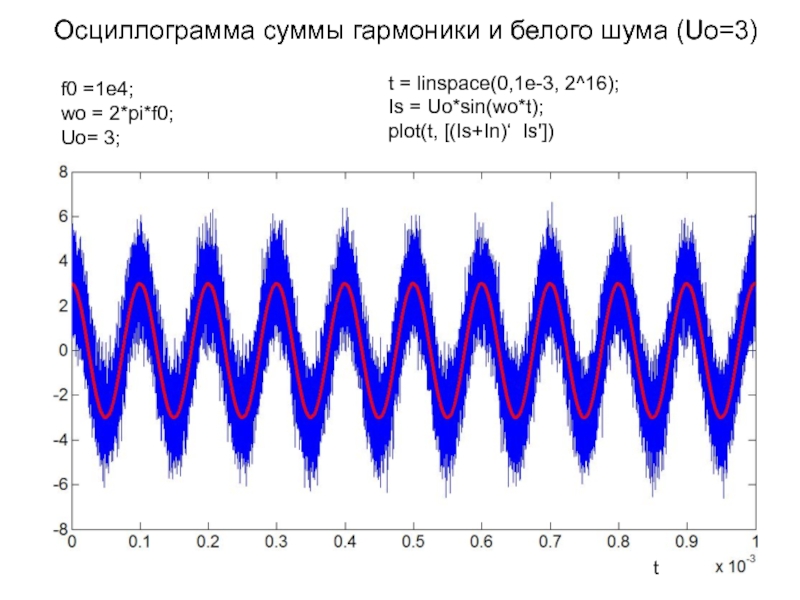
Слайд 15Осциллограмма суммы гармоники и белого шума (Uo=3)
f0 =1e4;
wo = 2*pi*f0;
Uo=
3;
t = linspace(0,1e-3, 2^16);
Is = Uo*sin(wo*t);
plot(t, [(Is+In)‘ Is'])
t
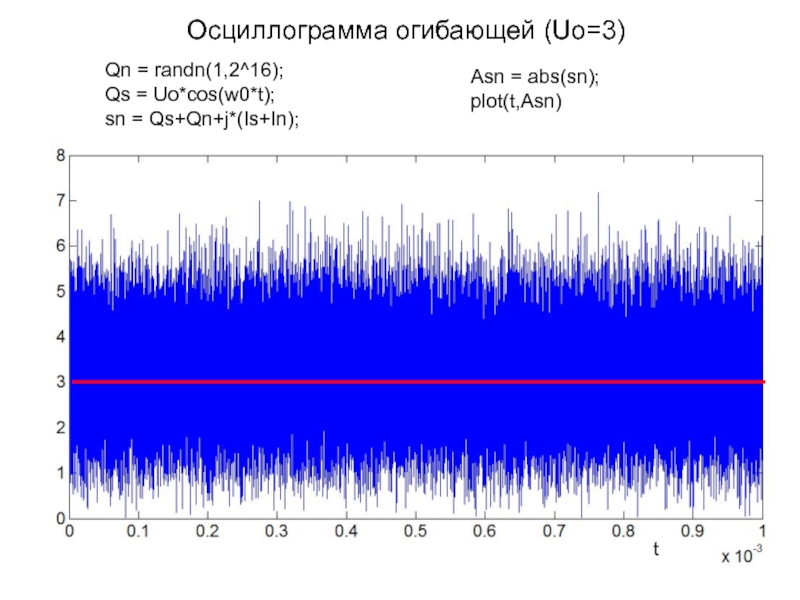
Слайд 16Осциллограмма огибающей (Uo=3)
Qn = randn(1,2^16);
Qs = Uo*cos(w0*t);
sn = Qs+Qn+j*(Is+In);
Asn =
abs(sn);
plot(t,Asn)
t
Слайд 188.2. Интервал корреляции
Числовой характеристикой, служащей для оценки «скорости
изменения» реализаций случайного процесса, является интервал корреляции определяемый выражением
Если известна
информация о поведении какой-либо реализации «в прошлом», то возможен вероятностный прогноз случайного процесса на время порядка . Однако попытка прогнозирования на время, существенно превышающее интервал корреляции, окажется безрезультатной – мгновенные значения, столь далеко отстоящие во времени, практически некоррелированы, т. е. среднее значение произведения стремится к нулю.Слайд 198.3. Эффективная ширина спектра
Пусть исследуемый
случайный процесс характеризуется функцией -
односторонним спектром мощности, причем — экстремальное значение этой функции. Заменим этот случайный процесс другим процессом, у которого спектральная плотность мощности постоянна и равна в пределах эффективной полосы частот , выбираемой из условия равенства средних мощностей обоих процессов:Отсюда получается формула для эффективной ширины спектра:
Этой числовой характеристикой часто пользуются для инженерного расчета дисперсии шумового сигнала: .
Например, если известно, что
откуда среднеквадратическое значение напряжения шума
Слайд 20Пример
Здесь высокочастотный сомножитель имеет период 106 с, амплитудный сомножитель изменяется
за это время лишь в ехр(-10 --2) = 0.99 раза.
Поэтому рассматриваемый случайный процесс можно считать узкополосным с центральной частотой fо = 1 МГц. Ограничиваясь первым членом ряда в формуле определения АКФ огибающей и заменяя приближенно коэффициент 0.915 на единицу, находим нормированную функцию корреляции огибающей:Дисперсия огибающей , откуда функция корреляции
Интервал корреляции огибающей
составляет 50 периодов гармонического колебания с частотой fо. Наконец, односторонний спектр мощности огибающей
имеет низкочастотный характер ( = 3.11e4 рад/с).
Функция корреляции некоторого случайного процесса (В2)
Слайд 218.4. Белый шум
В радиотехнике так принято называть стационарный случайный процесс
с постоянной на всех частотах спектральной плотностью мощности:
Термин «белый шум»
образно подчеркивает аналогию с «белым» (естественным) светом, у которого в пределах видимого диапазона интенсивность всех спектральных составляющих приблизительно одинакова.По теореме Винера - Хинчина функция корреляции белого шума
равна нулю всюду, кроме точки т = 0.
Слайд 22Белый шум
Средняя мощность (дисперсия) белого шума
неограниченно велика.
Белый шум является дельта-коррелированным случайным процессом. Некоррелированность мгновенных значений
такого случайного сигнала означает бесконечно большую скорость изменения их во времени - как бы мал ни был интервал , сигнал за это время может измениться на любую наперед заданную величину.Белый шум является абстрактной математической моделью и отвечающий ему физический процесс в природе, безусловно, не существует. Однако это не мешает приближенно заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.
Слайд 238.5. Дифференцирование и интегрирование
случайных процессов
Дифференциальные свойства случайного процесса определяются
видом его функции корреляции.
Предположим, что реализация х(t) случайного процесса X(t)
подается на дифференцирующее устройство, создающее на выходе новую реализацию у(t) = dx/dt. Совокупность реализаций у(t) образует случайный процесс Y(t), называемый производной процесса X(t). Символически этот факт обозначается равенствомПоложим, что X(t) - стационарный случайный процесс с известным математическим ожиданием х. Чтобы найти математическое ожидание производной, проведем усреднение по ансамблю реализаций:
При дифференцировании стационарного случайного процесса возникает новый случайный процесс с нулевым математическим ожиданием.
Слайд 24Дифференцирование случайных процессов
Пусть математическое ожидание исходного процесса
(если это не так, то
всегда можно перейти к новому процессу Z(t), реализации которого z(t) = x(t) - mx). Воспользуемся тем, чтои представим функцию корреляции производной таким образом:
Слайд 25Дифференцирование случайных процессов
Все четыре слагаемых в квадратных скобках представляют собой
функции корреляции исходного процесса, вычисленные при различных величинах задержки:
Правая часть
последнего равенства представляет собой вторую производную функции Rx(т), взятую с обратным знаком:Слайд 268.6. Дифференцируемые и недифференцируемые случайные процессы
По определению,
случайный процесс X(t) является дифференцируемым, если его производная имеет конечную
дисперсию. Дисперсия производнойПоэтому для дифференцируемости случайного процесса необходимо, чтобы вторая производная его функции корреляции в нуле была конечной величиной, а значит, первая производная этой функции в нуле - непрерывной.
Недифференцируемым является случайный процесс с функцией корреляции вида
Дифференцируя эту функцию один раз, убеждаемся, что производная в нуле изменяется скачком на величину
В радиотехнике часто рассматривают случайные процессы с функциями корреляции вида
Простое вычисление показывает, что. первая производная этой функции
в нуле непрерывна, поэтому такая функция корреляции отвечает дифференцируемому процессу.
Слайд 27Дифференцируемые и недифференцируемые случайные процессы
Реализации любых случайных
сигналов, с которыми приходится встречаться в технике, всегда достаточно «гладкие»
для того, чтобы быть дифференцируемыми. Однако в теоретических исследованиях часто возникают математические модели, соответствующие недифференцируе-мым процессам. Как правило, это имеет место тогда, когда реализации случайного процесса образуются из очень большого числа малых независимых слагаемых. Несмотря на то что вклад одного такого слагаемого (например, импульса тока от движения отдельно взятого электрона) ничтожен, именно эти слагаемые определяют «тонкую структуру» реализации. Как следствие, реализации такого процесса могут приобрести вид функции, всюду непрерывной, однако ни в одной точке не дифференцируемой.Слайд 288.7. Спектральная плотность мощности производной
Найдем связь между
спектрами мощности исходного процесса и его производной. Пусть задано соответствие
По теореме Винера- Хинчина функция корреляции исходного процессаФункция корреляции производной
откуда получается искомая формула связи
Примечательно, что в спектре мощности производной наблюдается уменьшение низких и увеличение высоких частот. Случайный процесс дифференцируем, если
Слайд 298.8. Корреляционная связь между случайным процессом
и его производной
Во многих задачах статистической радиотехники существен вопрос вероятностной
связи между мгновенными значениями случайного сигнала и его производной. Для ответа на него вычислим функцию взаимной корреляции случайных процессов и проведя усреднение:откуда
Принято во внимание, что оба рассматриваемых случайных процесса стационарны и имеют нулевые средние значения.
Слайд 30Корреляционная связь между случайным процессом
и его производной
Как известно, функция Rx(т) всегда является четной. Если же процесс
дифференцируем, то при т = 0 производная R'x (т) обращается в нуль. Отсюда следует, что мгновенные значения такого случайного сигнала и его производной, взятые в один и тот же момент времени, являются некоррелированными. Еще более сильное утверждение справедливо применительно к гауссовым случайным процессам: здесь случайный сигнал и его производная статистически независимы.Слайд 318.9. Интеграл от случайного процесса
Будем называть
случайный процесс Z(t) определенным интегралом с переменным верхним пределом от
случайного процесса X(t), если между реализациями z(t) и х(t) имеется соответствие видаФизически это означает, что сигналы z(t) наблюдаются на выходе идеального интегратора, причем входные сигналы х(t) начинают поступать в нулевой момент времени. Если процесс X(t) стационарен и имеет постоянное среднее значение то математическое ожидание сигнала на выходе интегратора
Таким образом, условие сразу приводит к нестационарности случайного процесса Z(t).
Слайд 32Интеграл от случайного процесса
Однако даже при нулевом
математическом ожидании входного процесса сигнал на выходе интегратора будет представлять
собой реализацию нестационарного случайного процесса. Чтобы убедиться в этом, вычислим функцию корреляции интеграла:Если процесс X(t) стационарен, то аргумент функции корреляции, стоящей под знаком интеграла в последней формуле, будет представлять собой разность поэтому
Поскольку правая часть формулы зависит непосредственно от t1 и t2, а не от их разности, случайный процесс на выходе интегратора является нестационарным.
Слайд 33Интеграл от случайного процесса
Нестационарность интеграла от
случайного процесса имеет глубокий физический смысл, свидетельствуя о безграничном нарастании
флуктуации на выходе идеального интегратора, что связано с эффектом их накопления.Сходные задачи часто встречаются в различных областях физики. В качестве примера можно привести известную проблему одномерного случайного блуждания точки (броуновского движения). Здесь материальная точка, выходя из начала координат и получая равновероятные толчки в двух противоположных направлениях, в среднем остается на месте, однако величина ее отклонения от среднего положения неограниченно нарастает во времени прямо пропорционально корню квадратному от текущего времени.
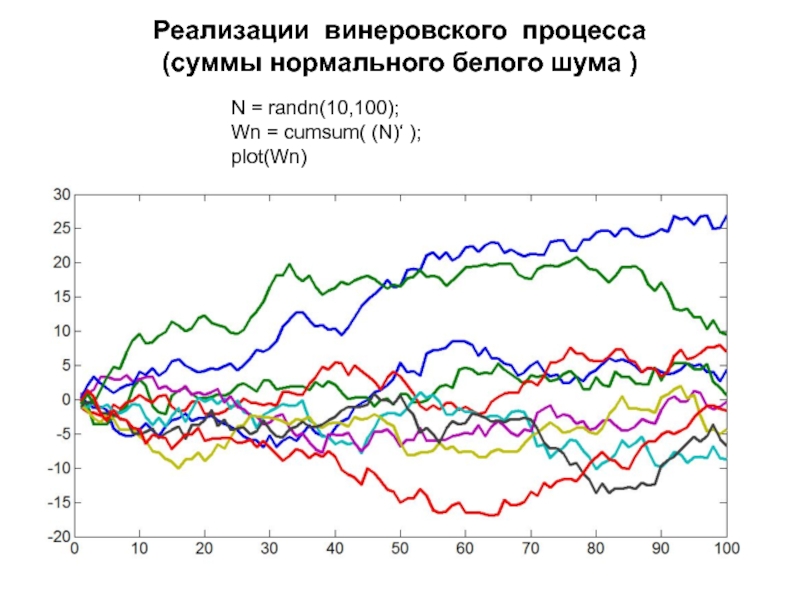
Нестационарный случайный процесс, получаемый путем интегрирования белого шума, принято называть случайным процессом Винера.
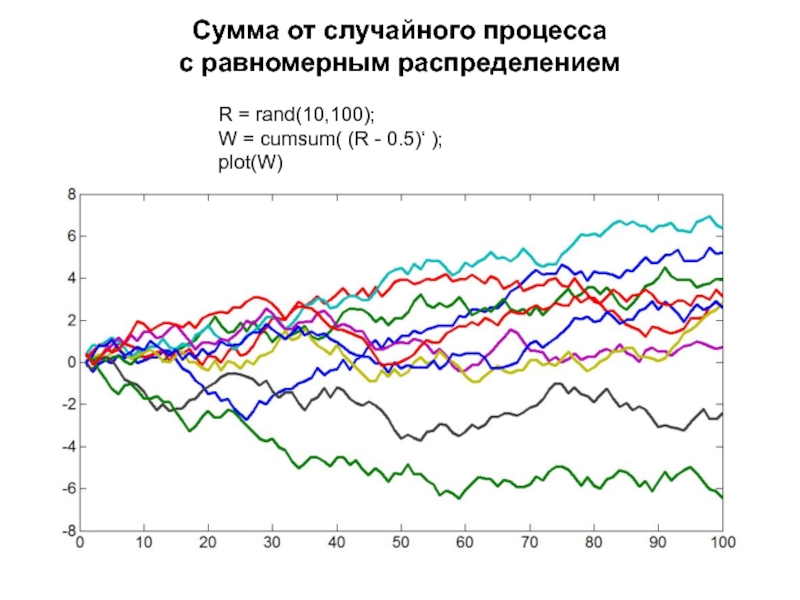
Слайд 34Сумма от случайного процесса
с равномерным распределением
R = rand(10,100);
W =
cumsum( (R - 0.5)‘ );
plot(W)
Слайд 35Реализации винеровского процесса
(суммы нормального белого шума )
N = randn(10,100);
Wn =
cumsum( (N)‘ );
plot(Wn)
Слайд 368.10. Шумоподобный сигнал
В радиотехнике помимо узкополосных
повсеместное применение находят и широкополосные сигналы. К числу последних относятся,
в частности, шумоподобные сигналы, получившие такое название по причине близости их спектра к белому шуму. Шумоподобный сигнал имеет ширину спектра во много раз превышающую данную величину у передаваемого сообщения, что оценивается с помощью базы сигнала В.Отметим три особенности шумоподобного сигнала.
1. Он имеет значение базы сигнала B >> 1, достигая в некоторых случаях нескольких тысяч. Напомним, что база сигнала показывает, во сколько раз ширина спектра модулированного высокочастотного колебания возрастает по сравнению с данным параметром модулирующего сигнала.
2. При формировании шумоподобного сигнала используется фактор псевдослучайности, благодаря чему по своей структуре он становится близким к случайному сигналу.
3. Распознать шумоподобный сигнал при приеме можно, только зная «ключ» кодирования при передаче, что обеспечивает скрытность связи.
Слайд 37Шумоподобный сигнал
Шумоподобные сигналы используются:
– при кодовой
адресации большого числа абонентов и их кодовом раз делении в системах
множественного доступа к относительно широ кополосному каналу радиосвязи;– для повышения помехозащищенности радиотехнических систем от действия мощных помех преднамеренного характера;
– для обеспечения скрытности передаваемого сообщения и защиты от несанкционированного приема;
– для борьбы с многолучевостью, связанной с одновременным приёмом сигналов нескольких радиолучей – основного и отраженных от ионосферы или каких-либо препятствий и потому пришедших с задержкой по времени;
– при измерении дальности и скорости движения объектов в системах радиолокации и радионавигации.






![РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 13 Осциллограмма суммы гармоники и белого шума (Uo=1)f0 =1e4;wo = 2*pi*f0;Uo= 1;Is = Uo*sin(wo*t);plot(t, [(Is+In)‘ Is'])t Осциллограмма суммы гармоники и белого шума (Uo=1)f0 =1e4;wo = 2*pi*f0;Uo= 1;Is = Uo*sin(wo*t);plot(t, [(Is+In)‘ Is'])t](/img/thumbs/c76da1e4c103b8b120bec02b6f21f680-800x.jpg)
![РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 13 Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n](/img/thumbs/8086148f9a2022393229663fff6aeb52-800x.jpg)
![РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 13 Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n Гистограмма огибающей суммы гармоники и белого шума[n,x] = hist(Asn,50);bar(x, n/2^16)S+n](/img/thumbs/eb8f699980bb70b2a6b9664b3828bb6e-800x.jpg)