Слайд 1РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
И СИГНАЛЫ
Лекционный курс
Лекция 16
Доцент Трухин М.П.
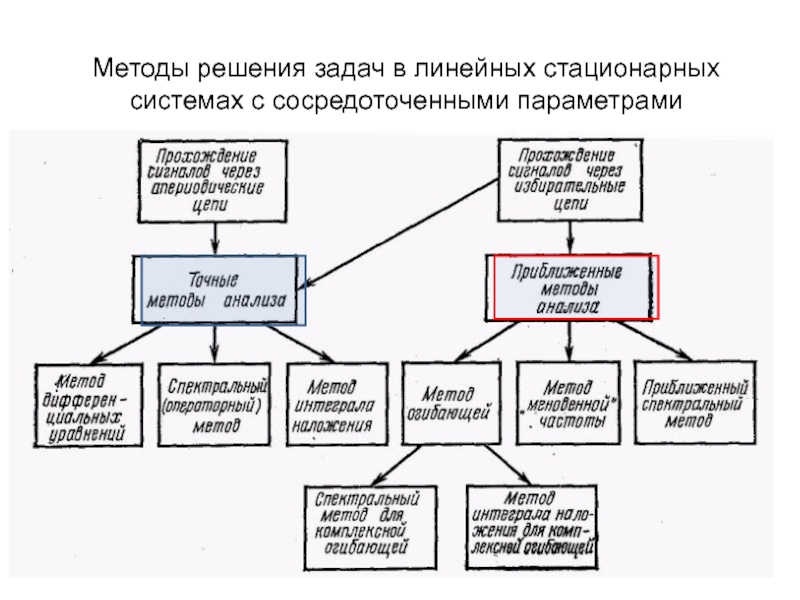
Слайд 2Методы решения задач в линейных стационарных системах с сосредоточенными параметрами
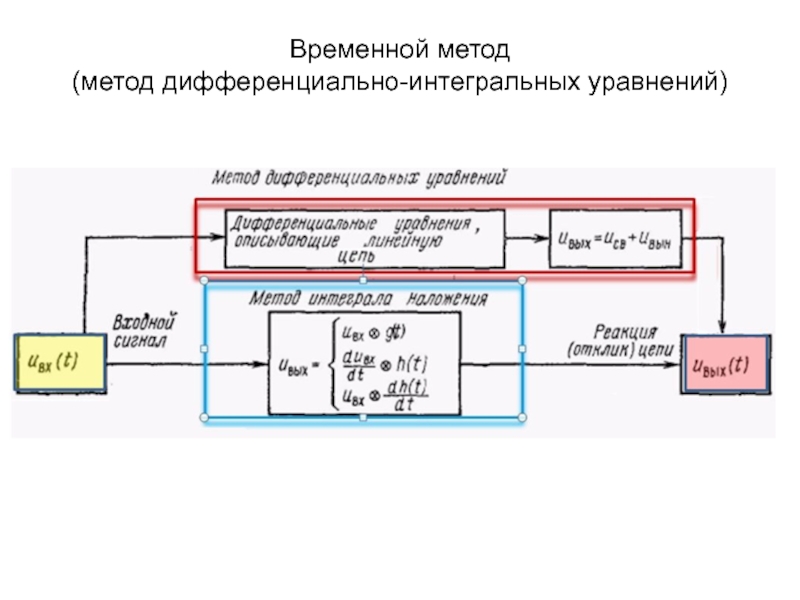
Слайд 3Временной метод
(метод дифференциально-интегральных уравнений)
Слайд 4Импульсная характеристика
Пусть некоторая линейная стационарная система описывается оператором Т. Для
простоты будем полагать, что входной и выходной сигналы одномерны. По
определению, импульсной характеристикой системы h(t) называется функция являющаяся откликом системы на входной сигнал Это означает, что функция h(t) удовлетворяет уравнению
Поскольку система стационарна, аналогичное уравнение
будет и в случае, если входное воздействие смещено во времени на производную величину:
Слайд 5Импульсная характеристика
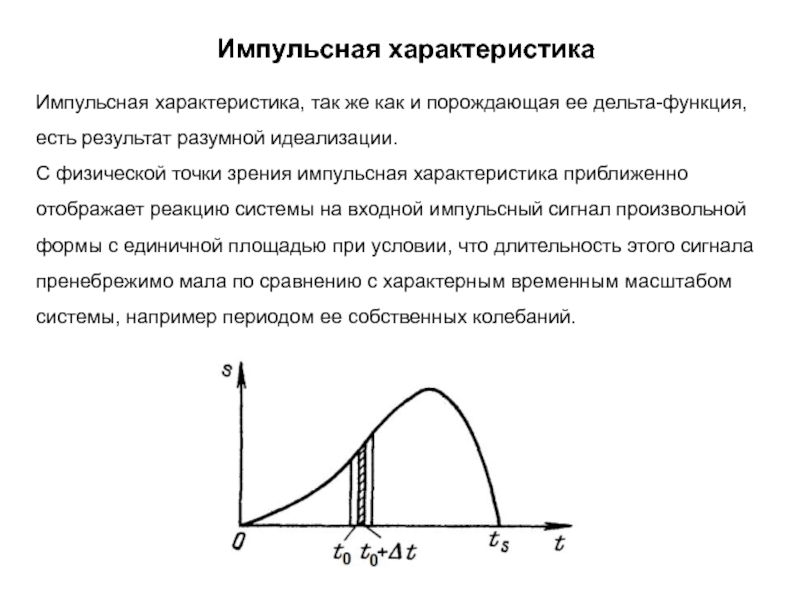
Импульсная характеристика, так же как и порождающая ее дельта-функция,
есть результат разумной идеализации.
С физической точки зрения импульсная характеристика
приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например периодом ее собственных колебаний.
Слайд 6Интеграл Дюамеля
Зная импульсную характеристику линейной стационарной системы, можно формально решить
любую задачу о прохождении детерминированного сигнала через такую систему. Поскольку
входной сигнал всегда допускает представление вида
то отвечающая ему выходная реакция будет определяться интегральным соотношением
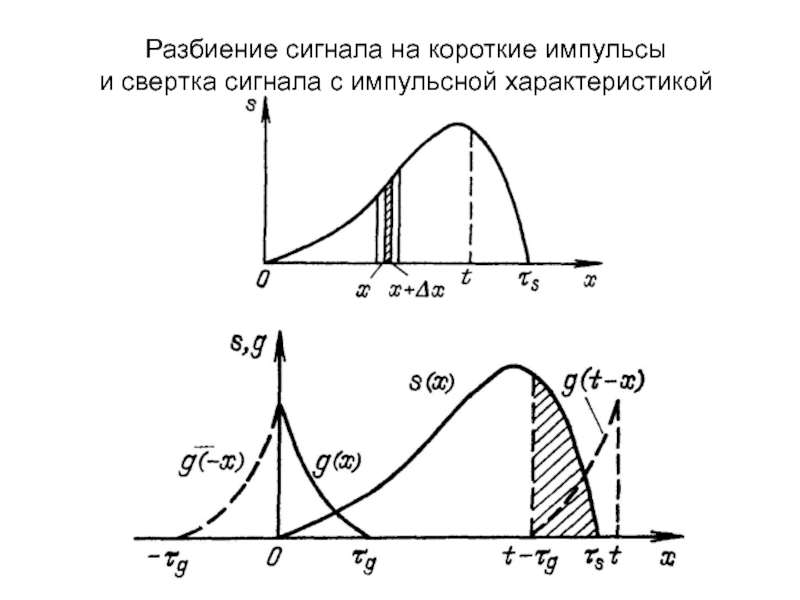
Слайд 7Разбиение сигнала на короткие импульсы
и свертка сигнала с импульсной
характеристикой
Слайд 8Интеграл Дюамеля
Интеграл есть предельное значение суммы, поэтому линейный оператор Т
на основании принципа суперпозиции может быть внесен под знак интеграла.
Далее, оператор Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования . Поэтому
или окончательно
Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля. Выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы. Она может быть записана также в виде
Первая форма
Слайд 9Интеграл Дюамеля
Итак, если импульсная характеристика h(t) известна, то дальнейшие
этапы решения сводятся к полностью формализованным операциям.
Вторая форма
В математике импульсную
характеристику называют функцией Грина рассматриваемого оператора Т.
Импульсную характеристику следует рассматривать, строго говоря, как обобщенную функцию.
Слайд 10Пример 1
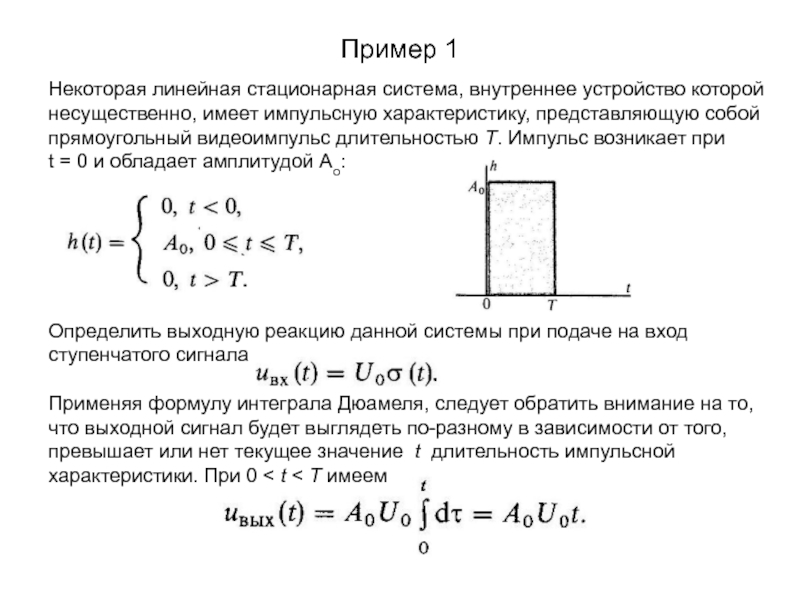
Некоторая линейная стационарная система, внутреннее устройство которой несущественно,
имеет импульсную характеристику, представляющую собой прямоугольный видеоимпульс длительностью Т. Импульс
возникает при
t = 0 и обладает амплитудой Ао:
Определить выходную реакцию данной системы при подаче на вход ступенчатого сигнала
Применяя формулу интеграла Дюамеля, следует обратить внимание на то, что выходной сигнал будет выглядеть по-разному в зависимости от того, превышает или нет текущее значение t длительность импульсной характеристики. При 0 < t < Т имеем
Слайд 11Пример 1. Продолжение
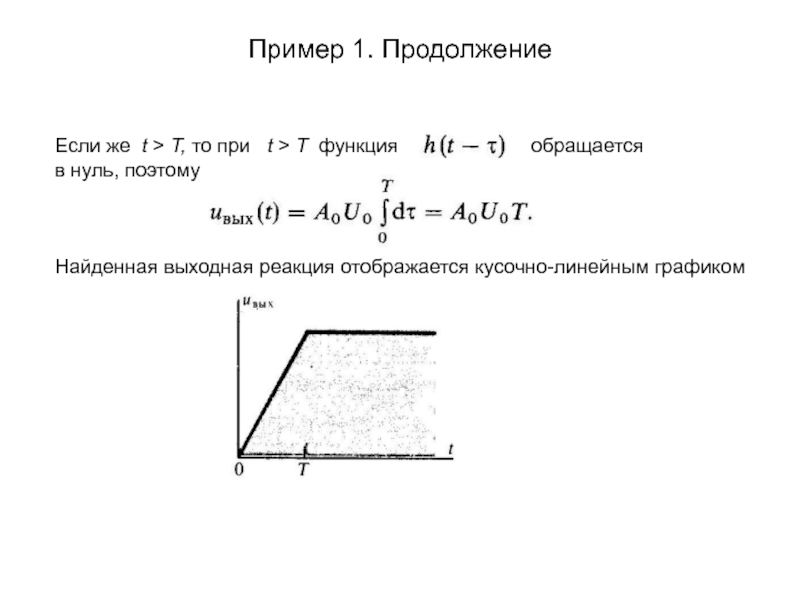
Если же t > Т, то при
t > Т функция
обращается в нуль, поэтому
Найденная выходная реакция отображается кусочно-линейным графиком
Слайд 12Пример 2
На вход интегрирующей RC-цепи подаётся радиоимпульс
clear all
R=1;
C=0.5;
F=1;
N=1024;
T=8;
dt=T/(N-1);
Fd=1/dt;
tau=R*C;
tau1=1/(R*C);
t1=linspace(0,T,N);
s=[2*cos(2*pi*F*t1) zeros(1,N)];
t=linspace(0,2*T,2*N);
figure(1)
plot(t,s)
Слайд 13Пример 2. Продолжение
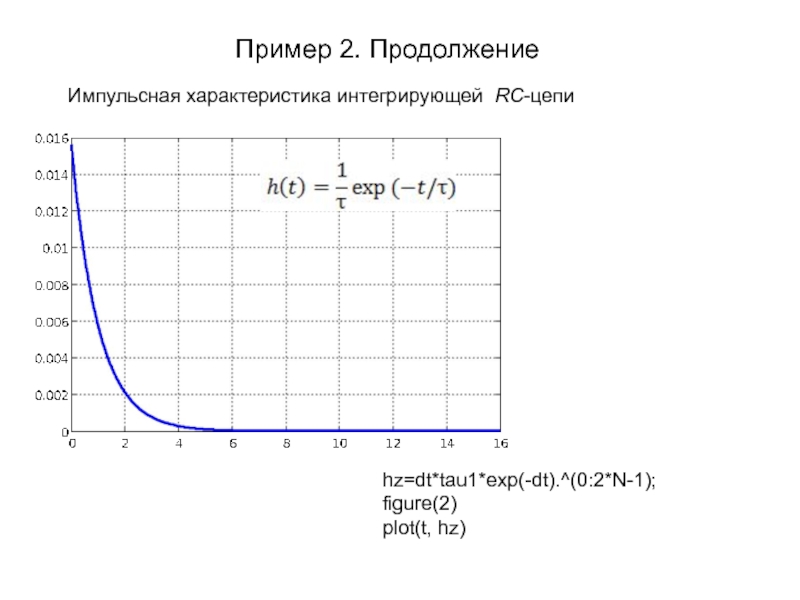
Импульсная характеристика интегрирующей RC-цепи
hz=dt*tau1*exp(-dt).^(0:2*N-1);
figure(2)
plot(t, hz)
Слайд 14Пример 2. Продолжение
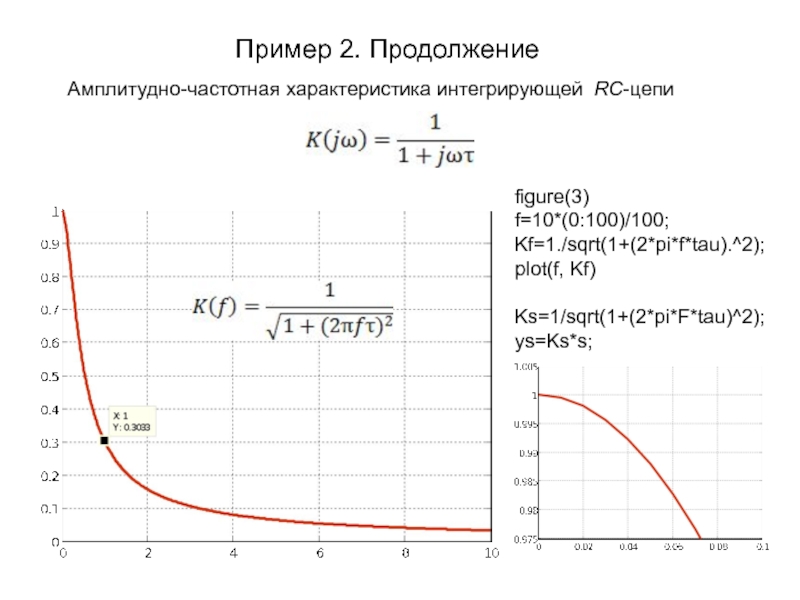
Амплитудно-частотная характеристика интегрирующей RC-цепи
figure(3)
f=10*(0:100)/100;
Kf=1./sqrt(1+(2*pi*f*tau).^2);
plot(f, Kf)
Ks=1/sqrt(1+(2*pi*F*tau)^2);
ys=Ks*s;
Слайд 15Пример 2. Продолжение
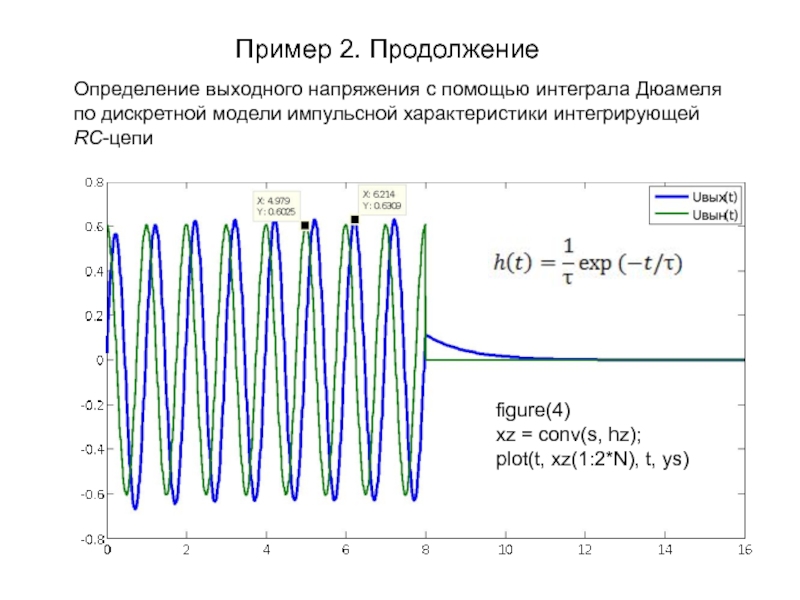
Определение выходного напряжения с помощью интеграла Дюамеля по
дискретной модели импульсной характеристики интегрирующей RC-цепи
figure(4)
xz = conv(s, hz);
plot(t, xz(1:2*N),
t, ys)
Слайд 16Пример 2. Продолжение
Определение выходного напряжения с помощью спектрального метода по
дискретной модели частотной характеристики интегрирующей RC-цепи
[bd, ad]=bilinear(1, [tau 1], Fd);
y1=filter(bd,
ad, s);
figure(5)
plot(t, y1, t, ys)
Слайд 17Условие физической реализуемости
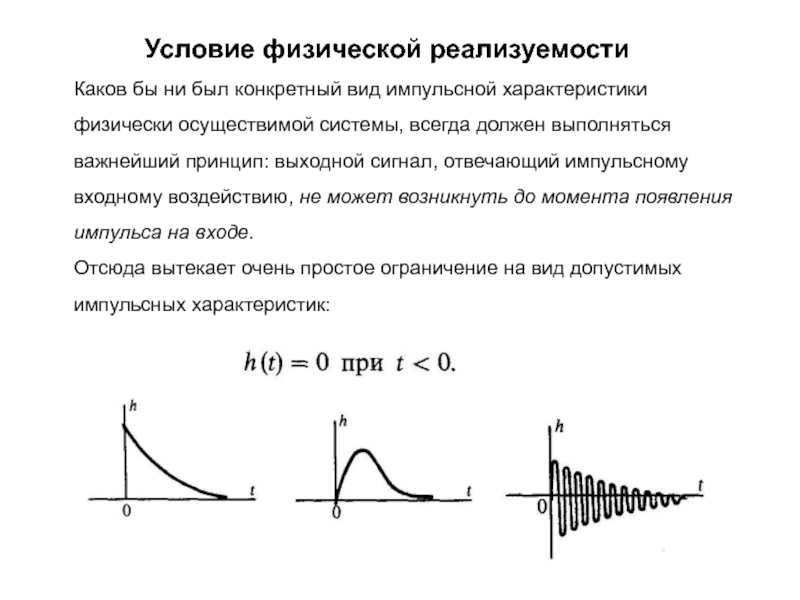
Каков бы ни был конкретный вид импульсной характеристики
физически осуществимой системы, всегда должен выполняться важнейший принцип: выходной сигнал,
отвечающий импульсному входному воздействию, не может возникнуть до момента появления импульса на входе.
Отсюда вытекает очень простое ограничение на вид допустимых импульсных характеристик:
Слайд 18Условие физической реализуемости
Для физически реализуемой системы верхний предел в формуле
интеграла Дюамеля может быть заменен на текущее значение времени:
Третья форма
Эта формула имеет ясный физический смысл: линейная стационарная система, выполняя обработку поступающего на вход сигнала, проводит операцию взвешенного суммирования всех его мгновенных значений, существовавших «в прошлом» при - со < х < t. Роль весовой функции выполняет при этом импульсная характеристика системы.
Физически реализуемая система ни при каких обстоятельствах не способна оперировать «будущими» значениями входного сигнала.
Физически реализуемая система должна быть, кроме того, устойчивой. Это означает, что ее импульсная характеристика должна удовлетворять условию абсолютной интегрируемости
Слайд 19Линейные динамические системы
Линейными динамическими системами принято называть устройства, характеризуемые следующим
свойством: их выходной сигнал определяется не только величиной входного сигнала
в рассматриваемый момент времени, но и «предысторией» этого сигнала. Иначе говоря, динамическая система обладает некоторой конечной или бесконечной «памятью», от характера которой зависят особенности преобразования входного сигнала.
Слайд 20Системы, описываемые дифференциальными уравнениями
Среди всевозможных динамических систем большое значение для
теоретической радиотехники имеют те, которые описываются дифференциальными операторами. В общем
случае речь идет о системах, для которых связь между одномерными входным и выходным сигналами устанавливается с помощью следующего дифференциального уравнения:
Слайд 21Системы, описываемые дифференциальными уравнениями
Предположим, что входной сигнал uBX(t) задан. Тогда
правая часть уравнения, которую можно условно обозначить
, является известной функцией. Анализ поведения системы сводится при этом к хорошо изученной в математике проблеме решения линейного дифференциального уравнения n-го порядка с постоянными коэффициентами:
Порядок n этого уравнения принято называть порядком динамической системы.
Слайд 22Пример 3
Дана RC-цепь вида Г-образного четырехполюсника, возбуждаемая со стороны входа
источником ЭДС um(t). Выходным сигналом служит напряжение на конденсаторе.
Поскольку
ток в цепи то используя второй
закон Кирхгофа, получаем дифференциальное уравнение
RC-цепь служит примером динамической системы 1-го порядка. Важнейший параметр этой цепи — постоянная времени = RC, определяющая характерный временной масштаб протекания процессов в системе.
Слайд 23Пример 4
Дана более сложная система, образованная двумя RC-цепями, которые разделены
идеальным усилителем с коэффициентом усиления Ко. Входное сопротивление усилителя неограниченно
велико, а выходное сопротивление бесконечно мало, поэтому усилитель является идеальным элементом развязки между цепями.
Вводя две постоянные времени и по аналогии с предыдущим примером имеем следующие дифференциальные уравнения 1-го порядка:
Слайд 24Пример 4. Продолжение
Исключив отсюда вспомогательную величину и1, получаем дифференциальное уравнение
цепи:
Рассмотренная здесь более сложная RC-цепь оказывается уже системой 2-го
порядка.
Слайд 25Пример 5
Найти дифференциальное уравнение параллельного колебательного контура с потерями, считая,
что входным сигналом служит ток i(t), а выходным сигналом является
напряжение u(t) на контуре.
Суммируя токи
получаем уравнение
Слайд 26Пример 5. Продолжение
которое путем однократного дифференцирования по времени приводится к
виду
где
— коэффициент затухания контура,
— частота собственных колебаний в контуре без потерь.
Слайд 27Собственные колебания динамических систем
Чтобы полностью определить поведение динамической системы, описываемой
дифференциальным уравнением, требуется учесть начальные условия, которые характеризуют внутреннее состояние
системы в некоторый фиксированный момент времени.
Обычно принято задавать искомую функцию и ее n - 1 производную при
Из теории дифференциальных уравнений известно, что решением дифференциального уравнения, удовлетворяющим любым начальным условиям, является сумма некоторого частного решения неоднородного уравнения, у которого правая часть f(t) отлична от нуля, и общего решения однородного уравнения
Слайд 28Собственные колебания динамических систем
Проблема решения однородного дифференциального уравнения связана с
нахождением корней характеристического уравнения системы
Данное уравнение имеет ровно n корней.
Поскольку коэффициенты уравнения вещественны, корни могут быть либо вещественными, либо комплексно-сопряженными. Если все корни различны, то общее решение однородного уравнения, которое описывает собственные колебания системы, имеет вид
где — постоянные числа, определяемые из начальных условий.
Слайд 29Собственные колебания динамических систем
Если же некоторые из корней оказываются кратными,
то составляющие общего решения однородного уравнения несколько усложняются за счет
появления секулярных (вековых) множителей. Так, если
представляет собой k-кратный корень, то ему отвечает совокупность собственных колебаний вида
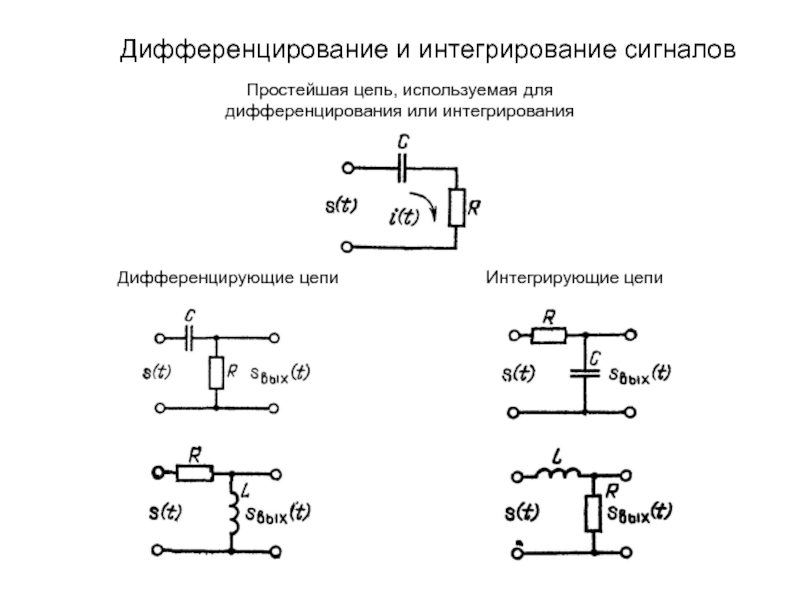
Слайд 30Дифференцирование и интегрирование сигналов
Простейшая цепь, используемая для дифференцирования или интегрирования
Дифференцирующие
цепи
Интегрирующие цепи





![РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 16 Пример 2На вход интегрирующей RC-цепи подаётся радиоимпульсclear allR=1;C=0.5;F=1;N=1024;T=8;dt=T/(N-1);Fd=1/dt;tau=R*C;tau1=1/(R*C);t1=linspace(0,T,N);s=[2*cos(2*pi*F*t1) zeros(1,N)];t=linspace(0,2*T,2*N);figure(1)plot(t,s) Пример 2На вход интегрирующей RC-цепи подаётся радиоимпульсclear allR=1;C=0.5;F=1;N=1024;T=8;dt=T/(N-1);Fd=1/dt;tau=R*C;tau1=1/(R*C);t1=linspace(0,T,N);s=[2*cos(2*pi*F*t1) zeros(1,N)];t=linspace(0,2*T,2*N);figure(1)plot(t,s)](/img/thumbs/9abd8a1c084e6c103de85638c241037c-800x.jpg)
![РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 16 Пример 2. ПродолжениеОпределение выходного напряжения с помощью спектрального метода по дискретной Пример 2. ПродолжениеОпределение выходного напряжения с помощью спектрального метода по дискретной модели частотной характеристики интегрирующей RC-цепи[bd, ad]=bilinear(1,](/img/thumbs/559f87cc23a3954a2770f54e268de9e9-800x.jpg)