Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раскраска графов
Содержание
- 1. Раскраска графов
- 2. Немного историиПервой работой теории графов как математической
- 3. Что такое граф?Графом называется набор точек (эти
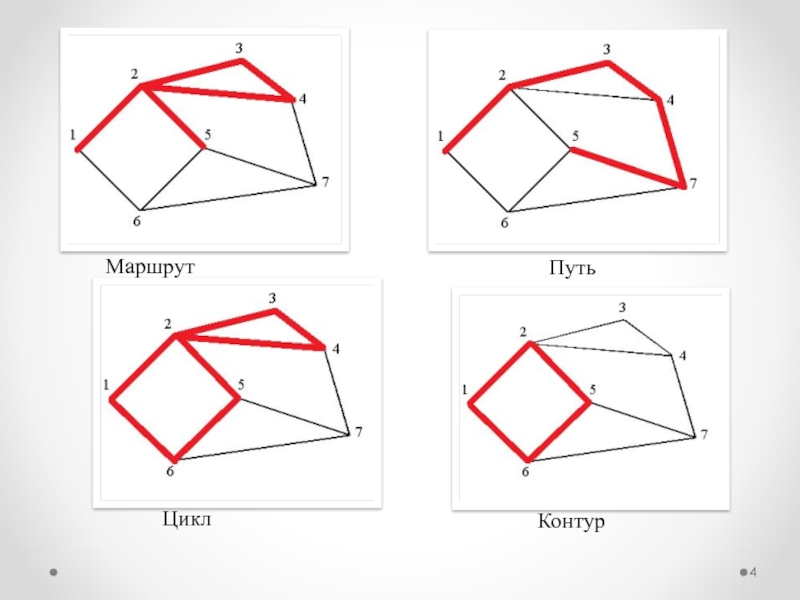
- 4. МаршрутПутьЦиклКонтур
- 5. ОпределениеРаскраской вершин графа называется назначение цветов его вершинам.
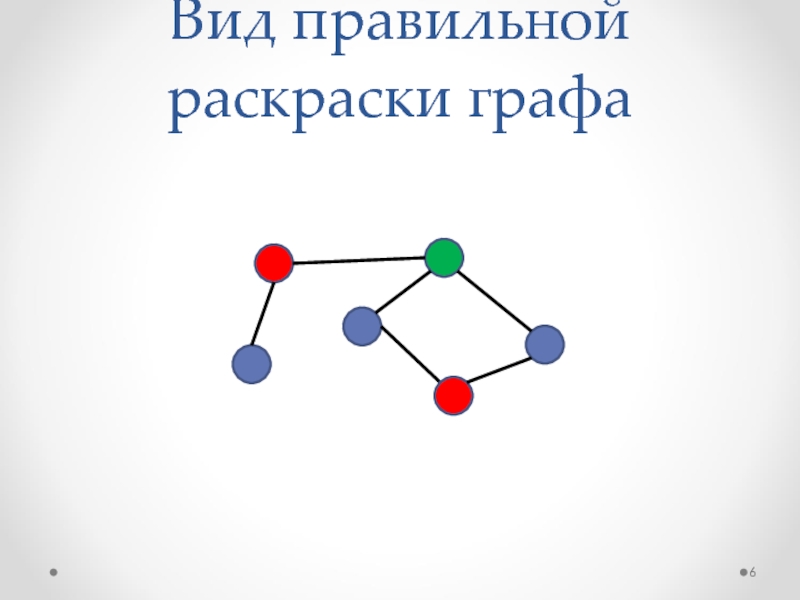
- 6. Вид правильной раскраски графа
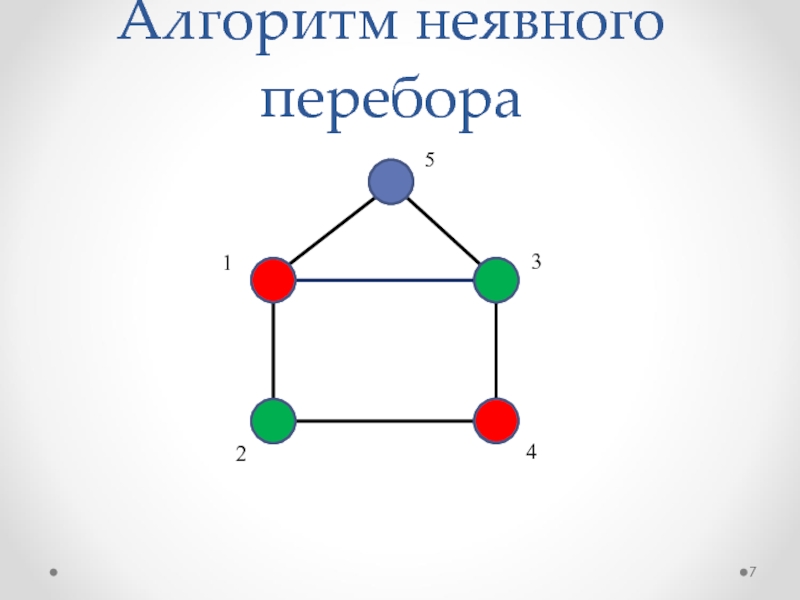
- 7. Алгоритм неявного перебора12435
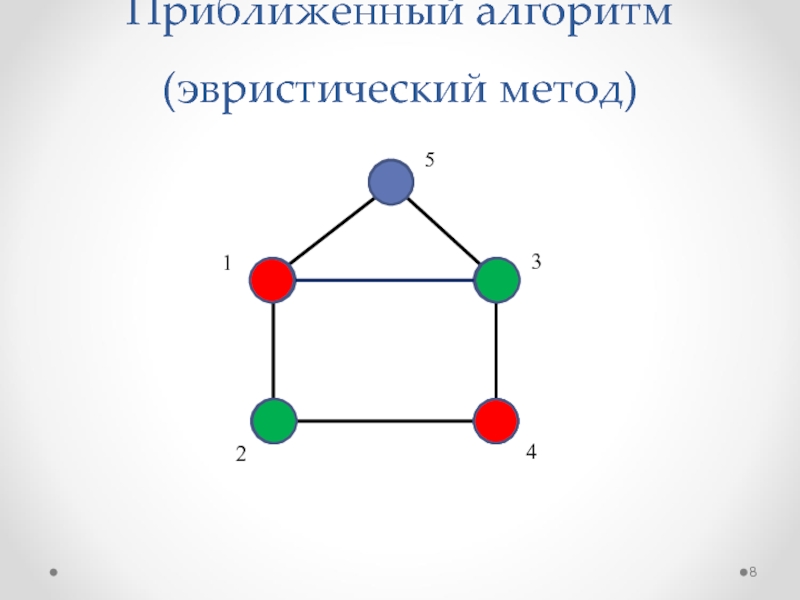
- 8. Приближенный алгоритм (эвристический метод)12435
- 9. Раскраска ребер графаМинимальное число цветов, необходимое для
- 10. Применения задач о раскраскеТеория расписаний.Распределение ресурсов.При конструировании различных устройств.
- 11. Спасибо за внимание!
- 12. Скачать презентанцию
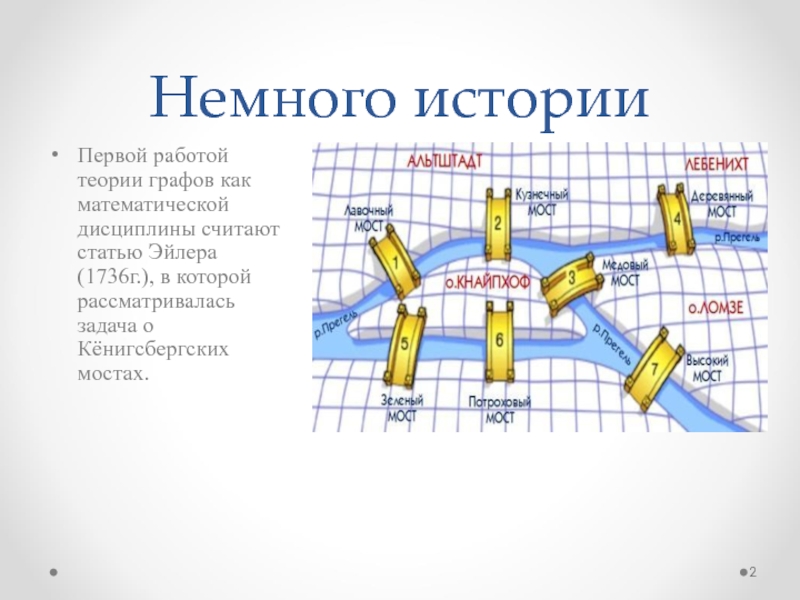
Немного историиПервой работой теории графов как математической дисциплины считают статью Эйлера (1736г.), в которой рассматривалась задача о Кёнигсбергских мостах.
Слайды и текст этой презентации
Слайд 2Немного истории
Первой работой теории графов как математической дисциплины считают статью
Эйлера (1736г.), в которой рассматривалась задача о Кёнигсбергских мостах.
Слайд 3Что такое граф?
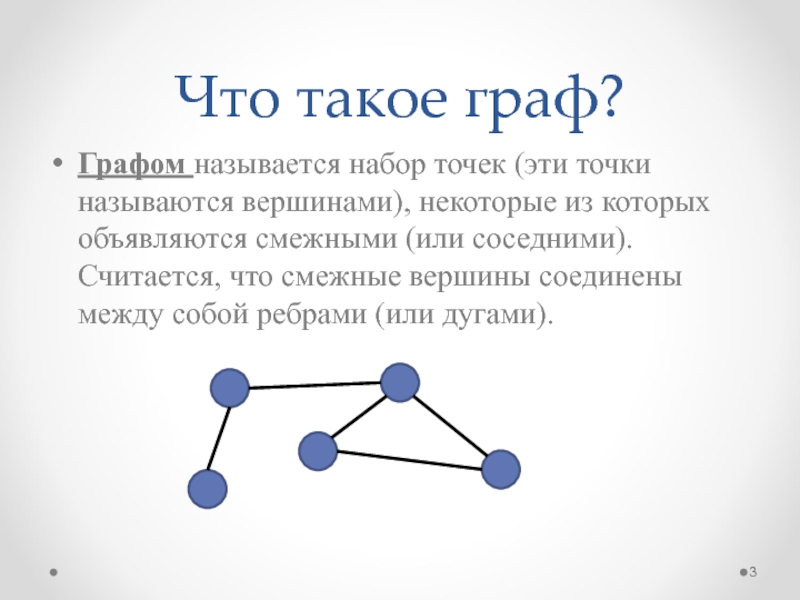
Графом называется набор точек (эти точки называются вершинами),
некоторые из которых объявляются смежными (или соседними). Считается, что смежные
вершины соединены между собой ребрами (или дугами).
Слайд 5Определение
Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета -
это числа 1,2…k . Тогда раскраска является функцией, определенной на множестве
вершин графа и принимающей значения в множестве {1,2…k}. Раскраску можно также рассматривать как разбиение множества вершин V = V1 u V2 u…u Vk, где Vi - множество вершин цвета i .Наименьшее число цветов, необходимых для раскраски графа, называется хроматическим числом графа и обозначается χ(G).
Слайд 9Раскраска ребер графа
Минимальное число цветов, необходимое для правильной раскраски ребер
графа G, называется хроматическим индексом графа и обозначается через χ’(G) .
Теорема Визинга. Если в
графе максимальная степень вершин равна δ, то реберно-хроматическое число равно либо δ, либо δ +1.
Слайд 10Применения задач о раскраске
Теория расписаний.
Распределение ресурсов.
При конструировании различных устройств.
