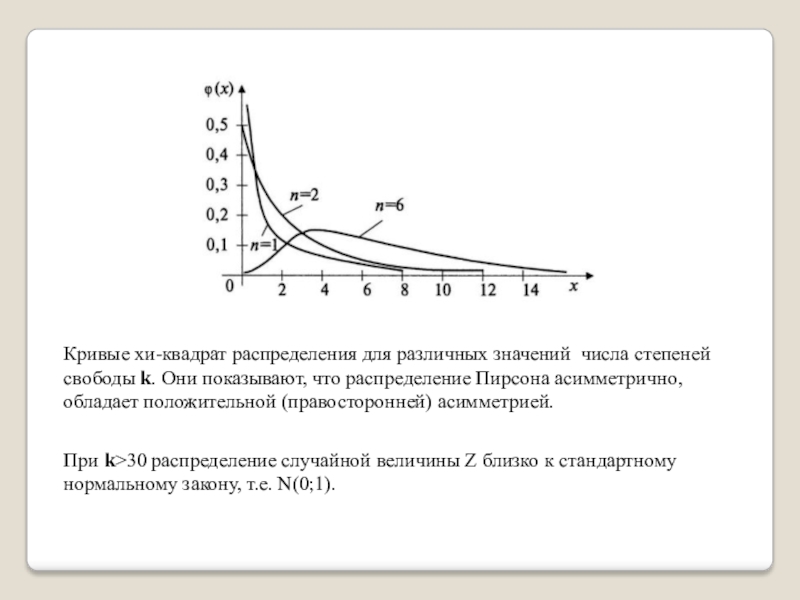
Распределения Стьюдента и Пирсона

распределение суммы квадратов k независимых случайных величин, распреде-
лённых по стандартному

Его плотность вероятности имеет вид:

где Zi (i=1,2,…,k) имеет нормальное распределение N(0;1).

Для целых положительных
значений:

Они показывают, что распределение Пирсона асимметрично,
обладает положительной (правосторонней) асимметрией.
При k>30

– случайная величина, распределённая по стандартному нормальному
закону, т.е. N(0;1).
независимая

Плотность вероятности распределения Стьюдента имеет вид:

кривая, кривая t-распределения симметрична относительно оси
ординат, но по сравнению

При устремлении k к бесконечности t-распределение приближается к нормальному.
Практически уже при k>30 можно считать t-распределение приближённо
нормальным.

Математическое ожидание случайной величины, имеющей t-распределение , в силу
симметрии её кривой распределения равно нулю, а дисперсия равна k/(k-2).

имеет нормальное распределение).
Формула доверительной вероятности для малой выборки:
- предельная ошибка

Доверительный интервал для генеральной средней:

отклонение числа зарегистрированных частиц среди
отобранных приборов составило 30. Найти вероятность

дисперсии:
Для среднеквадратичного отклонения:

числа распадов этих образцов составило 15.
Предполагая, что количество распадов