Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распределительный метод
Содержание
- 1. Распределительный метод
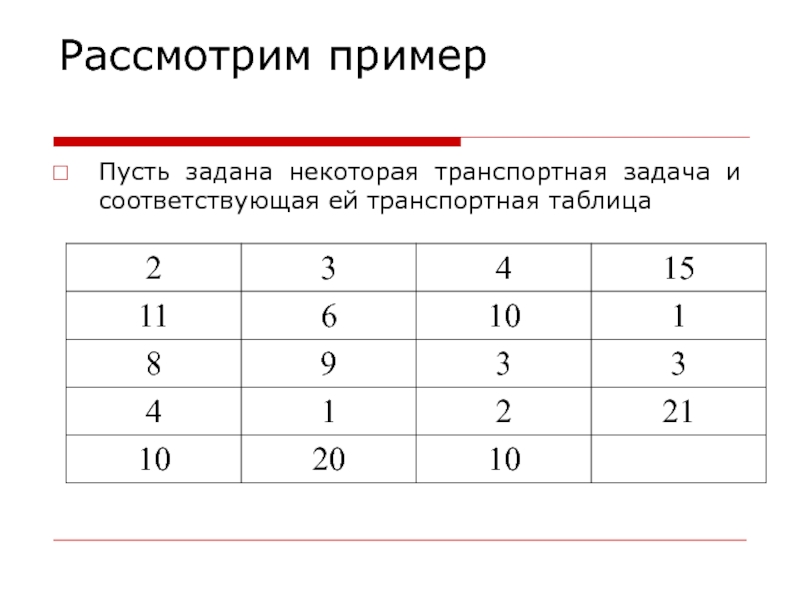
- 2. Рассмотрим примерПусть задана некоторая транспортная задача и соответствующая ей транспортная таблица
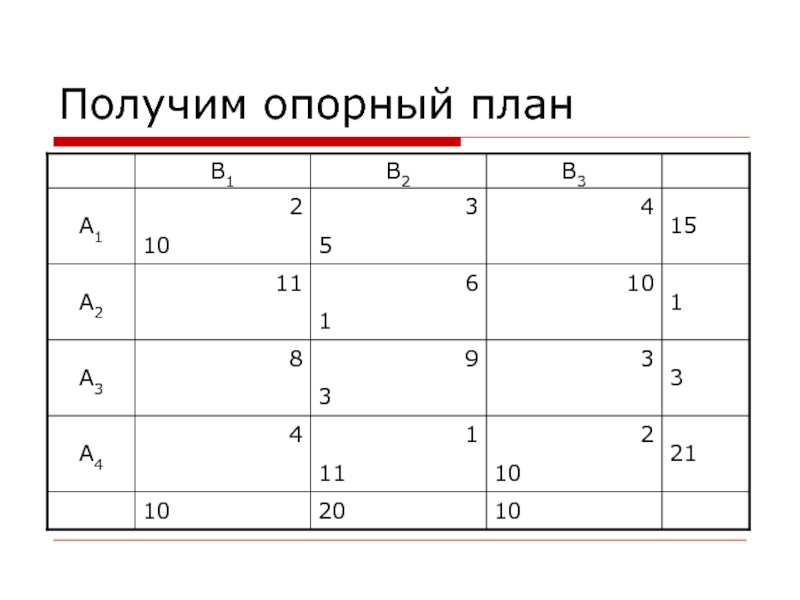
- 3. Получим опорный план
- 4. Улучшение плана перевозокСтоимость этого плана равна:L =
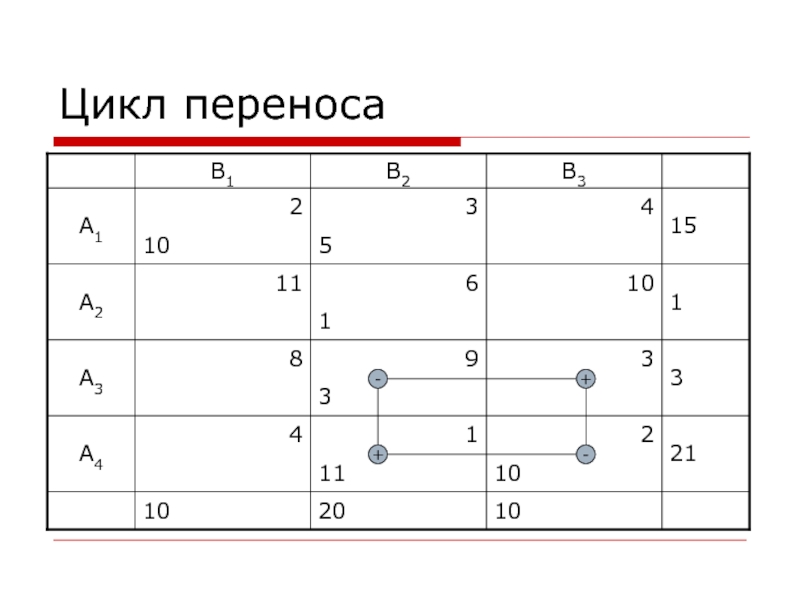
- 5. Цикл переноса--++
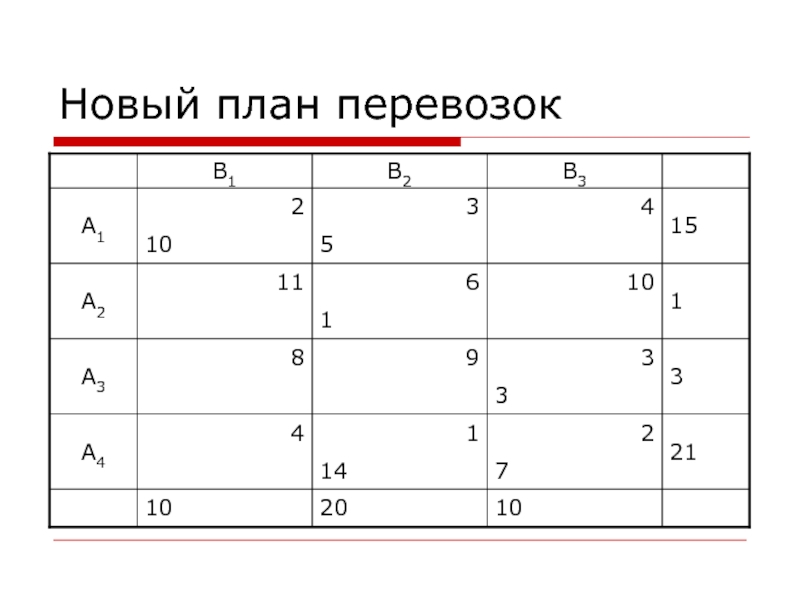
- 6. Новый план перевозок
- 7. Цикл пересчетаСтоимость этого плана равна:L = 10×2
- 8. Цикл пересчета. ОпределениеИтак, циклом в транспортной таблице
- 9. Распределеительный метод решения транспортной задачиДанный метод состоит
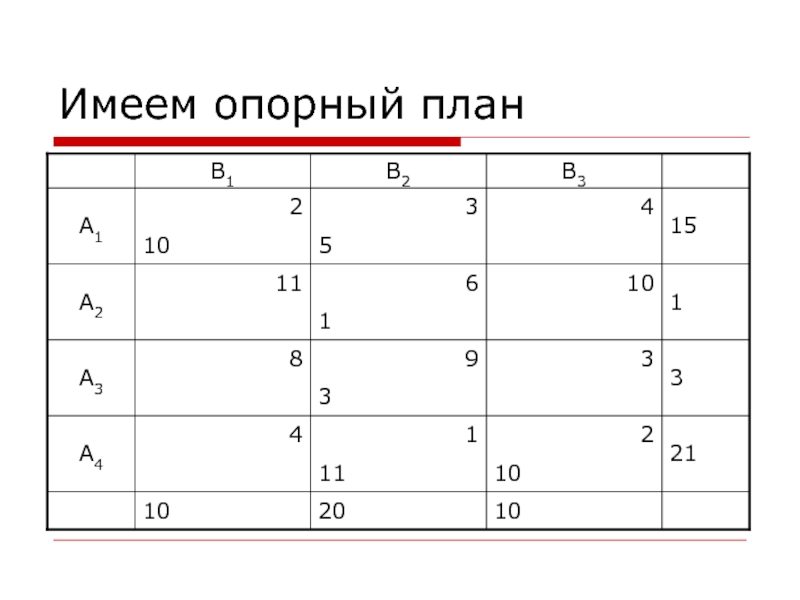
- 10. Имеем опорный план
- 11. Улучшим полученный планВычислим цену цикла для каждой
- 12. Пересчет перевозокДля всех свободных переменных (клеток) с
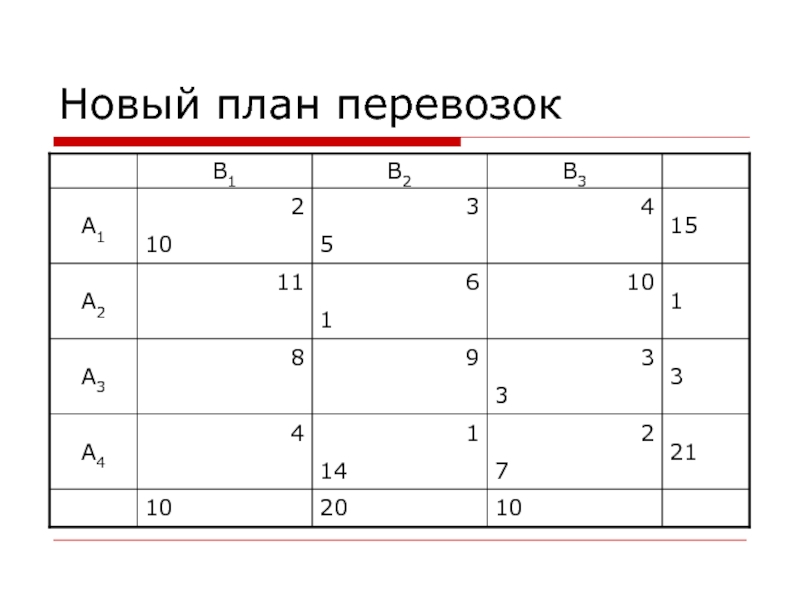
- 13. Новый план перевозок
- 14. Улучшим полученный планВычислим цену цикла для каждой
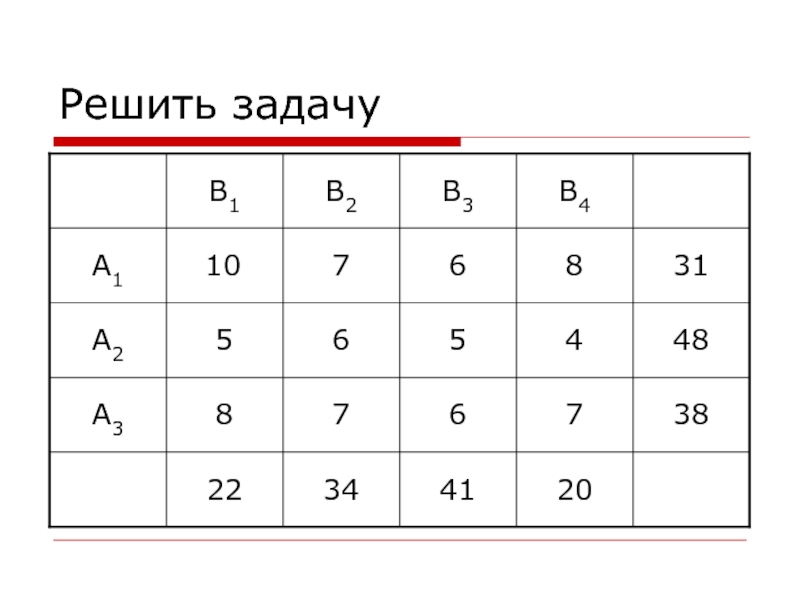
- 15. Решить задачу
- 16. Скачать презентанцию
Рассмотрим примерПусть задана некоторая транспортная задача и соответствующая ей транспортная таблица
Слайды и текст этой презентации
Слайд 2Рассмотрим пример
Пусть задана некоторая транспортная задача и соответствующая ей транспортная
таблица
Слайд 4Улучшение плана перевозок
Стоимость этого плана равна:
L = 10×2 + 5×3
+ 1×6 + 3×9 + 11×1 + 10×2 = 99.
Попробуем
улучшить полученный план, перенеся, как показано в приведенной выше таблице, 3 единицы из клетки (3,2) в клетку (3,3) и, чтобы не нарушать баланса, перенесем те же 3 единицы из клетки (4,3) в клетку (4,2). В результате переноса мы получили новый план перевозок, который тоже будет допустимым, так как переброску груза с одного маршрута на другой мы осуществляли циклически, заботясь о сохранении баланса заявок и запасов.Слайд 7Цикл пересчета
Стоимость этого плана равна:
L = 10×2 + 5×3 +
1×6 + 3×3 + 14×1 + 7×2 = 78.
Очевидно, что
полученный план перевозок по стоимости предпочтительнее первоначального опорного плана.Из приведенной таблицы видно, что за счет циклической перестановки грузоперевозок объемом 3 единицы по маршрутам (3,2)-, (3,3)+, (4,3)-, (4,2)+ удалось понизить стоимость плана перевозок на 126 условных единиц стоимости.
Здесь следует обратить внимание на следующее равенство:
78 – 99 = - 21 = 3×( - 9 + 3 - 2 + 1) = 3 × (-7).
Рассмотрев на практическом примере принципы, лежащие в основе методов улучшения планов перевозок, формально определим некоторые из использованных нами при этом понятий.
Слайд 8Цикл пересчета. Определение
Итак, циклом в транспортной таблице назовем несколько клеток,
соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот
на угол, равный 90о. Условимся помечать символами (+) те вершины ломаной линии, образующей цикл, в которых объемы перевозок увеличивается, а символом (-) те вершины цикла, в которых они уменьшаются.Очевидно, что прямоугольник представляет собой наиболее простой случай такой замкнутой ломаной линии.
Цикл с отмеченными вершинами будем называть «означенным». Перенести какое-то количество единиц груза по означенному
циклу – это означает увеличить объемы перевозок в положительных вершинах (вершинах, помеченных символом «+») на это количество единиц и одновременно с этим уменьшить перевозки на то же количество в отрицательных вершинах (вершинах, помеченных символом «–»).
Очевидно что, при переносе любого числа единиц по циклу равновесие между запасами и заявками не меняется.
Назовем ценой (стоимостью) цикла (g) – алгебраическую сумму стоимостей, стоящих в вершинах цикла, с учетом знака этих вершин, например:
g1 = с21 – с23 + с43 – с41,
g2 = с34 – с35 + с55 – с54 + с14 – с16.
Слайд 9Распределеительный метод решения транспортной задачи
Данный метод состоит в последовательном улучшении
опорного плана перевозок путем отыскания на каждом шаге выгодных циклов
переноса грузов.Более подробно рассмотрим теперь процесс формирования очередного цикла переноса на каждом новом шаге алгоритма.
Очевидно, что при перемещении х единиц груза по некоторому циклу с ценой g стоимость перевозок изменяется на величину X × g.
Тогда, для улучшения текущего плана перевозок имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна.
Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что оптимальный план достигнут.
При улучшении плана циклическими переносами пользуются приемом, заимствованным из симплекс-метода: на каждом шаге (цикле) заменяют одну свободную переменную на базисную, т.е. заполняют одну клетку и взамен того освобождают одну из базисных клеток.
Можно доказать, что для любой свободной клетки транспортной таблицы всегда существует цикл (и притом единственный), одна из вершин которого лежит в этой клетке, а все остальные в базисных клетках. Если цена такого цикла, с плюсом в свободной клетке, отрицательна, то план можно улучшить. Количество единиц груза (х), которые можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла.
Слайд 11Улучшим полученный план
Вычислим цену цикла для каждой свободной клетки. Количество
свободных клеток в транспортной таблице данного опорного плана равно: k
= 6.γ13 = 4 – 3 + 1 – 2 = 0
γ21 = 11 – 2 + 3 – 6 = 6
γ23 = 10 – 6 + 1 – 2 = 3
γ31 = 8 – 2 + 3 – 9 = 0
γ33 = 3 – 9 + 1 – 2 = – 7
γ41 = 4 – 2 + 3 – 1 = 4
Слайд 12Пересчет перевозок
Для всех свободных переменных (клеток) с отрицательной ценой цикла
вычислим максимальное количество груза, которое можно перенести по соответствующему циклу.
Очевидно, что максимальное количество груза, которое можно переместить по некоторому выбранному циклу будет равно минимальному значению груза среди отрицательных клеток цикла.max x33 = min ( 3, 10) = 3.
Теперь для всех свободных переменных с отрицательной ценой циклов вычислим характеристику γ33×max x33. Полученные значения будем использовать при выборе конкретного цикла пересчета на данной итерации алгоритма.
Выберем ту свободную переменную, которой соответствует наименьшее значение величины γij×max xij и перенесем единиц груза по циклу, соответствующему выбранной переменной:
(ij) = (3,3); g33=-7; max x33=3; γ33×max x33=-21.
Таким образом, мы уменьшим значение целевой функции L – стоимость плана перевозок – на 21 единицу. Новому улучшенному плану перевозок будет соответствовать следующая таблица перевозок
Слайд 14Улучшим полученный план
Вычислим цену цикла для каждой свободной клетки. Количество
свободных клеток в транспортной таблице данного опорного плана равно: k
= 6.γ13 = 4 – 3 + 1 – 2 = 0
γ21 = 11 – 2 + 3 – 6 = 6
γ23 = 10 – 6 + 1 – 2 = 3
γ31 = 8 – 3 + 2 – 1 + 3 – 2 = 7
γ32 = 9 – 1 + 2 – 3 = 7
γ41 = 4 – 2 + 3 – 1 = 4
Так как не существует циклов свободных переменных с отрицательной ценой, полученный план перевозок является оптимальным. Стоимость оптимального плана перевозок составляет 78 единиц.