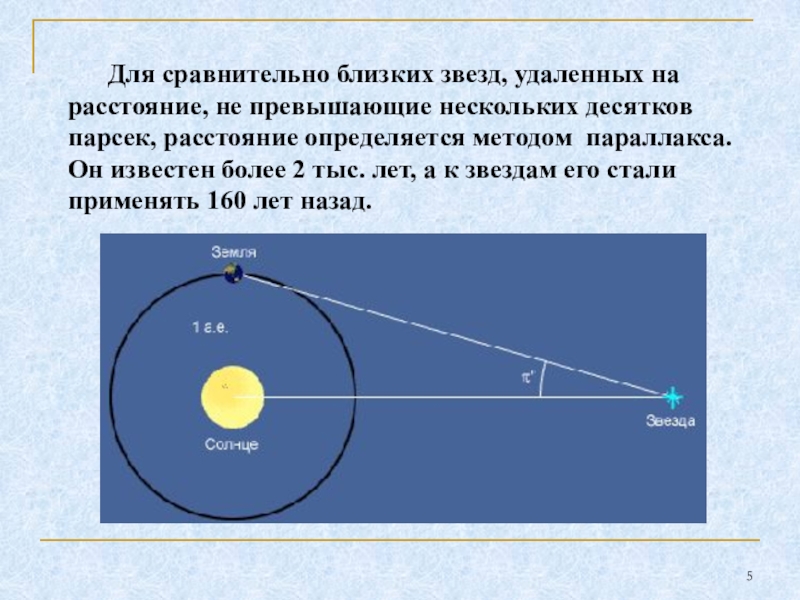
Меркурия и Венеры в моменты элонгации (из прямоугольного треугольника по
углу элонгации).1-й способ: (приближенный) По третьему закону Кеплера можно определить удаленность планеты от Солнца, зная периоды обращений и одно из расстояний.
Элонгация — одна из конфигураций планет: положение планеты, при котором её угловое расстояние от Солнца максимально