Растровые алгоритмы и характеристики растра

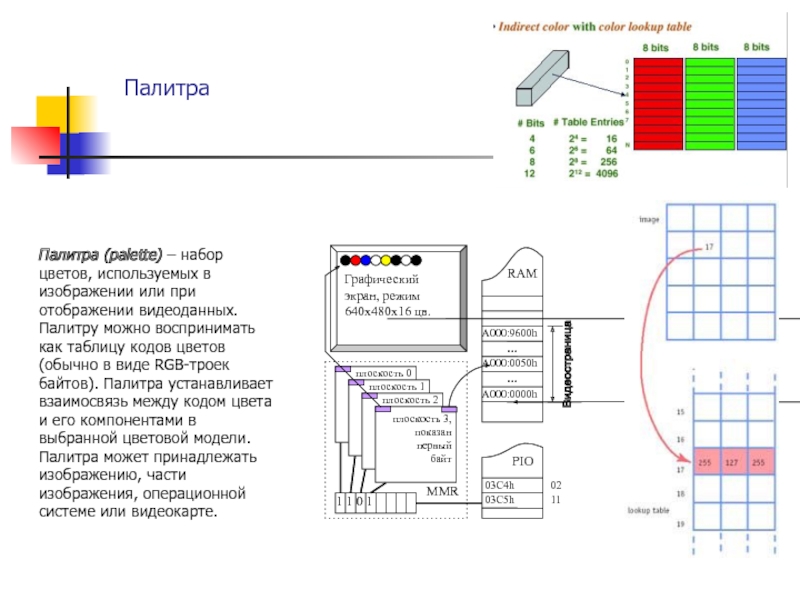
изображения или устройства графического вывода. Согласно психофизиологическим исследованиям глаз человека

способен различать 350 000 цветов.
Однако в компьютерной графике в настоящее время используются изображения с формально гораздо большей глубиной цвета (16.7 млн цветов), тем не менее следует учитывать, что для синтезированных цветов на каждый из компонентов цвета в этом случае отводится только 256 градаций, которые достаточно хорошо различимы глазом человека.

Классифицируем изображения следующим образом:
бинарные – 1 бит на пиксель – обычно чёрно-белые изображения
полутоновые – 1 байт на пиксель – изображение в градациях серого
Hi Color – 16 бит на пиксель – 65536 цветов
True Color – от 24 бит на пиксель (16,7 млн. цветов) до 48 бит на пиксель

128

отображении видеоданных. Палитру можно воспринимать как таблицу кодов цветов (обычно

в виде RGB-троек байтов). Палитра устанавливает взаимосвязь между кодом цвета и его компонентами в выбранной цветовой модели. Палитра может принадлежать изображению, части изображения, операционной системе или видеокарте.

изображения и измеряется обычно в dpi (dots per inch)
dpi

= 25.4 / dP

Связность – соседство двух пикселей в растровом изображении

из вариантов антиалисинга:
пиксель делится на 4 равные части.

n x n можно получить n 2+1 различных градаций
При

регулярном расположении одинаковых ячеек образуются паразитные текстуры, муар. Поэтому наряду с ячейками с фиксированным рисунком используются методы частотно-модулированного дизеринга (равномерное псевдослучайное распределение пикселей по ячейке) и диффузного дизеринга (распределение в каждой ячейке создаётся случайным образом).

{
y=y1+((x-x1)*(y2-y1))/(x2-x1);
SetPixel(x,y);
}
float k = (float) (y2-y1) / (float) (x2-x1);
for

(x=x1; x<=x2; x++)
{
y=y1+ (float) (x-x1) * k;
SetPixel(x,y);
}

float k = (float) (y2-y1) / (float) (x2-x1);
float yy=(float) y1 – (float) x1*k
for (x=x1; x<=x2; x++)
{
y=yy+(float) x*k;
SetPixel(x,y);
}

float k = (float) (y2-y1) / (float) (x2-x1);
float yy = y1;
for (x=x1; x<=x2; x++)
{
yy += k; y = yy
SetPixel(x,y);
}

x·Δy/Δx
Рi-1= (xi-1,yi-1)
Si = (xi, yi-1)

x2 - x1; int dy = y2 - y1; int d =

2 * dy - dx;
int d1 = 2*dy;
int d2 = 2*(dy - dx);
SetPixel(x1, y1, color);
for (int x = x1 + 1; int y = y1; x <= x2; x++)
{ if (d < 0) { d += d1;
} else {
d += d2;
y += 1; }
SetPixel( x, y, color); }

x1, int y1, int x2, int y2, int color)
{
int dx

= x2 - x1;
int dy = y2 - y1;
int d = 0;
int d1 = dy << 1;
Int d2 = - ( dx << 1 );
SetPixel (x1, y1, color);
for ( int x = x1, y = y1, i = 1; i <= dx + dy; i++ ) {
if ( d > 0 ) {
d += d2; y += 1;
} else {
d += d1; x += 1;
}
SetPixel ( x, y, color);
}
}

a2b2
x
a
b



y2 = r2 – x2
Sin()
y
void Circle(int Xc,int Yc,int

radius,int c)
{
int x,y,d;
d = 3 - ( radius << 1);
x = 0; y = radius;
While ( x < y ) {
Set8Pixels( Xc, Yc, x, y, c );
If ( d > 0 ) {
d = d + ( x << 2 ) + 6;
} else {
d = d + ( (x-y) << 2 ) + 10;
y--;
}
x++;
}
}

Область может содержать полости и быть сколь угодно сложной формы.

Необходимо лишь, чтобы внешняя граница и границы полостей были 8-связны и их цвет отличался от цвета заполнения.

void PixelFill (int x, int y, int BC, int color)
{
int c = GetPixel ( x, y );
If (( c != BC ) && ( c != color ))
{
SetPixel ( x, y, color );
PixelFill ( x – 1, y, BC, color );
PixelFill ( x + 1, y, BC, color );
PixelFill ( x, y – 1, BC, color );
PixelFill ( x, y + 1, BC, color );
}
}

(xst, yst) и начальное направление действия рекурсивных вызовов dir=1. Параметры

левой и правой границы вначале совпадают с координатой затравочной точки: xPL = xst, xPR = xst. Вызывается процедура LineFill, в которой:
Находятся xL и xR – левая и правая границы, между которыми проводится текущая горизонтальная линия.
Делается приращение у=у+dir и, между xL и xR, анализируется цвет пикселей над линией. Если он не совпадает с цветом заполнения, процедура LineFill вызывается рекурсивно с dir = 1 и xPL = xL, xPR = xR.
Делается приращение y=y–dir и, начиная от xL до предыдущего значения xPL анализируется цвет пикселей под линией. Если цвет пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.
Продолжая по той же горизонтали от предыдущего xPR до xR анализируется цвет под линией. Если цвет какого-либо пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.

XPL

XPR

XL

XR