КОНИЧЕСКИЕ СЕЧЕНИЯ

образованную прямыми, проходящими через вершину конуса и точки окружности основания

Сечения конической поверхности плоскостью можно рассматривать как центральную проекцию окружности основания конуса на эту плоскость. Поэтому, если плоскость параллельна плоскости основания и не проходит через вершину конуса, то в сечении конической поверхности получается окружность.

угол между образующей и этой осью, то в сечении конической

некоторых точках F1, F2 и конической поверхности по окружностям C1

Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF1 = AA1, AF2 = AA2. Поэтому AF1 + AF2 = AA1 + AA2 = A1A2. Но длина отрезка А1А2 не зависит от выбора точки А сечения. Она равна образующей соответствующего усеченного конуса. Поэтому сумма расстояний от точки А до точек F1, F2 будет постоянной.

Пусть А – произвольная точка сечения. Проведем образующую AS и обозначим через А1, А2 точки ее пересечения с окружностями C1, C2 соответственно. Заметим, что прямая AS является касательной к обеим сферам.

диаметры AB и CD.
На образующих SA и SB выберем какие-нибудь

Проведем хорду C1D1, параллельную CD, и точку O1 ее пересечения с AB соединим с S. Точку пересечения SO1 и A’B’ обозначим O1. Через точку O1 проведем прямую, параллельную C1D1 и ее точки пересечения с SC1 и SD1 обозначим C’1 и D’1, соответственно. Они будут принадлежать искомому сечению.

Аналогичным образом построим несколько других точек.

Соединяя их плавной кривой, получим искомое сечение.

между образующей и этой осью, то в сечении конической поверхности

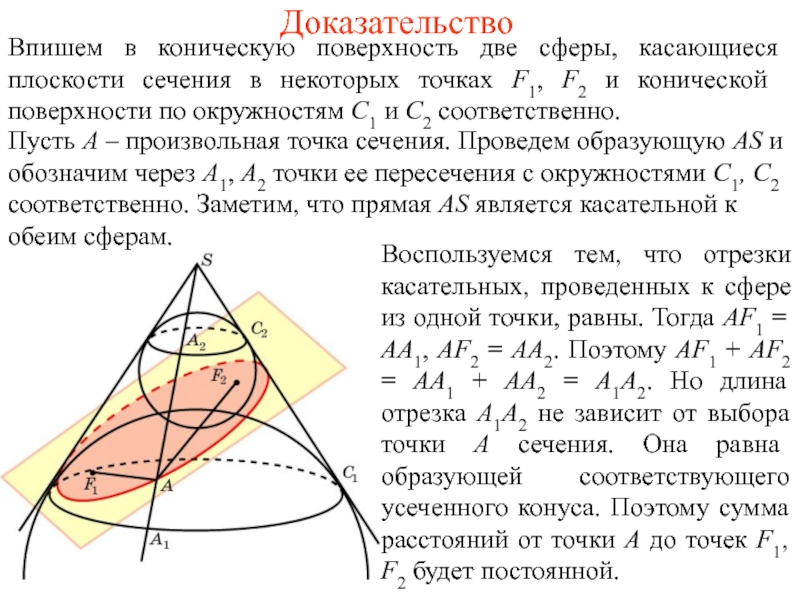
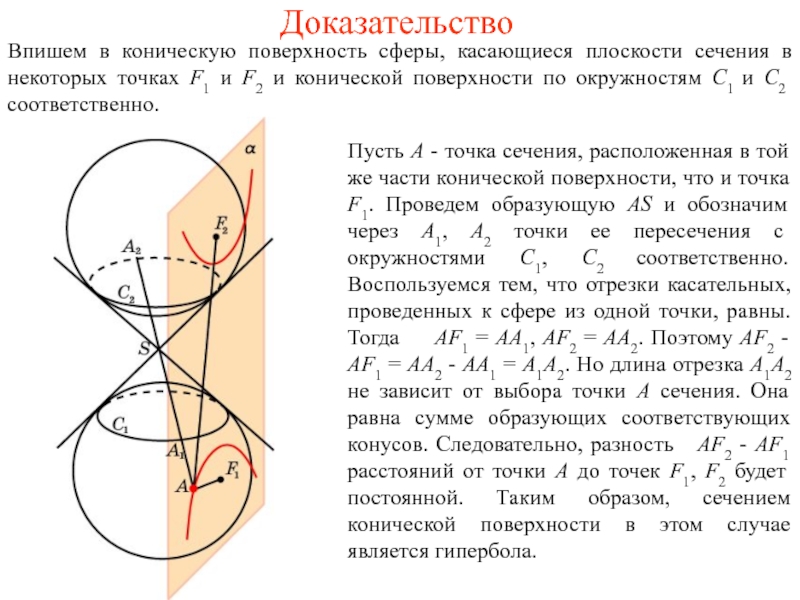
точке F и конической поверхности по окружности C, лежащей в

Пусть А - произвольная точка сечения. Проведем образующую AS и обозначим через А1 точку ее пересечения с окружностью C. Заметим, что прямая AS является касательной к сфере. Прямая AF также является касательной. Отрезки АF и АА1 равны как отрезки касательных, проведенных к сфере из одной точки. Опустим из точки А перпендикуляр АВ на плоскость β и перпендикуляр АD на прямую d.

Угол А1АВ равен φ. Угол АDВ является углом между плоскостями α и β и поэтому равен 90о-φ. Следовательно, угол BAD равен φ. Прямоугольные треугольники АВА1 и АВD равны, так как имеют общий катет и соответственно равные углы. Поэтому АА1 = АD. Окончательно получаем равенство AF = AD, которое означает, что расстояние от произвольной точки сечения до точки F равно расстоянию от этой точки до прямой d, т. е. сечением конической поверхности в этом случае является парабола.

диаметры AB и CD.
Через точку O проведем прямую, параллельную SA

Через какую-нибудь точку O1 диаметра CD проведем прямую AO1 и ее точку пересечения с эллипсом основания обозначим B1. Через точку O1 проведем прямую, параллельную SA и ее точку пересечения с SB1 обозначим B’1. Она будет принадлежать искомому сечению.

Аналогичным образом построим несколько других точек.

Соединяя их плавной кривой, получим искомое сечение.

между образующей и этой осью, то в сечении конической поверхности

точках F1 и F2 и конической поверхности по окружностям C1

Пусть А - точка сечения, расположенная в той же части конической поверхности, что и точка F1. Проведем образующую AS и обозначим через А1, А2 точки ее пересечения с окружностями C1, C2 соответственно. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF1 = AA1, AF2 = AA2. Поэтому AF2 - AF1 = AA2 - AA1 = A1A2. Но длина отрезка А1А2 не зависит от выбора точки А сечения. Она равна сумме образующих соответствующих конусов. Следовательно, разность AF2 - AF1 расстояний от точки А до точек F1, F2 будет постоянной. Таким образом, сечением конической поверхности в этом случае является гипербола.

хорду C1D1, параллельную CD. Через точку O1 ее пересечения с

Аналогичным образом построим несколько других точек.

Соединяя их плавной кривой, получим искомое сечение.

В эллипсе, изображающем основание конуса, проведем сопряженные диаметры AB и CD.

Через какую-нибудь точку O2 хорды C1D1 проведем прямую OO2 и ее точку пересечения с эллипсом обозначим B2. Через точку O2 проведем прямую, параллельную SO и ее точку пересечения с SB2 обозначим B’2. Она будет принадлежать искомому сечению.