Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Основные понятия и аксиомы стереометрии
Содержание
- 1. "Основные понятия и аксиомы стереометрии
- 2. ГеометрияПланиметрияСтереометрия
- 3. Стереометрия изучает свойства фигур в пространстве. Слово «стереометрия»
- 4. Основные понятия в стереометрии:
- 5. Для коротких записей утверждений используют символы :принадлежитне принадлежитподмножествопересечениеобъединениесуществует только единственноесуществуетлюбое, всякое
- 6. Для коротких записей утверждений используют символы :параллельныне параллельныперпендикулярныскрещивающиесяравносильныследует
- 7. Прочитайте чертежAС
- 8. Прочитайте чертежBcba
- 9. Ответьте на вопросы по рисунку:1. Назовите точки,
- 10. Наряду с основными фигурами мы будем рассматривать
- 11. А также тела вращения: шар, сфера, цилиндр, конус.
- 12. В аксиомах стереометрии выражены основные свойства неопределяемых
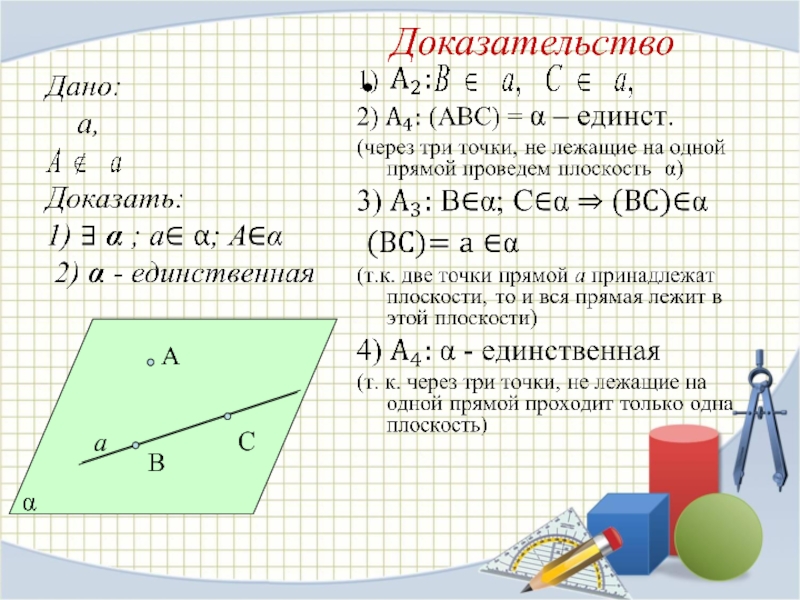
- 13. Аксиома 1Существует хотя бы одна прямая и
- 14. Аксиома 2Через любые две различные точки проходит
- 15. Аксиома 3 Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости АВα
- 16. Аксиома 4 Через три точки, не принадлежащие
- 17. Аксиом 5 Если две различные плоскости имеют
- 18. Аксиома 6 Для любых двух точек А
- 19. Аксиома 7Расстояние от точки А до точки
- 20. Аксиома 8АВС
- 21. Аксиома 9Для каждой плоскости выполняются известные из
- 22. Следствие 1Через прямую и
- 23. Доказательство
- 24. Через две пересекающиеся прямые можно провести одну и только одну плоскость.МabNСледствие 2Т
- 25. Доказательство
- 26. Определение:Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки.
- 27. Следствие 3 Через две различные параллельные прямые можно провести только одну плоскость.
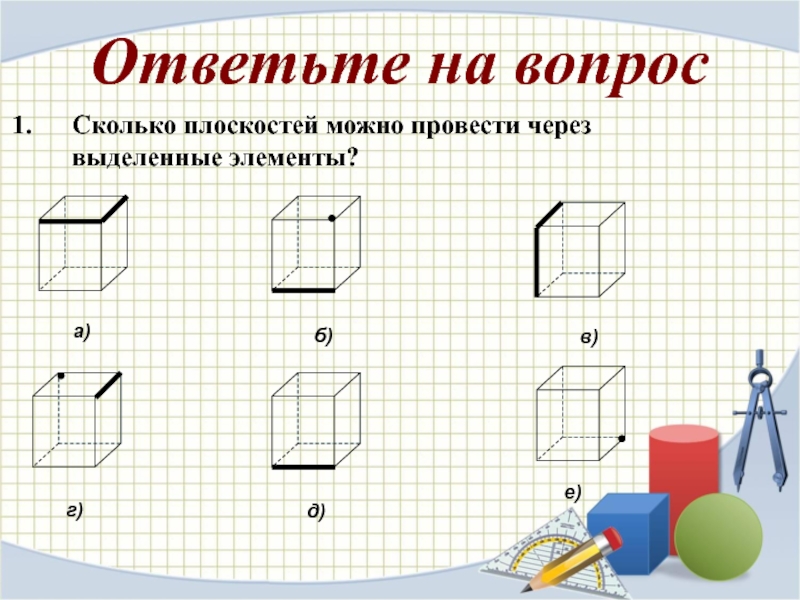
- 28. Сколько плоскостей можно провести через выделенные элементы?а)б)в)г)д)е)Ответьте на вопрос
- 29. Изобразите в тетради куб (видимые линии –
- 30. Дано: куб АВСДА1В1С1Д1Найдите:Несколько точек, которые лежат в
- 31. АВСДА1В1С1Д1αПрямые АА1, АВ, АД проходят через точку
- 32. Назовите плоскости, в которых лежат прямыеРЕ, МК,
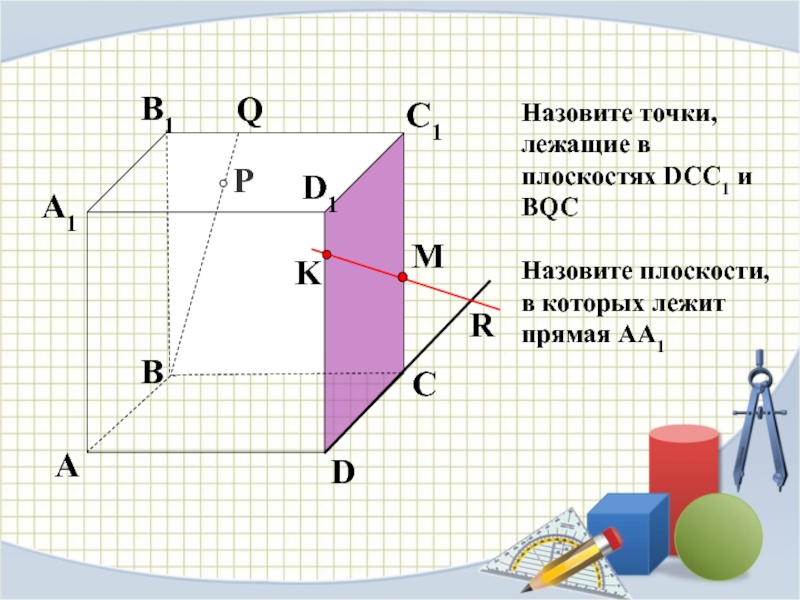
- 33. PABCDA1B1C1D1RMKQНазовите точки, лежащие в плоскостях DCC1 и BQCНазовите плоскости, в которых лежит прямая АА1
- 34. Задания для самостоятельной работы:Задание 1. Запишите с
- 35. Задания для самостоятельной работы:Задание 2. Дан куб
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3 Стереометрия изучает свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих
слов «стереос» объемный, пространственный, «метрео» – мерить.
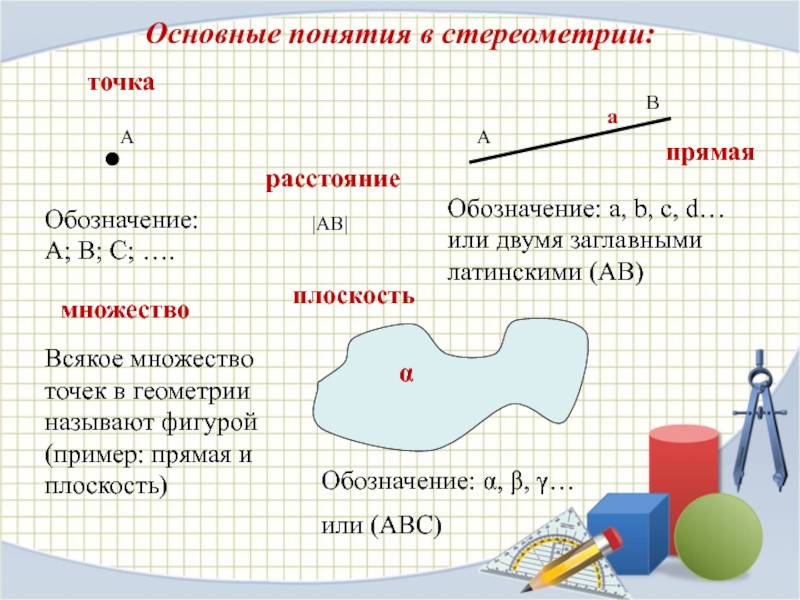
Слайд 4Основные понятия в стереометрии:
точка
Обозначение: А; В; С; ….
Обозначение: a, b, с, d… или двумя заглавными латинскими (АВ)
Обозначение: α, β, γ…
или (АВС)
плоскость
множество
расстояние
Всякое множество точек в геометрии называют фигурой
(пример: прямая и плоскость)
А
В
прямая
|АВ|
Слайд 5Для коротких записей утверждений используют символы :
принадлежит
не принадлежит
подмножество
пересечение
объединение
существует только
единственное
существует
любое,
всякое
Слайд 6Для коротких записей утверждений используют символы :
параллельны
не параллельны
перпендикулярны
скрещивающиеся
равносильны
следует
Слайд 9Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости
β; не лежащие в плоскости β.
2. Назовите прямые, лежащие в
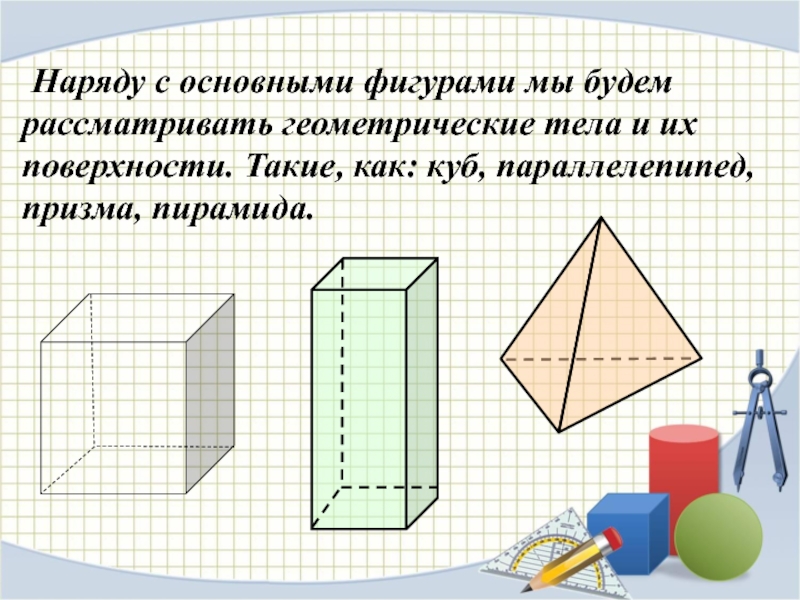
плоскости β; не лежащие в плоскости βСлайд 10 Наряду с основными фигурами мы будем рассматривать геометрические тела и
их поверхности. Такие, как: куб, параллелепипед, призма, пирамида.
Слайд 12В аксиомах стереометрии выражены основные свойства неопределяемых понятий: точки, прямой,
плоскости и расстояния.
Аксиома – это предложение не требующее доказательство.
Слайд 13Аксиома 1
Существует хотя бы одна прямая и хотя бы одна
плоскость. Каждая прямая и каждая плоскость есть не совпадающее с
пространством непустое множество точек.а
α
Для любой плоскости α и прямой а существует хотя бы одна не принадлежащая им точка.
Слайд 14Аксиома 2
Через любые две различные точки проходит одна и только
одна прямая.
Если прямые имеют по две общие точки, то эти
прямые совпадают: а = b Слайд 15Аксиома 3
Прямая, проходящая через две различные точки плоскости, лежит
в этой плоскости
А
В
α
Слайд 16Аксиома 4
Через три точки, не принадлежащие одной прямой,
проходит одна и только одна плоскость.
Если плоскости имеют три общие
точки, не принадлежащие одной прямой, то эти плоскости совпадают (α=β)Слайд 17Аксиом 5
Если две различные плоскости имеют общую точку, то
их пересечение есть прямая.
Две плоскости, пересечением которых является прямая
(α∩β=а), называются пересекающимися плоскостями.Слайд 18Аксиома 6
Для любых двух точек А и В имеется
неотрицательная величина, называемая расстоянием от А до В. Расстояние |АВ|
равно нулю в том и только в том случае, если точки А и В совпадают.А
В
А
В
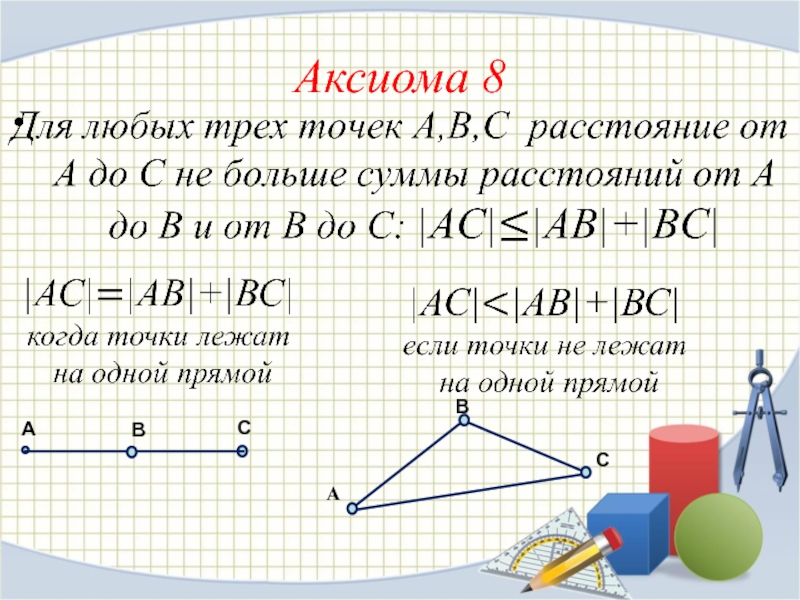
Слайд 19Аксиома 7
Расстояние от точки А до точки В равно расстоянию
от точки В до точки А: |АВ|=|ВА|
А
В
Слайд 21Аксиома 9
Для каждой плоскости выполняются известные из планиметрии аксиомы порядка,
подвижности плоскости и параллельных прямых
Из принятых выше аксиом вытекает, что
в каждой плоскости можно применять теоремы планиметрии. Например, в каждой плоскости выполняется теорема Пифагора, сумма углов любого треугольника равна 180°
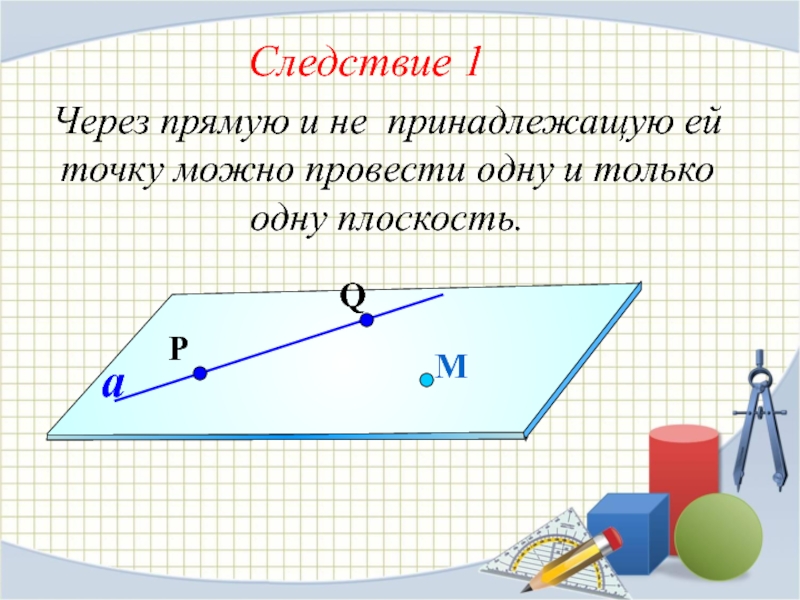
Слайд 22 Следствие 1
Через прямую и не принадлежащую ей
точку можно провести одну и только одну плоскость.
М
a
Слайд 24Через две пересекающиеся прямые можно провести одну и только одну
плоскость.
М
a
b
N
Следствие 2
Т
Слайд 26Определение:
Две прямые называются параллельными, если они лежат в одной плоскости
и не имеют общей точки.
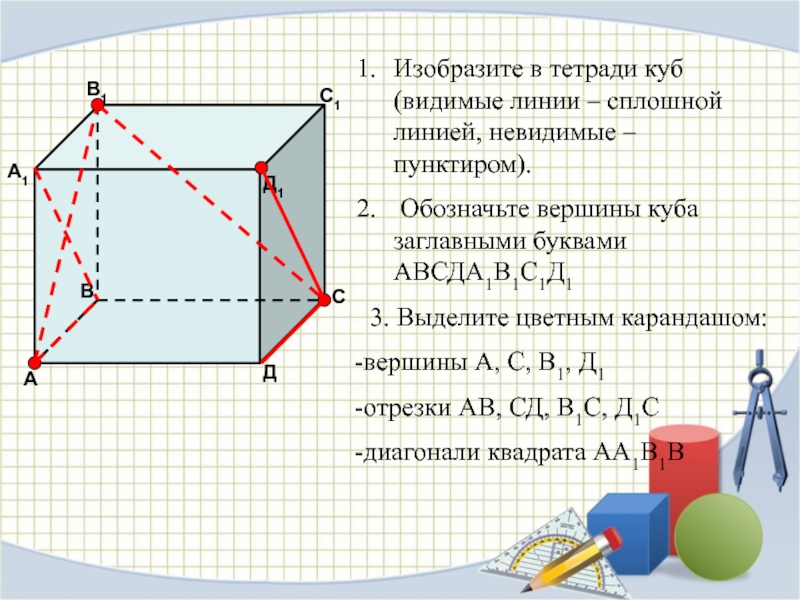
Слайд 29Изобразите в тетради куб (видимые линии – сплошной линией, невидимые
– пунктиром).
Обозначьте вершины куба заглавными буквами АВСДА1В1С1Д1
3. Выделите
цветным карандашом:вершины А, С, В1, Д1
отрезки АВ, СД, В1С, Д1С
диагонали квадрата АА1В1В
А
В
С
Д
Д1
С1
В1
А1
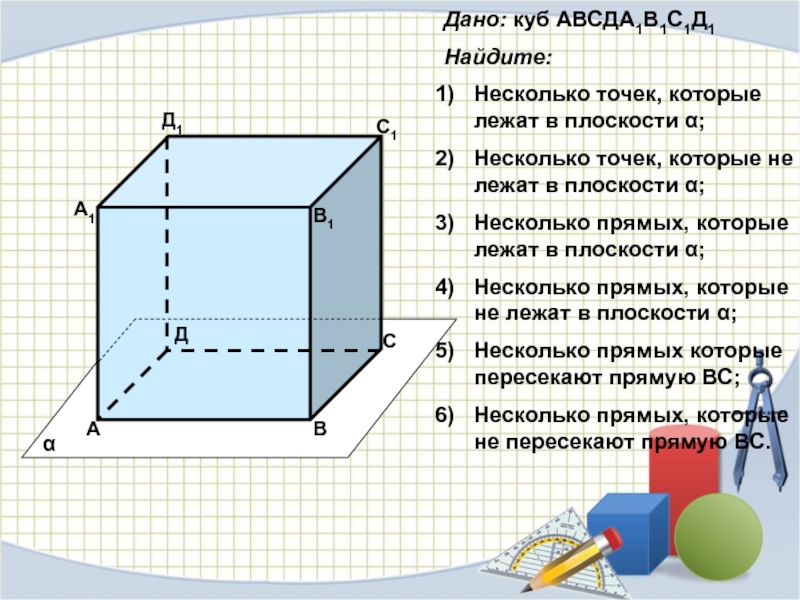
Слайд 30Дано: куб АВСДА1В1С1Д1
Найдите:
Несколько точек, которые лежат в плоскости α;
Несколько точек,
которые не лежат в плоскости α;
Несколько прямых, которые лежат в
плоскости α;Несколько прямых, которые не лежат в плоскости α;
Несколько прямых которые пересекают прямую ВС;
Несколько прямых, которые не пересекают прямую ВС.
Слайд 31А
В
С
Д
А1
В1
С1
Д1
α
Прямые АА1, АВ, АД проходят через точку А, но не
лежат в одной плоскости
Лежат ли прямые АА1, АВ, АД в
одной плоскости?Слайд 32Назовите плоскости, в которых лежат прямые
РЕ, МК, DB, AB, EC
Назовите
точки, лежащие в плоскостях АDB и DBC
P
E
A
B
C
D
M
K
Слайд 33P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
Назовите точки, лежащие в плоскостях DCC1 и BQC
Назовите плоскости, в
которых лежит прямая АА1
Слайд 34Задания
для самостоятельной работы:
Задание 1.
Запишите с помощью символов взаимное
расположение точек, прямых и плоскостей, изображенных на рисунке.
Слайд 35Задания
для самостоятельной работы:
Задание 2.
Дан куб ABCDA1B1C1D1 .
Запишите
с помощью символики ответы на вопросы:
а) По какой прямой пересекаются
плоскости:(ABC) и (AA1D1 );
(AA1B1) и (AA1D );
(BB1C1 ) и (CC1D1 ).
б) Каким плоскостям принадлежат точки: A, C1 , D ?
в) Принадлежит ли B1 плоскости:
1) (ABC) ; 2) (BB1C1 ) ; 3) (A1B1C1) ?