Раздел 1. Интерференция Лекция 1-2. Интерференция

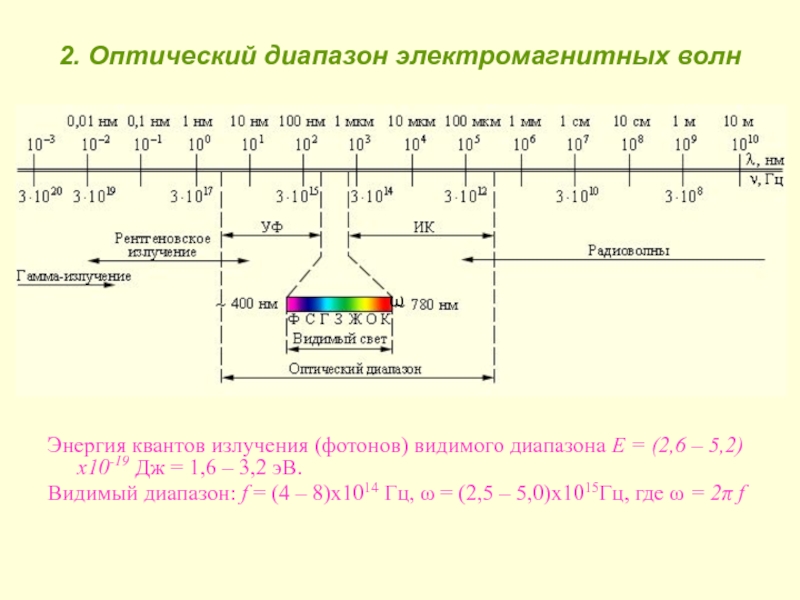
электромагнитных волн
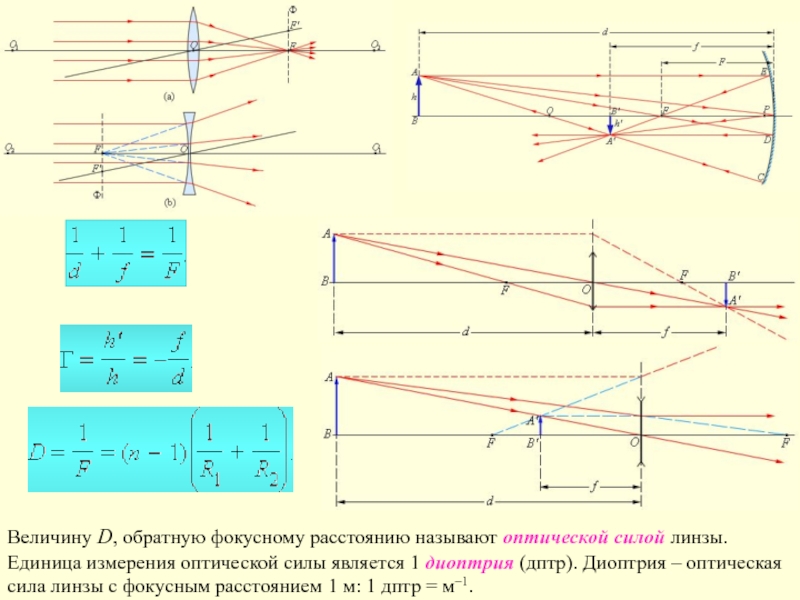
1.3. Геометрическая оптика
1.4. Явление интерференции
Интерференция плоских и сферических

волн
1.5. Базовая схема интерференции
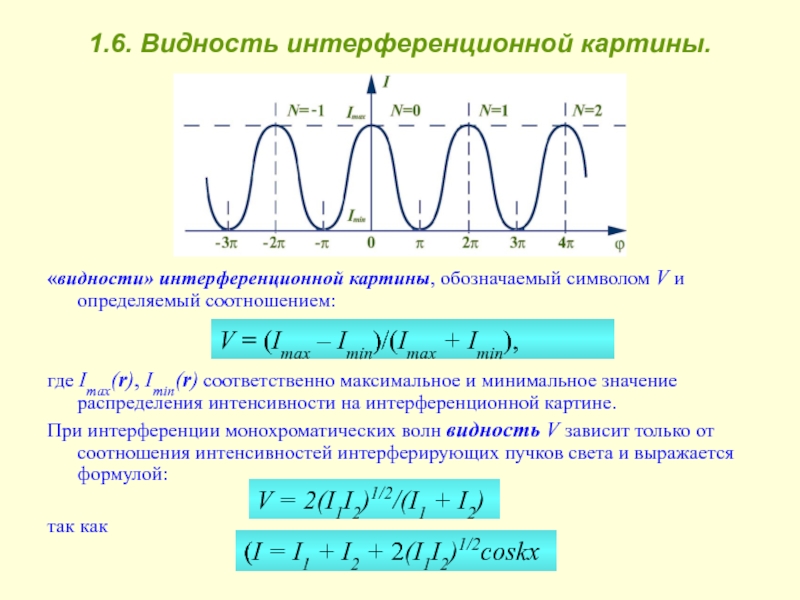
1.6. Видность интерференционной картины.

а также его взаимодействие с веществом. Учение о свете принято

делить на три части:
геометрическая или лучевая оптика, в основе которой лежит представление о световых лучах;
волновая оптика, изучающая явления, в которых проявляются волновые свойства света;
квантовая оптика, изучающая взаимодействие света с веществом, при котором проявляются корпускулярные свойства света.

rotrotВ = graddivВ — ΔВ, где

ΔВ — ε0μ0 д2В/дt2

= 0, ΔЕ — ε0 μ0 д2Е/дt2 = 0

Подставим : ,




Обозначим (k2/ε0μ0) как ω2. Решение этих уравнений будет
и

Общее комплексное решение уравнений будет
k = 2π/λ – это волновое число, определяемое длиной волны λ = 2πс/ω; (с – скорость света в вакууме).
Амплитуда, создаваемой цилиндрической волны, убывает обратно пропорционально r1/2,
а амплитуда сферической волны, убывает обратно пропорционально r.

перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения

волны
Электромагнитные волны распространяются в веществе с конечной скоростью υ = (ε0εμ0μ)-1/2 ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
с = (ε0μ0)-1/2 = 2,997924х108 м/с

полей. Эти процессы идут одновременно, и электрическое и магнитное поля

выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм.


Отсюда следует, что в электромагнитной волне модули индукции магнитного поля B и напряженности электрического поля E в каждой точке пространства связаны соотношением


4. Поток энергии в электромагнитной волне можно задавать с помощью вектора I направление которого совпадает с направлением распространения волны, .
Этот вектор называют вектором Умова-Пойнтинга (1885 г.).

Е = (2,6 – 5,2)х10-19 Дж = 1,6 – 3,2

эВ.
Видимый диапазон: f = (4 – 8)х1014 Гц, ω = (2,5 – 5,0)х1015Гц, где ω = 2π f

ω

на границе двух прозрачных сред
Закон прямолинейного распространения света.
Закон отражения

света
Закон преломления света

n называют относительным показателем преломления второй среды относительно первой: n = n2/n1.
Полное внутреннее отражение

измерения оптической силы является 1 диоптрия (дптр). Диоптрия – оптическая

сила линзы с фокусным расстоянием 1 м: 1 дптр = м–1.

Явление перераспределения в пространстве интенсивности электромагнитного поля, представляющего собой сумму

двух монохроматических волн одной частоты, в зависимости от их разности фаз называется интерференцией.

I2 интенсивность суммарной волны получаем аналогично:

если
xmax = ± mlλ0/d (m = 0, 1,

2, …),
а минимумы – в случае, если
xmin = ± (m + ½)lλ0/d (m = 0, 1, 2, …),
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно
х = lλ0/d.

оптической разностью хода
 = s2 – s1.
s22 = l2 + (x + d/2)2;
s12 = l2 + (x - d/2)2,
Откуда s22 – s12 = 2xd,
 = s2 - s1 = 2xd/(s2 + s1).
Из условия l>>d следует, что s1 + s2  2l, поэтому Δ = xd/l.
Максимумы будут при  = mλ0, а минимумы при  = (m + ½)λ0.

m) и является постоянной для данных l, d и 0.

И x обратно пропорционально d; следовательно, при большом расстоянии между источниками, например при d  l, отдельные полосы становятся неразличимыми. Для видимого света 0  10-7 м, поэтому четкая, доступная для визуального наблюдения интерференционная картина имеет место при l >> d (это условие и принималось при расчете). По измеренным значениям l, d в х, можно экспериментально определить длину волны света. Интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу. Главный максимум, соответствующий m = 0, проходит через точку О. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы (минимумы) первого (m = 1), второго (m = 2) порядков и т. д.

и определяемый соотношением:


где Imax(r), Imin(r) соответственно максимальное и минимальное

значение распределения интенсивности на интерференционной картине.
При интерференции монохроматических волн видность V зависит только от соотношения интенсивностей интерферирующих пучков света и выражается формулой:

так как

V = (Imax – Imin)/(Imax + Imin),

V = 2(I1I2)1/2/(I1 + I2)

(I = I1 + I2 + 2(I1I2)1/2coskx