газа. Уравнение состояния.
Законы: Авогадро, Дальтона, Паскаля.
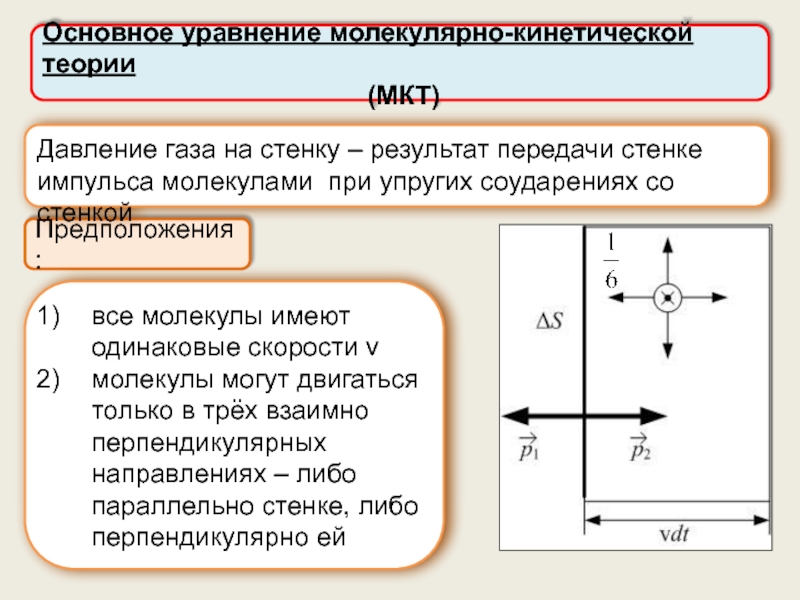
Основное уравнение молекулярно-кинетической теории (МКТ).
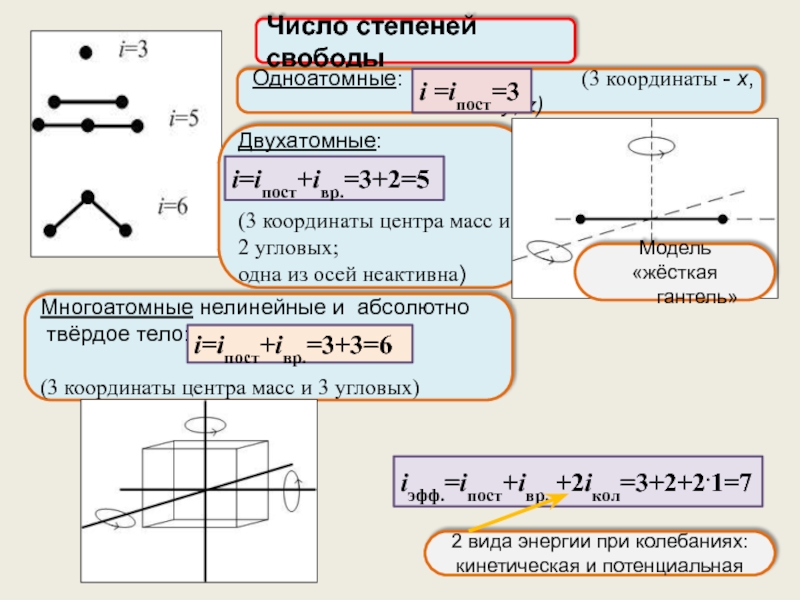
Теорема о равнораспределении энергии по степеням свободы.
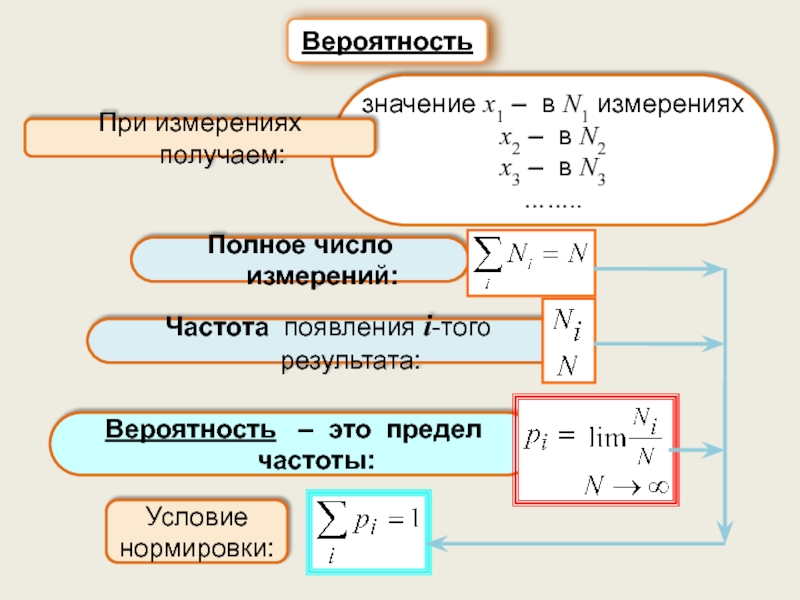
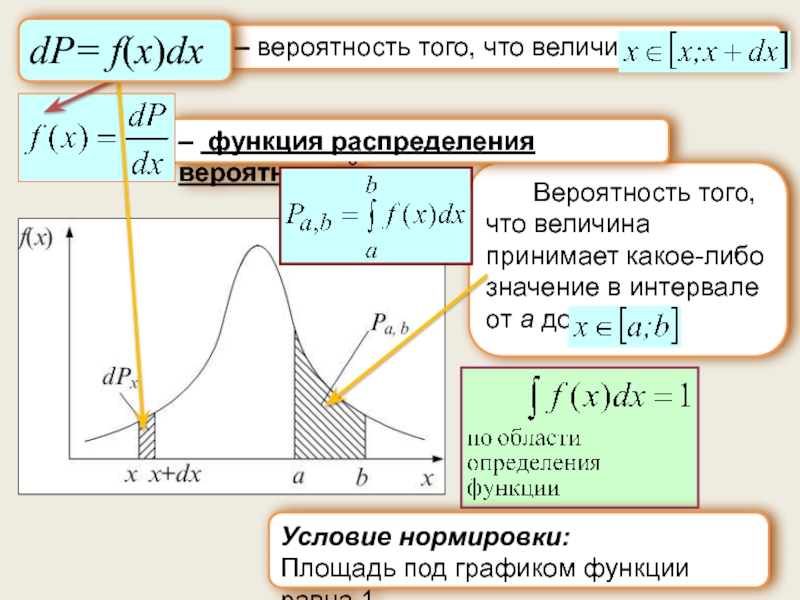
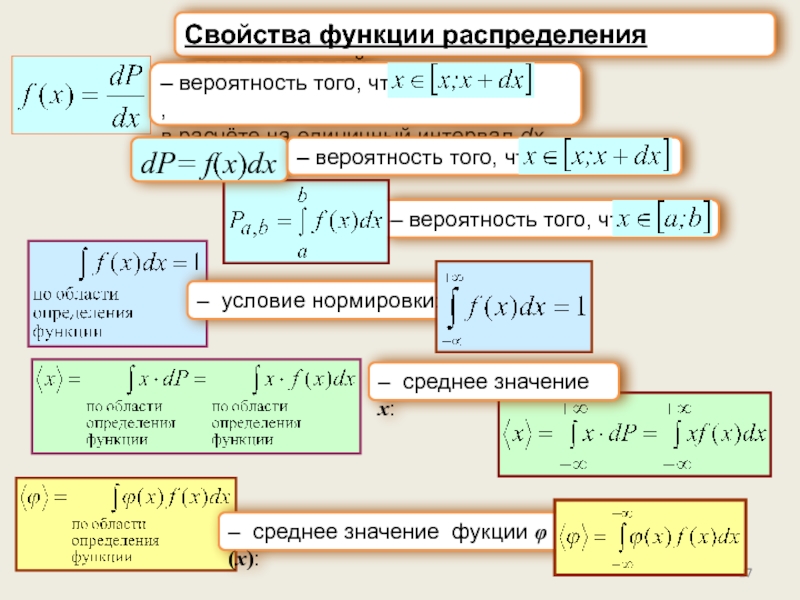
Понятие о классической статистике. Вероятность. Законы сложения и умножения вероятностей.
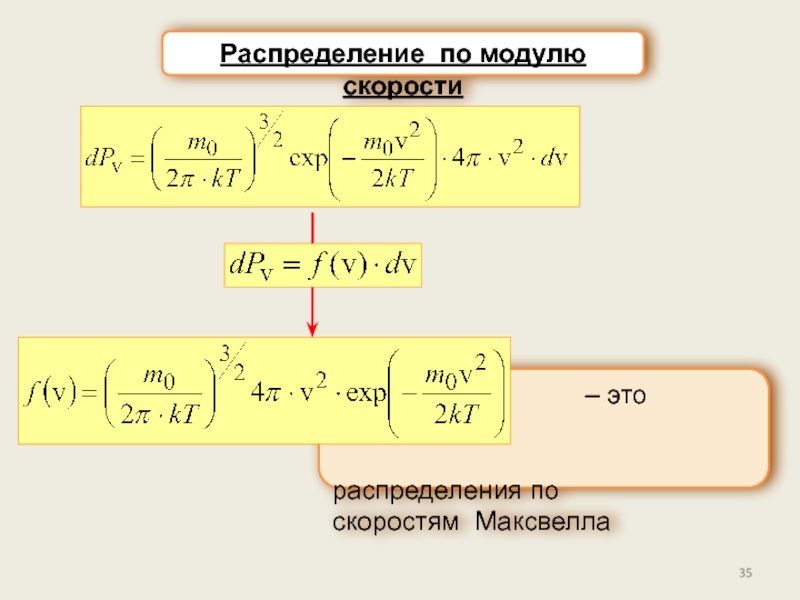
Закон распределения по скоростям Максвелла.
а) Постановка задачи.
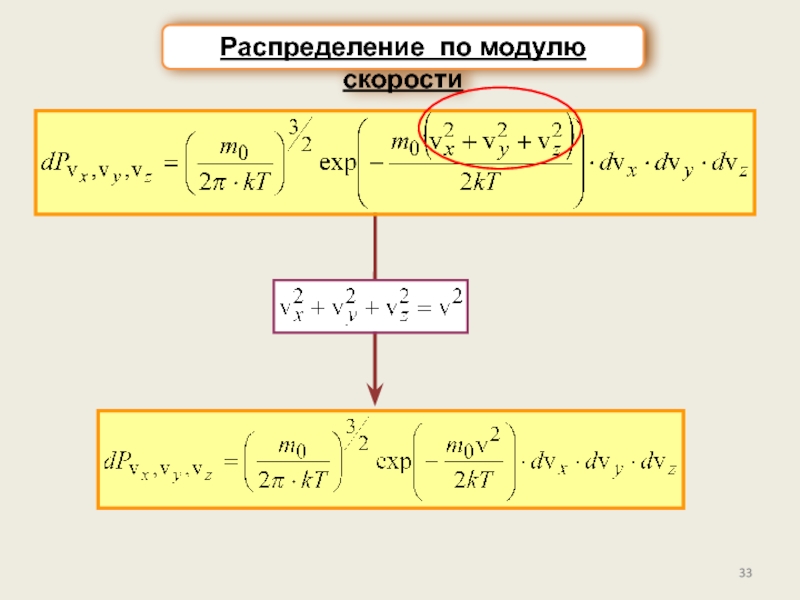
б) Распределение по компонентам (проекциям) скоростей.
в) Распределение по модулю скорости.
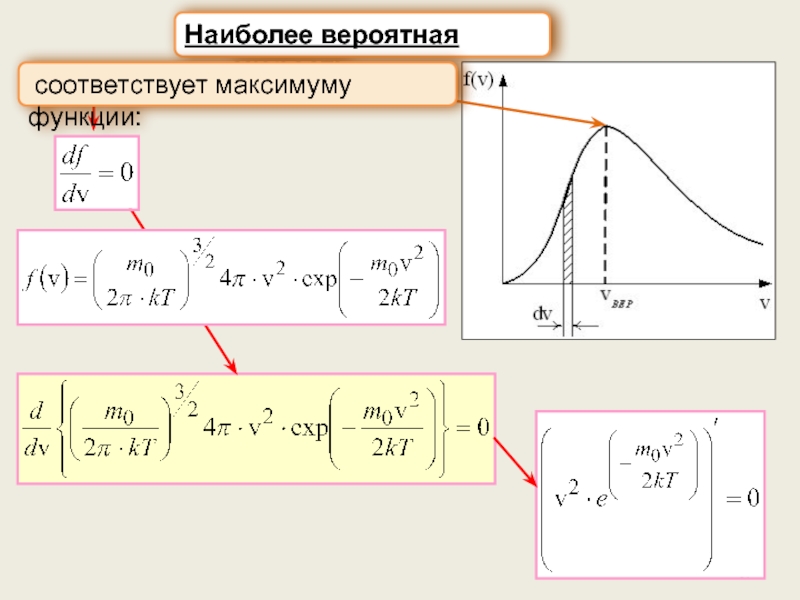
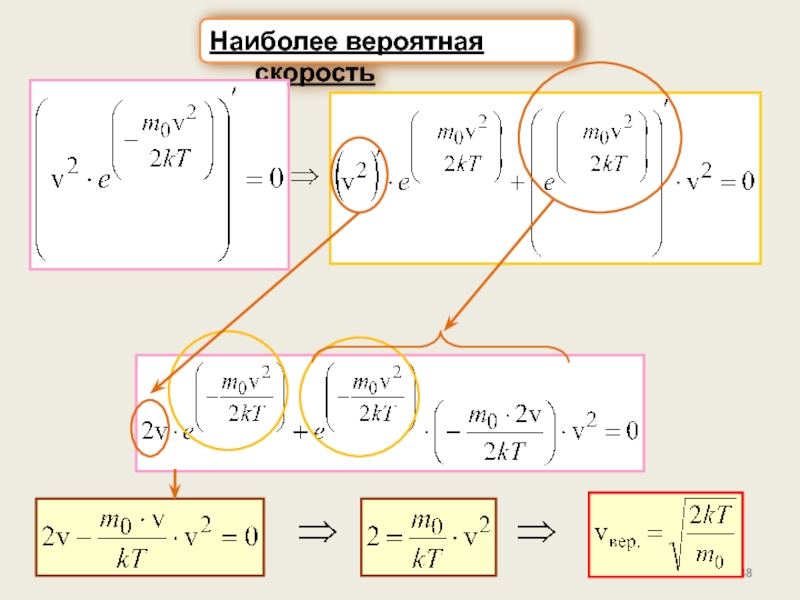
г) Характерные скорости: наиболее вероятная, средняя
арифметическая, средняя квадратичная.
д) Экспериментальная проверка распределения Максвелла: опыт Штерна.
е) Распределение по энергиям.
8. Газ в поле тяготения. Барометрическая формула. Распределение Больцмана
План
































![Раздел II Статистическая физика Термодинамика . dN – число молекул с энергиями E∈[E ;E+dE] – доля . dN – число молекул с энергиями E∈[E ;E+dE] – доля молекул с такими энергиями(вероятность, что E∈[E](/img/thumbs/96846293406d9aab05d25bd8b260aa00-800x.jpg)




























