Слайд 1
Различные способы решения задач на
смеси, сплавы,
растворы
Слайд 2 Задачи на смеси, сплавы, растворы вызывают у учащихся общеобразовательных классов
затруднения. Самостоятельно справиться с ними могут немногие. Задачи данного типа,
ранее встречающиеся практически только на вступительных экзаменах в ВУЗы и олимпиадах, сейчас включены в КИМы для подготовки и проведения экзамена по математике за курс основной школы. Эти задачи, имеющие практическое значение, являются также хорошим средством развития мышления учащихся. Поэтому на сегодняшний день тема решений таких задач является актуальной.
Цель работы: помочь учащимся 11 классов успешно сдать выпускной экзамен.
Слайд 3
Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
Все
получающиеся сплавы или смеси однородны.
При решении этих задач считается,
что масса смеси нескольких веществ равна сумме масс компонентов.
Процент - одна сотая любого вещества.
Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.
Это отношение может быть выражено либо в дробях, либо в процентах.
Сумма концентраций всех компонент, составляющих смесь, равна единице.
Слайд 4типы задач
на вычисление концентрации;
на вычисление количества чистого
вещества в смеси (или сплаве);
на вычисление массы смеси (сплава).
Слайд 5Способы решения задач
с помощью таблиц;
с помощью схемы;
по правилу креста;
старинным
арифметическим способом;
алгебраическим способом;
с помощью графика;
с помощью формулы.
Слайд 6
Рассмотрим несколько задач и решим их различными способами.
Слайд 7
Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200
г 70 % -го раствора уксусной кислоты, чтобы получить 8
% раствор уксусной кислоты?
Решение: 1 способ – с помощью таблицы:
Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение :
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
Слайд 8
2 способ - с помощью схемы:
Пусть в сосуд долили
х литров воды.
Получаем схему:
Уксусная Уксусная
кислота кислота
70% + х литров 8%
воды
200 г. (200 + х) г.
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
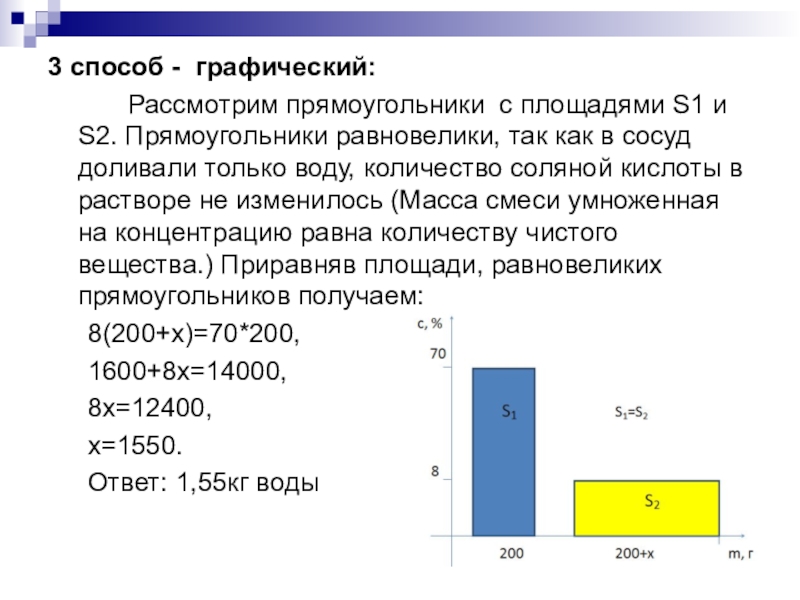
Слайд 93 способ - графический:
Рассмотрим прямоугольники с площадями S1 и S2.
Прямоугольники равновелики, так как в сосуд доливали только воду, количество
соляной кислоты в растворе не изменилось (Масса смеси умноженная на концентрацию равна количеству чистого вещества.) Приравняв площади, равновеликих прямоугольников получаем:
8(200+х)=70*200,
1600+8х=14000,
8х=12400,
х=1550.
Ответ: 1,55кг воды
Слайд 10
Задача 2: Смешали некоторое количество 15–процентного раствора некоторого вещества с
таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет
концентрация получившегося раствора?
Решение: 1 способ – с помощью формулы.
Пусть количество каждого из растворов было V.
Тогда количество сухого вещества в первом растворе 0,15V , а во втором – 0,19V. После того как растворы смешали их общий объем стал 2V, а количество сухого вещества в смеси стало 0,15V+0,19V. Концентрация раствора равна:
Таким образом, концентрация полученного раствора равна:
Ответ: 17.
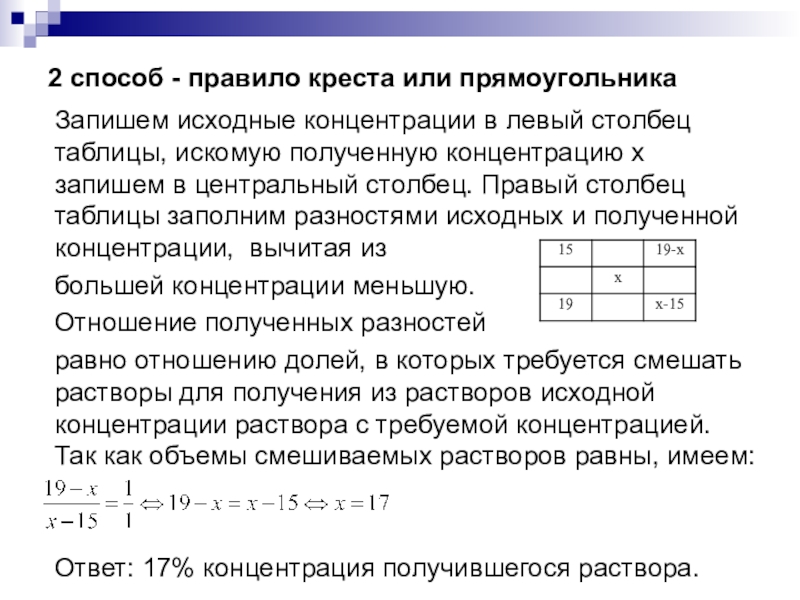
Слайд 112 способ - правило креста или прямоугольника
Запишем исходные концентрации в
левый столбец таблицы, искомую полученную концентрацию х запишем в центральный
столбец. Правый столбец таблицы заполним разностями исходных и полученной концентрации, вычитая из
большей концентрации меньшую.
Отношение полученных разностей
равно отношению долей, в которых требуется смешать растворы для получения из растворов исходной концентрации раствора с требуемой концентрацией. Так как объемы смешиваемых растворов равны, имеем:
Ответ: 17% концентрация получившегося раствора.
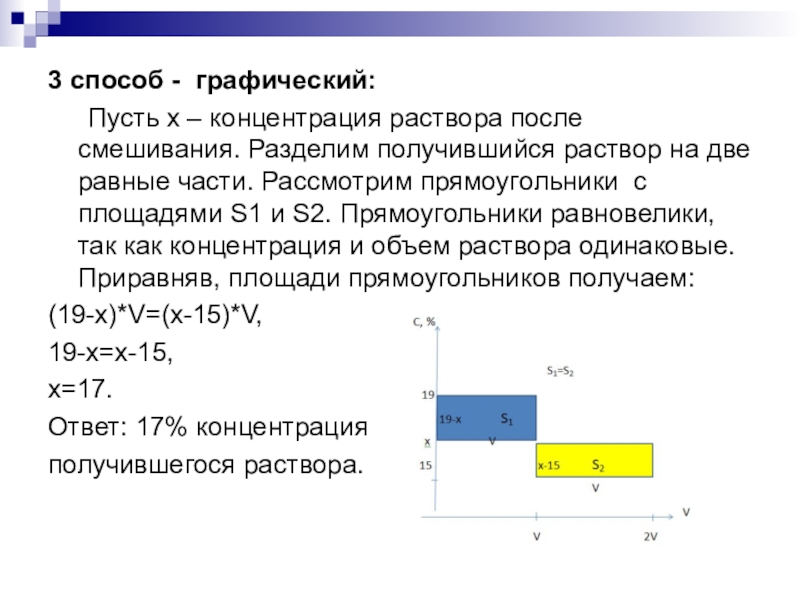
Слайд 123 способ - графический:
Пусть x – концентрация раствора после смешивания.
Разделим получившийся раствор на две равные части. Рассмотрим прямоугольники с
площадями S1 и S2. Прямоугольники равновелики, так как концентрация и объем раствора одинаковые. Приравняв, площади прямоугольников получаем:
(19-x)*V=(x-15)*V,
19-x=x-15,
x=17.
Ответ: 17% концентрация
получившегося раствора.
Слайд 13Задача 3: Сначала приготовили 25%-ый водный раствор поваренной соли. Затем
одну треть воды выпарили. Найдите концентрацию получившегося раствора.
Решение – с
помощью схемы(наиболее простой способ решения этой задачи):
До выпаривания:
25% 25% 25% 25%
После выпоривания:
% % %
Сейчас соль стала составлять третью часть всего
раствора, т.е. 100% : 3 = %
Ответ: %.
Слайд 14
Задача 4: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором
и получили 600 г 15%-го раствора. На сколько граммов масса
первого раствора меньше массы второго?
Решение: 1 способ – алгебраический.
Обозначим x массу первого раствора,
тогда масса второго (600 - x).
Составим уравнение:
0,3x + 0,1* (600 - x) = 600 * 0,15,
0,3х + 60 - 0,1х = 90,
0,2х = 30,
x = 150.
600 - 150 = 450 г; 450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Слайд 15
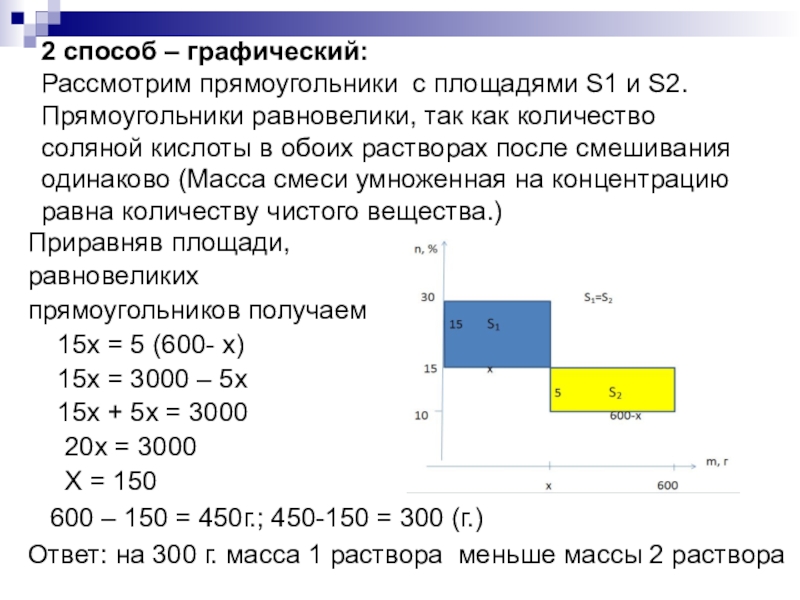
2 способ – графический:
Рассмотрим прямоугольники с площадями S1 и S2.
Прямоугольники равновелики, так как количество соляной кислоты в обоих растворах
после смешивания одинаково (Масса смеси умноженная на концентрацию равна количеству чистого вещества.)
Приравняв площади,
равновеликих
прямоугольников получаем
15x = 5 (600- x)
15х = 3000 – 5х
15х + 5х = 3000
20х = 3000
Х = 150
600 – 150 = 450г.; 450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Слайд 163 способ – с помощью схемы:
Пусть x – масса 1
раствора. Получим схему:
30x+10(600-x)=15*600,
30x+6000-10x=9000,
20x=3000,
X=150(грамм)- масса первого раствора
600 – 150
= 450г.- масса второго раствора
450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
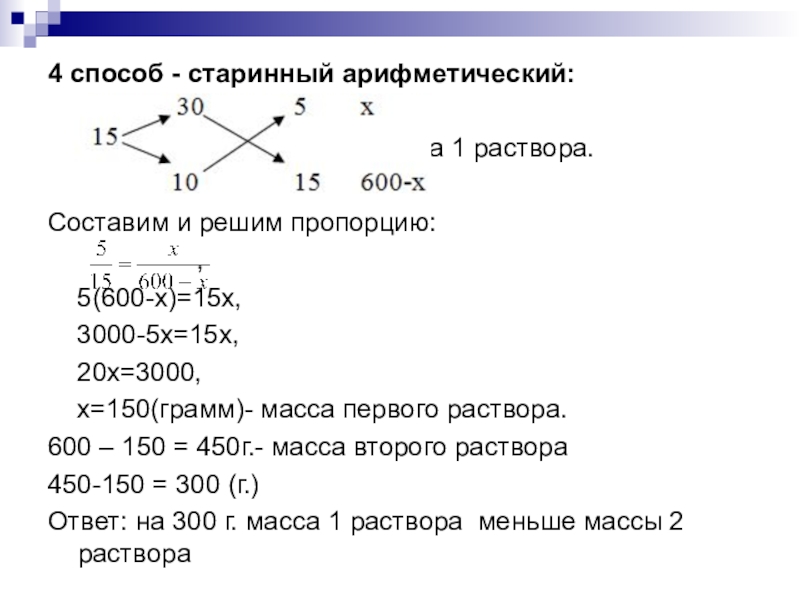
Слайд 174 способ - старинный арифметический:
, где x масса 1 раствора.
Составим
и решим пропорцию:
,
5(600-x)=15x,
3000-5x=15x,
20x=3000,
x=150(грамм)- масса первого раствора.
600 – 150 = 450г.- масса второго раствора
450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Слайд 18Задача 5: Первый сплав содержит 10% меди, второй – 40%
меди. Масса второго сплава больше массы первого на 3 кг.
Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение: 1 способ – старинный арифметический:
Пусть масса первого сплава равна m кг, тогда масса второго сплава m+3 кг.
Заполним схему:
Отношение полученных масс равно отношению
долей, в которых требуется сплавлять исходные
сплавы. Поэтому кг.
Тогда масса второго сплава равна 6 кг, а масса третьего сплава равна 9 кг.
Ответ: 9.
Слайд 192 способ – с помощью схемы:
Пусть m кг масса
1 сплава. Тогда схема для решения такой задачи имеет вид:
Составим
и решим уравнение:
10m+40(m+3)=30*(2m+3),
10m+40m+120=60m+90,
-10m=-30,
m=3(кг) – масса 1 сплава.
Тогда масса второго сплава равна 6 кг, а масса третьего сплава равна 9 кг.
Ответ: 9.
Слайд 20Задача 6. Имеется два сплава меди и свинца. Один сплав
содержит 15% меди, а другой 65% меди. Сколько нужно взять
каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение: 1 способ - с помощью схемы.
0,15х+0,65*(200-х)=0,3*200,
0,15х+130-0,65х=60,
-0,5х=-70,
х=140.
Ответ : надо взять140г. первого сплава и 60г. второго сплава.
Слайд 212 способ - алгебраический.
Пусть первого сплава было x грамм, а
второго y грамм. Тогда их масса равна x+y=200, а концентрация
равна 0,15x+0,65y=0,3*200. Получаем систему уравнений:
Ответ :надо взять140г. первого сплава и 60г. второго сплава.
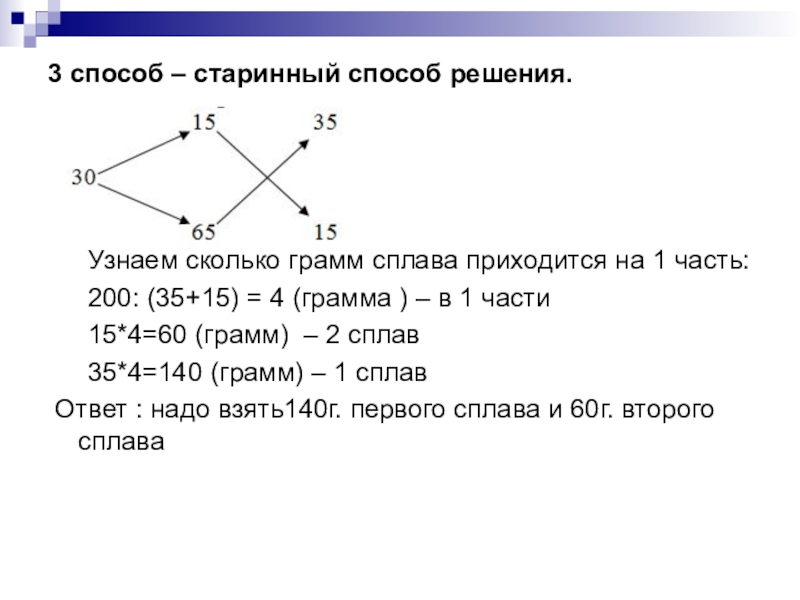
Слайд 223 способ – старинный способ решения.
Узнаем сколько грамм сплава
приходится на 1 часть:
200: (35+15) = 4 (грамма ) –
в 1 части
15*4=60 (грамм) – 2 сплав
35*4=140 (грамм) – 1 сплав
Ответ : надо взять140г. первого сплава и 60г. второго сплава
Слайд 23Заключение.
В ходе рассмотрения способов решения
задач на смеси, сплавы, растворы мы увидели красоту, сложность и
притягательность данных способов.
Выбор способа решения зависит от конкретной задачи и от умения решающего.
Слайд 24«Ныне и всяк лучший воин
Ону науку знать достоин»...
Леонтий Филиппович
Магницкий (1669—1739)
Слайд 25Список литературы:
Дмитрий Гущин. Математика.
ЕГЭ – 2013: экспресс-курс для
подготовки к экзамену.
Учительская
газета. Издательский дом «Комсомольская правда». Москва. 2013
Решу ЕГЭ. Образовательный портал
для подготовки к экзаменам. http://reshuege.ru/test?theme=88
HYPERLINK http://festival.1september.ru/