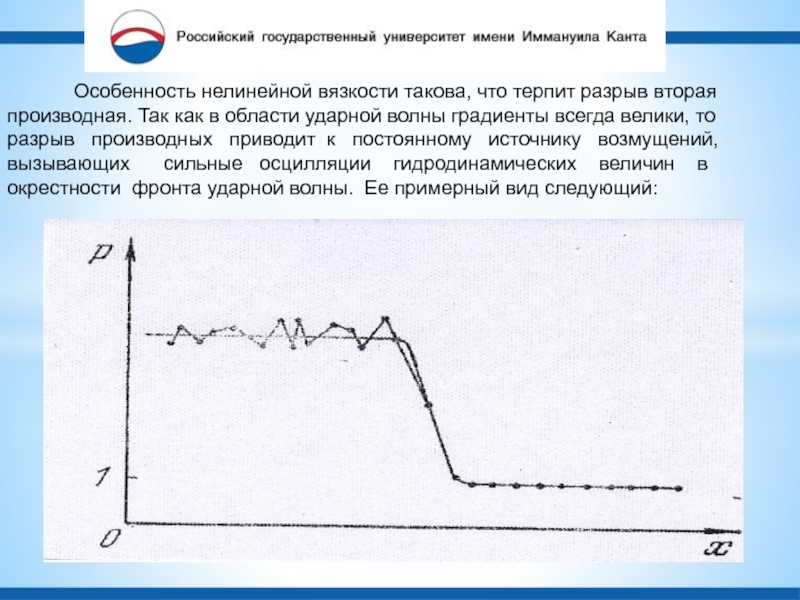
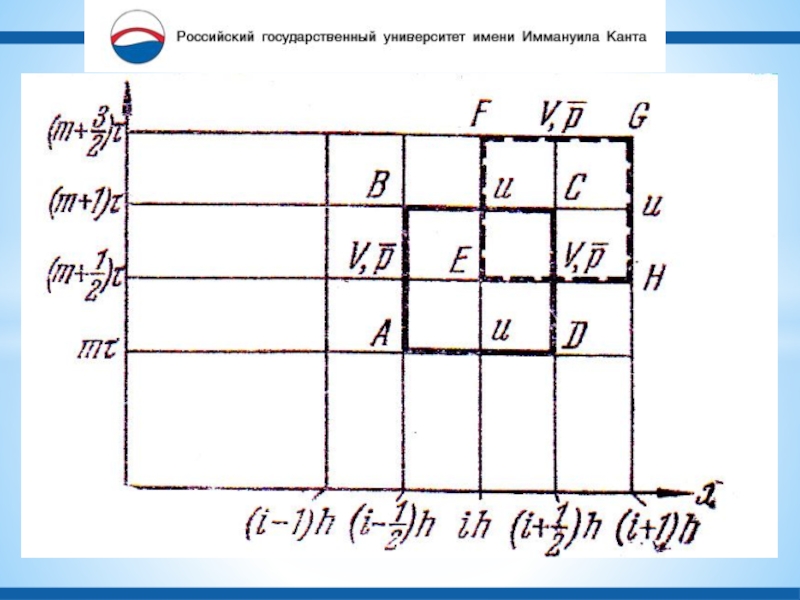
аспекта:
1) методы построения разностных схем;2) обоснование выбранной разностной схемы.
Большинство задач являются нелинейными, а теория разностных методов развита в основном для линейных задач
В газовой динамике мы имеем дело, вообще говоря, с
разрывными решениями интегро-дифференциальных
уравнений.
Понятие сходимости разностной схемы существенно
зависит от класса решений законов сохранения.
Норма близости двух обобщенных (разрывных) решений
является слабой (норма пространства )
.