Линейная дискриминантная функция Фишера

нормальном распределении данных.

Пусть имеется обучающая выборка: x1, x2, ... xN

, где:

N1 элементов из множества X1
N2 элементов из множества X2

Общее число элементов N = N1 + N2

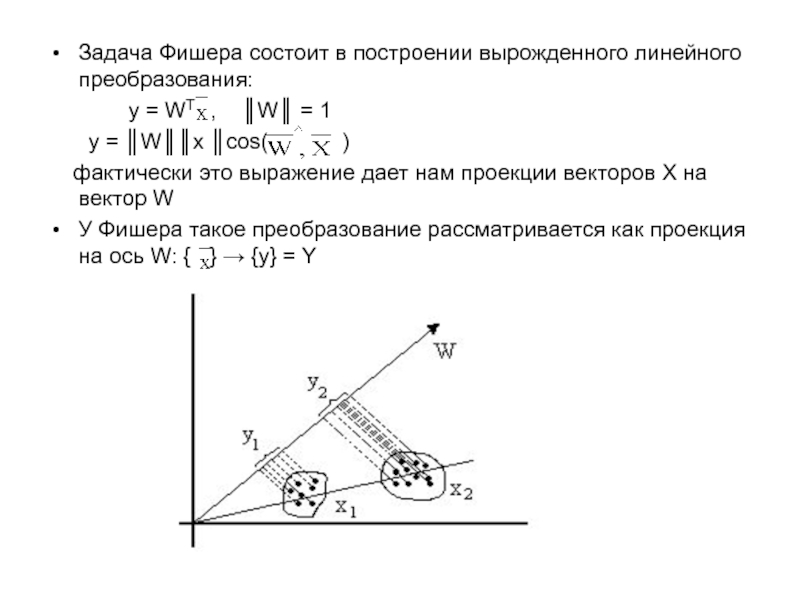
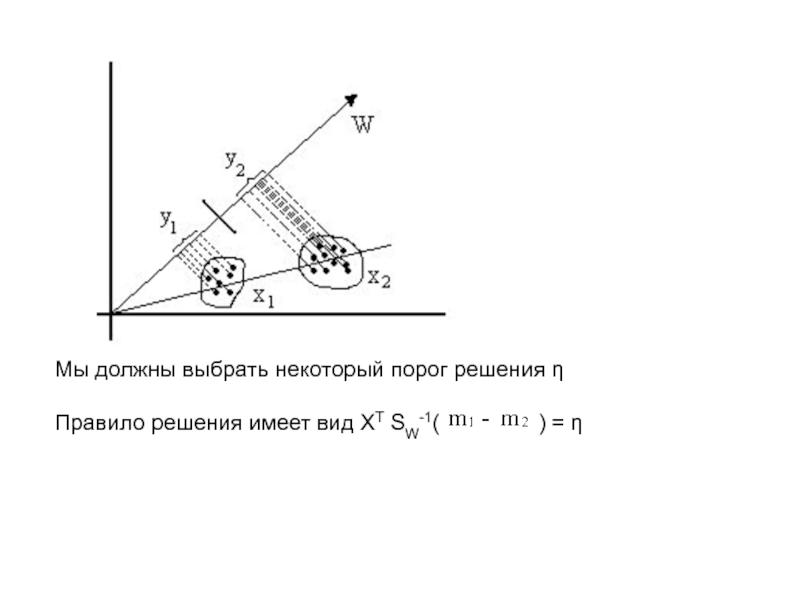
Задача состоит в построении разделяющей функции для двух классов:

X1 = {xi} i=1..N1 X2 = { } j=1..N2

, ║W║ = 1
y = ║W║║x ║cos(

)
фактически это выражение дает нам проекции векторов X на вектор W
У Фишера такое преобразование рассматривается как проекция на ось W: { } → {y} = Y

были наиболее разнесены (то есть, удалены друг от друга).

Критерий разнесения

может быть выбран разным.

Исходить будем из следующих параметров: для каждой выборки определим среднее значение:

mi = xi


= yi = WTxi = WT{ x} = WT mi


Далее мы строим | - |:

| - | = WT( ) - это скалярная величина

(y - )2 - разброс внутри

класса


= + - суммарный разброс

Разброс внутри класса – это нечто вроде дисперсии, только ненормированной.

- средняя дисперсия выборки в Y.

определяем матрицу разброса внутри класса:

= (WTx

- WT mi)2 = WT (x - mi) WT(x - mi) =


= WT (x - mi)(x - mi)T W = WT [ (x - mi)(x - mi)T]W =

=WT Si W

Si – матрица разброса внутри Xi.

S2 = SW - суммарная матрица разброса для всех результатов.

+ = WT SW W

Таким же образом можно представить ( - )2:

( - )2 = (WT - WT )2 = WT( )WT( ) =

= WT( )( )T W = WT SB W

Матрица SB - матрица разброса между классами

) =

Далее стоит задача оптимизации данного отношения (мы

должны его максимизировать).

Рассмотрим свойства матрицы SB:

SB = ( )( )T

1. это квадратная матрица размерности n × n
2. произведение этой матрицы на произвольный вектор

SB = ( )( )T = С( )
C - скаляр
дает вектор, который по направлению совпадает с разностью
( )

представить ее в виде ddT:

d1d1 d1d2 ... d1dn
d2d1 d2d2 ...

d2dn
. = ( ) .
.
dnd1 dnd2 ... dndn

- матрица вырожденная и ранг ее равен единице.

SB W - λ WT SW W,
где λ -произвольная

константа
Эта функция зависит от W
Мы должны найти производную этой функции по вектору :

= 2 SB - 2 λ SW = 0


= 2A - такое правило существует, его легко
доказать

Получаем следующее:
SB W - λ SW W

λ SW , отсюда окончательно имеем:

=

SW-1 ( ) .

Так как вектор произвольной длины, положим =1, тогда имеем :

= SW-1 ( ).

Соответственно линейный дискриминант Фишера получается в следующем виде:

y = T = XTW = SW-1( ) - это проекция вектора на ось W

XT SW-1( )

= η

пропорциональна суммарной матрице ковариации и соответственно для случая нормального распределения

исходных данных дискриминант Фишера дает результат такой же, как и байесовская линейная дискриминантная функция:

XT Σ-1(M1 – M2) + C1 ... ≥ C2