Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разработка управленческих решений
Содержание
- 1. Разработка управленческих решений
- 2. Типы неопределенностейНеопределенности природыНеопределенности целейНеопределенности противника
- 3. Неопределенности природы Принятие решений в условиях
- 4. Принятие решений в условиях неопределенности природы
- 5. Принятие решений в условиях неопределенности природы
- 6. Принятие решений в условиях неопределенности природыВ
- 7. Матрица решений
- 8. Вектор результатов
- 9. Вектор результатов Его роль –
- 10. ПримерПланирование производственных мощностейММ – малые мощности; СМ – средние мощности; КМ – крупные мощности
- 11. Принимать решения, как правило, сравнительно легко. Все
- 12. Позиции ЛПРОптимистическаяПессимистическаяПозиция компромиссаПозиция нейтралитета
- 13. Пессимистическая позиция ЛПР
- 14. Вектор результатов firfir=max fij
- 15. Классические критерии принятия решений
- 16. Классические критерии ПРМинимаксный критерий, или критерий Вальда
- 17. Оценочная функция -
- 18. Правило выбора (MM)Матрица решений дополняется еще
- 19. ЗамечаниеВыбранные таким образом варианты полностью исключают риск:
- 20. Пример
- 21. Применение ММ-критерияо возможности появления внешних
- 22. Критерий Сэвиджа (S)||Δij || =Savage
- 23. Критерий СэвиджаРиск, или остаток||Δij || = max
- 24. Критерий Сэвиджа||Δij || =
- 25. Критерий Сэвиджа Zs=min max (max
- 26. Правило выбораЛюбой элемент матрицы решений вычитается
- 27. Критерий Гурвица (HW)ZHW=max[c*min fij +(1-c)*max fij]
- 28. Правило выбораМатрица решений дополняется столбцом, содержащимсредневзвешенную
- 29. Критерий Гурвица (HW)
- 30. Применение HWо вероятностях появления событий αj ничего не известно;реализуется малое количество решений;допускается некоторый риск
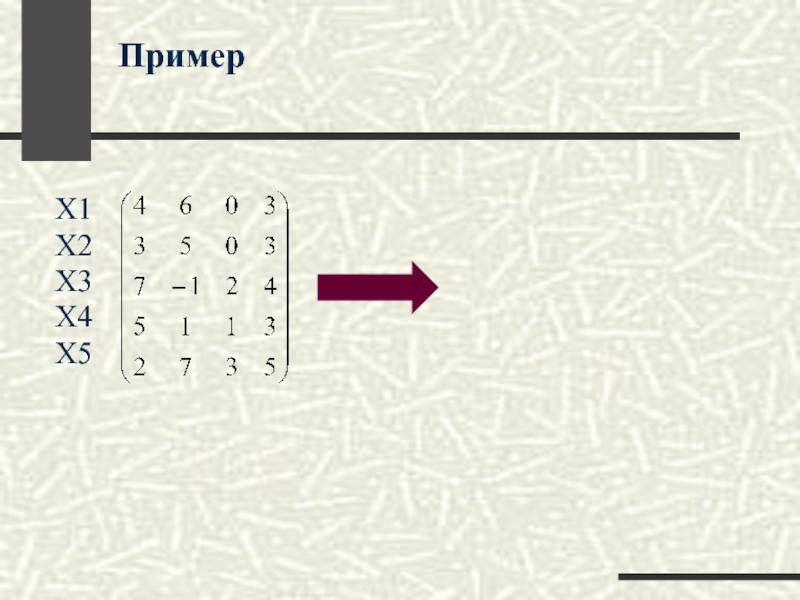
- 31. X1X2X3X4X5Пример
- 32. Неопределенности природыВ условиях полной неопределенности решение определяется
- 33. Классические критерии ПРКритерий Байеса-Лапласа (BL) αj →
- 34. Матрица решенийpj p1
- 35. Правило выбора Матрица решений дополняется еще одним
- 36. Применение BLвероятности появления состояний αj известны и
- 37. Позиция ЛПР (BL)Исходная позиция ЛПР, применяющего критерий
- 38. Классические критерии ПР (пример)Планирование производственных мощностейММ –
- 39. Пример
- 40. Критерий Гермейера (G)
- 41. Критерий Гермейера (G)Правило выбора: Матрица решений
- 42. Слайд 42
- 43. Планирование эксперимента в условиях неопределенностиПредстоит принять решение
- 44. Условия полной неопределенности
- 45. Дополнительная информация
- 46. ЭкспериментРассмотрим сначала случай “идеального” эксперимента ε, приводящего
- 47. Эксперимент? ||fij||, вероятности Р(αj)=pjОбозначим
- 48. Cредний выигрыш без εБез проведения эксперимента ε
- 49. Матрица решений
- 50. ЭкспериментПри αj выигрыш будет равен максимальному результату
- 51. Эксперимент Но нужно заранее решить, следует проводить эксперимент или нет. Поэтому средний выигрыш =
- 52. ЭкспериментСредний выигрыш с учетом стоимости идеального эксперимента
- 53. Эксперимент>
- 54. Экспериментсost< для любого i,или сost
- 55. Идеальный эксперимент ε затраты на его
- 56. Пример100*1/2 +120*1/3+160*1/6 – 100 = 16,66Cost
- 57. Матрица остатков ||Δij||0*1/2+20*1/3+60*1/6=16,66cost
- 58. Эксперимент В случае, когда эксперимент
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Пример Некоторый объект надо подвергнуть проверке
- 63. Пример Варианты решения: Х1 - полная проверка;Х2 - минимальная проверка;Х3 - отказ от проверки.
- 64. ПримерСостояния αj:
- 65. ПримерРезультаты fij: затраты на проверки и устранение
- 66. Примерcost< - 47/3 + 64/3 =17/3
- 67. Пример Является ли целесообразным “идеальный” эксперимент, стоимость которого cost=2? 5,24,55,0
- 68. Неидеальный экспериментРассмотрим неидеальный эксперимент ε, который не
- 69. Обозначим условную вероятность события Bl в условиях
- 70. - это условные вероятности событий αj, подсчитываются
- 71. Рассмотрим предыдущий пример с неидеальным экспериментом, который
- 72. РешениеВычислим апостериорные вероятности по формуле Байеса:
- 73. Решение4,9565,3955,394
- 74. Функции управления Для управленцев различного концептуального
- 75. Концептуальный уровень иерархии управления «Исполнитель» Исполнение
- 76. «Администратор» Руководство группой исполнителей или небольшими отделами
- 77. «Руководитель звена отрасли» Руководство крупной организацией, определение
- 78. «Высшее руководство» Определение политики и выбор стратегии
- 79. Основные типы задач принятия решений в условиях неопределенности
- 80. Составляюшие и источники риска в управленииРискИндивидуальныйСитуационный
- 81. Источники индивидуального рискаИнициатива (авантюризм, честолюбие, эгоизм, стремление
- 82. Источники ситуационного рискаВремя (дефицит времени на принятие
- 83. ЛПР должно руководитьОбеспечение наименьшего уровня риска требует
- 84. Понятие рационального выбора.Основные типы неопределенностей, встречающихся при
- 85. Слайд 85
- 86. Слайд 86
- 87. Скачать презентанцию
Типы неопределенностейНеопределенности природыНеопределенности целейНеопределенности противника
Слайды и текст этой презентации
Слайд 2Типы неопределенностей
Неопределенности природы
Неопределенности целей
Неопределенности противника
Слайд 3Неопределенности природы
Принятие решений в условиях неопределенности природы
Классические
критерии принятия решения
Слайд 4Принятие решений в условиях неопределенности природы
Результат принятого
решения зависит от некоторых
случайных факторов
А={αj}, j=1,…n,
в общем случае неподвластных ЛПР.
f(x) → max f(x,α).
х
Слайд 5Принятие решений в условиях неопределенности природы
Неопределенность состоит
в том, что каждой альтернативе х ставится в соответствие не
одно значение критерия, а целый набор, определяемый количеством рассматриваемых внешних условий,x → f(x,α)
Как выбрать лучшую альтернативу?
Слайд 6Принятие решений в условиях неопределенности природы
В практических приложениях функция
f(х,α) имеет дискретный характер, т.е. любому допустимому решению хi соответствуют
различные внешние условия αj и результаты решенийf(xi, αj)=fij.
Слайд 9Вектор результатов
Его роль –
поставить в
соответствие каждой альтернативе
одно число
х → fir (x)
Слайд 10Пример
Планирование производственных мощностей
ММ – малые мощности; СМ – средние мощности;
КМ – крупные мощности
Слайд 11Принимать решения, как правило, сравнительно легко. Все сводится к выбору
направления действий.
Трудно принять хорошее решение.
Однако ПР - это
психологический процесс. А человеческое поведение не всегда логично: иногда нами движет логика, иногда - чувства. Поэтому способы, используемые ЛПР для ПР, варьируются от спонтанных до логичных.
При этом ЛПР находится под воздействием таких психологических факторов, как социальные установки, накопленный опыт и личностные ценности.
Слайд 14Вектор результатов fir
fir=max fij
- оптимистическая
j
fir=min fij
- пессимистическаяj
fir=max fij +min fij - компромисса
j j
fir=Σ fij - нейтралитета
j
Слайд 16Классические критерии ПР
Минимаксный критерий, или критерий Вальда
Оценочная функция ММ-критерия:
ZMM=max (min fij)
i jПозиция крайнего пессимизма
Слайд 18Правило выбора (MM)
Матрица решений дополняется еще одним столбцом из
наименьших результатов fir каждой строки.
Выбрать следует те варианты, в
строках которых стоят наибольшие значения fir этого столбца Слайд 19Замечание
Выбранные таким образом варианты полностью исключают риск:
нельзя
столкнуться с результатом, хуже, чем max fir, какие бы условия
αj ни встретилисьСлайд 21Применение ММ-критерия
о возможности появления внешних состояний αj ничего
не известно;
приходится считаться с появлением различных внешних состояний αj;
решение реализуется
один раз;необходимо исключить какой бы то ни было риск
Слайд 26Правило выбора
Любой элемент матрицы решений вычитается из наибольшего результата
соответствующего столбца.
Разности Δij образуют матрицу остатков .
Эта
матрица дополняется столбцом наибольших разностей. Выбирается вариант, где стоит наименьшее для этого столбца значениеСлайд 27Критерий Гурвица (HW)
ZHW=max[c*min fij +(1-c)*max fij]
i j
j0≤c≤1
C=1 – позиция крайнего пессимизма
C=0 – позиция азартного игрока
Позиция взвешенного компромисса
Слайд 28Правило выбора
Матрица решений дополняется столбцом, содержащим
средневзвешенную сумму наименьшего и
наибольшего результатов для любой строки
Выбираются те варианты, где
стоят наибольшие значения fir этого столбцаСлайд 30Применение HW
о вероятностях появления событий αj ничего не известно;
реализуется малое
количество решений;
допускается некоторый риск
Слайд 32Неопределенности природы
В условиях полной неопределенности решение определяется позицией ЛПР и
принимается по одному из критериев:
ММ, S, HWЛПР должен найти устойчивое решение или обосновать свою позицию
Если решение неустойчиво, то необходима дополнительная информация
Слайд 33Классические критерии ПР
Критерий Байеса-Лапласа (BL)
αj → pj - дополнительная
информация, pj=Вер{αj}
n nfir = ∑ fijpj , ZBL=max ( ∑ fijpj)
n j=1 i j=1
Σpj=1
j=1
Слайд 35Правило выбора
Матрица решений дополняется еще одним столбцом, содержащим математические
ожидания результатов каждой строки
Выбираются те варианты хi, в строках
которых стоит наибольшее значение fir этого столбцаСлайд 36Применение BL
вероятности появления состояний αj известны и не зависят от
времени
решение реализуется бесконечно (теоретически) много раз
для малого числа
реализаций решения допускается некоторый рискСлайд 37Позиция ЛПР (BL)
Исходная позиция ЛПР, применяющего критерий BL, оптимистичнее, чем
при минимаксном критерии, однако предполагает более высокий уровень информированности и
достаточно много реализацийСлайд 38Классические критерии ПР
(пример)
Планирование производственных мощностей
ММ – малые мощности; СМ –
средние мощности; КМ – крупные мощности
Слайд 41Критерий Гермейера (G)
Правило выбора: Матрица решений дополняется еще одним
столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней
результата fij на вероятность соответствующего состояния αjВыбираются те варианты, где стоит максимальное значение этого столбца
Слайд 43Планирование эксперимента в условиях неопределенности
Предстоит принять решение в недостаточно выясненных
условиях.
Имеет ли смысл для уточнения условий в данной неопределенной
ситуации предпринять некоторый эксперимент? Слайд 46Эксперимент
Рассмотрим сначала случай “идеального” эксперимента ε, приводящего к совершенно точному
знанию того состояния αj, которое имеет место в данной ситуации
Слайд 47Эксперимент?
||fij||, вероятности Р(αj)=pj
Обозначим затраты на проведение
эксперимента cost
Сравним средний выигрыш без проведения эксперимента ε и средний
выигрыш с проведением этого экспериментаСлайд 51Эксперимент
Но нужно заранее решить, следует проводить эксперимент или
нет. Поэтому средний выигрыш =
Слайд 55Идеальный эксперимент ε
затраты на его проведение
меньше
минимального среднего риска
нужно проводить, если
Слайд 58Эксперимент
В случае, когда эксперимент нецелесообразен,
следует выбрать альтернативу,
оптимальную по BL-критерию
Слайд 62Пример
Некоторый объект надо подвергнуть проверке с приостановкой его
эксплуатации. Из-за этого приостанавливается выпуск продукции. Если же своевременно не
обнаружить неисправность, то это приведет не только к приостановке работы, но и к поломкеСлайд 63Пример
Варианты решения:
Х1 - полная проверка;
Х2 -
минимальная проверка;
Х3 - отказ от проверки.
Слайд 64Пример
Состояния αj:
α1 - неисправностей нет;
α2 - имеется незначительная
неисправность;α3 - имеется серьезная неисправность
Слайд 65Пример
Результаты fij:
затраты на проверки и устранение неисправностей;
затраты, связанные
с потерями в выпуске продукции и с поломкой.
Слайд 67Пример
Является ли целесообразным “идеальный” эксперимент, стоимость которого cost=2?
5,2
4,5
5,0
Слайд 68Неидеальный эксперимент
Рассмотрим неидеальный эксперимент ε,
который не выясняет точно состояния
αj, а дает
какие-то косвенные свидетельства в пользу тех или
иных состояний.Предположим, что эксперимент ε приводит к появлению одного из Bk несовместных событий В1, В2,…, Вk:
причем вероятности событий зависят от условий, в которых они проводятся.
Слайд 69Обозначим условную вероятность события Bl в условиях αj P(Bl/αj) и
будем считать, что она нам известна.
После осуществления эксперимента ε,
давшего исход Bl, состояния природы αj будут характеризоваться не априорными, а новыми, апостериорными вероятностями: - это условные вероятности событий αj, они подсчитываются по известной формуле Байеса
Слайд 70- это условные вероятности событий αj,
подсчитываются по формуле Байеса
при
условии, что эксперимент дал результат Bl.
Слайд 71Рассмотрим предыдущий пример с неидеальным экспериментом, который имеет три возможных
исхода: B1, B2, B3.
В эксперименте имеет место исход B1.
Вычислить апостериорные вероятности и найти оптимальное решение.Слайд 72Решение
Вычислим апостериорные вероятности по формуле Байеса:
P11= P1*P(B1/α1) /
P21=0,392P31=0,435
P41=0,130
Слайд 74Функции управления
Для управленцев различного концептуального статуса существуют свои
функции,
задачи, традиции,
представления о входной и выходной информации
Слайд 75Концептуальный уровень иерархии управления
«Исполнитель»
Исполнение точно поставленных
задач, детальных указаний;
минимум свободы принятия решений (только
в части нюансов технологии исполнения задания) Слайд 76«Администратор»
Руководство группой исполнителей или небольшими отделами организации,
принятие решений
о тактике действий, выбор способа распределения небольших объемов активных ресурсов
Слайд 77«Руководитель звена отрасли»
Руководство крупной организацией, определение подробной тактики действий
и элементов стратегии поведения,
участие в разработке решений по стратегическим
вопросам Слайд 81Источники индивидуального риска
Инициатива (авантюризм, честолюбие, эгоизм, стремление к лидерству)
Статус (исполнение
функций управления, исполнение задач взаимодействия, исполнение обязанностей по должности)
Слайд 82Источники ситуационного риска
Время (дефицит времени на принятие решения, временная отдаленность
будущих последствий)
Ресурсы (недостаток ресурсов, ограниченность резерва)
Информация (об исходах операции, о
ее результатах)Интересы и действия других лиц (один субъект, неорганизованная группа, организованная группа)
Слайд 83ЛПР должно руководить
Обеспечение наименьшего уровня риска требует непрерывного руководства.
Оставаясь длительное
время без руководства, любое дело, как и автомобиль, может двигаться
только в одном направлении – под откос!Слайд 84Понятие рационального выбора.
Основные типы неопределенностей, встречающихся при принятии решений.
Характеристика неопределенностей
природы.
В чем состоит идея преодоления природных неопределенностей?
Роль вектора результатов.
В чем
проявляется субъективизм при принятии решения?Сколько целевых функций может быть в задачах неопределенности природы?
Как направлены целевые функции в задачах неопределенности природы?
Как сравнивать альтернативы в задачах неопределенности природы?
Какая позиция ЛПР не допускает риск?
Что является формой представления задачи неопределенности природы?
Какой смысл имеют числа в матрице решений?
Позиция ЛПР и классические критерии.
Какие критерии выражают пессимистическую позицию ЛПР?
Смысл и роль оценочной функции.
Понятие риска.
Какой знак имеют элементы матрицы остатков?
Какие критерии применяются в условиях полной неопределенности?
Какой критерий применяется в условиях риска, когда известны вероятности внешних условий?
Когда имеет смысл для уточнения условий в данной неопределенной ситуации предпринять некоторый эксперимент?
Как вычислить допустимую стоимость эксперимента?
Как оценить целесообразность эксперимента?
Идеальный эксперимент и неидеальный эксперимент

























![Разработка управленческих решений Критерий Гурвица (HW)ZHW=max[c*min fij +(1-c)*max fij] i Критерий Гурвица (HW)ZHW=max[c*min fij +(1-c)*max fij] i](/img/thumbs/b4c41d21465b9d4d1e0926924e59a50f-800x.jpg)