Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
Содержание
- 1. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ
- 2. РАЗВЕРТКА ПОВЕРХНОСТИ – ЭТО ПЛОСКАЯ
- 3. СВОЙСТВА РАЗВЕРТОК1. КАЖДОЙ ТОЧКЕ ПОВЕРХНОСТИ СООТВЕТСТВУЕТ ТОЧКА
- 4. 4. ДЛИНЫ ДВУХ СООТВЕТСТВУЮЩИХ
- 5. ВИДЫ РАЗВЕРТОКТОЧНЫЕ – ПОСТРОЕННЫЕ ГРАФОАНАЛИТИЧЕСКИМ СПОСОБОМ2. ПРИБЛИЖЕННЫЕ
- 6. СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК ПОВЕРХНОСТЕЙ АППРОКСИМАЦИЯ –
- 7. АППРОКСИМАЦИЯ В КРУГОВОЕ ОСНОВАНИЕ
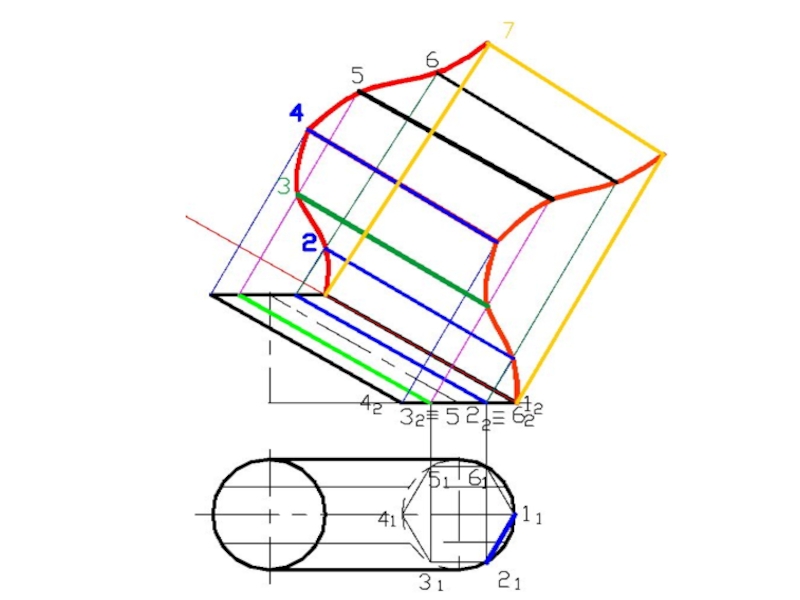
- 8. СПОСОБ НОРМАЛЬНОГО СЕЧЕНИЯ
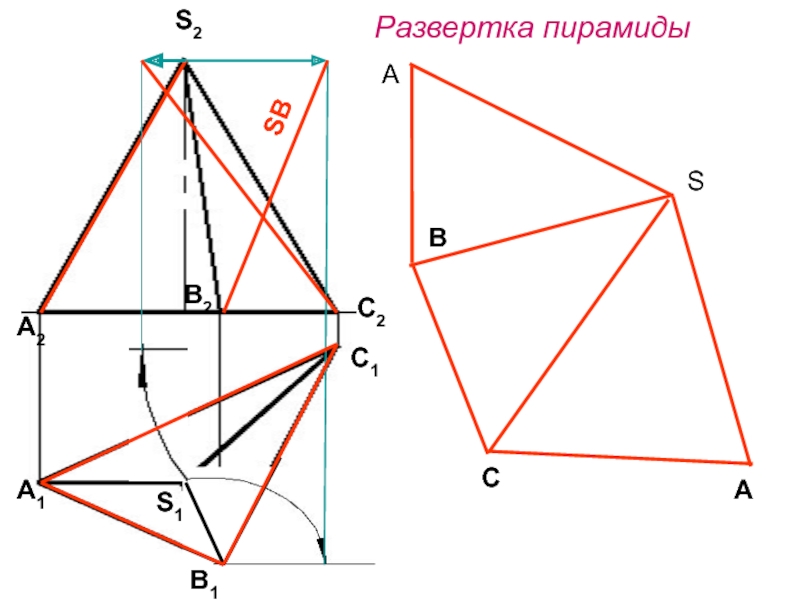
- 9. Развертка пирамидыА1С1А2В2С2S2S1В1SBSAВСА
- 10. Развертка цилиндра прямого кругового Цилиндр: Диаметр 40 мм Высота 50 ммL= 2pR =pDDHH
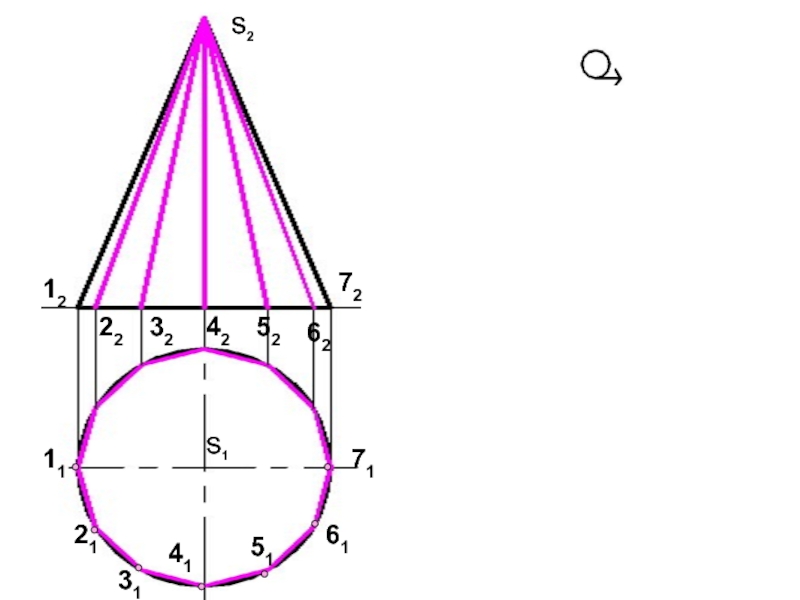
- 11. 11214151617131311411211111611711511
- 12. Развертка конуса прямого кругового Конус: Диаметр 40 мм Высота 60 ммS2S1
- 13. 1121314151617112223242527262s2s1
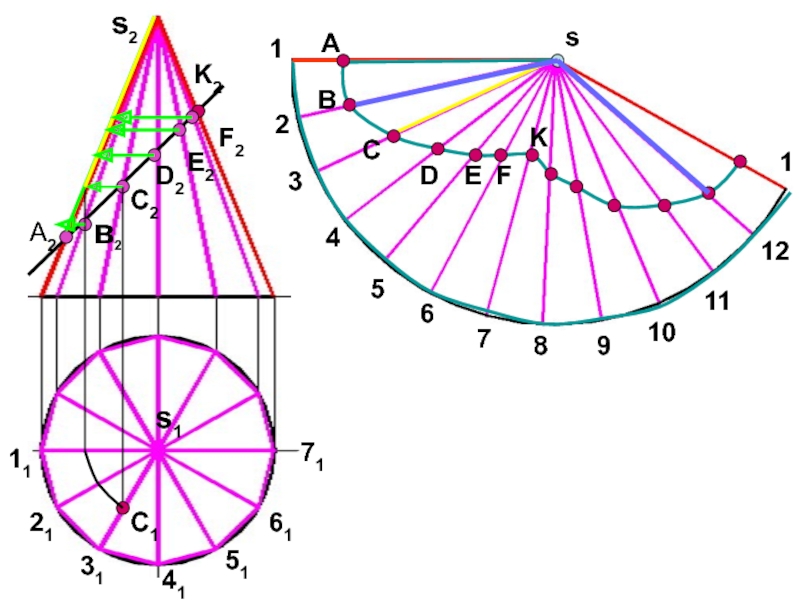
- 14. 112131415161711234567891011121s2s1sА2в2С2D2E2F2K2C1ACBDEFK
- 15. Способ раскатки
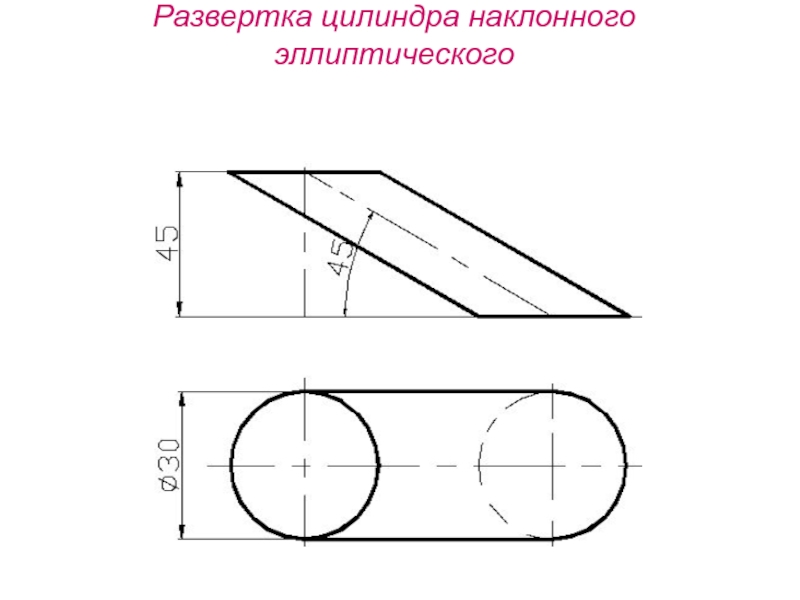
- 16. Развертка цилиндра наклонного эллиптического
- 17. Слайд 17
- 18. Способ триангуляцииКонус с недоступной вершиной
- 19. 11314121122232421243516156411412
- 20. Развертка конуса с не доступной вершиной
- 21. Слайд 21
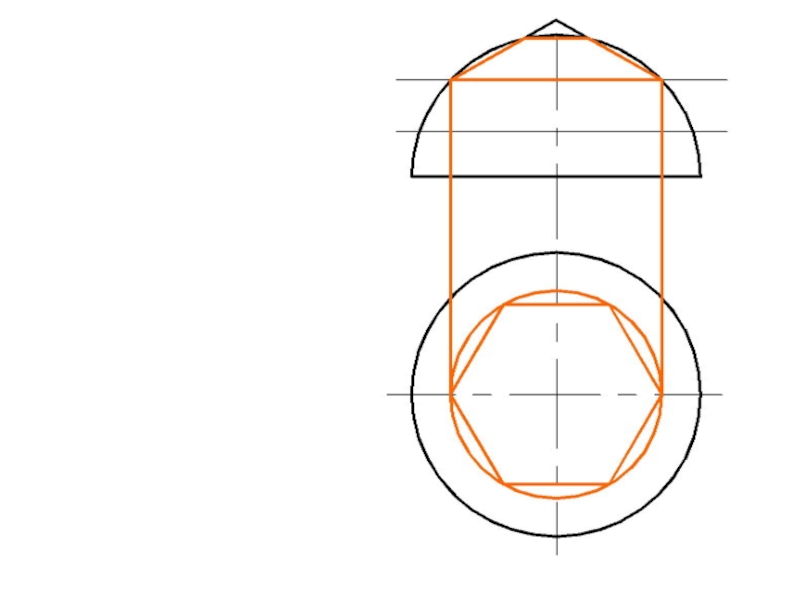
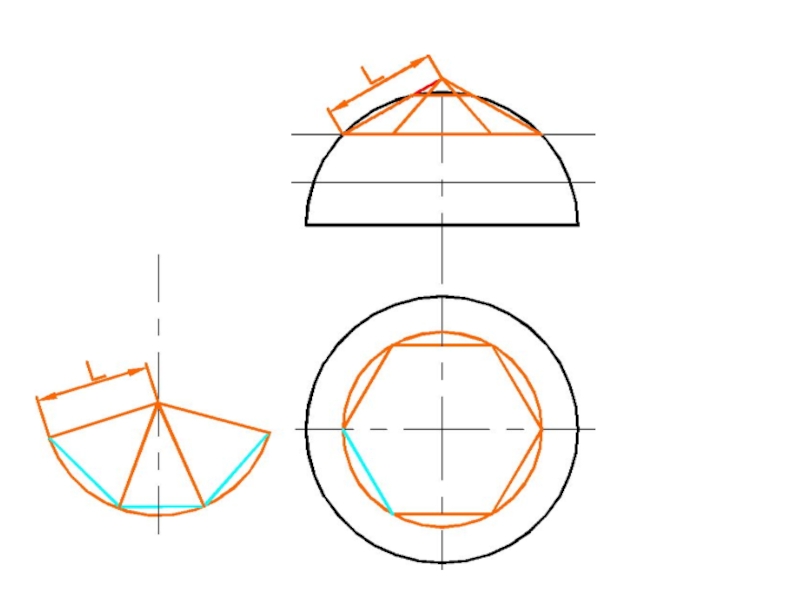
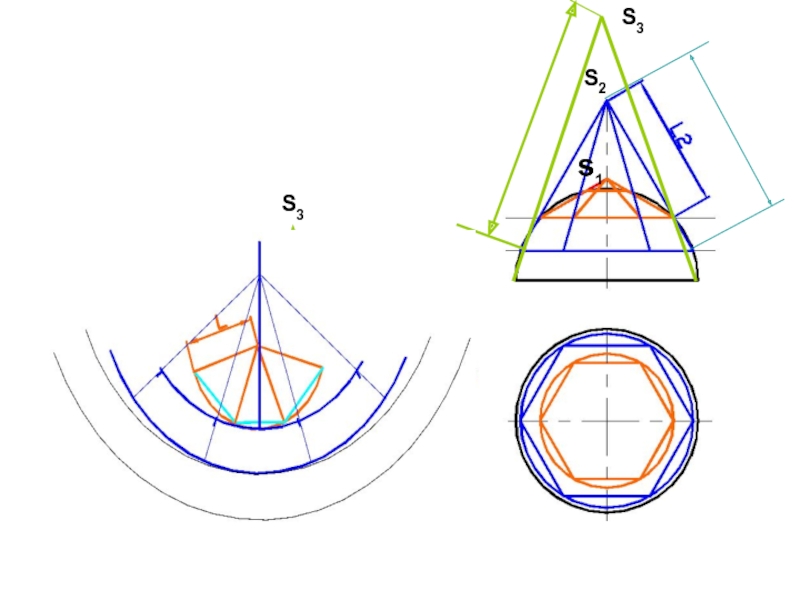
- 22. Развертка сферыИспользуем двойную аппроксимациюРазделим сферу на несколько
- 23. Слайд 23
- 24. Слайд 24
- 25. S2s1s1S2S3S3
- 26. Слайд 26
- 27. Скачать презентанцию
РАЗВЕРТКА ПОВЕРХНОСТИ – ЭТО ПЛОСКАЯ ФИГУРА, КОТОРАЯ ПОЛУЧАЕТСЯ СОВМЕЩЕНИЕМ ВСЕЙ БОКОВОЙ ПОВЕРХНОСТИ ОБЪЕКТА С ПЛОСКОСТЬЮ
Слайды и текст этой презентации
Слайд 3СВОЙСТВА РАЗВЕРТОК
1. КАЖДОЙ ТОЧКЕ ПОВЕРХНОСТИ СООТВЕТСТВУЕТ ТОЧКА НА РАЗВЕРТКЕ
2. ПРЯМОЙ
НА ПОВЕРХНОСТИ СООТВЕТСТВУЕТ ПРЯМАЯ НА РАЗВЕРТКЕ.
(ОБРАТНОЕ УТВЕРЖДЕНИЕ
НЕ ИМЕЕТ МЕСТА)3. ПАРАЛЛЕЛЬНЫМ ПРЯМЫМ НА ПОВЕРХ-
НОСТИ СООТВЕТСТВУЮТ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ НА РАЗВЕРТКЕ
Слайд 44. ДЛИНЫ ДВУХ СООТВЕТСТВУЮЩИХ
ЛИНИЙ
ПОВЕРХНОСТИ И РАЗВЕРТКИ
РАВНЫ МЕЖДУ СОБОЙ
СЛЕДСТВИЕ: ЗАМКНУТАЯ ЛИНИЯ НА ПОВЕРХНОСТИ И СООТВЕТСТВУЮЩАЯ ЕЙ ЛИНИЯ НА РАЗВЕРТКЕ, ОГРАНИЧИВАЮТ ОДИНАКОВУЮ ПЛОЩАДЬ5. УГОЛ МЕЖДУ ЛИНИЯМИ НА ПОВЕРХНОСТИ, РАВЕН УГЛУ МЕЖДУ СООТВЕТСТВУЮЩИМИ ЛИНИЯМИ НА РАЗВЕРТКЕ
Слайд 5ВИДЫ РАЗВЕРТОК
ТОЧНЫЕ – ПОСТРОЕННЫЕ ГРАФОАНАЛИТИЧЕСКИМ СПОСОБОМ
2. ПРИБЛИЖЕННЫЕ – ВЫПОЛНЕННЫЕ СПОСОБОМ
АППРОКСИМАЦИИ РАЗВЕРТКИ РАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ (ЦИЛИНДРЫ, КОНУСЫ)
3. УСЛОВНЫЕ – РАЗВЕРТКИ НЕРАЗВЕРТЫВАЕМЫХ ПОВЕРХНОСТЕЙ
(СФЕРА, ТОР)
Слайд 6СПОСОБЫ ПОСТРОЕНИЯ РАЗВЕРТОК ПОВЕРХНОСТЕЙ
АППРОКСИМАЦИЯ – ЗАМЕНА СЛОЖНОЙ ПОВЕРХНОСТИ
ПРОСТОЙ, ВПИСАННОЙ ИЛИ ОПИСАННОЙ МНОГОГРАННОЙ ПОВЕРХНОСТЬЮ
1. СПОСОБ НОРМАЛЬНОГО
СЕЧЕНИЯ2. СПОСОБ РАСКАТКИ
3. СПОСОБ ТРИАНГУЛЯЦИИ
Слайд 7АППРОКСИМАЦИЯ
В КРУГОВОЕ ОСНОВАНИЕ ВПИСЫВАЮТ ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК,
ЧЕРЕЗ ВЕРШИНЫ МНОГОУГОЛЬНИКА ПРОВОДЯТ РЕБРА ПРИЗМЫ ИЛИ ПИРАМИДЫ
Слайд 22Развертка сферы
Используем двойную аппроксимацию
Разделим сферу на несколько горизонтальных поясов
Каждый пояс
аппроксимируем усеченным конусом
Усеченный конус аппроксимируем вписанной усеченной пирамидой
