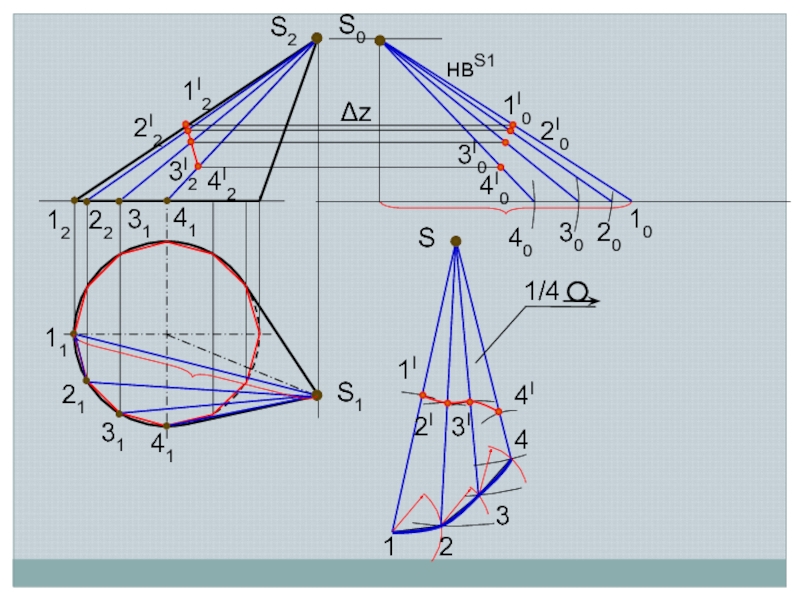
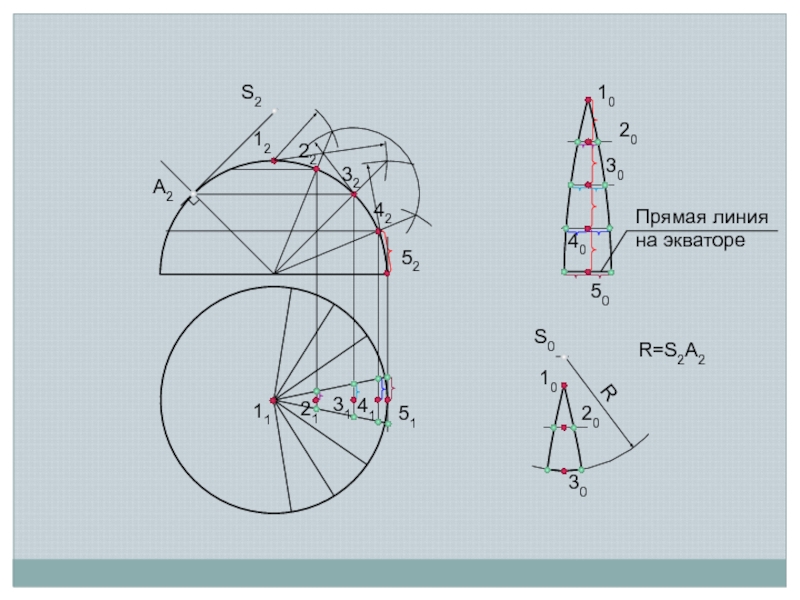
одинаковы
2. Углы между обыкновенными линиями на поверхности равны соответствующим углам
на разверткеУглом между линиями называют угол, образованный их касательными, проведенными в точке пересечения линий
Преобразование, в котором сохраняется равенство углов называется конформным Поэтому поверхность и развертка конформны



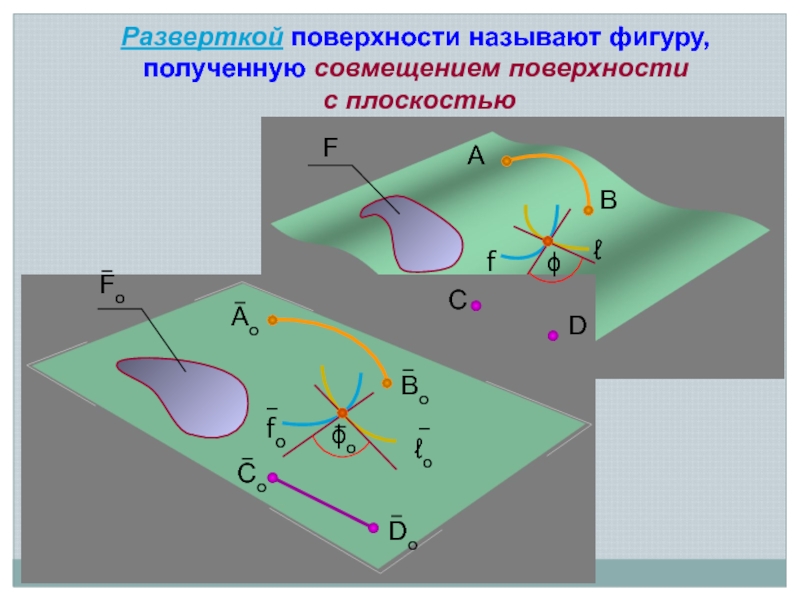





![РАЗВЕРТКИ ПОВЕРХНОСТЕЙ S2A2B2S1ℓ =180 – [град]DℓS0A0B0A0B0Точные разверткиB1A1 S2A2B2S1ℓ =180 – [град]DℓS0A0B0A0B0Точные разверткиB1A1](/img/tmb/3/266209/fe4d25134067f8a1f754c5514af0e625-800x.jpg)