Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реальные газы 1 Уравнение состояния идеального газа – уравнение Менделеева –
Содержание
- 1. Реальные газы 1 Уравнение состояния идеального газа – уравнение Менделеева –
- 2. Слайд 2
- 3. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами
- 4. С учетом этих соображений уравнение состояния идеального
- 5. Силы Ван-дер-Ваальса Я.Д. Ван-дер-Ваальс предположил, что на
- 6. Межмолекулярные силы взаимодействия имеют электрическую
- 7. Слайд 7
- 8. Отметим, что все три силы и энергии
- 9. Силы отталкивания действуют между молекулами на очень
- 10. Полагаем, что U(r = ) = 0
- 11. Уравнение Ван-дер-Ваальса учитывает конечные размеры
- 12. Для = m/ молей газа уравнение
- 13. В объеме газа действие сил притяжения между
- 14. Дополнительное внутреннее давление пропорционально числу частиц, приходящихся
- 15. Избыточное внутреннее давление Pi
- 16. Учитывая совместное действие сил притяжения и сил
- 17. Слайд 17
- 18. Проанализируем изотермы уравнения Ван-дер-Ваальса – зависимости Р
- 19. Поскольку данное уравнение имеет третью
- 20. T1< Tкр
- 21. Изотерма при Ткр разделяет немонотонные
- 22. При температуре газа ниже критической
- 23. Наличие критической точки на изотерме Ван-дер-Ваальса означает,
- 24. Такую температуру Менделеев назвал температурой абсолютного кипения.
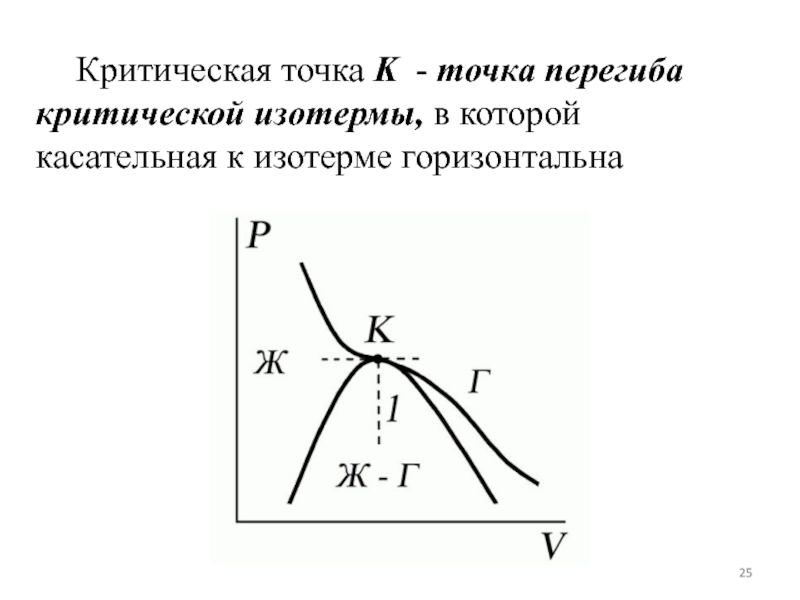
- 25. Критическая точка K - точка перегиба критической изотермы, в которой касательная к изотерме горизонтальна
- 26. Энергия одного моля газа Ван-дер-Ваальса
- 27. Потенциальная энергия притяжения молекул равна работе, необходимой
- 28. Полная энергия одного моля газа Ван-дер-Ваальса : Если
- 29. Основные результаты Уравнение Ван-дер-Ваальса для произвольного
- 30. Слайд 30
- 31. Слайд 31
- 32. Контрольные вопросыПеречислите условия отклонения поведения газов от
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации.
Слайд 3 Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса)обратно пропорциональны
шестой степени расстояния между ними, или второй степени объема, занимаемого
газом. Силы притяжения суммируются с внешним давлением.Уравнение Ван-дер-Ваальса (1873).
Слайд 4 С учетом этих соображений уравнение состояния идеального газа преобразуется в
уравнение Ван-дер-Ваальса:
или для одного моляСлайд 5Силы Ван-дер-Ваальса
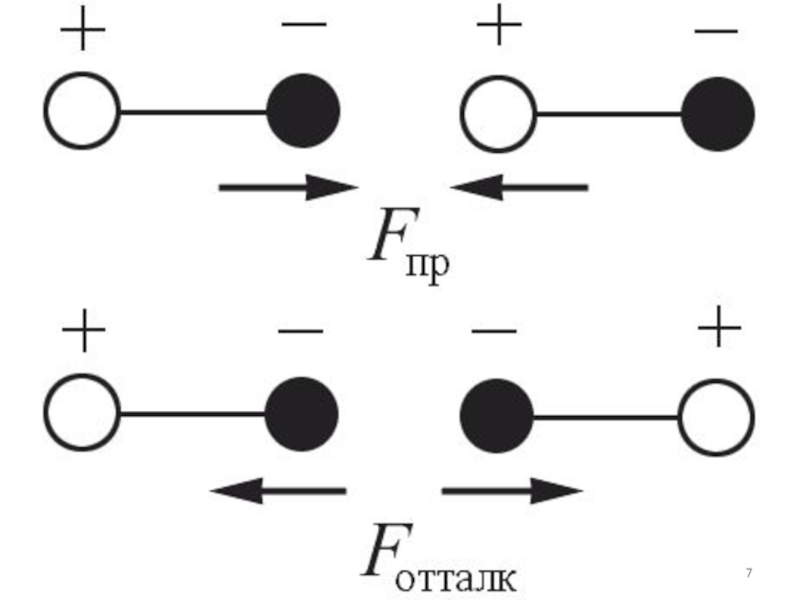
Я.Д. Ван-дер-Ваальс предположил, что на малых расстояниях между
молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами
притяжения.Слайд 6 Межмолекулярные силы взаимодействия имеют электрическую природу и складываются
из:
сил притяжения (ориентационных, индукционных, дисперсионных)
и сил отталкивания.
Слайд 8 Отметим, что все три силы и энергии одинаковым образом убывают
с расстоянием: F = Fор + Fинд
+ Fдисп ~ r –7 U = Uор + Uинд + Uдисп ~ r –6Слайд 9 Силы отталкивания действуют между молекулами на очень малых расстояниях, когда
происходит взаимодействие электронных оболочек атомов, входящих в состав молекул.
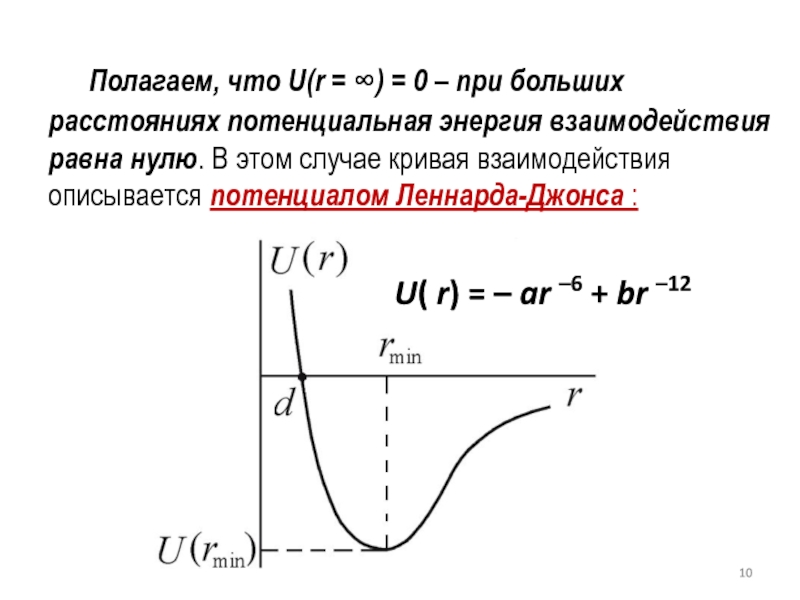
Потенциальная энергия сил отталкивания возрастает с уменьшением расстояния по закону Uот(r) ~ r –12, а, соответственно, сила отталкивания растет как Fот ~ r –13.Слайд 10 Полагаем, что U(r = ) = 0 – при больших
расстояниях потенциальная энергия взаимодействия равна нулю. В этом случае кривая
взаимодействия описывается потенциалом Леннарда-Джонса :U( r) = – ar –6 + br –12
Слайд 11 Уравнение Ван-дер-Ваальса учитывает конечные размеры всех молекул, что
становится существенным при больших давлениях, а также притяжение
молекул в результате межмолекулярного взаимодействия.Вывод уравнения Ван-дер-Ваальса
Слайд 12 Для = m/ молей газа уравнение состояния газа с
учетом конечного размера молекул примет вид: P(V b) = RT. Уравнение
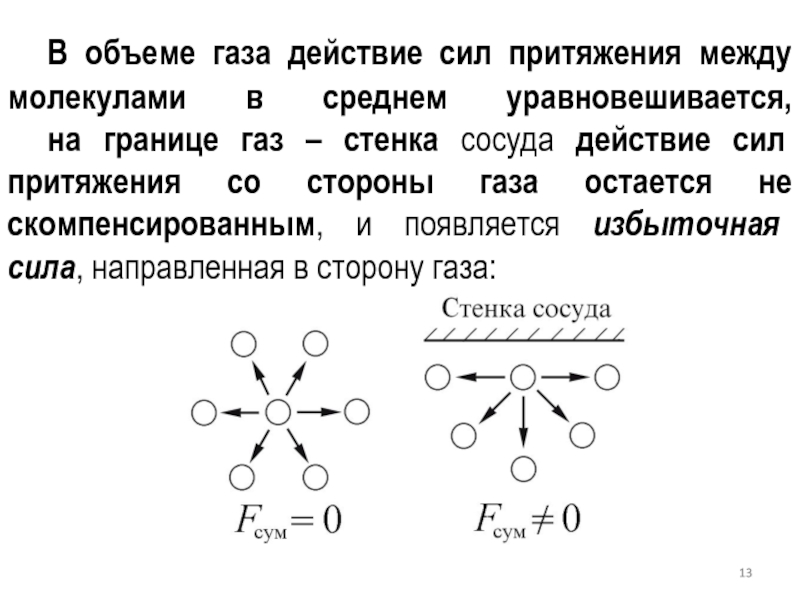
является приближенным и выведено в предположении только парных столкновений.Слайд 13 В объеме газа действие сил притяжения между молекулами в среднем
уравновешивается, на границе газ – стенка сосуда действие сил притяжения
со стороны газа остается не скомпенсированным, и появляется избыточная сила, направленная в сторону газа:Слайд 14 Дополнительное внутреннее давление пропорционально числу частиц, приходящихся на единицу площади
границы nS и силе взаимодействия этих частиц с другими частицами
газа, находящимися в единице объема nV.Слайд 15 Избыточное внутреннее давление Pi если в сосуде
находится один моль газа
Pi = a/V 2, где а – постоянная величина, своя для каждого сорта газа. В случае -молей имеем Pi = 2a/V 2.Слайд 16 Учитывая совместное действие сил притяжения и сил отталкивания и полученные
поправки для объема и давления в уравнении Менделеева-Клапейрона, получим уравнение
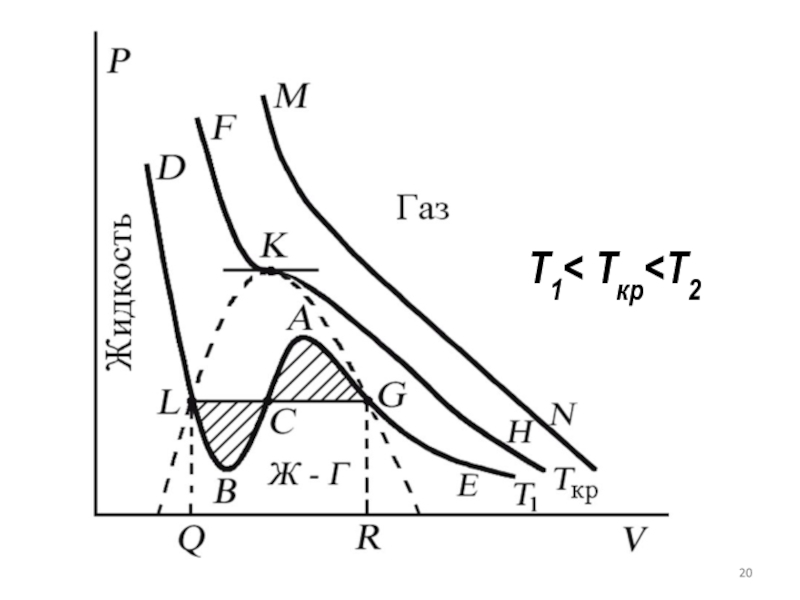
Ван-дер-Ваальса для реального газаСлайд 18 Проанализируем изотермы уравнения Ван-дер-Ваальса – зависимости Р от V для
реального газа при постоянной температуре. (P + 2 a/V 2)(V
b) = RT.Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получим:
PV 3 – (RT + bP) V 2 + a2V ab3= 0
Изотермы уравнения Ван-дер-Ваальса
Слайд 19 Поскольку данное уравнение имеет третью степень относительно V,
а коэффициенты при V действительны, то оно имеет либо один,
либо три вещественных корня. Изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках.Слайд 21 Изотерма при Ткр разделяет немонотонные T < Tкр
и монотонные T > Tкр изотермы. При T > Tкр
вещество находится только в одном – газообразном состоянии, как это имело место у идеального газа.Слайд 22 При температуре газа ниже критической есть возможность перехода
вещества из газообразного в жидкое и наоборот.
Слайд 23 Наличие критической точки на изотерме Ван-дер-Ваальса означает, что для каждой
жидкости существует такая температура, выше которой вещество может существовать только
в газообразном состоянии.Слайд 24 Такую температуру Менделеев назвал температурой абсолютного кипения. Выше этой температуры,
согласно Менделееву, газ не может быть сконденсирован в жидкость никаким
увеличением давления.Слайд 25 Критическая точка K - точка перегиба критической изотермы,
в которой касательная к изотерме горизонтальна
Слайд 26 Энергия одного моля газа Ван-дер-Ваальса слагается из:
внутренней
энергии молекул газа;
кинетической энергии теплового
движения центра масс молекул
потенциальной
энергии взаимногопритяжения молекул
Внутренняя энергия газа Ван-дер-Ваальса
Слайд 27 Потенциальная энергия притяжения молекул равна работе, необходимой для разведения молекул
на бесконечное расстояние друг от друга. В этом конечном состоянии
молекулы не взаимодействуют друг с другом, а потенциальную энергию можно считать равной нулю.Слайд 28 Полная энергия одного моля газа Ван-дер-Ваальса :
Если СV не зависит
от температуры, то полная энергия одного моля
Um = CV Т– a/VmСлайд 29Основные результаты
Уравнение Ван-дер-Ваальса для произвольного количества вещества
реального газа учитывает конечный объем молекул b и их взаимодействие
между собой 2a/V2:
где а и b – постоянные Ван-дер-Ваальса
V – объем, занимаемый газом;
P – давление газа на стенки сосуда.
Слайд 32Контрольные вопросы
Перечислите условия отклонения поведения газов от идеального
Определите, что означают
поправки а и b в уравнении Ван-дер-Ваальса
Назовите силы Ван-дер-Ваальса
Нарисуйте график
потенциала Леннарда-Джонса и поясните егоНарисуйте изотермы Ван-дер-Ваальса
Определите, что означает критическая температура