Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реконструкция архитектурных перспектив и приемы фотомонтажа в перспективе
Содержание
- 1. Реконструкция архитектурных перспектив и приемы фотомонтажа в перспективе
- 2. Основные положенияПерспективу строят по ортогональным проекциям объекта,
- 3. В архитектурной практике возникает ряд задач, когда
- 4. Определение по перспективному изображению или фотоснимку размеров,
- 5. КАВSР●●1 случай: отрезок АВрасположен параллельно картинеРассмотрим различные
- 6. КАВSР●●Проведем через точки А и В прямые
- 7. КАВSР●●Если проведем через точки А и В
- 8. Точки измерения .Определение:Точками измерения называются точки
- 9. Рассмотрим второй случай, когда отрезок прямой АВ
- 10. КSР●●3 случай: прямая находится в предметной плоскости
- 11. КSР●●Построим точку схода для прямой АВ. Для
- 12. КSР●●R=CA и R=CB перенесем в картину прямую
- 13. КSР●●Проведем прямые АоА и ВоВ и затем
- 14. КSР●● SF=FF* - то есть расстояние фокуса
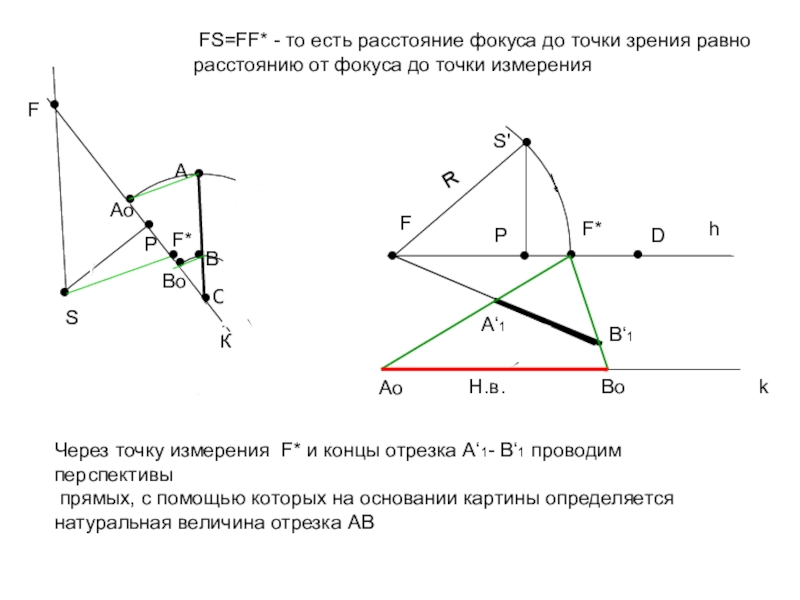
- 15. КSР●● FS=FF* - то есть расстояние фокуса
- 16. КSР●● FS=FF* - то есть расстояние фокуса
- 17. hk●P●DA‘1B‘1●F●S'R●F●*АоВоН.в.●АВПредположим, что нам дана перспектива прямой
- 18. hk●P●DA‘1B‘1●F●S'R●F*АоВоН.в.●АВЧерез точку измерения F* и точки
- 19. Пример построения реконструкции объекта по фотографииПредположим, что
- 20. Пример построения реконструкции объекта по фотографииАЕ●●khF1F2Через (.)А
- 21. Делим расстояние между фокусами пополам и проводим
- 22. Определяем точку Р (обычно это центр
- 23. Из точек F1 и F2 проводим прямые
- 24. Из точки А проводим линию связи и определяем положение точки А на линии нижнего основания картины.G●B●F1●F2●K1K2●AL1L2
- 25. Затем через полученную точку А проводим
- 26. Из точки L2 проводим прямую, параллельную
- 27. Из точки L2 проводим прямую, параллельную
- 28. Следующими действиями мы восстанавливаем план данного объекта.
- 29. Определяем толщину стены с помощью простенков, видимых
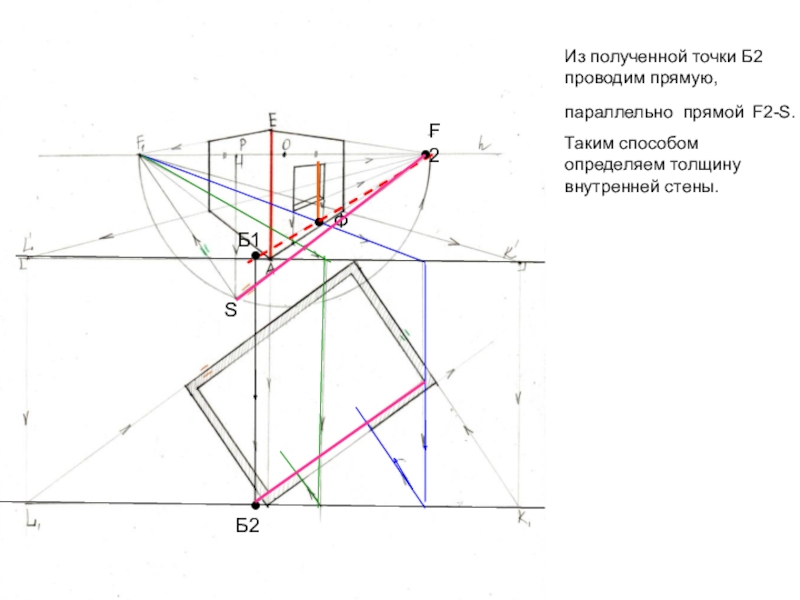
- 30. Из полученной точки Б2 проводим прямую, параллельно прямой F2-S. Таким способом определяем толщину внутренней стены.●F2●●●Б1Б2ФS
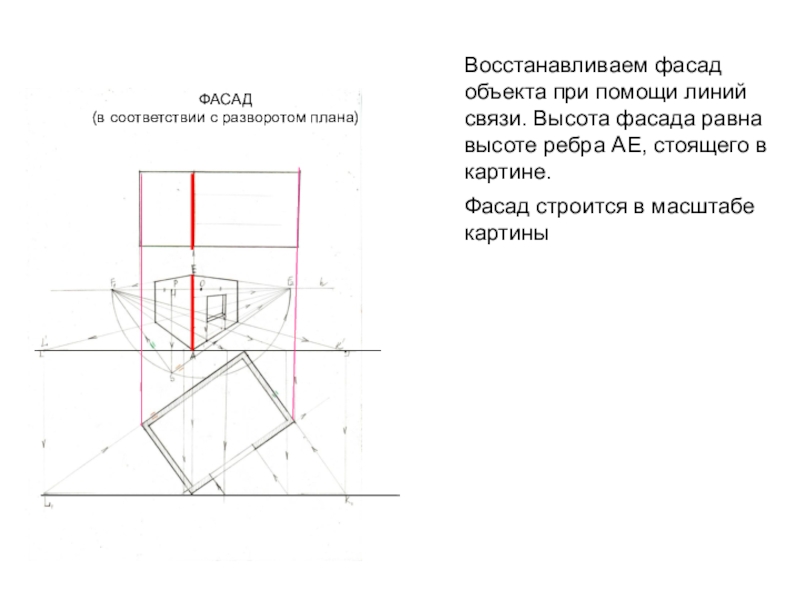
- 31. Восстанавливаем фасад объекта при помощи линий связи.
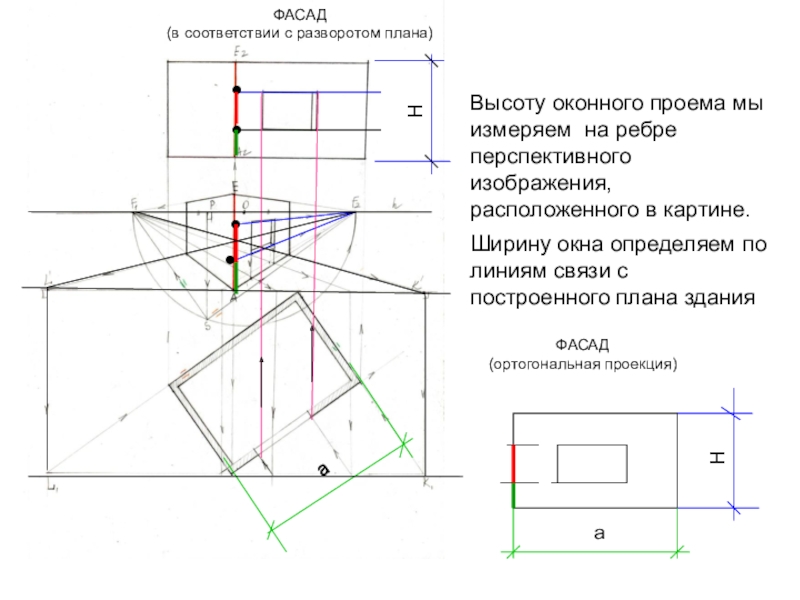
- 32. Высоту оконного проема мы измеряем на ребре
- 33. .Пример реконструкции перспективы●РS●F1●F2●K1K2h
- 34. Затем вычерчивают план и фасад здания в
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Основные положения
Перспективу строят по ортогональным проекциям объекта, по его плану,
фасаду, разрезам, выполненным в определенном масштабе.
(ортогональным) проекциям и не может быть распространено на центральную проекцию, на перспективу. Величина проекции какого-либо элемента объекта в перспективе зависит от того, на каком расстоянии он находится от картинной плоскости и от точки зрения. Таким образом, перспективное изображение объекта на плоскости не определяет метрически точно ни размеров, ни истинной формы, ни положения объекта относительно точки зрения.Слайд 3В архитектурной практике возникает ряд задач, когда по перспективному изображению
или фотоснимку объекта необходимо определить его действительные параметры:
При разработке композиции
объекта и проверке её восприятия с помощью эскизного перспективного изображения с последующей корректировкой композиции на перспективе с внесением соответствующих поправок в ортогональные проекции;При восстановлении, реставрации и реконструкции разрушенных памятников архитектуры, когда необходимо воспроизвести ортогональные чертежи объекта по сохранившемуся фотоснимку;
При необходимости выполнения в короткие сроки и без специальных работ обмерных чертежей по фотоснимкам архитектурного сооружения
Слайд 4Определение по перспективному изображению или фотоснимку размеров, формы и относительного
положения объекта и воспроизведение его ортогональных проекций (плана и фасада)
называется реконструкцией перспективы в ортогонально-проекционный чертежСлайд 5К
А
В
S
Р
●
●
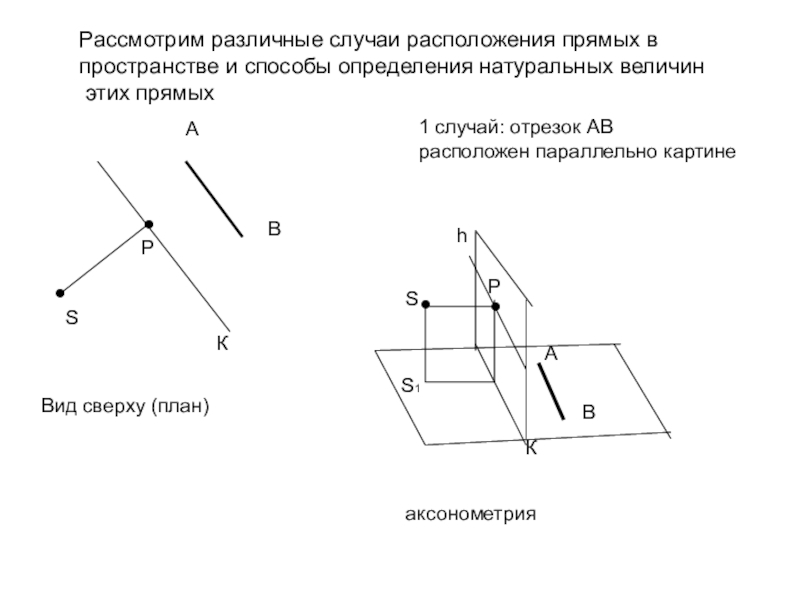
1 случай: отрезок АВ
расположен параллельно картине
Рассмотрим различные случаи расположения прямых
в
пространстве и способы определения натуральных величин
этих прямых
К
А
В
S
S1
P
h
●
●
Вид сверху (план)
аксонометрия
Слайд 6К
А
В
S
Р
●
●
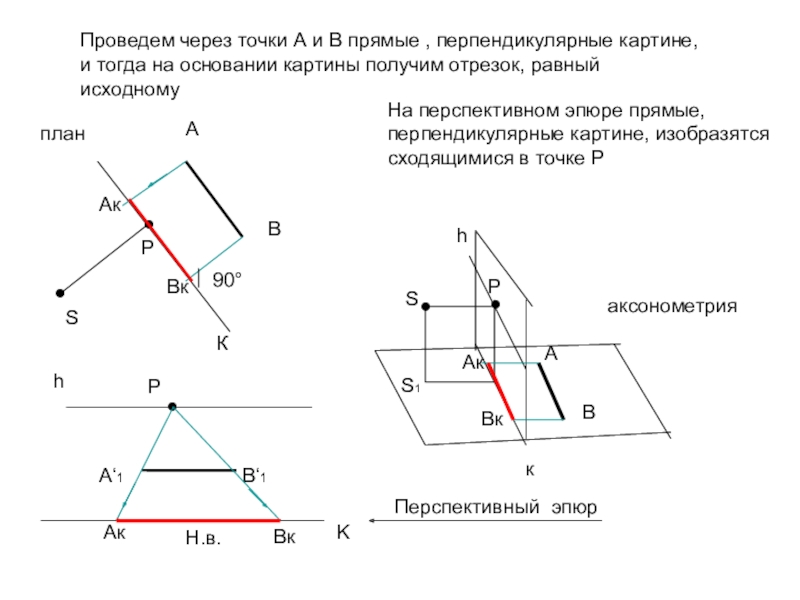
Проведем через точки А и В прямые , перпендикулярные картине,
и тогда на основании картины получим отрезок, равный исходному
к
А
В
S
S1
P
h
90°
●
●
Ак
Вк
Ак
Вк
h
K
●
P
A‘1
B‘1
Ак
Вк
Н.в.
Перспективный эпюр
аксонометрия
план
На перспективном эпюре прямые,
перпендикулярные картине, изобразятся
сходящимися в точке Р
Слайд 7К
А
В
S
Р
●
●
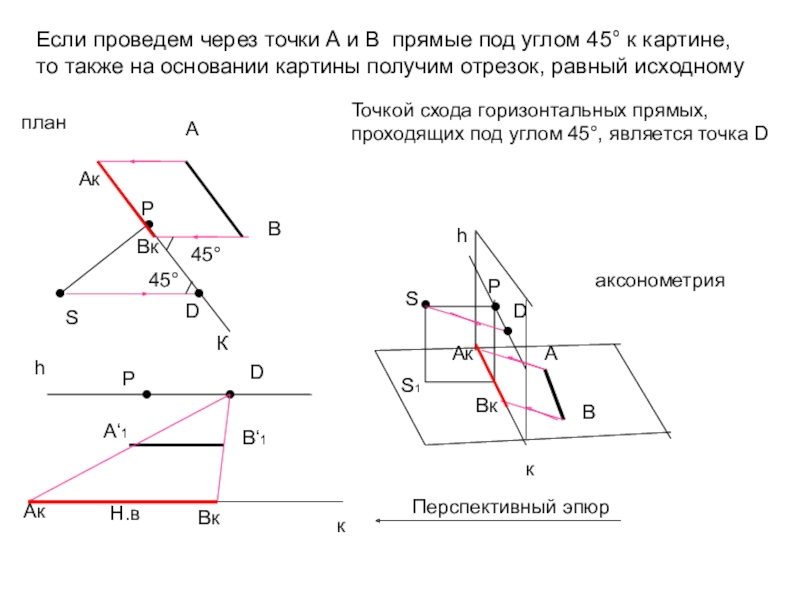
Если проведем через точки А и В прямые под углом
45° к картине,
то также на основании картины получим отрезок, равный
исходномук
А
В
S
S1
P
h
●
●
45°
●
D
Aк
Вк
●
D
h
к
●
●
Р
D
Ак
Вк
Н.в
А‘1
В‘1
Ак
Вк
Точкой схода горизонтальных прямых,
проходящих под углом 45°, является точка D
45°
план
аксонометрия
Перспективный эпюр
Слайд 8Точки измерения
.
Определение:
Точками измерения называются точки на картине, при помощи которых
определяется истинная величина отрезков, заданных в перспективе.
Вывод к 1 случаю:
Любая
точка линии h-h может быть принята за точку измерения, если отрезок II К, или перпендикулярен П.
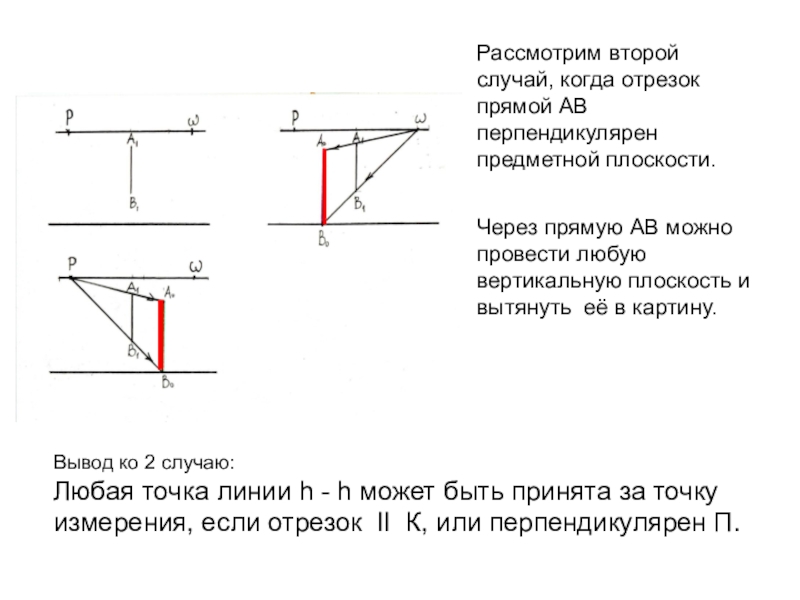
Слайд 9Рассмотрим второй случай, когда отрезок прямой АВ перпендикулярен предметной плоскости.
Через
прямую АВ можно провести любую вертикальную плоскость и вытянуть её
в картину.Вывод ко 2 случаю:
Любая точка линии h - h может быть принята за точку измерения, если отрезок II К, или перпендикулярен П.
Слайд 10К
S
Р
●
●
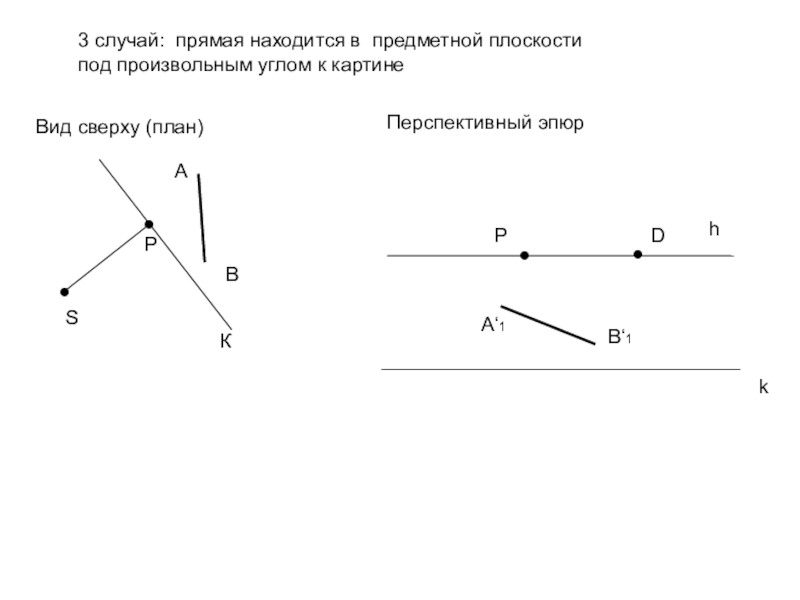
3 случай: прямая находится в предметной плоскости
под произвольным углом к
картине
А
Вид сверху (план)
Перспективный эпюр
h
k
●
P
●
D
В
A‘1
B‘1
Слайд 11К
S
Р
●
●
Построим точку схода для прямой АВ. Для этого через глаза
наблюдателя точку S проведем прямую, параллельную АВ до пересечения с
картиной –получим точку F. Т.к. АВ лежит на полу, точка схода будет лежать на линии горизонта
А
Перспективный эпюр
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Чтобы построить точку измерения для прямой АВ , расположенной
в предметной плоскости, необходимо продлить прямую до пересечения
с картиной –получим точку С
Вид сверху (план)
●
F
●
F
Слайд 12К
S
Р
●
●
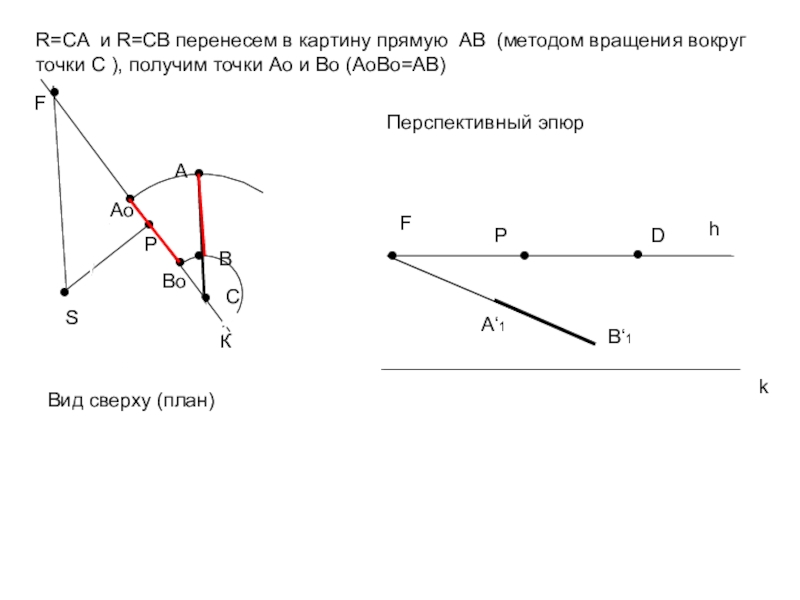
R=CA и R=CB перенесем в картину прямую АВ (методом вращения
вокруг точки С ), получим точки Ао и Во (АоВо=АВ)
А
Перспективный эпюр
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Ао
Во
●
●
●
F
Вид сверху (план)
●
F
Слайд 13К
S
Р
●
●
Проведем прямые АоА и ВоВ и затем найдем точку схода
для этих прямых F*. Рассмотрим полученные треугольники: ΔSFF* подобен ΔСААо,
так как у них одна сторона общая, а две другие параллельны друг другу →СА=САо , SF=FF*
А
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Ао
Во
●
●
●
F
●
F*
Вид сверху (план)
●
F
Перспективный эпюр
Вывод: Точка F*-точка измерения для определения натуральной
величины данной прямой
Слайд 14К
S
Р
●
●
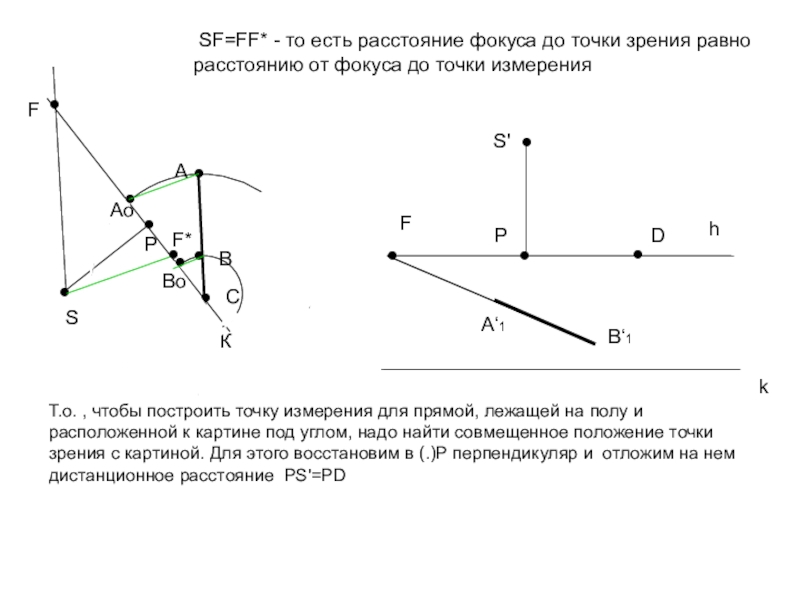
SF=FF* - то есть расстояние фокуса до точки зрения
равно расстоянию от фокуса до точки измерения
А
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Ао
Во
●
●
●
F
●
F*
●
F
Т.о. , чтобы
построить точку измерения для прямой, лежащей на полу и расположенной к картине под углом, надо найти совмещенное положение точки зрения с картиной. Для этого восстановим в (.)Р перпендикуляр и отложим на нем дистанционное расстояние PS'=PD
●
S'
Слайд 15К
S
Р
●
●
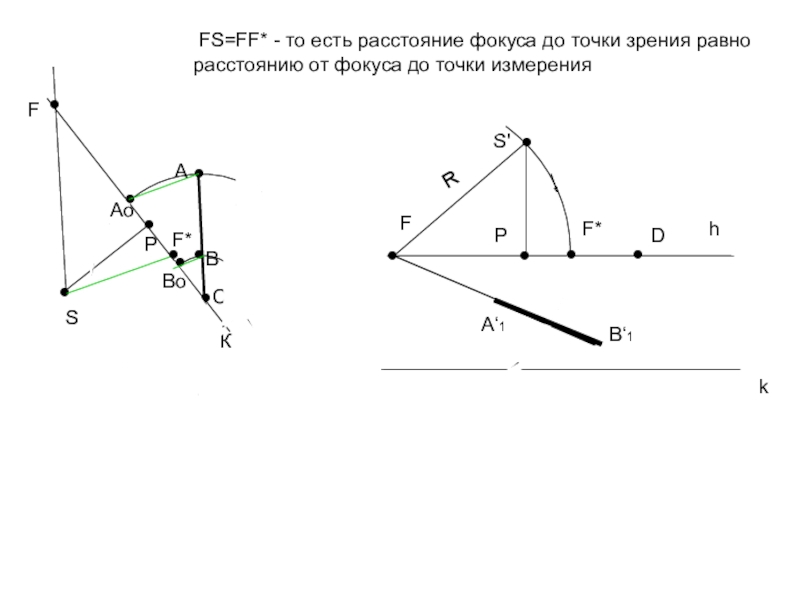
FS=FF* - то есть расстояние фокуса до точки зрения
равно расстоянию от фокуса до точки измерения
А
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Ао
Во
●
●
●
F
●
F*
●
F
●
S'
R
●
F*
Слайд 16К
S
Р
●
●
FS=FF* - то есть расстояние фокуса до точки зрения
равно расстоянию от фокуса до точки измерения
А
h
k
●
P
●
D
В
A‘1
B‘1
●
●
●
С
Ао
Во
●
●
●
F
●
F*
●
F
●
S'
R
●
F*
Ао
Во
Через точку измерения
F* и концы отрезка A‘1- B‘1 проводим перспективыпрямых, с помощью которых на основании картины определяется
натуральная величина отрезка АВ
Н.в.
Слайд 17
h
k
●
P
●
D
A‘1
B‘1
●
F
●
S'
R
●
F●
*
Ао
Во
Н.в.
●
А
В
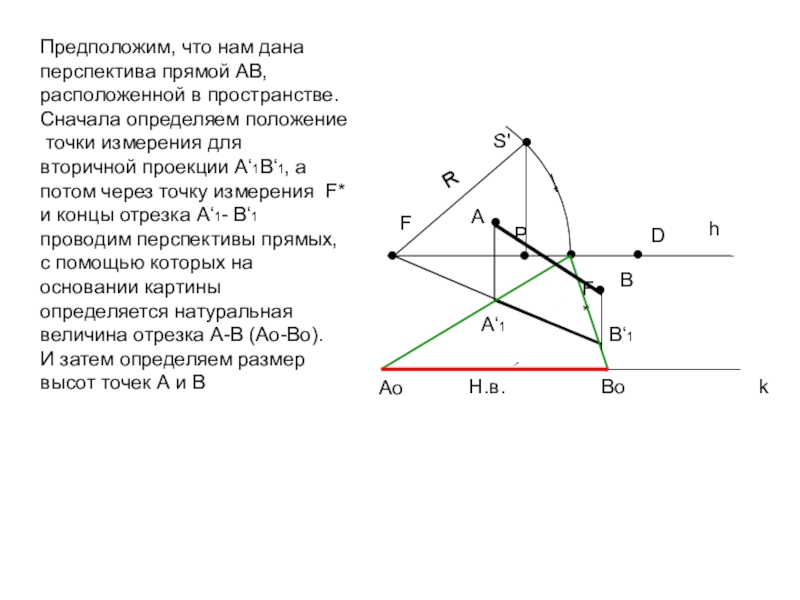
Предположим, что нам дана
перспектива прямой АВ, расположенной в
пространстве.
Сначала определяем положение
точки измерения для
вторичной проекции A‘1B‘1,
а потом через точку измерения F* и концы отрезка A‘1- B‘1 проводим перспективы прямых, с помощью которых на основании картины определяется натуральная величина отрезка А-В (Ао-Во).И затем определяем размер высот точек А и В
Слайд 18
h
k
●
P
●
D
A‘1
B‘1
●
F
●
S'
R
●
F*
Ао
Во
Н.в.
●
А
В
Через точку измерения F* и точки A‘- B‘ проводим
перспективы прямых, и ищем точки их пересечения с линиями связи,
восстановленными в точках Ао и Во.И определяем размер высот точек А и В
●
А
●
В
Слайд 19Пример построения реконструкции объекта по фотографии
Предположим, что у нас есть
Фотография некоторого объекта.
Мы можем предположить, что
переднее ребро стоит
в картине и его величина не будет
деформироваться и изображена в
натуральную величину в масштабе
картины
Слайд 20Пример построения реконструкции объекта по фотографии
А
Е
●
●
k
h
F1
F2
Через (.)А проведем прямую ОХ
и примем ее за основание картины. Продлим стороны фасадов и
определим точки схода F1 и F2 и положение линии горизонта.Слайд 21Делим расстояние между фокусами пополам и проводим окружность радиусом, равным
половине между фокусного расстояния .
R=F1F2/ 2
h
k
●
F2
A
F1
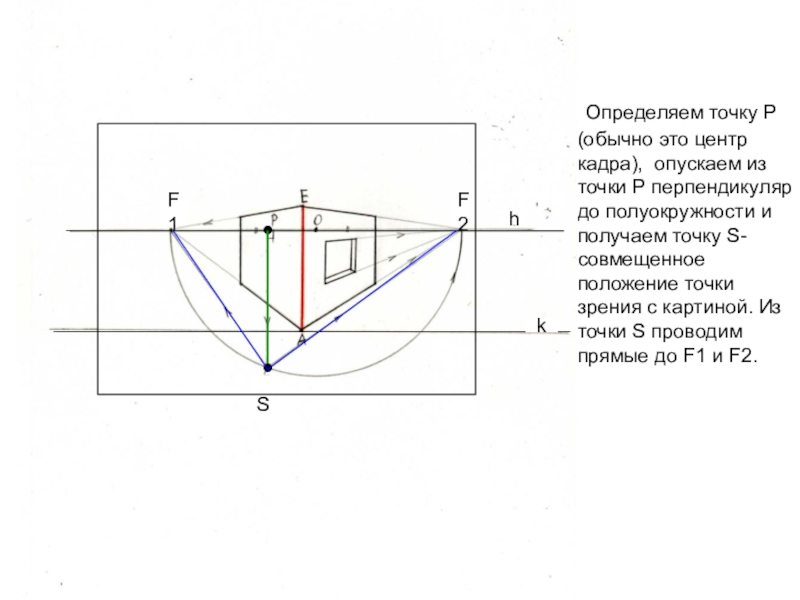
Слайд 22 Определяем точку Р (обычно это центр кадра), опускаем из
точки Р перпендикуляр до полуокружности и получаем точку S- совмещенное
положение точки зрения с картиной. Из точки S проводим прямые до F1 и F2.●
●
S
h
k
F1
F2
Слайд 23Из точек F1 и F2 проводим прямые через точку G
и B до картинной плоскости и опускаем вниз вертикальные прямые
(линии связи) на произвольное расстояние. Ниже фиксируем второе основание картиныG
●
B
●
F1
●
F2
●
K1
K2
●
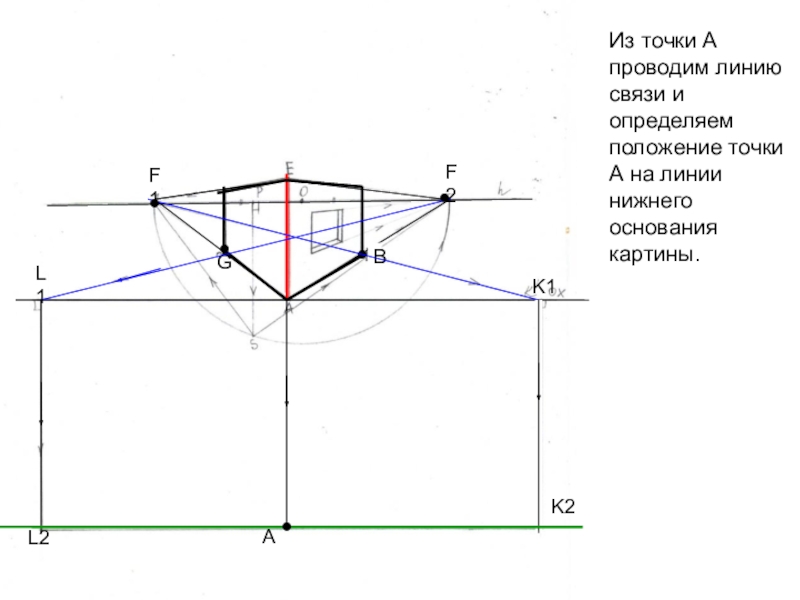
Слайд 24Из точки А проводим линию связи и определяем положение точки
А на линии нижнего основания картины.
G
●
B
●
F1
●
F2
●
K1
K2
●
A
L1
L2
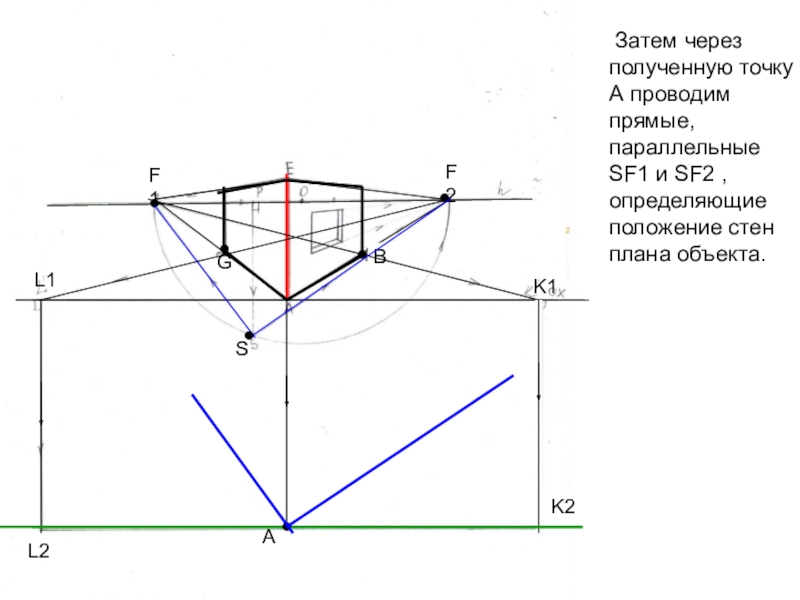
Слайд 25 Затем через полученную точку А проводим прямые, параллельные SF1
и SF2 , определяющие положение стен плана объекта.
G
●
B
●
F1
●
F2
●
K1
K2
●
A
●
S
L1
L2
Слайд 26 Из точки L2 проводим прямую, параллельную SF2 ;из точки
K2 проводим прямую, параллельную SF1 и достраиваем план по полученным
точкам.G
●
B
●
F1
●
F2
●
K1
K2
●
A
●
S
L1
L2
●
●
h
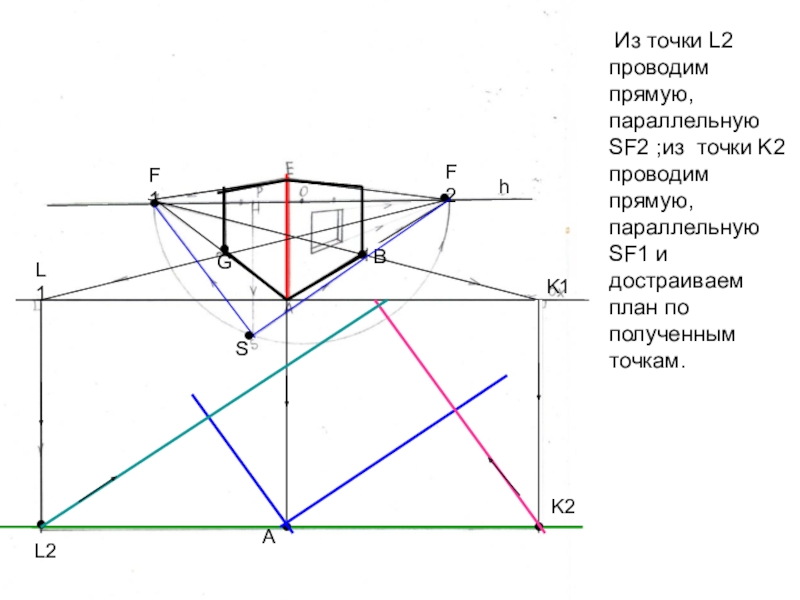
Слайд 27 Из точки L2 проводим прямую, параллельную SF2 ;из точки
K2 проводим прямую, параллельную SF1 и достраиваем план по полученным
точкам.G
●
B
●
F1
●
F2
●
K1
K2
●
A
●
S
L1
L2
●
●
h
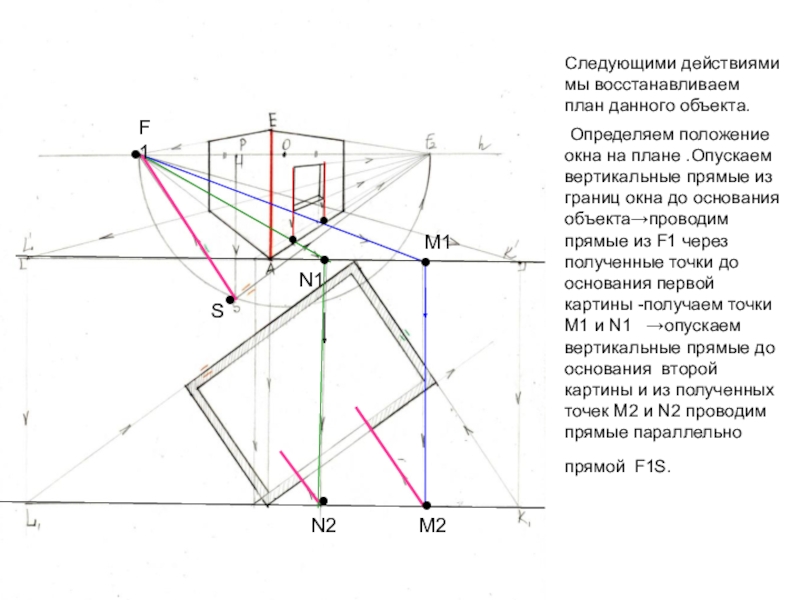
Слайд 28Следующими действиями мы восстанавливаем план данного объекта.
Определяем положение окна
на плане .Опускаем вертикальные прямые из границ окна до основания
объекта→проводим прямые из F1 через полученные точки до основания первой картины -получаем точки M1 и N1 →опускаем вертикальные прямые до основания второй картины и из полученных точек М2 и N2 проводим прямые параллельно прямой F1S.●
●
●
F1
●
S
●
●
●
●
M1
N1
M2
N2
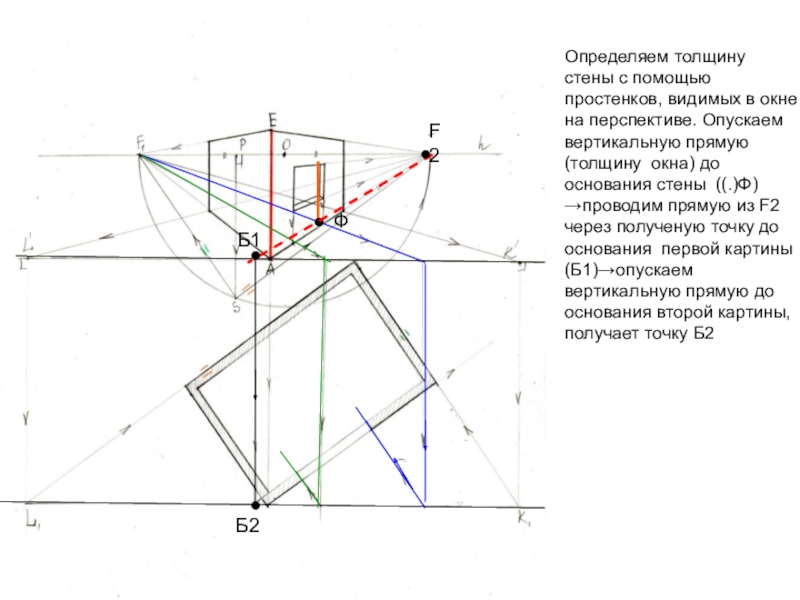
Слайд 29Определяем толщину стены с помощью простенков, видимых в окне на
перспективе. Опускаем вертикальную прямую (толщину окна) до основания стены ((.)Ф)
→проводим прямую из F2 через полученyю точку до основания первой картины (Б1)→опускаем вертикальную прямую до основания второй картины, получает точку Б2●
F2
●
●
●
Б1
Б2
Ф
Слайд 30Из полученной точки Б2 проводим прямую, параллельно прямой F2-S.
Таким
способом определяем толщину внутренней стены.
●
F2
●
●
●
Б1
Б2
Ф
S
Слайд 31Восстанавливаем фасад объекта при помощи линий связи. Высота фасада равна
высоте ребра АЕ, стоящего в картине.
Фасад строится в масштабе картины
ФАСАД
(в
соответствии с разворотом плана)Слайд 32Высоту оконного проема мы измеряем на ребре перспективного изображения, расположенного
в картине.
Ширину окна определяем по линиям связи с построенного
плана здания●
●
●
●
а
а
Н
Н
ФАСАД
(ортогональная проекция)
ФАСАД
(в соответствии с разворотом плана)