Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реологические свойства биологических тканей
Содержание
- 1. Реологические свойства биологических тканей
- 2. План лекцииМеханические модели, реологическое уравнение абсолютно упругих,
- 3. Деформация это изменение формы и размеров тела под действием внешних сил либо температурыхарактеризуется механическим напряжением (σ)
- 4. В твердых телах деформацию называют:упругой, если после
- 5. Виды деформацииРАСТЯЖЕНИЕ (СЖАТИЕ)СДВИГИЗГИБКРУЧЕНИЕ
- 6. РАСТЯЖЕНИЕ (СЖАТИЕ)σ = F/Sσ – механическое напряжение
- 7. Закон ГукаПри небольшой величине относительной деформации связь
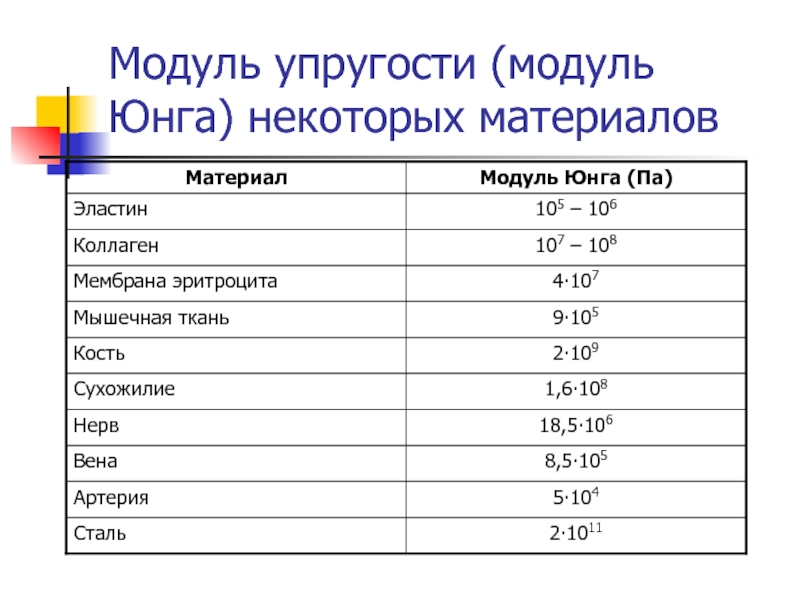
- 8. Модуль упругости (модуль Юнга) некоторых материалов
- 9. Зависимость напряжения от деформации (диаграмма растяжения)σσпр.АВСDООА –упругая деформация, АВ – пластическая деформация, ВС – текучесть
- 10. Реологические модели Модель упругого тела (пружина)
- 11. Модель вязкого тела (поршень) Поршень с отверстиями, движется
- 12. Модель Максвелла (упруго-вязкий элемент) Напряжение в
- 13. В момент времени t=0 пружина растягивается, затем
- 14. Скорость общей деформации равна:С помощью модели Максвелла можно моделировать следующие процессы:
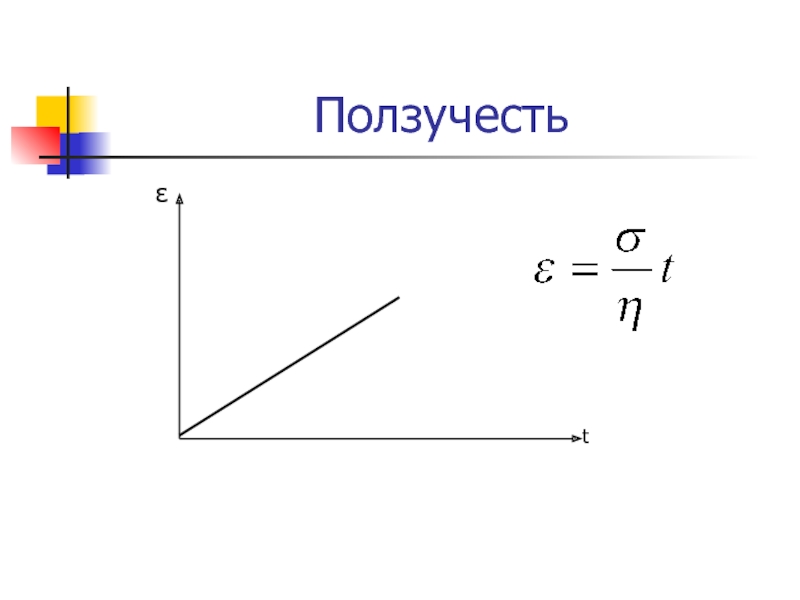
- 15. Ползучестьσ = const, dσ/dt = 0, dε/dt =σ/η
- 16. Ползучестьεt
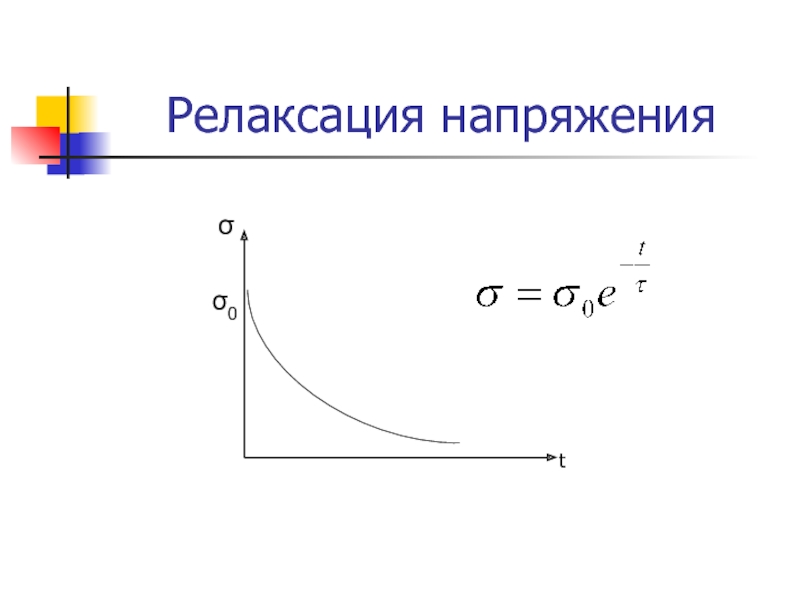
- 17. илигдеРелаксация напряжения в материалеε=const; dε/dt =0
- 18. Релаксация напряженияtσ σ0
- 19. Модель Кельвина–ФойгтаУдлинение одинаково для обоих элементов.илиσ = σупр + σвяз
- 20. В начальный момент времени деформация равна нулю,
- 21. В рамках модели Кельвина–Фойгта деформация экспоненциально возрастает со временем. При снятии нагрузки деформация экспоненциально убывает.
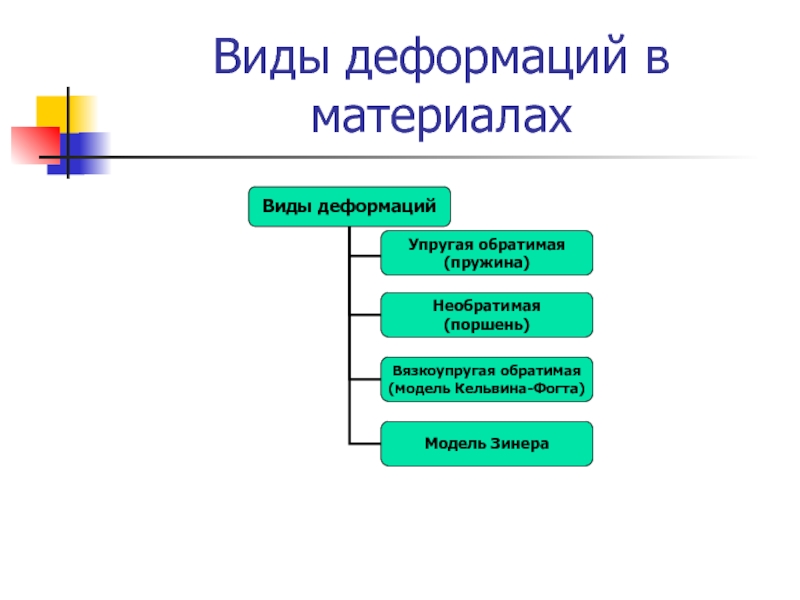
- 22. Виды деформаций в материалах
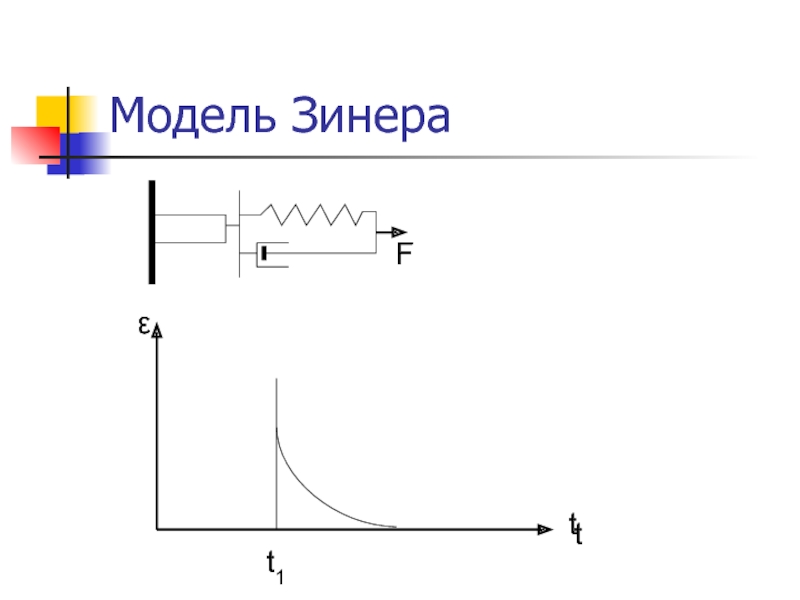
- 23. Модель ЗинераFε
- 24. Прочность – способность тел выдерживать без разрушения
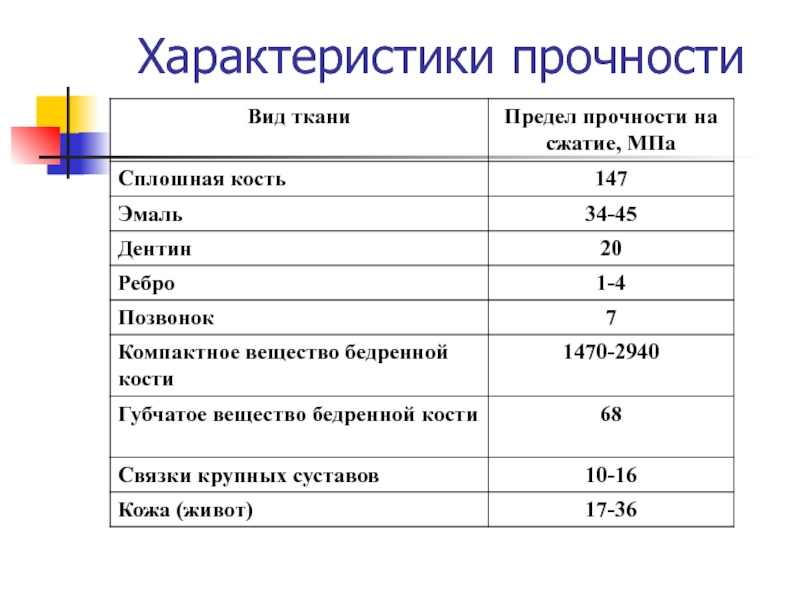
- 25. Характеристики прочности
- 26. Разрушение – макроскопическое нарушение целостности материала в
- 27. МЕХАНИЧЕСКИЕ СВОЙСТВА БИОЛОГИЧЕСКИХ ТКАНЕЙ.Большинство тканей являются анизотропными
- 28. Типы тканей Костная ткань –основной материал опорно-двигательного аппарата. КожаМышечная тканьСосудистая ткань
- 29. Костная ткань Состав:Гидроксилапатит. Коллаген (волокнистый, высокоэластичный белок).
- 30. Примерный вид кривой ползучести компактной костной тканиОА-
- 31. Механические свойства костной тканиОпределяются:возрастом;заболеваниями; условиями роста. Плотность
- 32. Функции кожи:поддержание гомеостаза участие в процессе терморегуляциирегуляция
- 33. Состав кожи Коллаген (75% сухой массы),Эластин (4%)
- 34. Мышечная ткань состоит из:КоллагенаЭластина Мышцы бывают:скелетные (сердечная)гладкие (кишечник)Плотность мышц 1100кг/м3; Е= 105 МПа.Поведение описывается моделью Максвелла
- 35. Скелетная мышца представляет собой вязкоупругий материал (модель
- 36. Режим сокращения мышц:Изометрический (длина мышцы не изменяется,
- 37. СОСУДИСТАЯ ТКАНЬМеханические свойства кровеносных сосудов определяются свойствами
- 38. Рассмотрим деформацию сосуда, длиной L и толщиной
- 39. Модели кровообращенияМодель Франка (упругий резервуар)Электрическая модельМодель с распределенными параметрами
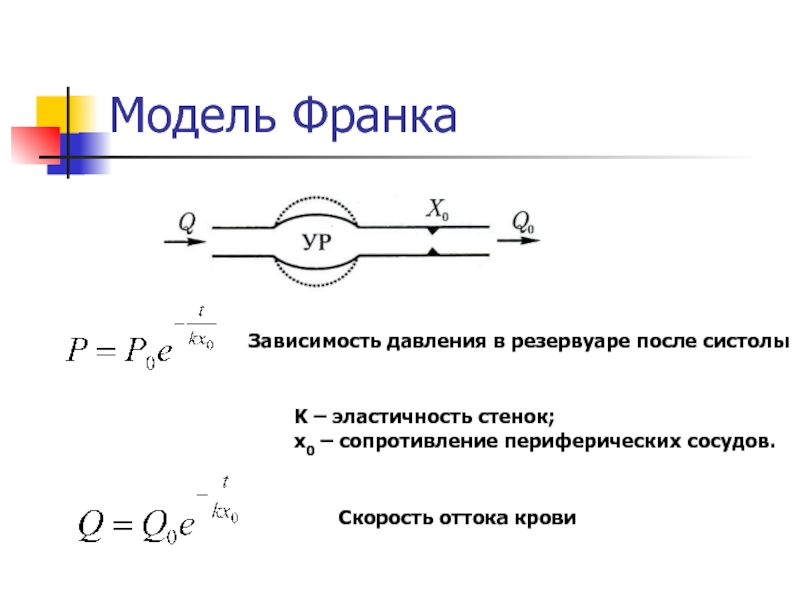
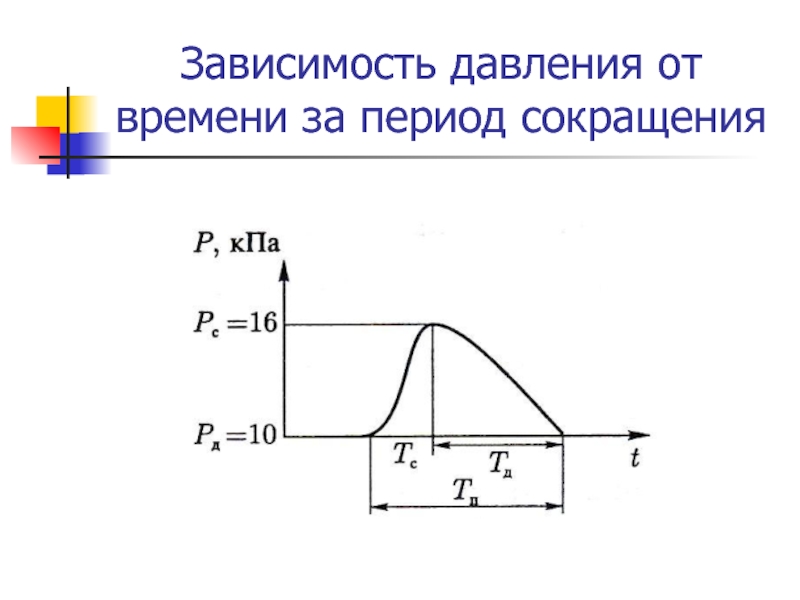
- 40. Модель ФранкаK – эластичность стенок; х0 –
- 41. Зависимость давления от времени за период сокращения
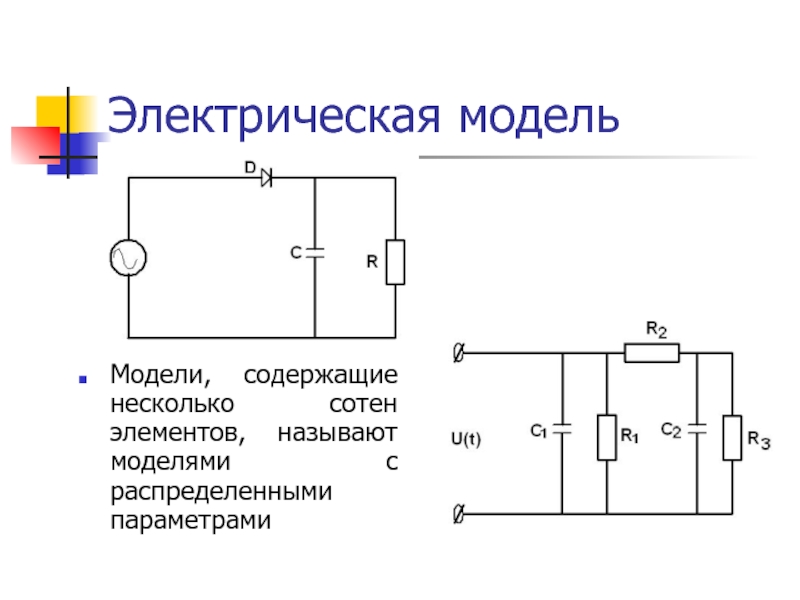
- 42. Электрическая модельМодели, содержащие несколько сотен элементов, называют моделями с распределенными параметрами
- 43. Пульсовая волнауравнение гармонической пульсовой волныЕ – модуль
- 44. БЛАГОДАРЮ ЗА ВНИМАНИЕ
- 45. Уважаемые старосты!Вы сдали списки отсутствующих?
- 46. Скачать презентанцию
План лекцииМеханические модели, реологическое уравнение абсолютно упругих, вязких и пластических тел.Упруго вязкие системы. Механическая модель Максвелла.Вязкоупругие системы. Механическая модель Кельвина–Фойгта.Общая характеристика реологических свойств мягких и твердых биологических тканей.
Слайды и текст этой презентации
Слайд 2План лекции
Механические модели, реологическое уравнение абсолютно упругих, вязких и пластических
тел.
характеристика реологических свойств мягких и твердых биологических тканей.
Слайд 3Деформация
это изменение формы и размеров тела под действием внешних
сил либо температуры
характеризуется механическим напряжением (σ)
Слайд 4В твердых телах деформацию называют:
упругой, если после прекращения действия сил
она исчезает
пластической, если после прекращения действия сил она сохраняется
упругопластической, если
после прекращения действия сил, происходит неполное ее исчезновение
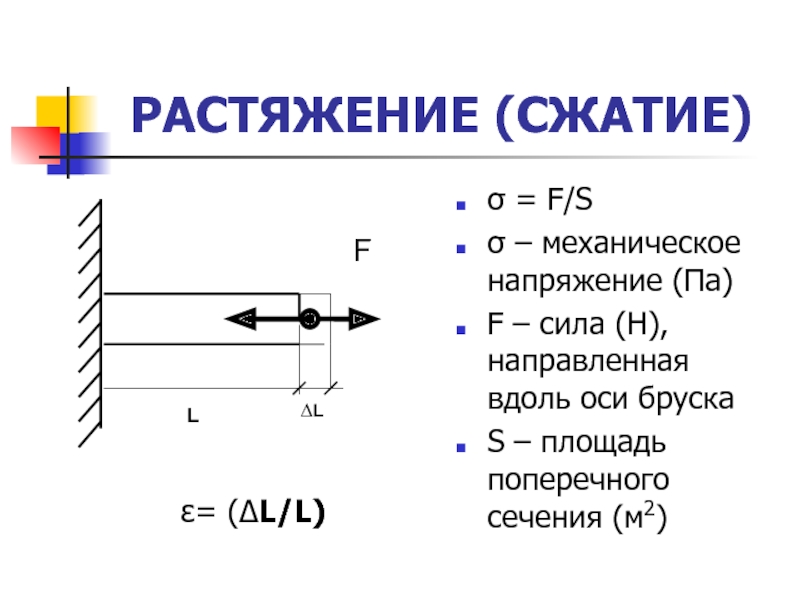
Слайд 6РАСТЯЖЕНИЕ (СЖАТИЕ)
σ = F/S
σ – механическое напряжение (Па)
F – сила
(Н), направленная вдоль оси бруска
S – площадь поперечного сечения (м2)
ε=
(∆L/L)
Слайд 7Закон Гука
При небольшой величине относительной деформации связь между механическим напряжением
и деформацией выражается законом Гука:σ = Еε
При упругой деформации напряжение
прямо пропорционально величине деформацииЕ – модуль Юнга (модуль продольной упругости, Па), численно равен напряжению, увеличивающему длину образца в два раза
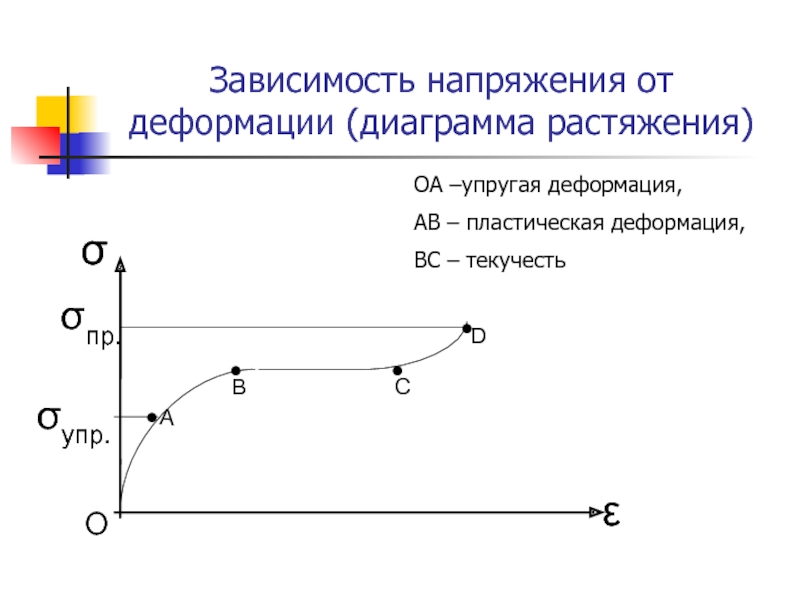
Слайд 9Зависимость напряжения от деформации (диаграмма растяжения)
σ
σпр.
А
В
С
D
О
ОА –упругая деформация,
АВ –
пластическая деформация,
ВС – текучесть
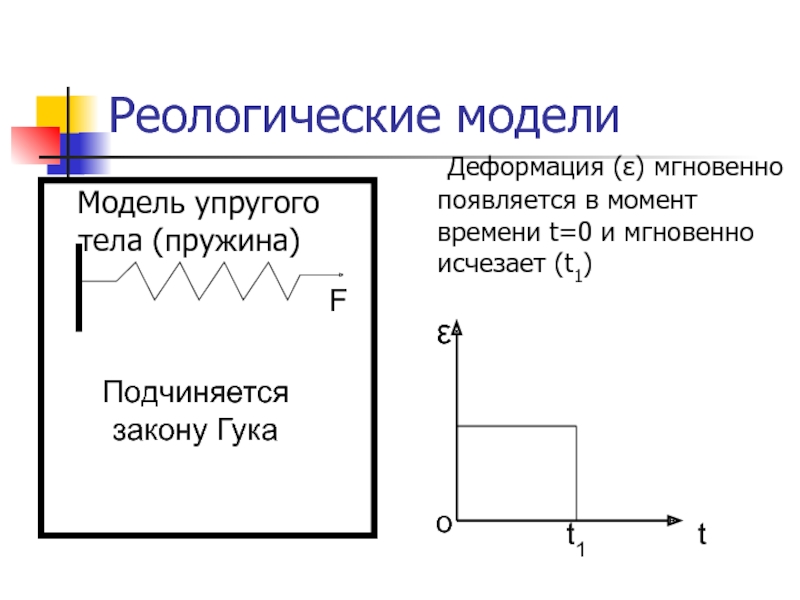
Слайд 10Реологические модели
Модель упругого тела (пружина)
Деформация (ε)
мгновенно появляется в момент времени t=0 и мгновенно исчезает (t1)
Подчиняется
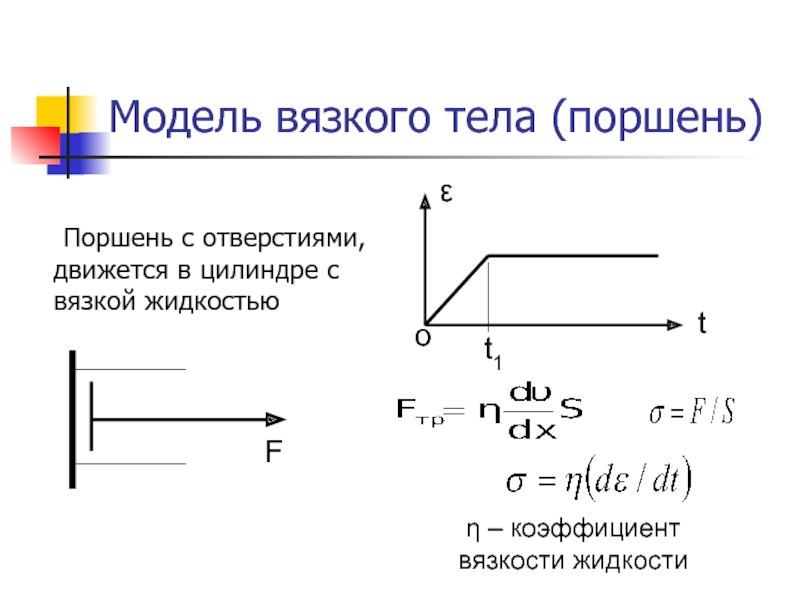
закону Гука
Слайд 11Модель вязкого тела (поршень)
Поршень с отверстиями, движется в цилиндре с
вязкой жидкостью
η – коэффициент вязкости жидкости
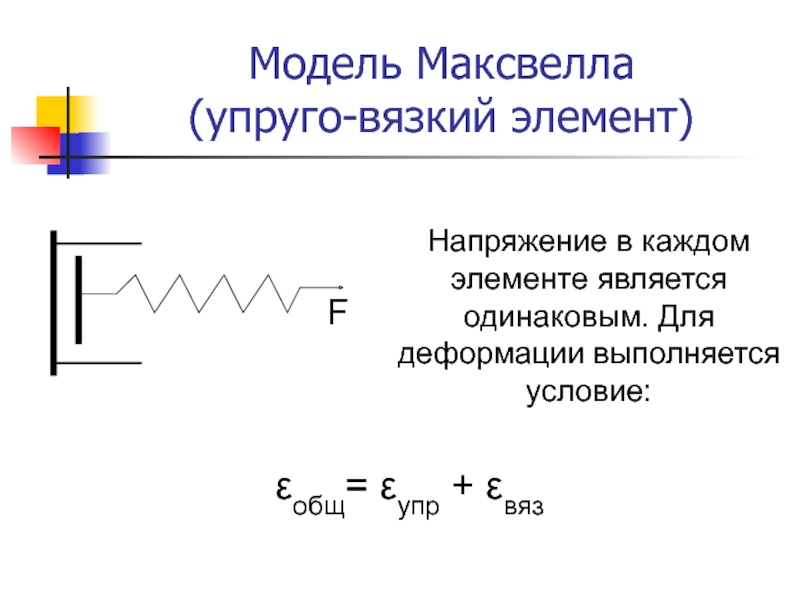
Слайд 12Модель Максвелла
(упруго-вязкий элемент)
Напряжение в каждом элементе является одинаковым.
Для деформации выполняется условие:
εобщ= εупр + εвяз
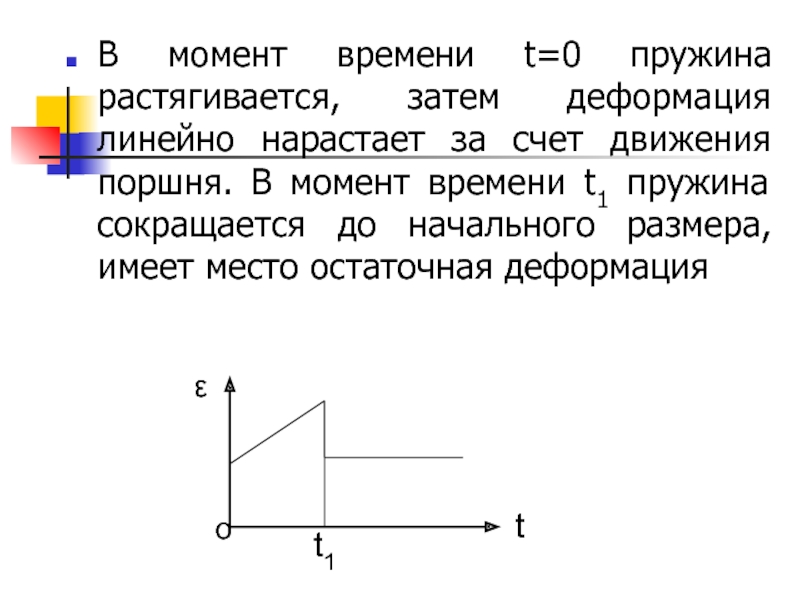
Слайд 13В момент времени t=0 пружина растягивается, затем деформация линейно нарастает
за счет движения поршня. В момент времени t1 пружина сокращается
до начального размера, имеет место остаточная деформация
Слайд 14Скорость общей деформации равна:
С помощью модели Максвелла можно моделировать следующие
процессы:
Слайд 20В начальный момент времени деформация равна нулю, а в момент
времени t равна ε
получим
Потенцируя данное выражение получим
или
Слайд 21В рамках модели Кельвина–Фойгта деформация экспоненциально возрастает со временем.
При
снятии нагрузки деформация экспоненциально убывает.
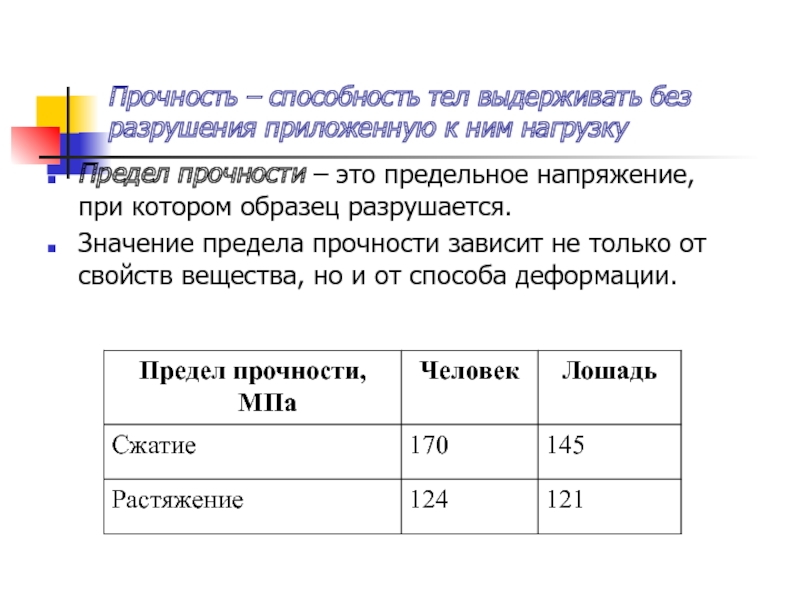
Слайд 24Прочность – способность тел выдерживать без разрушения приложенную к ним
нагрузку
Предел прочности – это предельное напряжение, при котором образец разрушается.
Значение предела прочности зависит не только от свойств вещества, но и от способа деформации.
Слайд 26Разрушение – макроскопическое нарушение целостности материала в результате механических (или
иных) воздействий.
Характер разрушения зависит от:
свойств материала;
состояния вещества (структуры);
температуры;
влажности;
свойств объекта (размеры,
форма, качество поверхности);динамики силового воздействия.
Слайд 27МЕХАНИЧЕСКИЕ СВОЙСТВА БИОЛОГИЧЕСКИХ ТКАНЕЙ.
Большинство тканей являются анизотропными композитными материалами, образованными
объемным сочетанием химически разнородных компонентов. Состав каждого типа тканей также
зависит от ее функций.
Слайд 28Типы тканей
Костная ткань –основной материал опорно-двигательного аппарата.
Кожа
Мышечная ткань
Сосудистая ткань
Слайд 29Костная ткань
Состав:
Гидроксилапатит.
Коллаген (волокнистый, высокоэластичный белок). Кристаллики гидроксилапатита расположены между
коллагеновыми волокнами (фибриллами).
Способность кости к упругой деформации реализуется за
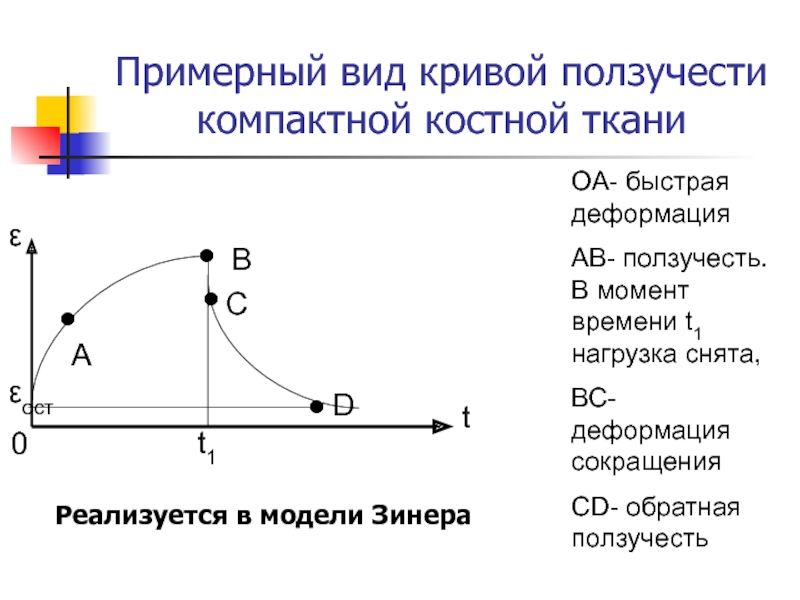
счет минерального вещества, а ползучесть – за счет коллагена.
Слайд 30Примерный вид кривой ползучести компактной костной ткани
ОА- быстрая деформация
АВ- ползучесть.
В момент времени t1 нагрузка снята,
ВС- деформация сокращения
СD- обратная
ползучесть●
●
εост
Реализуется в модели Зинера
Слайд 31Механические свойства костной ткани
Определяются:
возрастом;
заболеваниями;
условиями роста.
Плотность – 2400 кг/м3.
Е = 1010 Па, предел прочности
σпр = 100 МПа,
относительная деформация – 1%. Бедренная кость в продольном направлении
выдерживает нагрузку 45000 Н, а при изгибе – 2500 Н.
Запас механической прочности:
бедренная и берцовая кости выдерживают нагрузки в
25 - 30 раз больше веса нормального человека
Слайд 32Функции кожи:
поддержание гомеостаза
участие в процессе терморегуляции
регуляция общего обмена веществ
секреторная
функция
защита от внешних воздействий (механических, физических, химических).
Кожа состоит из:
эпидермиса
дермы,
подкожной клетчатки.
Слайд 33Состав кожи
Коллаген (75% сухой массы),
Эластин (4%)
Матрица
Кожа вязкоупругий
материал с высокоэластичными свойствами, обладающий акустической анизотропией.
Механические характеристики:
коллаген – Е= 10-100 МПа,
σпр = 100 МПа;
эластин - Е= 0,5 МПа,
σпр = 5 МПа
Эластин растягивается до 200 – 300%, коллаген до 10%.
Слайд 34Мышечная ткань состоит из:
Коллагена
Эластина
Мышцы бывают:
скелетные (сердечная)
гладкие (кишечник)
Плотность мышц 1100кг/м3;
Е= 105 МПа.
Поведение описывается моделью Максвелла
Слайд 35Скелетная мышца
представляет собой вязкоупругий материал (модель Зинера). Для нее характерна
релаксация напряжения. Модуль упругости мышцы зависит от нагрузки и называется
эффективным или тангенциальным.
Слайд 36Режим сокращения мышц:
Изометрический (длина мышцы не изменяется, вся сила затрачивается
на совершение статической работы);
Изотонический (поддерживается постоянное напряжение мышцы).
Слайд 37СОСУДИСТАЯ ТКАНЬ
Механические свойства кровеносных сосудов определяются свойствами коллагена, эластина и
гладких мышечных волокон.
С удалением от сердца увеличивается доля гладких
мышечных волокон, в артериолах они являются основной составляющей сосудистой ткани. Стенки сосудов способны к значительным обратимым изменениям размера под действием деформирующей силы, обусловленной избыточным внутренним давлением.
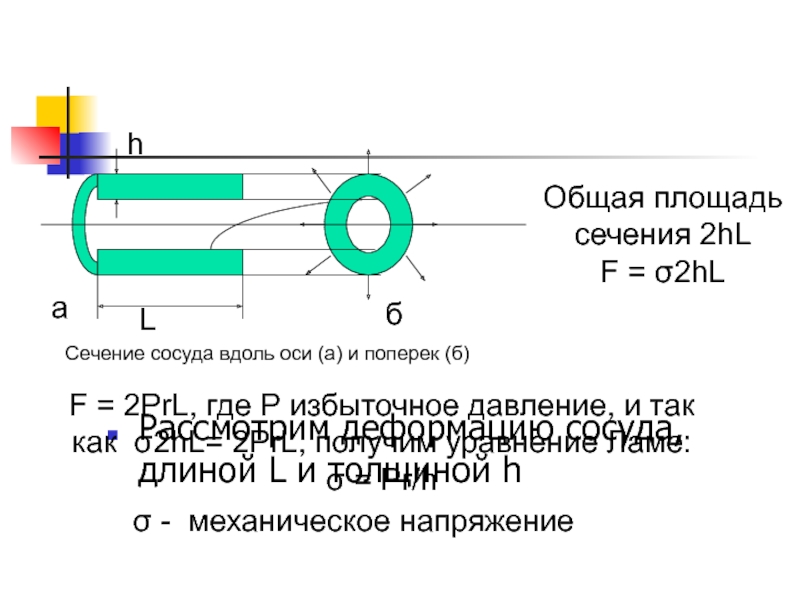
Слайд 38Рассмотрим деформацию сосуда, длиной L и толщиной h
h
Общая площадь сечения
2hL
F = σ2hL
F = 2PrL, где Р избыточное давление, и
так как σ2hL= 2PrL, получим уравнение Ламе:σ = Pr/h
σ - механическое напряжение
Слайд 39Модели кровообращения
Модель Франка (упругий резервуар)
Электрическая модель
Модель с распределенными параметрами
Слайд 40Модель Франка
K – эластичность стенок;
х0 – сопротивление периферических сосудов.
Зависимость
давления в резервуаре после систолы
Скорость оттока крови
Слайд 42Электрическая модель
Модели, содержащие несколько сотен элементов, называют моделями с распределенными
параметрами
Слайд 43Пульсовая волна
уравнение гармонической
пульсовой волны
Е – модуль упругости;
ρ –
плотность вещества;
h – толщина стенки сосуда;
d – диаметр сосуда.
Формула
Моенса–Кортевега
